一种TCN的改进模型及其在短期光伏功率区间预测的应用

宋绍剑　姜屹远　刘斌

摘 要：为了提高光伏功率预测的精度，提出了一种基于时序卷积网络（temporal convolutional network，TCN）的新型短期光伏功率区间预测模型。首先，采用深度残差收缩网络（deep residual shrinkage network，DRSN）的软阈值和注意力机制来改进TCN的残差模块以增强其对有用特征提取能力，并削弱冗余特征的不利影响；然后，利用樽海鞘群算法（slap swarm algorithm，SSA）对TCN的卷积层的卷积核大小和TCN层数等超参数进行自动寻优，以克服原TCN感受野不足的问题；接着，采用核密度估计（kernel density estimation，KDE）方法对所建改进TCN短期光伏功率预测模型的点预测结果进行误差分析，获得模型预测输出的区间。最后，通过对比仿真实验得到的结果表明，提出的SSA-DRSN-TCN模型的RMSE平均值为0.27，优于LSTM、GRU、CNN-LSTM和TCN等模型；而且，KDE方法能够在80%、90%和95%的置信度下准确描述光伏功率波动区间，验证了所提模型在提高光伏功率预测性能上的有效性。

关键词：光伏；短期功率预测；区间预测；时间卷积网络；深度残差收缩网络；樽海鞘群算法

中图分类号：TP183 文献标志码：A 文章编号：1001-3695（2023）10-028-3064-06

doi：10.19734/j.issn.1001-3695.2023.02.0066

Improved TCN model and its application in short-term

photovoltaic power interval prediction

Song Shaojian，Jiang Yiyuan，Liu Bin

（School of Electrical Engineering，Guangxi University，Nanning 530004，China）

Abstract：In order to improve the accuracy of PV power prediction，this paper proposed a new short-term PV power interval prediction model based on TCN.Firstly，the model used the soft threshold and attention mechanism of DRSN to modify the residual module of TCN so as to enhance its capability to extract useful features，and reduce the impact of redundant features.Then，it adopted the SSA to search the optimal hyper-parameters automatically，such as the convolutional kernel size and the number of TCN layers in the convolutional layer of the TCN，to overcome the drawback of the original TCN with insufficient receptive fields.Next，this paper applied the KDE to analyze the error of the point prediction results of the proposed improved TCN short-term PV power forecasting model to obtain its output interval.Finally，comparative simulation experiments show that the RMSE of the proposed SSA-DRSN-TCN model can reach 0.27，which is better than those of LSTM，GRU，CNN-LSTM and TCN，and the KDE method can accurately describe the PV power volatility intervals at 80%，90% and 95% confidence levels，the proposed model verifies the effectiveness in improving the performance of PV power prediction.

Key words：photovoltaic（PV）；short-term power forecasting；interval forecasting；temporal convolutional network；deep residual shrinkage network；slap swarm algorithm

0 引言

近些年來，太阳能光伏发电因其储量丰富、清洁环保等优点受到了世界多国的广泛关注［1］。然而，由于光伏发电输出的随机性、间歇性和波动性，大规模的光伏电源接入对电网的调度和安全稳定运行带来巨大的挑战。所以，准确的光伏功率预测是实现对光伏电源进行科学调度的关键［2，3］。

短期光伏功率预测一般是指1～3日内的短期功率预测，对电网实时调度具有重要的指导作用，也对系统的安全和稳定运行产生直接影响。目前，短期光伏功率预测方法主要有物理方法、统计方法和人工智能方法［4］。由于光伏功率受到辐照度、温度、湿度等多种复杂因素影响，传统的物理方法和统计方法难以准确地描述光伏发电系统内部的复杂特性。而人工智能方法能够利用人工神经网络良好的非线性映射能力，从历史数据中提取各种影响因素与输出功率之间的内在关系，因此，此类方法逐步成为光伏功率预测的主流方法［5］。其中，循环神经网络（recurrent neural network，RNN）的变体——长短期记忆网络（long short term memory，LSTM）［6］及其改进型，如门控循环单元（gate recurrent unit，GRU）［7］、双向LSTM网络（bi-directional LSTM，Bi-LSTM）［8］等，因其具有无限长度地保留序列信息的能力而被广泛应用于时间序列预测任务。尽管上述基于RNN架构及其变体的模型取得了较好的预测精度，但模型训练过程往往需要消耗大量的时间和计算内存，而且在网络训练过程中还常常面临梯度爆炸或梯度消失等问题。为此，2017年Bai等人［9］提出了时序卷积神经网络（temporal convolutional network，TCN），长输入序列可以在TCN中作为一个整体进行处理，能以更快的速度读取数据，因此具有较强的并行计算能力。此外，TCN的反向传播路径与序列的时间方向不同，这使得TCN避免了RNN中存在的梯度问题。鉴于以上优点，目前TCN模型已开始被应用到电力负荷预测［10］、风力发电功率预测［11］、风速预测［12］等时序预测问题。不过，TCN自身也存在着以下缺陷：a）数据中存在的次要冗余特征信息会干扰TCN的特征提取，进而影响最终的预测结果；b）TCN的感受野大小取决于其网络层数、卷积核大小等网络参数，它直接关系到模型的特征提取性能、预测精度和内存开销，如何选择合适的TCN超参数主要依赖人工试凑，导致效率低，适应性差。

此外，目前的光伏预测研究主要侧重于光伏输出功率的点预测，即对某个时刻的单点期望值进行预测［13］。由于受到预测模型本身误差的限制，点预测不能反映光伏功率预测的波动上下界，难以量化光伏功率预测结果的不确定性。而基于区间的不确定性预测能够描述光伏电源的变化范围、概率分布以及可能发生的场景，可以获得更为全面的预测信息，因而备受人们关注。区间预测方法主要分为参数方法和非参数方法［14］，在实际应用中误差分布的函数往往难以事先确定。非参数方法无须事先假设误差分布函数也能够较为准确地量化波动区间，因此是目前较为主流的区间预测方法。目前常用的非参数方法有分位數回归（quantile regression，QR）、Bootstrap等［15］，但这些已有的方法普遍存在计算过程复杂、计算量大的局限性。

综上所述，如何进一步提升光伏输出功率预测的精度，同时降低模型的计算代价仍有待进一步深入研究。为此，本文提出了一种基于改进TCN的光伏功率区间预测新方法。首先，将DRSN的注意力机制和软阈值机制引入TCN的残差连接模块，增强数据中的重要特征并抑制非重要特征的影响，降低冗余信息对网络学习效果的不利影响；其次，针对TCN的网络层数和超参数难以人工确定的问题，利用SSA良好的勘探与开发能力，通过自动寻优方法确定TCN的超参数，避免人工试凑的随机性；最后，在模型点预测结果的基础上，使用非参数方法中的KDE方法分别计算不同置信度下的模型预测输出区间上下界。与现有的方法相比，本文方法在预测精度上有显著提升，即便改进后的模型复杂度有所增加，额外的时间代价也在可接受范围内。

1 基于SSA优化的DRSN-TCN短期光伏功率点预测模型

为了削弱样本数据中的次要冗余特征对TCN特性提取过程造成的干扰，本文拟采用DRSN对TCN的残差模块进行改进，将注意力机制与软阈值机制结合，在计算各输入特征的权重后，使得TCN更加关注对光伏功率影响较大的重要特征，同时削弱影响微弱的次要特征；再采用SSA对网络参数进行自动寻优，以获得最适合的预测感受野；最后将改进后得到的网络用于建立短期光伏功率点预测模型。

1.1 DRSN-TCN模型

1.1.1 TCN结构

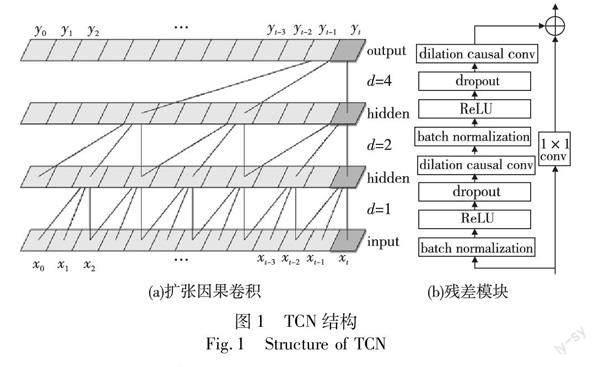
TCN是一种由因果卷积和扩张卷积组成的CNN结构，如图1（a）所示。与普通一维卷积相比，扩张因果卷积的主要特点是：

a）TCN采用了一种独特的因果卷积，保证了输入序列的因果关系，避免了未来数据的泄漏，同时还扩大了感受野。各隐层的整体感知和信息长度与输入序列相同，保证了序列作为一个整体对深度网络产生影响。

b）为了解决由于捕获信息而产生的线性叠加问题，TCN采用了一种扩张卷积算法。扩张卷积的卷积核与普通卷积不同，它是以间隔采样的方式读取数据，采用这种采样方式有助于让TCN在处理数据时获得更大的序列特征感受野，保存更多的历史信息。扩张卷积的第s个神经元的输出表示为

其中：代表卷积运算；l为卷积核大小；d为扩张系数；f（i）为卷积核中的第i个元素；xs-d·i是与卷积核对应相乘的元素。

c）引入残差模块来解决卷积退化导致的梯度消失问题。通过增加残差连接，可以直接跨层输入数据而不跳过中间链路。它的优点是避免了TCN在特征提取过程中丢失过多的信息，将因果卷积提取的特征数据相加得到最终的输出。残差模块主要是由两个扩张因果卷积、批归一化、dropout、ReLU激活函数等模块封装而成。另外，加入一个1×1的卷积来保持输出的尺度与输入的尺度相同，其结构如图1（b）所示。

图1中展示了卷积核大小为k=3时的扩张因果卷积图。其中，t时刻的输出yt由当前的输入以及之前的输入决定，即x0，x1，x2，…，xt，说明预测输出不受未来信息的影响，因此避免了信息泄露。此外，引入扩张系数d对卷积层的输入矩阵进行间隔采样，在第一隐层中，采样间隔率d=1，代表输入的每个点都采样；在第二隐层中，采样间隔率d=2，即每两个点取一次，忽略一个神经元。依此类推，在更高的层数使用的d呈指数型增长，从而能做到以较少的层数获得较大的感受野。正由于具有这些特点，长输入序列可以在TCN中作为一个整体进行处理，能以更快的速度读取数据。此外，TCN的反向传播路径与序列的时间方向不同，使得TCN避免了梯度爆炸和梯度消失的问题。但是TCN在处理大量数据时，由于计算能力有限，若对数据中的特征进行完全提取也会占用大量资源，并且次要特征及冗余特征会降低网络对重要特征信息的关注度，从而影响到模型最终预测的准确性。

1.1.2 DRSN结构

DRSN是残差网络的一种改进算法，它能够将注意力机制和软阈值机制结合，从而实现自主的滤波学习。相比于传统的小波阈值更为高效、准确，可以避免人为设定阈值的烦琐和盲目性，达到减少次要冗余特征对网络影响的目的［16］。因此，将用DRSN替换TCN基准网络中普通残差网络通过注意力机制获得合适的阈值，再通过软阈值机制降低网络内噪声波动的影响。图2（a）为TCN原来的普通残差网络结构，它由两个卷积层、两个批归一化层（BN）、两个ReLU激活函数和一个跨层恒等连接组成。其标志性特点是通过使用残差连接，避免了卷积退化。图2（b）为DRSN模块的结构。DRSN在原残差网络的基础上增加了软阈值（soft thresholding）机制和注意力机制（attention mechanism）。

软阈值机制是一种信号降噪方法，其原理是设定一个阈值，将绝对值小于阈值范围内的接近0的特征信号置为0，将其他特征信号也相对朝着0值收缩。软阈值机制的输出及其导数为

其中：x为输入值；f（x）为软阈值化后的输出；τ为阈值。可知该软阈值化函数的导数是0或者1，可以很好地防止梯度消失和梯度爆炸问题。由于阈值τ的取值起到了关键作用，若取值不当会影响DRSN的性能，所以需要采用注意力机制自动获取阈值，减少人工设置参数的不确定性。

在注意力模块部分，先对特征层中的绝对值进行全局均值池化（global average pooling，GAP）以减少FC输出层使用的权值数量，从而降低深度神经网络面临过拟合的可能性。随后将GAP得到的一维向量传递到全连接层（fully connected，FC），再由sigmoid函数缩放到（0，1）内，α表示缩放后得到的权值。将α与GAP输出的绝对值相乘得到阈值，保证得到的阈值为正数。这个过程可表示为

其中：τ为软阈值过程所需要的阈值；xp，q，r为特征层的输入。

经过DRSN的软阈值处理，能够在残差网络的基础上逐步减少数据中的冗余特征对网络的影响，减少TCN在评估期间的内存占用。注意力机制为阈值的选取提供了参考，避免了人工设定阈值时的盲目性和随机性。

1.1.3 DRSN-TCN组合模型设计

本节在TCN的特征输出层后加入DRSN模块，将TCN中的残差连接与注意力机制组合为软阈值滤波模块，其结构如图3所示。在TCN的多层扩张因果卷积之后，将特征层的信息经由注意力机制和软阈值化后，注意力机制增强了对关键特征的关注，软阈值机制减少了次要特征的内存占用，既能够有效节省计算资源，还可以提高预测结果的准确性。

1.2 基于SSA的DRSN-TCN模型优化

TCN的感受野大小主要由扩张因果卷积核大小l及扩张系数d决定。由于扩张系数d随着TCN的层数k呈指数型增长，所以确定卷积核大小l及层数k对TCN的感受野大小起到关键性作用。若这些参数设置得不合适，不仅会大大地增加计算时间，甚至还会产生较大的预测误差。因而，有必要根据具体TCN的超参数对TCN的感受野大小进行寻优。目前常见的一些优化算法，如粒子群算法［17］（particle swarm optimization，PSO）、遗传算法［18］（genetic algorithm，GA）等，虽然对网络参数优化有一定效果，但是大多数群智能优化算法存在结构复杂、搜索速度慢、易陷入局部最优等问题，为此本节选用了一种结构更为简单、搜索速度更快的SSA对卷积核大小、卷积层数等参数进行自动寻优。

1.2.1 SSA

SSA是由Mirjalili等人［19］提出的一种基于海洋生物樽海鞘群的觅食行为的智能群优化算法。海鞘种群分为领导者与追随者，在一个群体中，领导者个体用连续动作将追随者引导至一个更好的位置，而其余的海鞘被视为追随者，互相跟随，在领导者的带领下呈链状进行觅食行为。SSA的流程如图4所示，与其他基于群体智能的技术类似，樽海鞘的位置是在p维搜索空间中定义的，其中p是需要优化变量的个数，NSSA为樽海鞘总个数。因此，所有樽海鞘的位置都存储在一个名为X的二维矩阵中。假设在搜索空间中有一个名为F的食物源作為种群的目标，为了搜索食物源，领导者的位置按以下公式更新：

其中：x1j表示第一个樽海鞘（即领导者）在第j维的位置；Fj为食物在第j维的位置；ubj和lbj分别表示搜索范围的上界和下界；c1、c2、c3均为随机数。

从式（5）可以看出，领导者只负责更新与食物之间的位置，而控制参数是搜索过程中的重要参数，其定义如下：

其中：n和N分别代表当前迭代次数和最大迭代次数。c1能够平衡SSA的勘探和开发两种模式，即在搜索初期，领导者进行大范围勘探以确定食物的大致范围，随着迭代的进行，领导者逐渐缩小搜索步长，转为小范围内的开发模式，从而锁定食物的准确位置。这些特性使得SSA具有较高的搜索效率。系数c2、c3是0～1的随机数，用于增强随机性，提高搜索的多样性。

随着领导者的位置更新，追随者的位置按照如式（7）所示的规律更新。

其中：xij表示第i个樽海鞘在第j维的位置，由于是追随者，i≥2；t表示时间；v0为初始速度；a=（vfinal-v0）/t。由于迭代间隔为1，初始速度可以视为0，则SSA每次迭代后都能保留最优解，根据食物的位置更新领导者的位置，跟随者依据前面的樽海鞘更新自己的位置，这种特性避免了SSA陷入局部最优，有利于在未知空间中进行搜索。

1.2.2 基于SSA的TCN改进模型

由于决定TCN感受野大小的超参数之间的关系复杂，需要SSA的自适应特性来避免陷入局部最小问题，并能找到全局最优的解决方案。图5给出了SSA-DRSN-TCN 模型的原理框图。该模型所需优化的参数包括TCN卷积核大小l和TCN层数k，其维度为2。经过SSA的多次迭代搜索后得到最优适应度所对应的TCN参数，再将其应用于基于DRSN-TCN的短期光伏功率预测模型中以得到更为精确的光伏功率预测结果。

2 基于KDE方法的短期光伏功率区间预测

由于光伏预测模型的输入通常仅选取影响光伏功率输出的主导因素，模型预测结果与真实值之间难免存在一定的误差，普通的点预测结果难以反映这种不确定性。基于区间的不确定性预测能够描述光伏功率的波动范围、误差概率分布以及可能发生的场景，可以获得更为全面的预测信息，是实际工程中的重要指标。由于受实际辐照度、温湿度等影响因素的随机性影响，模型预测结果的误差分布规律及参数难以事先假定，所以基于参数化的区间估计方法难以奏效。为此，本章将介绍非参数估计方法KDE的实现原理及其核函数和带宽的确定方法。

2.1 基于KDE方法估计置信区间

KDE方法基于大量的历史数据，采用核函数拟合出光伏功率预测误差的概率分布函数，主要步骤如下：a）分析DRSN-TCN模型预测误差百分比的概率分布；b）基于KDE-PDF方法估计预测区间，描述点预测概率分布的可能变化；c）对估计的功率值进行PICP检验，即功率值与实际功率的覆盖率，以判断所提KDE方法的有效性。

其中：K（·）表示核函数；fK（x）为K在x处的概率密度函数；m为总样本数；h为采样带宽；xi为第i个样本的值。核密度函数K（·）和采样带宽h是决定核密度估计结果的关键因素。

2.1.1 核函数的选取

将式（11）代入式（10）中即可得到样本分布下的概率密度函数。

2.1.2 采样带宽h的确定

在核函数确定之后，高斯核的带宽h不同会导致最后的拟合结果差别很大，因此选择合适的h对KDE很关键。给定样本容量Ns，若h较大，选取的点较多，可以减小方差，但不符合h→0的要求；若h太小，用于计算的数据太少会导致方差很大。常用的方法有网格搜索方法（Gridsearch）、Silverman经验法则等。其中Silverman经验法则是以平均积分平方误差（mean integrated squared error，MISE）为指标来衡量h的优劣。MISE的定义为

其中：c为常数，由正态分布可假设c=1.05×std（x），std（x）为标准差。Silverman经验法则相比Gridsearch方法计算更简单，但是当核密度不接近正态分布时可能会产生泛化极差的估计，此时Gridsearch方法将有更好的拟合效果。

2.2 光伏功率的区间预测方法

在确定了核函数和带宽后，根据概率密度函数采用积分法得到累积分布函数。在置信度1-α下，由式（14）（15）可得到t时刻下的预测区间上界Pup，t和下界Plow，t为

xu与xl分别为概率α1（1-α/2）和α2（α/2）所对应的分位数，其中F（xu）=α1，F（xl）=α2。由此可求出不同置信度下的预测区间。

3 算例分析

为了验证本文方法的有效性，选用澳大利亚的DKASC数据集中Trina 1B电站2020年光伏输出功率及天气数据［20］，采样间隔为30 min，共17 568个数据点。取1月1日至11月30日的数据为训练集，12月1日至12月25日的数据为验证集，12月26日至12月31日的数据为测试集。

为了降低模型复杂度、增强模型普适性，首先采用Pearson相关分析法分析影响该光伏电站功率输出的因素，最终选取辐照度、温度、湿度作为光伏功率预测模型的输入变量；其次，对采样频率为30 min的历史数据进行异常值剔除和缺失值的插值填补；由于输入变量与光伏功率量纲不同，为了加快模型收敛速度、减小预测误差，对光伏输出功率数据和天气数据进行归一化处理，将其缩放到［0，1］内。本文仿真实验的软硬件环境如下：处理器为Intel Core TM i5-9400F CPU@2.90 GHz，16 GB RAM，无GPU卡，Windows 10操作系统。所有仿真结果均在基于TensorFlow 2.1.0环境的Python 3.7.1完成。

3.1 评价指标选取

为了量化预测模型的精度，首先采用平均绝对误差（mean absolute error，MAE）、均方根误差（root mean square error，RMSE）和確定性系数（R2）作为评价光伏输出功率点预测精度的评价指标；其次，对于区间预测的结果，采用区间覆盖率（prediction intervals coverage probability，PICP）、预测区间平均宽度（prediction interval normalized average width，PINAW）和温克勒评分（Winkler score，WS）作为评价指标［21］。

3.2 光伏功率点预测结果及对比分析

为了验证本文DRSN-TCN模型的优越性，分别建立了LSTM、GRU、CNN-LSTM、TCN等当前主流模型作为对照模型。此外，为了验证SSA的优化性能，将对比原始模型、PSO算法优化模型和SSA优化模型的寻优效果。在实验过程中，为了保证对比实验的公平性，本文各种模型的epoch均设置为100，batch size设置为64，学习率设置为0.001，模型优化器选用Adam，种群数设置为20、迭代次数设置为50，损失函数定义为MAE，各模型训练时的损失函数曲线如图6所示。经过训练后，各模型在2020年12月26—31日的预测结果对比如图7所示。由图7可以看出，LSTM在几种模型中性能较差，与真实值偏差较大；GRU相比LSTM模型获得相对更高的准确度，CNN-LSTM模型的性能相比前两者均有显著提高，但仍落后于TCN模型，说明本文的DRSN-TCN具有较好的非线性拟合特性，预测效果最好。

为了更全面地检验DRSN-TCN模型性能，将它与LSTM、GRU、CNN-LSTM以及TCN的性能进行对比，结果如表1所示。其中，RMSE和MAE主要衡量预测误差性能，R2表示模型的拟合程度，time代表模型的训练时间。从表1可以看到，DRSN-TCN模型的预测误差最小，在所有模型中具有更好的非线性拟合特性，预测精度有着较大提升，尽管DRSN-TCN的复杂度稍有增加，但与原TCN相比，增加的时间开销很小。

为了展现SSA对DRSN-TCN模型超参数优化的效果，将其分别与优化前模型、PSO优化模型和鲸鱼优化（WOA）模型的结果进行了对比，结果如表2所示。从表2可以看出，SSA和PSO均能对原始模型起到优化效果，且SSA的效果较为显著；同时SSA相比PSO和WOA能更快地达到最优值，具有更出色的收敛速度。

3.3 光伏功率区间预测结果及对比分析

本节采用KDE方法在验证集上对SSA-DRSN-TCN模型的预测误差分布进行分析，分别采用Gridsearch方法和Silverman经验法则得到不同的采样带宽 ，经过Gaussian核函数拟合得到概率密度函数（probability density function，PDF），如图8所示，可以看出Gridsearch方法对于PDF有着更好的拟合特性。其次，将PDF积分得到误差密度积分函数（cumulative density function，CDF），如图9所示。最后在CDF上寻得各置信度下的置信区间，采用不同置信度下的区间偏差在测试集的点预测结果中进行区间预测。为了验证KDE方法的区间估计有效性，采用Bootstrap方法与之进行对比，所得到的区间预测结果如图10所示。

在表3中给出了三种方法在80%、90%、95%置信度下的PICP、PINAW、WS。由表3可知，在三种置信度水平下KDE方法的PICP都比Bootstrap方法优秀，意味着具有较高的可靠性，KDE（Gridsearch）的PINAW与Bootstrap相近，而KDE（Silverman）的锐度与两者相比有所欠缺。由于可靠性与锐度之间存在的矛盾，为了平衡两者，引入WS指标进行综合评价。可见Bootstrap方法在80%置信度下出现了较大的误差，且KDE方法在三种置信度水平下始终具有较为优秀的可靠性与锐度，其中Silverman方法综合效果最佳。

由综合点预测和区间预测结果可知，本文的DRSN-TCN光伏功率预测模型对光伏功率点预测有较高的精度，KDE方法能准确地描述误差分布，验证了本文方法的有效性和实用性。

4 结束语

针对TCN在光伏功率预测的过程中，冗余特征对计算资源的过多占用，以及TCN感受野变化对预测精度的影响，本文提出一种SSA优化的DRSN-TCN短期光伏功率区间预测模型。首先用DRSN对TCN模型的残差模块进行改进，并利用SSA对网络的关键参数（即卷积核大小、TCN层数）进行优化；其次采用优化好的模型进行光伏功率点预测；最后在点预测的结果上采用KDE方法进行概率密度分析，得到累积误差函数后计算出预测区间。经过对比研究，得到的主要结论如下：

a）本文的DRSN-TCN模型能够利用DRSN的注意力机制及软阈值机制使TCN更好地提取数据中的关键特征，使模型拥有更大的感受野，减少冗余特征的计算资源占用。与LSTM、GRU、CNN-LSTM和TCN等模型相比，具有更高的预测精度。

b）SSA可以对TCN的超参数进行寻优，从而确立较大的感受野。相比PSO、WOA等优化方法，SSA具有较快的寻优速度，能够更好地避免陷入局部最优问题。

c）在区间预测中，KDE方法无须事先假设模型的分布参数，具有计算简单、灵活、出色的准确性和锐度，能够涵盖更多的信息，有利于作出决策，更符合实际工程中的需要。

本文仅在连续数据的基础上进行预测，在以后的工作中可以对数据进行天气、季节聚类以取得更好的预测效果。除了光伏功率预测之外，DRSN-TCN也适用于电力负荷预测、道路交通流量预测等其他多输入时间序列预测任务，具有广阔的应用前景。

参考文献：

［1］Takilalte A，Harrouni S，Yaiche M R，et al.New approach to estimate 5-min global solar irradiation data on tilted planes from horizontal measurement［J］.Renewable Energy，2020，145（1）：2477-2488.

［2］Huang Xiaoqiao，Li Qiong，Tai Yonghang，et al.Time series forecasting for hourly photovoltaic power using conditional generative adversarial network and Bi-LSTM ［J］.Energy，2022，246（5）：123403.

［3］Akhter M N，Mekhilef S，Mokhlis H，et al.A hybrid deep learning method for an hour ahead power output forecasting of three different photovoltaic systems ［J］.Applied Energy，2022，307（2）：118185.

［4］Ahmed R，Sreeram V，Mishra Y，et al.A review and evaluation of the state-of-the-art in PV solar power forecasting：techniques and optimization［J］.Renewable and Sustainable Energy Reviews，2020，124（5）：109792.

［5］赖昌伟，黎静华，陈博，等.光伏发电出力预测技术研究综述 ［J］.电工技术学报，2019，34（6）：1201-1217.（Lai Changwei，Li Jinghua，Chen Bo，et al.Review of photovoltaic power output prediction technology［J］.Trans of China Electrotechnical Society，2019，34（6）：1201-1217.）

［6］宋紹剑，李博涵.基于LSTM网络的光伏发电功率短期预测方法的研究 ［J］.可再生能源，2021，39（5）：594-602.（Song Shaojian，Li Bohan.Short-term forecasting method of photovoltaic power based on LSTM ［J］.Renewable Energy Resources，2021，39（5）：594-602.）

［7］姚程文，杨苹，刘泽健.基于CNN-GRU混合神经网络的负荷预测方法 ［J］.电网技术，2020，44（9）：3416-3423.（Yao Chengwen，Yang Ping，Liu Zejian.Load forecasting method based on CNN-GRU hybrid neural network ［J］.Power System Technology，2020，44（9）：3416-3423.）

［8］He Yanlin，Chen Lei，Gao Yanlu，et al.Novel double-layer bidirectio-nal LSTM network with improved attention mechanism for predicting energy consumption ［J］.ISA Trans，2022，127（8）：350-360.

［9］Bai Shaojie，Kolter J Z，Koltun V.An empirical evaluation of generic convolutional and recurrent networks for sequence modeling ［EB/OL］.（2018-04-19）.https：//arxiv.org/pdf/1803.01271.pdf.

［10］Bian Haihong，Wang Qian，Xu Guozheng，et al.Research on short-term load forecasting based on accumulated temperature effect and improved temporal convolutional network ［J］.Energy Reports，2022，8（Suppl 5）：1482-1491.

［11］Zha Wenting，Liu Jie，Li Yalong，et al.Ultra-short-term power forecast method for the wind farm based on feature selection and temporal convolution network ［J］.ISA Trans，2022，129（10）：405-414.

［12］Li Huang，Jiang Zhejuan，Shi Ziyi，et al.Wind-speed prediction model based on variational mode decomposition，temporal convolutional network，and sequential triplet loss ［J］.Sustainable Energy Techno-logies and Assessments，2022，52（8）：101980.

［13］黎静华，骆怡辰，杨舒惠，等.可再生能源电力不确定性预测方法综述 ［J］.高电压技术，2021，47（4）：1144-1155.（Li Jinghua，Luo Yichen，Yang Shuhui，et al.Review of uncertainty forecasting methods for renewable energy power ［J］.High Voltage Engineering，2021，47（4）：1144-1155.）

［14］Pan Cheng，Tan Jie，Feng Dandan.Prediction intervals estimation of solar generation based on gated recurrent unit and kernel density estimation［J］.Neurocomputing，2021，453（9）：552-562.

［15］Liu Luyao，Zhao Yi，Chang Dongliang，et al.Prediction of short-term PV power output and uncertainty analysis［J］.Applied Energy，2018，228（10）：700-711.

［16］Zhao Minghang，Zhong Shisheng，Fu Xuyun，et al.Deep residual shrinkage networks for fault diagnosis［J］.IEEE Trans on Industrial Informatics，2019，16（7）：4681-4690.

［17］Zheng Jianqin，Zhang Haoran，Dai Yuanhao，et al.Time series prediction for output of multi-region solar power plants［J］.Applied Energy，2020，257（1）：114001.

［18］程港，林小峰，宋绍剑，等.基于 PCA-GA-ELM 的光伏發电功率预测研究［J］.可再生能源，2019，37（10）：1440-1447.（Cheng Gang，Lin Xiaofeng，Song Shaojian，et al.Research on photovoltaic power generation prediction based on PCA-GA-ELM［J］.Renewable Energy Resources，2019，37（10）：1440-1447.）

［19］Mirjalili S，Gandomi A H，Mirjalili S Z，et al.Salp swarm algorithm：a bio-inspired optimizer for engineering design problems［J］.Advances in Engineering Software，2017，114（12）：163-191.

［20］DKASC.Trina 10.5kW，mono-Si［DB/OL］.https：//dkasolarcentre.com.au/source/alice-springs/dka-m9-b-phase.

［21］Van der Meer D W，Widén J，Munkhammar J.Review on probabilistic forecasting of photovoltaic power production and electricity consumption［J］.Renewable and Sustainable Energy Reviews，2018，81（1）：1484-1512.

收稿日期：2023-02-10；修回日期：2023-04-03基金项目：国家自然科学基金资助项目（61863003）；广西自然科学基金资助项目（2016GXNSFAA380327）

作者简介：宋绍剑（1970-），男，广西象州人，教授，硕导，硕士，CCF会员，主要研究方向为机器学习、人工智能、新能源变换与控制（sjsong03@163.com）；姜屹远（1998-），男，云南曲靖人，硕士研究生，主要研究方向为机器学习；刘斌（1982-），男，湖南会同人，副教授，博导，博士，主要研究方向为新能源变换与控制、电力电子技术．