引入动态分化和邻域诱导机制的双蚁群优化算法

禹博文　游晓明　刘升

摘 要：为提高传统蚁群算法在解决旅行商问题时的优化效果，提出了一种引入动态分化和邻域诱导机制的双蚁群优化算法。该算法首先引入混沌随机策略，在算法初始化阶段改变原始的贪心策略，使初始信息素混沌分布，以保持种群的多样性，从而提高解的精度；其次，将蚁群分为孤立蚁群与正常蚁群，两组蚂蚁分别在当前最优路径与离群路径附近搜索；在种群间采取诱导机制，正常蚁负责搜索最优路径，孤立蚁混沌随机释放信息素，将正常蚁群诱导至新的路径邻域，从而有效地平衡收敛速度与解的多样性之间的矛盾。通过对不同规模的旅行商问题仿真结果的比较，验证了所提算法的有效性。

关键词：旅行商问题； 蚁群优化； 动态分化策略； 混沌随机； 诱导策略

中图分类号：TP18 文献标志码：A 文章编号：1001-3695（2023）10-018-3000-07

doi：10.19734/j.issn.1001-3695.2023.02.0060

Dual-ant colony optimization algorithm with dynamic differentiation and neighborhood induction mechanism

Yu Bowena， You Xiaominga， Liu Shengb

（a.School of Electronic & Electrical Engineering， b.School of Management， Shanghai University of Engineering Science， Shanghai 201620， China）

Abstract：In order to improve the optimization effect of traditional ant colony algorithm in solving traveling salesman problem， this paper developed a dual-ant colony optimization algorithm with dynamic differentiation and neighborhood induction mechanism. Firstly， the algorithm introduced chaotic random strategy， and changed the original greedy strategy in the initialization stage of the algorithm to chaotic distribute the initial pheromone， so as to maintain the diversity of the population and improve the accuracy of the solution. Secondly， the algorithm divided the isolated ants in the ant colony into isolated ant colony and normal ant colony， and the two groups of ants searched around the current optimal path and the outlier path respectively. It adopted the induction mechanism among the populations. Normal ants were responsible for searching the optimal path， and isolated ants released pheromones randomly in chaos to induce the normal ant colony to a new path， thus effectively balancing the contradiction between the convergence rate and the diversity of solutions. The simulation results of different scale TSP show the effectiveness of the proposed algorithm.

Key words：traveling salesman problem; ant colony optimization; dynamic differentiation strategy; chaos random; induction strategy

0 引言

旅行商問题是一种组合优化问题，其目的是给定一组城市的坐标，求出遍历所有坐标并返回起始位置的一条最短路径。旅行商问题是一种NP难问题，在运筹学与计算机科学中具有非常重要的地位。目前有许多算法被提出用于解决TSP问题，如模拟退火（simulated annealing，SA）、遗传算法（genetic algorithm，GA）、蚂蚁算法（ant system，AS）［1］等。其中蚂蚁算法在TSP上有较好的效果。

蚂蚁算法是意大利学者Dorigo提出的一种启发式全局搜索算法，通过模仿自然界中蚂蚁释放信息素寻路的过程实现路径搜索。蚁群算法具有分部性、随机性、动态性等优良性能，并且具有很好的可移植性［2］，能被应用在不同种类的问题上。目前被广泛应用于车间调度［3］、路径规划［4］、路由问题［5］和求解旅行商问题［6］上。传统蚂蚁算法存在一定的局限性。例如蚁群算法在搜索初期缺乏信息素，延迟了算法的收敛速度。在算法的中后期，由于信息素大量积累在部分路径，导致固定路径的选择概率过高，容易使算法陷入局部最优，影响解的质量。于是Dorigo等人[7]在蚂蚁算法的基础上提出了蚁群算法（ant colony system，ACS）提出了全局信息素更新，加快了求解TSP时的速度。Stutzle等人［8］在2000年又提出最大—最小蚁群算法（max-min ant system，MMAS），设置了每条路径上的信息素上下限，提高了解的质量。

针对算法收敛速度慢的问题，许多学者在蚁群算法的基础上作出了改进。文献［9］引入了信息熵理论，通过计算信息熵判断蚁群的离散度，根据系统的离散程度调整算法参数提高解的性能。但是在前期信息熵浓度较低时，不能很好拓展解的多样性容易导致在前期陷入局部最优。文献［10］利用贪心算法求解蚁群算法的初始解，然后计算初始解的次优解，对次优解也给予一定的信息素奖励，加快了解的收敛速度。同时在算法后期引入变异操作，选取当前最优路径附近的路径进行加权。然而，根据贪心算法计算得出的最优解与次优解有可能与真实最优解距离较远，有可能在算法的初期陷入局部最优。在算法容易陷入局部最优解的问题上也有许多改进算法被提出，文献［11］融合狼群算法的分级策略，依据解的大小将蚁群分为不同等级的蚂蚁，并根据不同蚂蚁的地位分配不同的权重，使精英蚂蚁能够分泌更多的信息素，对蚁群起指导作用。文献［12］在结合精英蚁群机制的基础上加入了头狼算法，即对每一个蚂蚁加入搜索半径，精英蚁选择搜索半径内的任意一个节点进行跳变。同时在陷入局部最优后对局部最优节点的信息素进行稀释，达到跳出局部最优的目的。但精英策略在搜索时搜索速度较慢，经常导致算法的运行时间过长。文献［13］在精英策略的基础上增加了自适应分组策略，各个组蚂蚁的数目能够动态调整并在组间增加了学习策略，但自适应分组只是将蚂蚁分为数量不同的组，并没有对每组蚂蚁进行分工。文献［14］将3opt搜索算法与改进蚁群算法相结合，利用3opt算法的近邻搜索能力拓展搜索空间，在保证搜索速度的同时提高了算法的局部搜索能力。文献［15］提出一种刺激响应机制，根据不同任务设置响应阈值，按照不同任务刺激的大小对蚂蚁进行分工，当任务刺激超过某只蚂蚁的响应阈值后将该蚂蚁分配至对应任务，同时引入正负反馈调节机制，根据种群多样性利用正负反馈调节蚂蚁数量，平衡了收敛速度与全局搜索能力，但以上几种算法面对大规模TSP时往往效果不好，收敛速度慢，且容易陷入局部最优解。

针对上述蚁群算法搜索速度慢，在大规模问题上解的精度不高等问题，本文通过加入以下策略提出一种引入动态分化和邻域诱导机制的双蚁群优化算法（ICACO）。在搜索的前期引入混沌随机策略［16］，使地图中的信息素和蚂蚁的位置进行混沌随机更新，取代传统蚁群算法初始化时的贪心策略［10］，在搜索前期使信息素随机地散布在各条路径上以增加解的多样性；其次，提出一种孤立分化机制，首先，根据信息素、路径长度构建归一化模型，按照信息素的分离度使蚁群分为正常种群和分化种群，正常种群沿当前信息素最大的路径探索，孤立种群沿新路径进行搜索，并在新路径上混沌更新信息素值，一旦发现更优路径即释放更多的信息素于更优路径上并将正常种群引导至新的路径。实验结果表明，本文算法相比于原始算法提高了收敛速度和解的质量，在大规模TSP上表现更好。

1 相关工作

1.1 蚁群算法（ACS）

蚁群算法是一种模拟自然界蚁群觅食行为的启发式算法。蚂蚁在觅食过程中会留下信息素，其他蚂蚁在前进时会更大概率选择信息素浓度较高的路径。相同时间内在较短路径上积累的信息素变多，蚁群便找到最短路径，在旅行商问题上有很好的表现。蚁群算法相对于最初的蚂蚁算法（AS）增加了信息素的局部挥发。即每只蚂蚁走过一段路径后，其留下的信息素就会立即挥发一部分，而非全体蚂蚁走过后信息素的全局挥发。其更新规则为

其中：τ（i，j）为节点i到j之间的信息素；ρ是信息素的局部挥发率；Δτ（i，j）为节点i与j之间的信息素增量；释放信息素后，蚂蚁按照式（2）选择下一个节点。

其中：pkij表示蚂蚁k从节点i到j的概率；τij（t）表示节点i到j之间t时刻的信息素总量；η表示节点i到j之间距离的倒数;β为权重因子，代表启发信息对路径选择的影响程度，β越大则启发信息对路径选择的影响程度越大；allowedk表示蚂蚁k还未走过的节点。所有蚂蚁遍历过一次后进行信息素的全局更新，对所有路径上的信息素进行更新，更新方式如式（5）所示。

其中：α为全局信息素挥发系数，代表上一次迭代后信息素的残留比例；Q为信息素更新权重;dbest为全局最短路径；ACS在全局信息素更新时只留下全局最优蚂蚁的信息素。并且随着迭代次数的增加，最优路径上的信息素不断累加，会导致算法陷入局部最优。

1.2 动态分级的改良蚂蚁算法

为了解决传统蚁群算法收敛速度慢的问题，文献［9］提出一种动态分级的蚂蚁算法，按照分级因子将蚂蚁分为四个等级，根据等级的高低为蚂蚁划分不同的信息素更新权重，等级高的蚂蚁可以释放更多的信息素，同时又给予等级低的蚂蚁一定的信息素释放量以增加算法的多样性。定义分级因子为

其中：di为蚂蚁遍历所有节点走过的路径长度;dmin为当前最短路径。各个等级的蚂蚁数量随迭代次数调整，其信息素更新方式与式（5）相同，不同之处在于信息素增量Δτ（i，j），定义为

其中：Q1、Q2、Q3为各个等级能释放的信息素总量，处于第一等级的蚂蚁释放信息素最多，依次递减，处于最后一级的蚂蚁禁止释放信息素；n1、n2、n3为各个等级蚂蚁的数量。通过各个等级蚂蚁数量的不断调整最终达到算法的平衡。

1.3 Logistic混沌随机

混沌随机是一种利用混沌映射产生随机数的策略，具有非周期、不收敛的特性，其中应用较为广泛的为Logistic映射，其表达式为

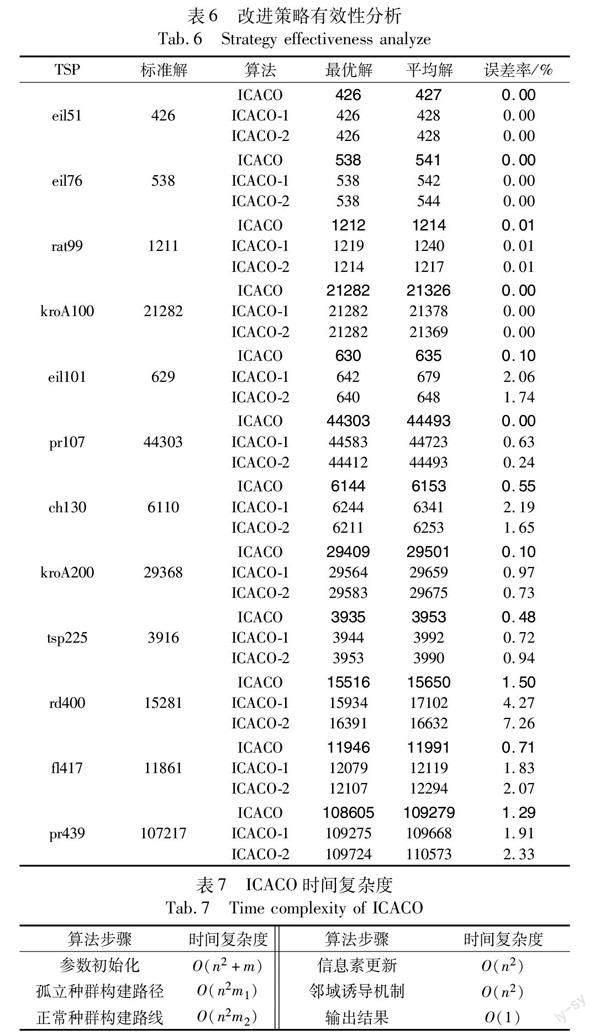
其中：xn+1、xn为混沌序列值;k为混沌因子。混沌序列的作用在于产生一列非线性、不可预测的随机数，这些数字在k取3.569

2 引入动态分化和邻域诱导机制的双蚁群优化算法

2.1 算法的混沌初始化

在蚁群算法的初期，地图上没有信息素，导致算法前期搜索速度慢，同时由于只能利用距离信息初始化算法，导致算法前期易陷入局部最优［8］。并且由于传统产生随机数的策略为伪随机策略，在大规模TSP时不利于种群的搜索多样性。所以在蚁群搜索的前期，在各个城市路径上混沌更新信息素量，使系统前期各个路径上散布随机量的信息素，避免蚁群盲目搜索，增加系统的收敛速度。同时，由于混沌更新的不可预测性与随机性，避免了传统蚁群算法根据贪心算法初始化导致的部分路径完全不会被搜索到，增加了系统解的多样性避免前期陷入局部最优。算法具体更新方式如下：

其中：i为当前迭代次数；当算法第一次迭代时，各个城市间的距离信息作为初始化信息素τ0加上混沌序列产生的随机信息素信息，其中q为混沌调节因子，用于调节系统初始化时的混沌程度，q越大则系统信息素初始化时会更随机。式中c为Logistic混沌参数，c的值越大则混沌程度越大，产生出的随机数更随机，n为总城市数，b为控制因子；当迭代次数小于n/b定义为初始化阶段，在初始化阶段系统信息素更新采用混沌更新方式，保证信息素广泛散播。

2.2 孤立分化策略

2.2.1 孤立策略

传统蚁群搜索的过程存在一定的盲目性，每只蚂蚁都只在信息素浓度最高的路径上搜索，这导致算法只聚焦于搜索最优解而忽视了其他路径，其他路径有可能蕴涵着真正的最优解。在大规模TSP问题中该问题尤其突出。在所有蚂蚁遍历完各城市后，会得到此次遍历路线的总长度，每一只蚂蚁得到的路线和总长度不同。在算法后期，大多数蚂蚁会选择相同的路线，部分蚂蚁会选择新的路线，即使新路线的路径长度大于次优路线长度，这些新路线中可能包含全局最优路径的一部分，本节利用孤立種群策略挑选出走新路线的种群形成孤立种群，然后将信息素与其他个体不同的路线片段提取并加强该路径上的信息素，提高算法的路径选择能力。

孤立种群判定：

在系统经过一定次数迭代后，将对原始种群进行动态分化，迭代次数如式（11）所示。

其中：T1为左阈值，T2为右阈值；Lx是第x只蚂蚁走过的路径长度，Ly是第y只蚂蚁走过的路径长度；m为蚂蚁总数。将所有蚂蚁走过的路径按路径长短从小到大排列，走过路径超过左右阈值的个体被认定为孤立个体。

2.2.2 分化策略

当孤立种群确定后，蚂蚁将分为正常种群和孤立种群，正常种群仍然按照原始路径搜索，孤立种群按照式（16）进行信息素更新，孤立种群在新路径的周围搜索，扩大了解的范围。当发现比当前最优路径更短的路径时，蚁群将释放更多的信息素在更优路径上。孤立种群在最优路径的周围利用Logistic混沌释放随机量的信息素，直到更优路径的产生，并将蚁群引导到新的位置。孤立种群信息素更新方式为

诱导机制：

在对原始蚁群进行分化后，孤立种群将按照式（16）释放信息素。为了更好地扩大搜索空间，本文提出一种诱导机制，当孤立种群找到更优路径后，将原始路径上的信息素清空，加强孤立种群所释放出的信息素浓度并将其扩散，将原始种群引导至孤立种群所发现的新路径周围，施行诱导机制后信息素分布如图4所示。在种群分化后，首先将孤立种群所走过的路线进行one-hot编码［17］，然后与原始路径上的信息素相乘，使信息素矩阵只保留孤立种群所留下的信息素，如图5所示。诱导公式如式（17）所示。

其中：τ为所有路线上的信息素;Li为按照one-hot编码后孤立种群走过的路径矩阵，即将每一步中孤立种群选择的路径置1，未选择的路径置0，使孤立种群释放的信息素扩散至邻域，将蚁群引入新的路径。

2.3 算法流程

a）初始化算法各参数：最大迭代次数imax、各个种群蚂蚁数量m，与α、β、ρ、c等参数，读入城市位置数据。

b）利用混沌序列产生随机数量的信息素分配到各条路径，再利用混沌序列产生每只蚂蚁起始位置。

c）每只蚂蚁按照位置更新公式进行搜索，找到一条完整路径。记录当前迭代最短路径长度。

d）计算路径不变代数是否超过阈值G，若超过则启动孤立分化，选择出孤立种群。

e）分化后的孤立种群按照新的信息素更新方式释放信息素。

f）孤立种群找到更优路径时按照诱导机制将原始种群诱导至新的路径搜索。

g）判断是否达到结束条件，若未达到则返回步骤b）否则结束算法并记录结果。

算法流程如图6所示。

3 实验结果

为了验证和分析本文算法的有效性，选取TSPLIB中几个典型问题进行仿真测试与传统蚁群算法ACS、ACS+3opt进行比较，并与其他同类算法进行比较。在小规模和大规模问题上分别选取不同的算法进行对比，以验证算法在面对大规模问题时的有效性。同时针对算法的收敛速度，将算法与基本蚁群算法（ACS）和ACS+3opt算法在三种不同规模的TSP上进行比较，对比本文算法与其他算法的收敛速度与结果。

3.1 实验环境设置

本文实验环境为：Windows 10操作系统，利用MATLAB 2018a进行仿真。为了验证算法在各个规模TSP问题中的有效性，选择分别与传统蚁群算法ACS与ACS+3opt算法进行不同规模的TSP进行测试。同时选择与目前最新的改进型蚁群算法文献［9，10，18，19］进行对比，分析比较本文算法的改进。实验中算法参数设置如表1所示。

3.2 与传统算法对比结果

首先设置与ACS和ACS+3opt算法进行对比。将各个算法运行10次，比较每种算法在求解TSP时的最优解、平均解、最小误差百分比与收敛时间。其中平均值向下取整，最小误差百分比保留两位小数，设置最大迭代次数为5 000，收敛时间为算法开始到最终收敛所用时间，以秒为单位。结果如表2所示。

通过对比可以看出本文算法在应对小规模问题时有很好的表现，在各个算例中均能找到最优解或与最优解之间最小误差小于1%，并且可以看出实验结果的平均解与最优解之间误差较小，证明了算法的稳定性。在Eil51、Eil76等小规模问题上，ACS、ACS+3opt与ICACO均能找到最优路径，但ICACO平均解的质量优于ACS、ACS+3opt。通过在更大规模旅行商问题上与基本蚁群算法的对比可以看出，随着旅行商问题的规模增大，ACS、ACS+3opt的精度有所下降，而本文算法保持了很好的精度，最优解仍然保持在1%以内的精度，算法的最优解与平均解均优于ACS和ACS+3opt算法。在算法的收敛时间对比上，在小规模TSP问题eil51、eil76、rat99上ACS与ACS+3opt算法的收敛速度快于ICACO，随着TSP的规模不断增大到100以上时，由于动态分化策略能够有效地加快收敛速度ICACO的收敛速度逐渐超过ACO与ACO+3opt，并且随着问题规模的增大，ICACO的收敛速度也越来越高于ACO、ACO+3opt，这是由于随着问题规模的增大ACO与ACO+3opt不可避免地陷入局部最优，导致算法的寻优能力不足，难以找到更优解，而ICACO由于存在邻域诱导机制，可以帮助种群在大规模问题上更好地拓展解空间避免陷入局部最优。

3.3 与最新改进算法对比结果

为了保证实验的客观性，将ICACO与目前最新的改进算法在TSP上进行对比，对比结果如表3所示。表中“-”表示该文未做该实验。由表3可以看出在与当今最新的算法比较时，本文算法仍然有很好的表现。在大中小规模的TSP问题中本文算法最优结果均优于其他算法，在各个问题中均能保证误差在1%左右，随着TSP问题的规模逐渐增大，许多算法已经无法找到结果并且平均解很差。本文算法在处理大规模问题时使用了孤立分化机制，大规模问題中各个算法往往难以避免陷入局部最优，本文算法通过加入诱导机制，在种群陷入局部最优后可以跳出局部最优，增加解的多样性，提高解的质量从而找到更优解。其中部分实验路径结果如图7所示。

3.4 与其他多种群蚁群算法对比

为了体现本文算法的有效性，本文选择了其他多种群蚁群算法进行对比分析。其中文献［13］为自适应分组蚁群算法，根据迭代情况将种群分为不同大小的种群，文献［15］将蚂蚁分为常规蚂蚁和拓展蚂蚁，分别负责搜索效率与搜索广度。

通过表4可以看出，在各个小于100规模的TSP上本文算法性能都优于对比算法，在ch130数据集上最优路径文献［15］算法优于本文算法但本文算法的平均解优于文献［15］算法。从表4可以看出， 由于文献［13］算法只将蚂蚁进行分组而未对其进行不同分工，导致算法解的精度不足，而ICACO将蚂蚁动态分组，调整不同种群蚂蚁的数量的同时设置不同的搜索路线和信息素释放方式，保证两种蚂蚁相互合作，在加快算法收敛速度的同时提高解的质量。文献［15］算法虽然将蚂蚁进行不同分工，但并没有提出跳出局部最优的机制，在算法后期容易陷入局部最优，降低解的精度，而ICACO通过邻域诱导机制，在孤立蚁发现更优路线后将种群诱导至新路线附近，加强对新路线的搜索，在算法后期能够很好地提高解的精度。

表4显示了对比结果，缺失的数据用“-”代替。

3.5 算法性能分析

3.5.1 算法多样性分析

为了证明本文算法增加解的多样性的有效性，通过对比算法在处理TSP问题时每一代路径的长度，对算法的多样性进行分析。实验结果如图8所示。

通过对比算法在运行TSP时每一代路径长度与总路径长度可以看出，算法在陷入局部最优时，利用孤立分化策略增加解的多样性，随着算法后期不可避免地陷入停滞，孤立个体数也在不断增大，算法的解空间也在逐渐增大，最终在算法4 500次迭代后找到了优化解，保证了算法在搜索后期能够跳出局部最优找到更优解。

3.5.2 算法收敛性分析

为了比较算法在收敛速度上的提高，选择在rand400、eil51两个规模的TSP上与ACS、ACS+3opt算法进行实时收敛过程对比，为保证实验准确性选择相同数量的蚂蚁数，在小规模问题的测试中将迭代次数设为5 000次，将大规模问题的最大迭代次数设为2 000次。实验结果如图9所示。

通过对比三种算法在大小两个规模上的运行结果，可以看出本文算法在搜索初期就能很快收敛，最优路径快速迭代，算法不断找到更优解且具有较好的搜索能力。在大规模问题rd400上可以更明显地看出，ACS、ACS+3opt算法在搜索初期就陷入了局部最优，而本文算法在搜索初期采用混沌初始化策略，有效避免了算法在初期陷入早熟。同时在搜索的后期可以看出ACS算法在迭代到一定次数以后便无法找到更优路径，过早陷入局部最优使得在大规模问题时无能为力。而ACS+3opt算法仍不能避免算法在初期就陷入早熟，算法初期的多样性较差，而在算法后期虽然有一定的跳出局部最优解的能力，但由于搜索能力不足同样导致算法陷入局部最优。本文算法在每次迭代初始化时采用混沌随机机制使搜索能力得到加强，同时引入孤立分化机制使迭代后期最优路径长度仍能不断下降，找到更优路径，有较强的跳出局部最优能力使得算法面对大规模问题时有较强的鲁棒性。通过对比三种算法的收敛结果，可以看出本文算法很好地平衡了收敛速度与精度，初期搜索结果快速下降，大大加快了搜索速度，同时后期可以有效地跳出局部最优提高解的精度。

3.5.3 改进策略有效性分析

为分析改进算法中各个策略的有效性，设置算法ICACO-1、ICACO-2与ICACO算法进行对比实验，对每个改进策略进行有效性分析。对比算法使用策略如表5所示。通过在不同数据集上进行对比实验，将结果总结在表6中。其中ICACO-1只使用邻域诱导机制，不对蚂蚁进行分化，所有蚂蚁都设置为正常种群，当有蚂蚁找到更优路径后就会将所有蚂蚁引至新路径。ICACO-2只使用动态分化策略，将蚂蚁分化为正常蚁与孤立蚁，不使用邻域诱导策略进行信息素矩阵更新。

由表6可以看出，在小规模问题eil51、eil76、kroA100上ICACO、ICACO-1、ICACO-2均能找到最优解，而当数据集规模增大，ICACO-2在eil101、pr107、ch130数据集上的表现优于ICACO-1，表明将种群动态分化为正常蚁与孤立蚁能够有效地拓展搜索范围，使算法在搜索阶段具有很好的性能。当数据集规模提升到400以上时算法容易陷入局部最优，而ICACO-1在kroA200、rd400、fl417、pr439数据集上的表现优于ICACO-2，表明邻域诱导机制在大规模问题上能够有效帮助算法避免陷入局部最优。而同时使用动态分化机制和邻域诱导策略的ICACO由于孤立蚁的存在，在解的精度上比单独使用正常蚁进行搜索的ICACO-1提高了50%左右。实验结果ICACO在各个数据集上的表现都比单独使用一种策略的算法优秀，表明動态分化机制和邻域诱导策略能够很好地帮助算法提高搜索能力。

3.5.4 算法复杂度分析

表7中n为节点数;m为蚂蚁总数;m1为孤立蚂蚁数;m2为正常种群个数;i为最大迭代次数。通过表7可知，ICACO的时间复杂度为O（i×n2×m），由此可以看出动态分化机制和邻域诱导机制没有额外增加算法的时间复杂度。

4 结束语

本文分析了现有蚁群算法与几种改进蚁群算法，针对其不足之处提出了一种引入动态分化和邻域诱导机制的双蚁群优化算法。该算法首先将蚂蚁位置和路径上的信息素进行混沌随机，加快了算法的搜索速度；其次通过孤立分化策略将蚂蚁分为原始种群和孤立种群，提高了解的多样性。实验结果表明本文算法在TSP求解上效果良好，尤其针对大规模TSP时也具有很好的表现，但在更大规模的TSP上仍存在收敛速度慢等问题。下一步的研究方向是利用多种群博弈策略解决更大规模TSP。

参考文献：

[1]Dorigo M， Maniezzo V， Colorni A. Ant system： optimization by a co-lony of cooperating agents［J］.IEEE Trans on Systems， Man， and Cybernetics， Part B，1996，26（1）：29-41.

［2]张宏宏，甘旭升，李双峰，等.复杂低空环境下考虑区域风险评估的无人机航路规划［J］.仪器仪表学报，2021，42（1）：257-266.（Zhang Honghong， Gan Xusheng， Li Shuangfeng， et al. UAV route planning considering regional risk assessment under complex low altitude environment［J］.Chinese Journal of Scientific Instrument，2021，42（1）：257-266.）

［3]李燚，唐倩，刘联超，等.基于改进蚁群算法的汽车混流装配调度模型求解［J］.中国机械工程，2021，32（9）：1126-1133.（Li Yan， Tang Qian， Liu Lianchao， et al. An improved ACO algorithm for automobile mixed-flow assembly scheduling problems［J］.China Mechanical Engineering，2021，32（9）：1126-1133.）

［4]包汉，祝海涛，刘迪.基于±3σ正态概率区间分族遗传蚁群算法的移动机器人路径规划研究［J］.控制与决策，2021，36（12）：2861-2870.（Bao Han， Zhu Haitao， Liu Di. Path planning of a mobile robot based on ±3σ normal probability interval population division using the genetic ant-colony algorithm［J］.Control and Decision，2021，36（12）：2861-2870.）

［5]孙明杰，周林，于云龙，等.无人机自组网中基于蚁群优化的多态感知路由算法［J］.系统工程与电子技术，2021，43（9）：2562-2572.（Sun Mingjie， Zhou Lin， Yu Yunlong， et al. Ant colony optimization based polymorphism-aware routing algorithm for Ad hoc UAV network［J］.System Engineering and Electronics，2021，43（9）：2562-2572.）

［6]Pan Han， You Xiaoming， Liu Sheng， et al. Pearson correlation coefficient-based pheromone refactoring mechanism for multi-colony ant colony optimization［J］.Applied Intelligence，2020，51（2）：1-23.

［7]Dorigo M， Gambardella L M. Ant colony system： a cooperative lear-ning approach to the traveling salesman problem［J］.IEEE Trans on Evolutionary Computation，1997，1（1）：53-66.

［8]Stutzle T， Hoos H H. Max-min ant system［J］.Future Generation Computer Systems，2000，16（8）：889-914.

［9]陈佳，游晓明，刘升，等.结合信息熵的多种群博弈蚁群算法［J］.计算机工程与应用，2019，55（16）：170-178.（Chen Jia， You Xiao-ming， Liu Sheng， et al. Entropy-game based multi-population ant colony optimization［J］.Computer Engineering and Applications，2019，55（16）：170-178.）

［10]陈颖杰，高茂庭.基于信息素初始分配和动态更新的蚁群算法［J］.计算机工程与应用，2022，58（2）：95-101.（Chen Yingjie， Gao Maoting. Pheromone initialization and dynamic update based ant colony algorithm［J］.Computer Engineering and Applications，2022，58（2）：95-101.）

［11]陳佳，游晓明，刘升，等.动态分级的改良蚂蚁算法及其应用研究［J］.计算机应用研究，2019，36（2）：380-384.（Chen Jia， You Xiao-ming， Liu Sheng， et al. Research on dynamic hierarchical ant optimization algorithm and its application［J］.Application Research of Computers，2019，36（2）：380-384.）

［12]张毅，权浩，文家富.基于独狼蚁群混合算法的移动机器人路径规划［J］.华中科技大学学报：自然科学版，2020，48（1）：127-132.（Zhang Yi， Quan Hao， Wen Jiafu. Mobile robot path planning based on the wolf ant colony hybrid algorithm［J］.Huazhong University of Science & Technology：Natural Science Edition，2020，48（1）：127-132.）

［13]卜冠南，刘建华，姜磊，等.一种自适应分组的蚁群算法［J］.计算机工程与应用，2021，57（6）：67-73.（Bu Guannan， Liu Jianhua， Jiang Lei， et al. An ant colony algorithm with adaptive grouping［J］.Computer Engineering and Applications，2021，57（6）：67-73.）

［14]Gülcü瘙塁， Mahi M， BaykanK， et al. A parallel cooperative hybrid method based on ant colony optimization and 3-opt algorithm for solving traveling salesman problem［J］.Soft Computing，2018，22（5）：1669-1685.

［15]冯振辉，肖人彬.基于混合反馈机制的扩展蚁群算法［J］.控制与决策，2022，37（12）：3160-3170.（Feng Zhenhui， Xiao Renbin. Extended ant colony algorithm based on mixed feedback mechanism［J］.Control and Decision，2022，37（12）：3160-3170.）

［16]马小陆，袁书生，王兵，等.均匀分布Logistic混沌序列的RRT路径规划算法研究［J］.机械科学与技术，2022，41（4）：610-618.（Ma Xiaolu， Yuan Shusheng， Wang Bing， et al. Research on RRT path planning algorithm for uniformly distributed Logistic chaotic sequence［J］.Mechanical Science and Technology for Aerospace Engineering，2022，41（4）：610-618.）

［17]梁杰，陈嘉豪，张雪芹，等.基于独热编码和卷积神经网络的异常检测［J］.清华大学学报：自然科学版，2019，59（7）：523-529.（Liang Jie， Chen Jiahao， Zhang Xueqin， et al. One-hot encoding and convolutional neural network based anomaly detection［J］.Journal of Tsinghua University：Science and Technology Edition，2019，59（7）：523-529.）

［18]Tuani A F， Keedwell E， Collett M. Heterogenous adaptive ant colony optimization with 3-opt local search for the travelling salesman pro-blem［J］.Applied Soft Computing，2020，97（PB）：106720.

［19]Huang Yao， Shen Xiaoning， You Xuan. A discrete shuffled frog-leaping algorithm based on heuristic information for traveling salesman problem［J］.Applied Soft Computing，2021.102：107085.

收稿日期：2023-02-28；修回日期：2023-04-17

基金项目：国家自然科学基金资助项目（61673258，61075115）；上海市自然科学基金资助项目（19ZR1421600）

作者简介：禹博文（1997-），男，河南郑州人，硕士研究生，主要研究方向为智能算法、机器学习、人工智能；游晓明（1963-），女（通信作者），江苏兴化人，教授，硕导，博士，主要研究方向为群智能系统、分布式并行处理、进化算法（yxm6301@163.com）；刘升（1966-），男，湖北大冶人，教授，硕导，博士，主要研究方向为量子启发式进化算法、分布式并行处理、进化算法.