用于连续时间中策略梯度算法的动作稳定更新算法

宋江帆　李金龙

摘 要：在强化学习中，策略梯度法经常需要通过采样将连续时间问题建模为离散时间问题。为了建模更加精确，需要提高采样频率，然而过高的采样频率可能会使动作改变频率过高，从而降低训练效率。针对这个问题，提出了动作稳定更新算法。该方法使用策略函数输出的改变量计算动作重复的概率，并根据该概率随机地重复或改变动作。在理论上分析了算法性能。之后在九个不同的环境中评估算法的性能，并且将它和已有方法进行了比较。该方法在其中六个环境下超过了现有方法。实验结果表明，动作稳定更新算法可以有效提高策略梯度法在连续时间问题中的训练效率。

关键词：强化学习； 连续时间； 策略梯度； 动作重复

中图分类号：TP389.1 文献标志码：A 文章编号：1001-3695（2023）10-007-2928-05

doi：10.19734/j.issn.1001-3695.2023.02.0092

Action stable updating algorithm for policy gradient methods in continuous time

Song Jiangfan， Li Jinlong

（School of Computer Science & Technology， University of Science & Technology of China， Hefei 230000， China）

Abstract：In reinforcement learning， the policy gradient algorithm often needs to model the continuous-time process as a discrete-time process through sampling. To model the problem more accurately， it improves the sampling frequency. However， the excessive sampling frequency may reduce the training efficiency. To solve this problem， this paper proposed action stable updating algorithm. This method calculated the probability of action repetition using the change of the output of the policy function， and randomly repeated or changed the action based on this probability. This paper theoretically analyzed the perfor-mance of this method. This paper evaluated the performance of this method in nine different environments and compared it with the existing methods. This method surpassed existing methods in six of these environments. The experimental results show that this method can improve the training efficiency of the policy gradient algorithm in continuous-time problems.

Key words：reinforcement learning; continuous time; policy gradient; action repetition

0 引言

强化学习是人工智能領域中的一个重要研究方向，它可以应用于各种不同的应用，有潜力解决很多现实世界的问题，例如智能机器人、金融或自动驾驶。经典的强化学习算法将环境建模为离散时间马尔可夫决策过程。然而在很多现实问题中，时间是连续的，处理连续时间的强化学习算法还不够成熟。

在强化学习中，已经提出了一些专门针对连续时间马尔可夫决策过程的算法［1～3］。这些算法都是针对特定问题设计的，它们增加了各种不同的关于转移函数和奖励函数的先验假设。例如在自适应控制领域，提出了大量基于连续时间的算法［4～8］。自适应控制可以看成是强化学习的一个特例。在自适应控制中，经常假设状态关于时间是可微的，并且状态关于时间的微分方程符合一些特定的形式，比如假设微分方程是线性的。有了这些假设，模型的训练会简单很多。在自适应控制中，通常从一个确定性的初始策略开始，通过迭代优化算法来获得最优策略，而不需要随机探索。

目前，连续时间马尔可夫决策过程的通用算法仍然大量使用的是基于离散时间的强化学习算法。这类算法需要以一定的时间间隔τ来对时间进行采样，并将问题建模为离散时间过程。时间间隔τ决定了智能体决策的频率，并且会影响强化学习的效果［9，10］。具体来说，一些实际应用需要智能体的反映尽可能快，例如自动驾驶，而时间间隔会影响智能体的反映时间。为了减少反映时间，时间间隔需要尽可能小。然而对于基于离散时间的算法，过小的时间间隔会导致新的问题。在基于Q值的强化学习算法中，当时间间隔趋于零时，同一状态的不同动作对应的Q（s，a）会趋向于同一个值V（s），从而导致算法无法正确学习策略。为了解决这个问题，有人提出了advantage updating ［11］，它通过使用公式［Q（s，a）－V（s）］/τ替代Q（s，a）来解决这个问题。之后，有人将advantage updating结合到了深度神经网络中［12］。

对于基于策略梯度的算法，减小时间间隔τ会增加动作改变的频率，这会导致增加优势函数的相对误差［12，13］和降低智能体的探索效率两个新问题。为了解决这两个问题，最朴素的方法是选择一个合适的时间间隔［10］。除此之外，如果动作空间连续，那么可以使用自相关噪声代替策略函数中的白噪声控制动作改变的幅度，来达到类似于减小动作改变频率的效果［14～16］。对于一般性的动作空间，可以使用动作重复来解决动作改变频率过高的问题，也就是让智能体自己决定动作持续的时间或重复的次数［13，17］。其中最简单的方法是让智能体自己输出动作重复的次数，即FiGAR（fine grained action repetition）［17］。然而，这种方法会导致智能体在状态有突发变化时无法立刻响应［13］。为了解决这个问题，有人提出了SAR（safe action repetition）［13］。SAR使用一个额外的策略函数π（d|s）输出状态改变量的一个阈值d，动作会一直重复到状态的变化超过d。然而在很多环境中，状态的改变量无法定义（例如状态是一幅图片），使得SAR无法应用。

在这些动作重复方法中，需要计算重复次数或者状态改变量的阈值，然而，这些变量的最优值很难计算。因为这些变量不仅影响训练效率，同时也影响奖励。如果只使用奖励来训练神经网络去估计重复次数［17］或状态改变量的阈值［13］，那么就会忽略掉对训练效率的影响。神经网络可能会为了更高的奖励输出较小的值，从而降低模型的训练效率。与SAR不同，本文提出了一个根据动作分布改变量随机决定动作是否重复的新方法。

为了改进现有动作重复方法的问题，提出了动作稳定更新算法。对于大多数强化学习任务，状态空间的大小远大于动作空间，因此在不同状态下的最优动作可能是相同的。所以当状态发生改变时动作不一定需要改变。与SAR不同，该算法通过使用策略函数的改变量判断动作是否有必要重复。由于不需要计算状态的改变量，所以可以应用在状态距离无法定义的环境，从而解决了SAR的主要问题。为了降低模型的训练难度，该方法不训练额外的神经网络来确定动作的持续时间，而是根据策略函数输出动作分布的改变量决定动作是否重复的概率，并根据该概率随机地重复或改变动作。策略函数的输出变化越大，改变动作的概率也越大。

本文的贡献包括如下方面：

a）提出了动作稳定更新算法来解决基于策略梯度的强化学习算法在连续时间问题中动作变化频率过高的问题，该方法可以应用于一般化的强化学习问题。在动作稳定更新算法中，动作重复的概率取决于策略函数在每一步输出的动作分布相对于上一步的改变量。

b）在理论上证明了该方法有两个优良性质：（a）智能体可以立刻响应状态的变化;（b）在正常情况下，无论时间间隔如何变化，动作改变的频率都是有界的。目前为止，动作稳定更新算法是唯一同时满足这两个性质的算法。

将动作稳定更新算法应用到了PPO2［18］和MAPPO［19］，并在多种不同的环境中进行了测试。测试环境来自于OpenAI Gym［20］、Atari［21］和StarCraft multi-agent challenge（SMAC）［22］。实验结果显示，该方法可以在大多强化学习任务中有效提升基于策略梯度的强化学习算法的性能，并且在大部分环境下超过了之前的SAR和FiGAR。

对于不使用动作重复的策略梯度法，满足瞬时性而不满足稳定性。对于FiGAR［17］或SAR［12］，满足稳定性而不满足瞬时性。就目前而言，动作稳定更新算法是唯一同时满足这两个性质的算法。

4 实验

为了探究动作稳定更新算法是否可以更好地解决连续时间马尔可夫决策过程，将该方法应用到了PPO2［18］和MAPPO［19］，并在如下环境中进行了测试：OpenAI Gym［20］、Atari［21］和StarCraft multi-agent challenge（SMAC）［22］。

4.1 实验环境

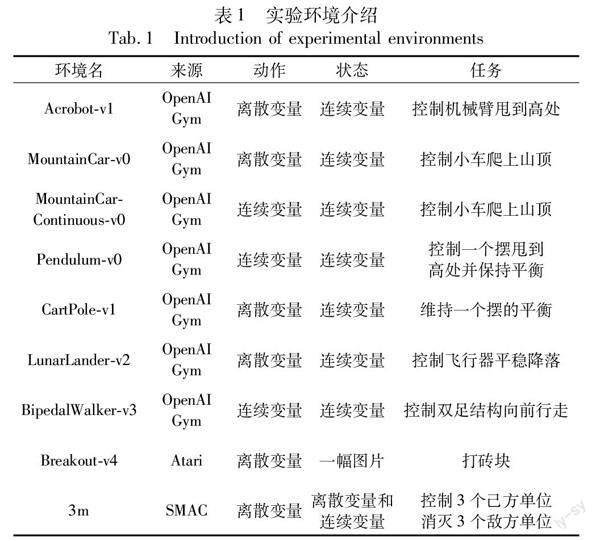
在九个不同环境中评估了动作稳定更新算法。所有环境参数设置为默认值。不同环境的动作空间、状态空间和任务各不相同，如表1所示。

4.2 對比方法和实验设置

实验对比了FiGAR［17］、SAR［13］和没有动作重复的策略梯度法。SAR的状态距离函数和原文保持一致，即‖1－2‖1/dim（S），其中‖·‖1是L1范数，是根据平均值和方差归一化之后的状态。自适应随机动作重复的超参数ε为0.2/τ，SAR的超参数dmax为0.5，FiGAR的超参数dmax为10τ，其中τ为环境默认的时间间隔。

实验参数如下：实验中16个环境并行运行；每更新一次每个环境执行128步；奖励调整为原始奖励的百分之一；学习速率为0.004；每次更新迭代10次；神经网络除Breakout外使用多层全连接网络，深度为2，隐藏层大小为64。

4.3 简单环境下的实验结果

为了对比不同算法性能差异，在来自OpenAI Gym［20］的七个简单环境下进行了测试，如图1～7所示。其中横轴代表训练所经过的环境步数，纵轴代表总奖励的平均值，每条曲线为五次运行取的平均值。“+our”代表动作稳定更新算法。

这七个环境可以分为三类：第一类环境需要动作改变的频率较低，包括MountainCar和MountainCarContinuous；第二类环境需要动作的改变频率较高，这样才能获得较高的奖励，包括BipedalWalker和CartPole；剩下的为第三类环境，它们对动作频率没有明显的要求，包括Acrobot、Pendulum和LunarLander。之后将分别讨论不同算法在这三类环境下的表现。

如图1、2所示，对于第一类环境，动作稳定更新算法和FiGAR表现较好，这可能是因为它们能够保持动作的稳定。相比于FiGAR，动作稳定更新算法的效果更好一些，这可能是因为动作稳定更新算法在保持动作稳定的同时还保证动作的瞬时性，即动作可以立刻对状态的变化作出反应。

具体来说，在环境MountainCarCountinous-v0中，每执行一个动作都会得到一个负的奖励除非什么都不做，这使得它很容易陷入局部最优，此时需要保证动作的稳定来增加探索效率。如图1所示，PPO2获得的奖励总是最低，似乎是陷入了局部最优。而PPO2+FiGAR和PPO2+our总能得到最高的奖励。PPO2+SAR比PPO2好一些，可能是有一定概率陷入局部最优。

在环境MountainCar-v0中，如果动作改变频繁的话探索效率会很低。如图2所示，这个问题可以通过动作稳定更新算法或FiGAR解决。虽然SAR也是一个动作重复方法，但是它无法解决这个问题，这主要是由于状态的距离难以定义。SAR在计算距离时使用state的方差进行归一化，但是在训练中状态的方差是不断变化的，这导致了状态的改变量无法正确计算。

对于第二类环境，即需要动作的改变频率较高的环境，由于不存在动作改变频率过高的问题，所以直接使用原始PPO2算法即可。但是因为可能无法事先知道环境是否属于第二类，所以依然希望各种算法在这类环境能够表现良好。

如图3、4所示，对于第二类环境，原始PPO2的表现最为出色，这与理论上的分析结果一致。SAR的结果比FiGAR和动作稳定更新算法的结果更好，这可能是因为FiGAR和动作稳定更新算法倾向于让动作保持稳定，使得动作的改变频率过低。相比之下，SAR的动作改变频率更高一些，所以没有落后原始PPO2太多。

在第三类环境中，没有对动作改变频率的特殊要求。图5～7展示了不同算法在第三类环境中的表现。其中动作稳定更新算法略好于原始PPO2，为表现最好的算法。这主要是因为动作稳定更新算法具有瞬时性，这使得该算法在保持动作稳定的同时可以立刻对状态的变化进行响应，所以表现通常不会比PPO2更差;又由于该算法保持了动作的稳定，所以一定程度上提高了训练效率。而SAR的表现最差，这可能是因为状态间的距离难以准确计算。

4.4 复杂环境下的实验结果

设计动作稳定更新算法的一个原因是SAR不能用在状态距离难以定义的复杂环境中。为了探究动作稳定更新算法是否可以应用于一般环境，在Breadout-v4和SMAC中的3m中评估了动作稳定更新算法。其中Breakout-v4的状态是一个图片；SMAC是一个多智能体环境，时间间隔设置为一帧。FiGAR在多智能体环境中会同时输出多个不同的时间间隔，这使得不同智能体的同步存在一些困难，所以SMAC中没有测试FiGAR。实验结果如图8、9所示。其中横轴代表环境步数，纵轴代表总奖励的平均值，每条曲线为五次运行取的平均值。“+our”代表动作稳定更新算法。

对于Breakout-v4，图8展示了PPO2、PPO2+our和PPO2+FiGAR的对比结果。PPO2+our的表现超过了PPO2+FiGAR并和PPO2类似。对于SMAC的3m，图9展示了MAPPO和MAPPO2+our的结果，其中MAPPO为多智能体环境下的基于策略梯度的强化学习算法。动作稳定更新算法明显提升了MAPPO的表现，尤其是在频率高的情况下。

这些结果显示动作稳定更新算法可以应用于一些复杂的环境。由于该方法是根据策略函数来判断動作是重复还是更新，所以只要策略函数可以运行该算法就可以使用，这使得该方法应用范围更广。

4.5 实验总结

根据以上实验，可以结合理论分析得出不同算法的优缺点，如表2所示。

5 结束语

为了提升基于策略梯度的强化学习算法解决连续时间马尔可夫决策过程的能力，提出了动作稳定更新算法。该方法让策略梯度法可以在不影响训练效率的前提下减小响应时间，从而提升整体性能，并且该方法可以应用于一般的连续时间马尔可夫决策过程问题，证明了该方法的瞬时性和稳定性。在实验中，将动作稳定更新算法应用到了来自于OpenAI Gym、Atari和SMAC的九个不同的环境中，实验结果显示该方法在大部分环境下表现得更好。

理论上，如果策略函数是最优的，动作稳定更新算法可以选择合适的重复次数。然而，如果策略函数没有经过充分的训练，动作重复的次数可能过多。这可能是动作稳定更新算法在实验中的两个环境上表现差的原因。在策略经过充分训练之前选择合适的重复次数仍然是一个问题。

参考文献：

[1]Munos R. Policy gradient in continuous time［J］.The Journal of Machine Learning Research，2006，7：771-791.

［2]Wang Haoran， Zariphopoulou T， Zhou Xunyu. Reinforcement lear-ning in continuous time and space：a stochastic control approach［J］.Journal of Machine Learning Research，2020，21（1）：8145-8178.

［3]唐波，李衍杰，殷保群.连续时间部分可观Markov决策过程的策略梯度估计［J］.控制理论与应用，2009，26（7）：805-808.（Tang Bo， Li Yanjie， Yin Baoqun. The policy gradient estimation for continuous-time partially observable Markovian decision processes［J］.Control Theory & Applications，2009，26（7）：805-808.）

［4]Du Jianzhun， Futoma J， Doshi-Velez F. Model-based reinforcement learning for semi-Markov decision processes with neural ODEs［J］.Advances in Neural Information Processing Systems，2020，33：19805-19816.

［5]He Shuping， Fang Haiyang， Zhang Maoguang， et al. Adaptive optimal control for a class of nonlinear systems：the online policy iteration approach［J］.IEEE Trans on Neural Networks and Learning Systems，2019，31（2）：549-558.

［6]Modares H， Lewis F L， Jiang Zhongping. Tracking control of completely unknown continuous-time systems via off-policy reinforcement learning［J］.IEEE Trans on Neural Networks and Learning Systems，2015，26（10）：2550-2562.

［7]Vamvoudakis K G， Lewis F L. Online actor-critic algorithm to solve the continuous-time infinite horizon optimal control problem［J］.Automatica，2010，46（5）：878-888.

［8]Vrabie D， Pastravanu O， Abu-Khalaf M， et al. Adaptive optimal control for continuous-time linear systems based on policy iteration［J］.Automatica，2009，45（2）：477-484.

［9]Braylan A， Hollenbeck M， Meyerson E， et al. Frame skip is a power-ful parameter for learning to play Atari［C］//Proc of the 29th AAAI Conference on Artificial Intelligence.Palo Alto，CA：AAAI Press，2015：10-11.

［10]Zhang Zichen， Kirschner J， Zhang Junxi， et al. Managing temporal resolution in continuous value estimation：a fundamental trade-off［EB/OL］.（2022-12-17）.https：//arxiv.org/abs/2212.08949.

［11]Baird L C. Reinforcement learning in continuous time： advantage updating［C］//Proc of IEEE International Conference on Neural Networks.Piscataway，NJ：IEEE Press，1994：2448-2453.

［12]Tallec C， Blier L， Ollivier Y. Making deep Q-learning methods robust to time discretization［C］//Proc of the 36th International Confe-rence on Machine Learning.［S.l.］：PMLR，2019：6096-6104.

［13]Park S， Kim J， Kim G. Time discretization-invariant safe action repetition for policy gradient methods［J］.Advances in Neural Information Processing Systems，2021，34：267-279.

［14]Korenkevych D， Mahmood A R， Vasan G， et al. Autoregressive policies for continuous control deep reinforcement learning［EB/OL］.（2019-03-27）.https：//arxiv.org/abs/1903.11524.

［15]Lillicrap T P， Hunt J J， Pritzel A， et al. Continuous control with deep reinforcement learning［EB/OL］.（2019-07-05）.https：//arxiv.org/abs/1509.02971.

［16]Wawrzynski P. Control policy with autocorrelated noise in reinforcement learning for robotics［J］.International Journal of Machine Learning and Computing，2015，5（2）：91-95.

［17]Sharma S， Srinivas A， Ravindran B. Learning to repeat： fine grained action repetition for deep reinforcement learning［EB/OL］.（2020-09-21）.https：//arxiv.org/abs/1702.06054.

［18]Schulman J， Wolski F， Dhariwal P， et al. Proximal policy optimization algorithms［EB/OL］.（2017-08-28）.https：//arxiv.org/abs/1707.06347.

［19]Yu Chao， Velu A， Vinitsky E， et al. The surprising effectiveness of PPO in cooperative，multi-agent games［EB/OL］.（2022-11-04）.https：//arxiv.org/abs/2103.01955.

［20]Brockman G， Cheung V， Pettersson L， et al. OpenAI Gym［EB/OL］.（2016-06-05）.https：//arxiv.org/abs/1606.01540.

［21]Bellemare M G， Naddaf Y， Veness J， et al. The arcade learning environment：an evaluation platform for general agents［J］.Journal of Artificial Intelligence Research，2013，47：253-279.

［22]Samvelyan M， Rashid T， De Witt C S， et al. The StarCraft multi-agent challenge［EB/OL］.（2019-12-09）.https：//arxiv.org/abs/1902.04043.

收稿日期：2023-02-27；修回日期：2023-04-06

作者簡介：宋江帆（1999-），男，河南新密人，硕士研究生，主要研究方向为强化学习；李金龙（1975-），男（通信作者），安徽合肥人，副教授，硕导，博士，主要研究方向为机器学习、大数据分析、强化学习（jlli@ustc.edu.cn）.