基于单天线相位的UHF RFID室内定位算法研究

陈港能,朱洪辉

(1. 漳州理工职业学院印刷传媒与艺术学院,福建漳州,363000;2. 漳州理工职业学院机电与信息学院,福建漳州,363000)

射频识别技术(RFID)属于无线非接触式系统,对目标的识别是通过射频信号自动完成的,以此来获取相应的目标信息[1]。通过研究可知RFID 系统是由标签、阅读器、天线3 个部分组成。该系统的优势是非接触、非视距。UWB、超声波、WiFi 等[2]现已成为室内定位时常用的技术,相比于这些技术,UHFRFID 定位系统的成本较低[3]。经过与有源RFID 系统进行比较可以看出无源RFID 系统的优势更加显著,由于标签较轻使得携带更加方便,不需要对标签电源进行内置处理。在对定位进行衡量时涉及多个指标,定位误差是不可避免的[4]。对有源RFID 定位系统进行研究后发现其亟待解决的是定位误差较高的问题。如果将传统定位技术应用于室内定位之中,则要面对硬件成本高和覆盖范围小等困扰[5]。受移动通信技术和物联网速度不断加快的影响,在室内定位领域技术中,基于RFID 的室内无线定位技术因其非视距、灵敏度高、环境适应力较强等特点成为优选[6]。因室内环境有多径效应、噪声干扰的影响存在,现有RFID 室内定位方案存在定位精度较低、过于依赖网络等缺陷。因此,本文基于单天线相位的UHF RFID,对室内定位算法进行了研究。

1 载波相位与副载波相位

展开相位信息的提取可通过多载波信号方式进行,可对绝对信号传播距离进行计算,展开相位信息受多途径传播环境影响,与绝对距离间存在较大误差[7]。在单频副载波调幅方式下,假设发射出频率的3 个高频载波信号分别为fc-fs、fc、fc+fs,其中fc-fs为初始载波信号频率,fs为副载波信号频率; 在多途径传播环境中,如果视距与非视距传播路径中信号传播距离已经确定,分别记为dlos和di,则多径传播信道增益为:其中,Γi表示网络输入端的反射系数。

3 个高频载波信号相位值φc-s、φc、φc+s可分别表示为:

其中,kc-s、kc、kc+s分别表示3 个载波对应的k值,βc-s、βc、βc+s分别表示在视距传播路径中3 个高频信号累积的相位信息。通过提取3 个高频载波信号的相位信息,可以计算副载波信号和载波信号之间的多路径频率和相位偏移率。

1.1 副载波相位偏移量计算

副载波相位的计算公式为φs=(φc+s-φc-s)/2,相应传播距离为ds=(φs/(2πfs))·c,标签位置距离为Ds=ds/2=m·(λc/2)+l1,其中初始载波信号fc的波长为λc;m为正整数,半波长范围内的l1∈[0,λc/2]。

1.2 载波相位偏移量计算

基于载波信号fc的相位值φc,信号传播距离的计算公式为

鉴于在实际提出的载波信号相位信息中出现周期模糊的问题,实际信号传播距离计算公式为其中,[·]为下取整运算。

基于φc估计出的标签位置距离为

1.3 计算阅读器和标签真实间距

设d为阅读器与标签之间的真实间距,引入d和载波fc的波长λc的关系式:

式(1)中,n为正整数,半波长范围内的l2∈[0,λc/2]。

1.4 标签位置距离与真实距离之间的关系

做出如下假设:n≤m,以副载波信号、载波信号相位信息为基础可得到标签位置距离与真实距离间的关系,具体见图1。

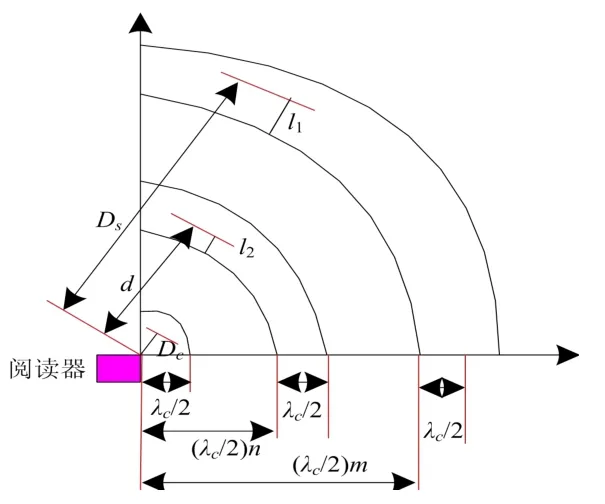
图1 信号距离关系图

副载波相位信息因受多途径传播信道影响有误差存在,直接测距则误差较大[8]。由于在m值和n值间存在较大测距误差,在l1值和l2值间存在较小误差。不使用参考标签时,提高基于相位信息测距精度的关键在于减少m值和n值间差异。在多途径传播环境中的相邻位置处,分析m值、n值差异,载波信号相位信息测距值Dc∈[0,λc/2]。在多途径传播环境中对Dc值与l2值的差异进行研究,需要比较的是l1值和Dc值在0～λc/2 范围内准确性的情况。

假设载波频率fc为921 MHz,副载波频率fs为2.5 MHz; 在y轴方向上,以1.5～6.5 m 作为阅读器和标签距离d的变化范围,以1 m 作为步长; 在距y轴同一距离d之上放置2 个标签,其位置在x轴方向上,标签1 与标签2 的坐标分别为(2.2,d)、(2.365,d)。由此可以做出判断,标签1 与标签2 在x轴上的距离确定为0.165 m,该数值与λc/2相接近,即为1/2 载波波长; 假设墙面与阅读器距离为4.5 m,有2 条传播路径在阅读器和每个标签通信之中存在,一条是墙面反射的非视距传播路径,另一条是墙面反射视距传播路径,其中地面介质相对介电常数r为5,电导率σ为0.002。表1 为m值和n值的差异。

由表1 可知,n值和m值间无绝对大小关系,这表明对于测距误差而言,多途径传播产生的影响不易估计。将标签1、标签2 的m值求平均,可在一定程度上将n值、m值间的部分差异减少。在定位场景中,阅读器和标签2 间的距离大于其和标签1 的距离,以标签1 作为标签2 的m值补偿,以此来保证标签1 与标签2 阅读器位置方向关系。表2 为半波长范围内l1值、l2值和Dc值的差异。

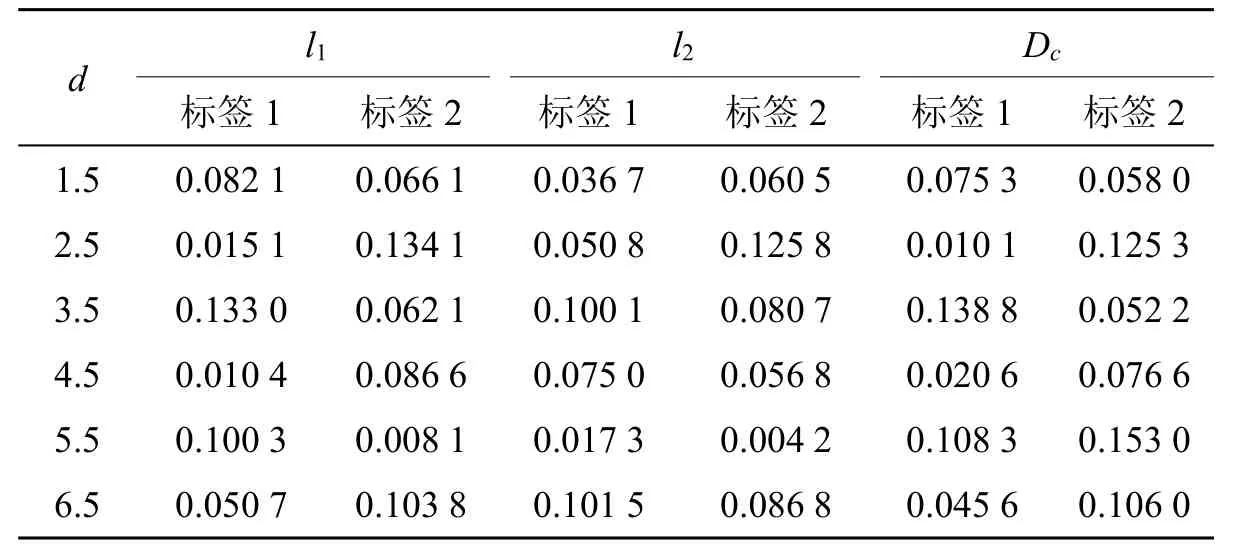
表2 半波长范围内l1 值、l2 值和Dc 值的差异 /m

由表2 可知,标签1、标签2 的Dc值与l2值大小关系一致,标签1、标签2 的l1值与l2值间具有明显差异,总体而言,Dc值比l1值要优。在d=5.5 m 时,标签1、标签2的Dc值与l2值有差异存在,34×(λc/2)+0.008 1=33×(λc/2)+0.153 0 为标签2 与阅读器间真实距离,标签1、阅读器间真实距离为33×(λc/2)+0.100 3。若采用联合标签1、标签2 的m值求平均方式,结合标签1、标签2 的Dc值,则阅读器、标签2 估计距离为33.5×(λc/2)+0.153 0; 阅读器、标签1 间估计距离为33.5×(λc/2)+0.108 3; 标签1、标签2 估计距离比实际距离0.5×(λc/2)要大,标签2、阅读器间距离大于标签1 距离真实情况得到保证。结合表1、表2 实验结果,提出基于双标签两步测距定位方法。

2 基于双标签的测距定位方法

通常情况下,运用在仓储空间条件下的待定位目标的体积都比较大,诸如大尺寸的纸箱和大容量编织袋,而无源标签体积则很小,使用无源标签体积为5.50 cm×5.50 cm×0.03 cm; 在大体积待定位目标上,附着无源标签两个定位[9]。如果2个标签处于较近的位置,则多途径传播的环境把求平均运算与载波相位信息两种方法结合起来使用,可以使副载波相位偏移量的测距误差随之减少[10]。

2.1 基于双标签的测距方法

以往研究中侧重于信号展开相位信息,较为忽视存在周期模糊的卷叠相位信息,本文使用将信号的卷叠相位信息、展开相位信息相结合的测距算法。假设在同一平面上,待定位目标附着标签1、标签2,图2为双标签法二维平面图。1–d 为标签1 阅读器的视距距离,2–d 为标签2 的相应距离。在多途径传播信道,因有相位偏移引入,视距距离1–d、2–d 是由标签1 与标签2 所做出的估计,与实际距离存在偏差。

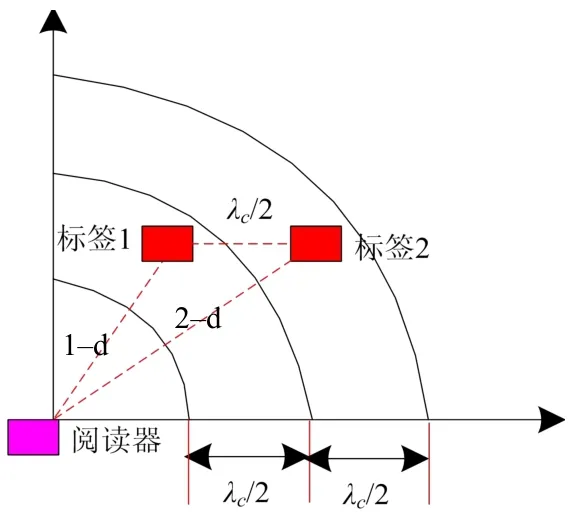
图2 双标签法

结合表1,视距传播路径不同,标签的距离比较接近,但是相位偏移的问题会受到多途径传播的影响而产生,且问题较为显著。所以在本次研究中提出采用双标签两步测距的方法,根据副载波信号相位信息得到距离计算正整数mi,其计算公式为其中,[·]为下取整,i∈{1,2}为双标签编号。

对双标签各自对应的正整数m1、m2进行计算。相比于式(1)中准确的正整数值n,m1和m2均有偏差存在,求m1和m2的平均值m,减少差异,即

利用载波相位计算距离Dc,i,设ai为标签i阅读器的距离估计值,则可由下式求得估计距离m:

这里采取的是同时附着双标签部署的方法,提取副载波信号相位信息是在待定位目标上完成的,对2 个标签与阅读器间的距离进行估计。

2.2 基于双标签的定位方法

在传统几何定位方法中,使用多个阅读器方式,在待定位区间的不同方位处分布阅读器,通过圆相交方式对待定位标签坐标位置做出准确的估计[11]。双标签处于三维空间内可以进行拓展后成为三标签。假设(x,y)为待定位目标坐标,标签1 坐标为(x1,y1),标签2 坐标为(x2,y2),Δd为标签1 和标签2 间的间隔,在Δd=λc/2 的条件下,为了确定标签1、标签2 阅读器天线与(0,0)的距离(分别记为a1、a2),可以把两步测距的方法应用于其中,即

标签1、标签2 的坐标关系满足:

计算出标签1 的坐标解为

再利用公式x=(x1+x2)/2,y=(y1+y2)/2,解得标签2 的坐标解x2,y2。其中,(x,y)为待定位目标的坐标。坐标x1＜0 的情况很可能在式(5)中产生,之所以出现这种问题是由于所采取的是两步测距法,以式(2)为依据确定标签1 和标签2 正整数是一致的。比较标签2 与标签1 后,前者正整数m2比后者正整数m1多1,在式(2)后,标签2、标签1 具有相同的正整数,这样会减小标签2 与阅读器距离。标签2 与阅读器的距离在数值上差半波长λc/2,因标签1、标签2 间坐标满足式(4),会使定位结果有较大误差出现,而这些误差对于某些应用场景则会产生一定的影响。比如在登记仓储入口处的物品时,如果物品已被阅读器左半面空间进行了登记,那么右半面属于需登记物品,而右半面空间内包括了标签1 和标签2,但是受到距离误差的影响而做出错误的判断,将其划归为左半面,即已登记货物,这会引发货物登记混乱,需修正。在进行标签位置误判修正时,标签1、标签2 间距离为半波长λc/2,可确保标签2 与阅读器距离一直超过标签1 与阅读器的距离,能够精确把标签2 与阅读器距离中的半波长数倍展示出来,即与标签1 相应距离中的半波长整数倍进行比较要超出1。所以标签2 在x1＜0 的条件下距离a2要补上载波波长值的1/2,即a2=a2+(λc/2)。

在定位多阅读器中,不能预先做出标签与阅读器间远近程度的判定,货物登记误差的问题往往会在仓储入口应用场景中产生,从而导致重大损失。为了妥善解决此问题需要使用多标签的办法,在此方式下进行定位可通过单阅读器天线来完成,降低硬件设施的成本,本算法的流程图如图3 所示。

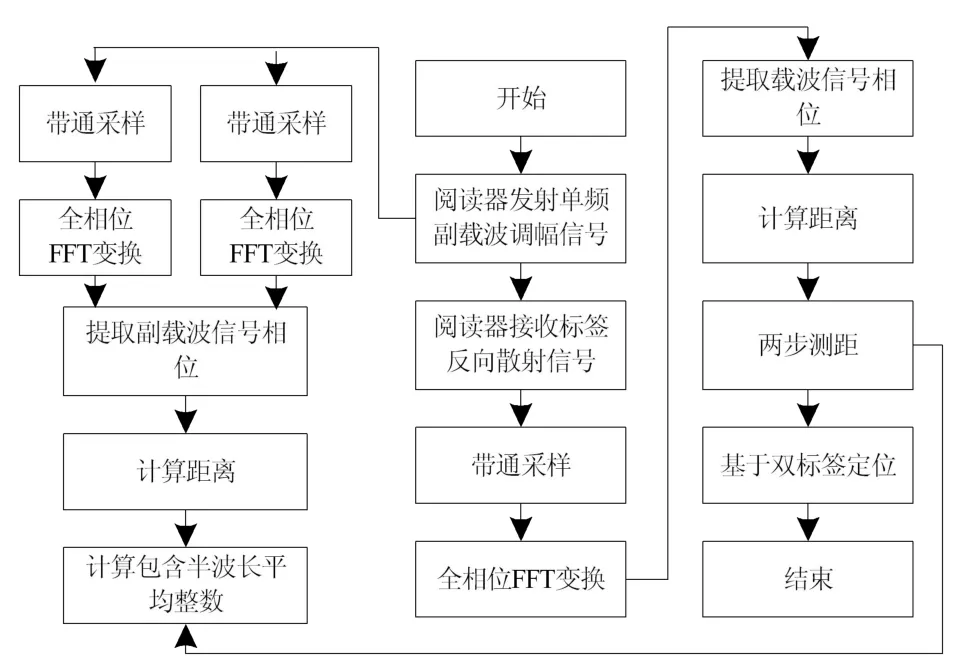
图3 基于双标签的定位方法流程框图

3 仿真结果分析

仿真实验在Matlab 工具软件中进行,仿真场景为一仓储入口,尺寸为4.5 m×8.5 m; 以坐标原点(0,0)作为阅读器天线的位置,假设待定目标的数量是105 个,有2 个标签附着于每个待定位目标上,而且入口中心线是对称的。在y轴方向上,阅读器和待定位目标距离为任意长度; 阅读器副载波频率为2.5 MHz,载波频率为921 MHz,信噪比为10.2 dB,仿真次数为105 次。待定位标签i测距估计值与实际值di,j间的平均测距误差f的计算公式为其中,M为标签数,N为仿真次数。

待定位目标i估计值(xi0,yi0)与实际值(x,y)间的定位均方根误差e的计算公式为

平均定位误差eave的计算公式为其中,Q为待定位目标数。

接下来做如下设想: 有2 种多途径传播路径,分别为两条和三条。其中一条来自墙壁单次反射路径,和另一条视距传播路径组成两条传播路径; 在前面两条的路径上再加一条墙壁双次反射路径,共同组成了3 条传播路径。在直接利用副载波相位估计标签距离Ds后测距部分随之形成,该方法称之为单步测距; 在对估计标签距离时所采用的是两步测距法(载波),这是在双标签的基础上形成的方法; 由公式(3)可知,载波相位计算距离Dc,i可以被副载波相位计算距离ll所替换,以此作为两步测距(副载波),通过比较两步测距(载波)、两步测距(副载波)2 种方法的定位误差后定位部分随之形成; 如何理解两步测距(副载波)、统计两步测距(载波)方法判别率的问题,从其实质来看是对物品是否属于未登记做出判定,这是在待定位目标估计位置的基础上完成的,表3 为3 种测距方法的平均测距误差。

表3 测距误差

由表3 可知,在两条路径条件下,两步测距(载波)方法平均误差为0.210 m; 两步测距(副载波)方法平均误差为0.200 m; 单步测距方法平均误差约为0.322 m; 以两条路径作为前提条件可以确定用这3 种方法都会有测距误差产生,而且差异是相类似的,由此可以做出判断,两步测距法比单步测距法准确性更高,可以减少测距误差。图4 为载波和副载波2 种情况下运用两步测距法产生的误差概率对比。

由图4 可知,在三条路径、两条路径情况下,两步测距(载波)方法最大误差分别为0.92、1.00 m,估计平均定位误差分别为0.55、0.50 m; 在三条路径、两条路径情况下,两步测距(副载波)方法最大误差分别约为0.97、1.00 m,估计平均定位误差分别为0.57、0.54 m; 这表明两步测距(载波)方法对本研究提出的基于双标签的定位方法更加适合。而对于测距误差,两步测距(副载波)方法和两步测距(载波)方法相差虽较小,但在基于双标签的定位中,无法确保阅读器与2 个标签间距离大小关系。货物登记状态误判问题在仓储空间场景中十分重要[12]。在105 次仿真实验中,对105 个待定位目标进行统计。两步测距(载波)分别在三条路径、两条路径的条件下误判率都是0,两步测距(副载波)方法误判率分别为17.45%、17.82%。说这表明两步测距(载波)方法具有较高的准确性,可以降低定位误差,对物品能够做出准确的登记,适用于本次仿真场景[13]。图5 为UHF RFID 阵列天线方位测试场景图。

图5 UHF RFID 阵列天线方位测试场景图

4 结论

伴随着无线定位技术的应用推广,此项技术也由室外逐步扩展到室内,这也让无源UHF RFID 室内定位技术得到广泛的应用,其优势在于无源标签体积较小,因此基于标签室内定位技术引起各界关注而成为研究的重点内容。本文基于单天线相位的UHF RFID,对室内定位算法进行了研究,得出如下结论:

(1)如果待定位目标边长距离要超过高频载波信号波长,有2 个间距附着于待定目标上,此无源标签是载波波长的1/2。处于单阅读器天线的条件下定位阅读器与标签间存在三角几何关系。使用2 个无源标签可以对测距误差进行调整,把定位误差降下来。

(2)仿真表明,在三条路径、两条路径情况下,两步测距(载波)方法最大误差分别为0.92、1.00 m,估计平均定位误差分别为0.55、0.50 m; 两步测距(副载波)方法最大误差分别约为0.97、1.00 m,估计平均定位误差分别为0.57、0.54 m; 但两步测距(副载波)方法基于双标签定位中,无法确保阅读器与2 个标签间距离大小关系。

(3)在三条路径、两条路径情况下,两步测距(副载波)方法误判率分别为17.45%、17.82%,两步测距(载波)方法误判率均为0。因此,两步测距(载波)方法可将定位误差降低,确保物品登记的准确性。