基于材料强度的无背索斜拉桥极限跨径研究

葛 欢 林丽霞

（兰州交通大学土木工程学院，兰州 730070）

0 引言

无背索斜拉桥中倾斜的桥塔和轻盈的主梁具有较好的景观效果，而在城市桥梁中占有一席之地。国内外许多学者对斜拉桥的极限跨径与力学性能开展了一系列的研究。王伯惠［1-2］基于平均索法，从斜拉索的强度、主梁轴力、斜拉索的有效弹性模量以及风动稳定性等角度分析了斜拉桥的极限跨径。李国豪［3］提出将斜拉索视为索膜单元，即斜拉索认为是一个竖直平面内的索膜，实现了将斜拉索作为连续体，避免了斜拉索结构布置的变化。胡阳［4］研究了无背索混合梁钢—混结合段在关键荷载工况下结构设计的安全性与合理性。蔡小杨等［5］通过对柔梁密索体系矮塔斜拉桥和常规斜拉桥的力学行为进行了研究，结果表明，柔梁密索体系下的主梁轴力和斜拉索的索力比常规斜拉桥大。陈恒大等［6］基于钢主梁极限抗拉、抗压强度相等的方法，利用斜拉桥的索膜假定，求解了部分地锚斜拉桥极限跨径，并得到其极限锚跨比。彭义等［7］认为结构的屈曲稳定性是限制自锚式预应力矮塔斜拉桥跨径增大的决定性因素。张杨永［8-9］分别从斜拉索和主梁的材料强度、结构变形、压屈稳定性、风动稳定性的角度探讨了自锚式斜拉桥结构体系的极限跨径。Gimsing［10］从拉索竖向支承效率角度，将扇形式索面布置等效为辐射式索面布置，推算出斜拉桥的极限跨径大约是5 000 m。张新军等［11］从采用多振型地震反应谱方法进行E1地震作用下结构的地震反应分析，揭示了超大跨度部分地锚式斜拉桥地震反应的特性。

无背索斜拉桥随着跨径的增大，斜拉索长度增加，会导致斜拉索的垂度效应更明显，再加上索力非均匀变化，两者共同作用下将导致主梁的轴力出现非线性特征。大量研究资料表明，主梁轴力是限制极限跨径的主要因素［1-2］。然而针对极限跨径的研究大多集中于常规斜拉桥，忽略了在无背索斜拉桥中桥塔倾角和竖向荷载斜拉索自重的影响。本文基于平均索法和索膜法的理论，在材料线弹性范围内进行极限跨径研究。考虑斜塔倾角和斜拉索自重推导主梁轴力表达式，基于主梁截面轴心抗压承载力的要求推导极限跨径表达式，并对表达式中主要的结构参数进行分析，研究结果可对同类型桥梁的设计提供参考。

1 极限跨径公式推导

为了推导公式方便，以扇形式索面布置为例，引入如下假定：

（1）主梁所承受的荷载均等效为均布荷载。在无背索斜拉桥中，恒载占的比重比活载的比重大，并且在公路桥梁中的活荷载主要为车道荷载，故将荷载等效为均布荷载。

（2）拉索在主梁及斜塔上均为等索距布置。在常规斜拉桥中，其索面的布置形式有扇形式、辐射式、竖琴式。其索距在很大一部分斜拉桥中都为等索距布置，因此假设为等索距布置具有研究的一般性。假如斜拉索非等索距布置，需要另行分析，不在本文赘述。

（3）不考虑斜塔纵桥向抗推刚度。常规斜拉桥在不同竖向荷载的作用下，桥塔纵向抗推刚度变化较大，即桥塔结构的纵向抗推刚度和其本身受到的竖向荷载大小有关［12］。在无背索斜拉桥中，由于桥塔具有倾角使得该项影响变小，为简化计算，故不考虑斜塔纵桥向抗推刚度［6］。

（4）不考虑竖向荷载对主梁的弯矩作用。无背索斜拉桥密索体系的主梁以承受轴力为主，弯矩较小［7］，故本文不考虑竖向荷载对主梁的弯矩作用。

1.1 平均索法

平均索法［1］就是将扇形索等效为一根虚拟索，索在塔上的锚固点位于锚固区中心h1/2，在梁上的锚固点位于主梁有索区长度的一半（Ly/2）。结构分析简图如图1所示。

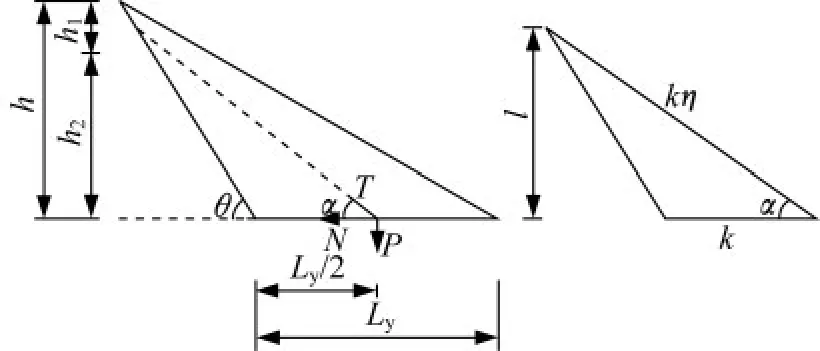
图1 平均索法结构分析简图Fig.1 Structural analysis diagram of average cable method

1.1.1 主梁轴力公式

文献［1］中桥塔θ=90°，无背索斜拉桥桥塔倾角为θ，重新建立公式如下。

斜拉索倾斜度：

式中：h、h1分别为斜塔高度、索塔锚固区一半高度；θ为斜塔倾角；Ly为有索区长度；k1为斜拉索倾斜度。

由图1可知，令

依据等索距布置假设可知：

式中：λ1、λ2分别为主梁索距、斜塔索距；n为索距的个数；μ为索距比，μ=λ1/λ2。

将式（4）代入式（2）得到：

由荷载平衡理论，即每根拉索仅承担索距范围内的恒活载和一半的斜拉索自重。可知主梁承受的竖向荷载P为

式中：Pd为一期恒载；Pm为二期恒载；Pq为活载（汽车荷载、人群荷载）；Pt为斜拉索自重；λ为一根斜拉索计算结果与整体分析结果差值的增大系数，一般可取1.10～1.15。

式中：AT为斜拉索面积；γT为斜拉索容重；LT为拉索平均索长。

平均索的索力值T：

斜拉索对主梁产生的轴力N为

由式（10）可知，用平均索法计算的主梁轴力与与荷载、斜塔倾角、主跨跨径、斜塔高度及塔梁索距比有关。

当θ=90°时，主梁轴力N为

式（11）与文献［1］中的公式具有一致性，而式（11）为式（10）的特殊情形，故说明了式（10）的正确性。

1.1.2 极限跨径公式

主梁承受的弯矩作用对极限跨径的影响比轴力作用时的影响小，故忽略竖向荷载对主梁的弯矩作用。基于主梁截面轴心抗压承载力的要求，主梁承受的轴力为

式中：ε为主梁截面面积增大系数；Am为主梁截面面积；［σm］为主梁材料容许应力。

将式（12）代入式（10）得到极限跨径表达式：

因为主梁恒载包括一期恒载（主梁自重）以及二期恒载（护栏、桥面铺装等），即

式中，γm为主梁容重。

将式（14）代入式（13）可得主梁截面面积与极限跨径的关系式：

1.2 索膜法

索膜法［3］是将斜拉索索面等效为竖直平面内的索膜，当作连续体分析，索距长度为Ly。结构分析简图见图2。

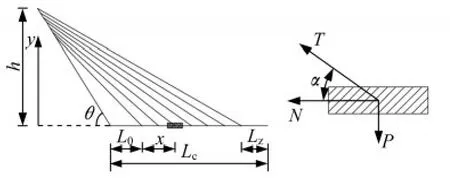
图2 索膜法结构分析简图Fig.2 Structural analysis diagram of cable-membrane method

1.2.1 主梁轴力公式

由主梁有索区微段平衡条件：

式中：L0为塔根无索区长度；x为主梁有索区段长度；y为斜塔有索区段高度。

根据等索距布置假设：

式中，λ1、λ2分别为主梁索距、斜塔索距。

由几何关系得到拉索在主塔上的布置位置方程为

式中，φ=μsinθ。

将式（18）代入式（16）进行积分，积分区间为［x，Ly］。

解得主梁轴力为

主梁承受竖向荷载P为

式中，α为斜拉索倾角。

由式（19）、式（20）可知，用索膜法计算的主梁轴力与与荷载、斜塔倾角、斜拉索倾角、主跨跨径、斜塔高度及塔梁索距比有关。

当θ=90°时，主梁轴力N公式：

式（21）与文献［8］中的公式具有一致性，而式（21）为式（19）的特殊情形，故说明了式（19）的正确性。

1.2.2 极限跨径公式

主梁承受的弯矩作用对极限跨径的影响比轴力作用时的影响小，故忽略竖向荷载对主梁的弯矩作用。基于主梁截面轴心抗压承载力的要求，主梁承受的轴力N为

将式（22）代入式（19）可以得到极限跨径表达式：

2 关于极限跨径的讨论

2.1 仅考虑结构自重作用下的极限跨径

结构仅在自重作用下，材料达到容许应力，此时可以得到跨径的最大值。主梁承受竖向荷载P为

将式（24）代入式（15）可以得到极限跨径随主梁截面面积的变化曲线（图3）。

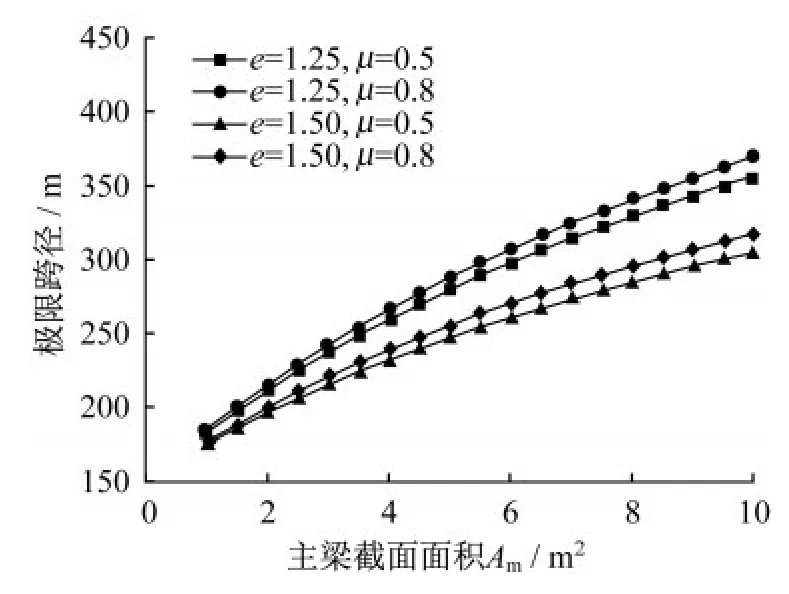
图3 主梁横截面面积与跨径的关系曲线Fig.3 Relationship curve between cross-sectional area and span of main girder

由图3可知：

（1）Am-Ly曲线的切线斜率随主梁截面面积而变化，Am越大，跨径越长，但是当Am=10 m2左右时，极限跨径达到350 m时，趋于平缓。

（2）当高跨比e从1.5 减小到1.25 时，极限跨径增加1/3左右。

（3）当索距比μ从0.5 增加到0.8 时，极限跨径增加5%左右。

2.2 考虑恒载及活载作用下的极限跨径

上述的研究忽略了二期恒载Pm和活载Pq的影响，给出了只承受结构自重情况下的极限跨径，是极限跨径的上限。为考虑桥梁结构在实际状态下的受力情况，下面研究二期恒载和活载对极限跨径的影响。用等效活载来考虑活载作用，恒活载比为4［6］。令Pm+Pq＝αAmγm，其中α为恒活载比。此时荷载P为

将式（25）代入式（23）可以得到极限跨径随恒活载比的变化曲线（图4）。

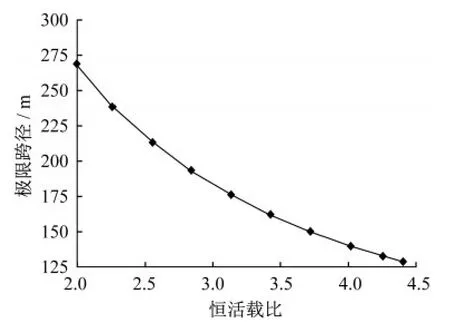
图4 极限跨径随恒活载比的变化曲线Fig.4 Variation curve of ultimate span with dead load to live load ratio

由图4可知：

（1）极限跨径随恒活载比值α增大而迅速降低，在桥梁结构的设计中，活载是由通行要求确定的，此时需降低恒载的大小，比如尽可能采用轻质高强的高性能混凝土、轻型护栏以及减小铺装层厚度、主梁横截面面积等措施来进一步增大极限跨径。

（2）当恒活载比为2左右时，无背索斜拉桥跨径最大可以达到270 m。

3 算例分析

为验证本文所推导的极限跨径表达式的正确性，建立无背索斜拉桥的有限元模型（图5），并与平均索法和索膜法计算的关键截面处的轴力进行对比分析。

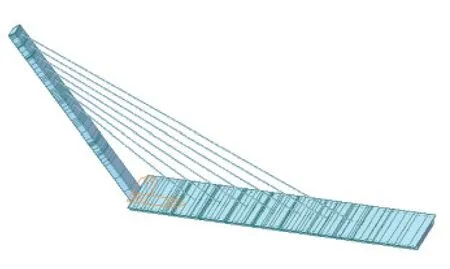
图5 无背索斜拉桥有限元模型Fig.5 Finite element model of cable-stayed bridge without back cable

有限元模型共171 个节点、100 个单元；主梁截面为单箱三室截面，斜塔截面为实腹八角形截面，主梁和斜塔均为梁单元；斜拉索为桁架单元，与斜塔、主梁为刚性连接，结构体系为塔梁墩三者固结。计算所用荷载集度见表1，主要结构参数见表2，材料特性见表3，计算结果及误差见表4和图6。

表1 荷载集度Table 1 Load concentration kN/m

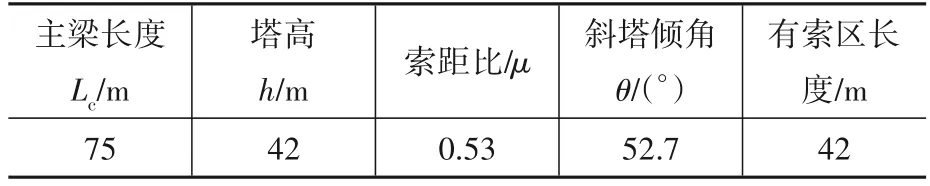
表2 主要结构参数Table 2 Main structural parameters

表3 材料特性Table 3 Material properties

表4 关键截面主梁轴力计算结果与误差Table 4 Calculation results and errors of axial forces at key sections of main girder

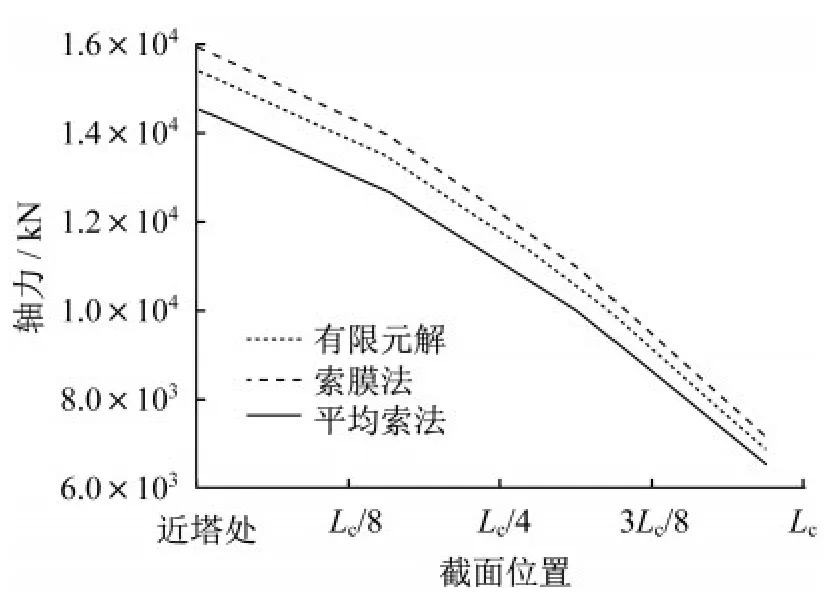
图6 扇形式主梁轴力曲线Fig.6 Axial force curve of fan-shaped main girder

由图6可知，索膜法和平均索法与有限元计算结果吻合，其中索膜法是更偏于安全的计算方法。

由表4 可知，平均索法推导的主梁轴力公式与有限元结果之间的误差在7%以内，索膜法与有限元结果之间的误差在5%以内。

当考虑竖向荷载对主梁的弯矩作用时，主梁上、下缘弯曲应力增加，最终导致无背索斜拉桥的极限跨径减小。

本文仅考虑材料强度下无背索斜拉桥极限跨径的表达式，并未考虑变形、抗风、抗震等因素。若考虑主梁的变形，随着斜拉桥跨径的增大，活载作用下主梁挠度迅速增加。当竖向挠度按Lc/400控制时，极限跨径随着主梁上索距的减小而迅速增大；随着梁塔索距比和索塔高跨比的增大而增大［2］。若考虑抗风稳定性，斜拉桥的极限跨径随设计基准风速的增大而减小；随桥面系单位长度质量的增大而增大［9］。若考虑地震作用，随着地锚段主梁长度增大，主塔在地震作用下纵向位移明显增大，主梁产生较大的纵向位移，而且随着斜拉索竖向支承刚度的增强，主梁的竖向位移明显减小［11］。

4 结论

（1）基于平均索法和索膜法，考虑斜塔倾角以及斜拉索自重的影响，推导了无背索斜拉桥的主梁轴力公式，在本文所考虑的运营情况下，基于截面轴心抗压承载力的要求，无背索斜拉桥的极限跨径最大可以达到270 m。

（2）从推导出的极限跨径表达式当中可以看出，极限跨径的大小与高跨比、索距比、主梁截面面积等参数有关；当高跨比从1.5 减小到1.25 时，极限跨径增加1/3左右；当索距比从0.5增加到0.8时，极限跨径增加5%左右；当主梁截面面积达到10 m2，自重作用下的极限跨径上限可以达到350 m。

（3）通过算例分析，平均索法与有限元结果相差7%，索膜法与有限元结果相差5%，两种计算方法与有限元结果的误差均远小于10%。说明两种方法均可适用于求解主梁轴力，并基于此推算出极限跨径，索膜法更偏于安全。本文极限跨径计算方法可为同类桥梁设计提供参考。