简支钢混组合梁新型桥面连续结构的力学性能参数分析

王清泉 曹 沛 邓青儿

（同济大学建筑设计研究院（集团）有限公司，上海 200092）

0 引言

简支梁具有经济效益好、构造简单、受力明确、施工速度快等优点，在我国近现代桥梁建设中占有重要席位。但是简支梁伸缩缝多，降低了桥面的平整性，车辆在伸缩缝处易出现“跳车”现象，严重影响行车速度、安全和舒适性。此外，伸缩缝长期承受汽车动载，易损坏，养护困难，需要经常更换。

为了解决上述问题，20 世纪70 年代末，工程师提出了桥面连续的概念，即将相邻两跨简支梁桥面板（全部或部分）或桥面铺装连成一体代替伸缩缝构造，这样一来既能继续利用简支梁的优点，又能提高桥面平整性。80 年代日本开始大规模采用桥梁无缝化技术来避免伸缩缝装置的弊端，其中桥面连续是最经济可行的方式之一，通过选择合适的桥面连续材料或设置人工缝来吸收、分散或诱导桥面连续的变形［1］。目前国内大量空心板梁、T 梁及小箱梁等中小跨径桥梁都采用了桥面连续构造［2-3］。桥面连续构造根据受力方式和施工工艺不同，分为铰接式、刚接式和拉杆式。大量工程实践表明，这样的桥面连续结构由于结构厚度小，整体性差，配筋少，很多情况下无法满足受力要求，导致连续结构开裂、渗水，耐久性较差，增加了养护成本。

随着组合梁的发展，桥面连续运用于组合桥梁的工程实例也逐渐增多。简支组合梁的桥面连续典型结构是以无粘结桥面连续DLS（Debond Link Slab）［4-6］为主，率先在欧美国家兴起，主要处理方式是将桥面连续构造作为桥面板的一部分进行设计，但DLS施工时需要浇筑母板，且破坏后容易导致钢梁上翼缘腐蚀。

1 新型桥面连续结构

1.1 新型桥面连续结构简介

笔者结合既存桥面连续结构的优缺点，以“构造简单、受力可靠、经济可行、耐久性好”为出发点提出了一种新型桥面连续结构，如图1所示。

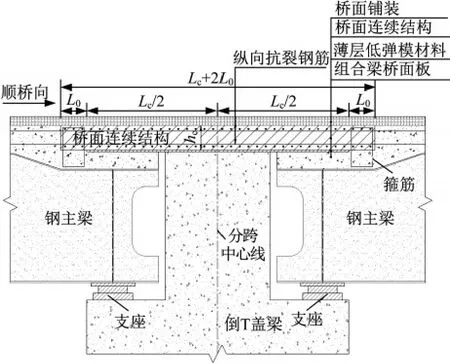
图1 桥面连续构造示意图Fig.1 Schematic of deck continous structure

在简支组合梁端部设置桥面连续结构。其无粘结长度为Lc，板厚为hc，在无粘结长度范围内设置薄层低弹模材料。在桥面连续结构内设置纵向抗裂钢筋，在桥面连续结构端部设置长度L0的过渡段，过渡段内设置箍筋或加长剪力钉，确保桥面连续结构端部与组合梁桥面板之间可靠连接和刚度匀顺过渡。组合梁端部通过下凹钢主梁来确保组合梁桥面板具有需要的厚度，以提供足够的端横梁横向刚度，并为后浇的桥面连续结构混凝土提供模板，同时保证运营阶段桥面连续结构开裂后钢梁的耐腐蚀性。

1.2 新型桥面连续结构受力分析

以下对本新型桥面连续结构在主要荷载作用下的受力模式进行简要的分析。

1.2.1 纵向位移作用下桥面连续结构受力分析

桥面连续结构在汽车制动力及整体温度作用下，组合梁会产生整体纵向变形使得桥面连续结构产生纵向拉伸或者压缩作用，其中纵向拉伸会导致桥面连续结构混凝土受拉开裂，如图2所示。

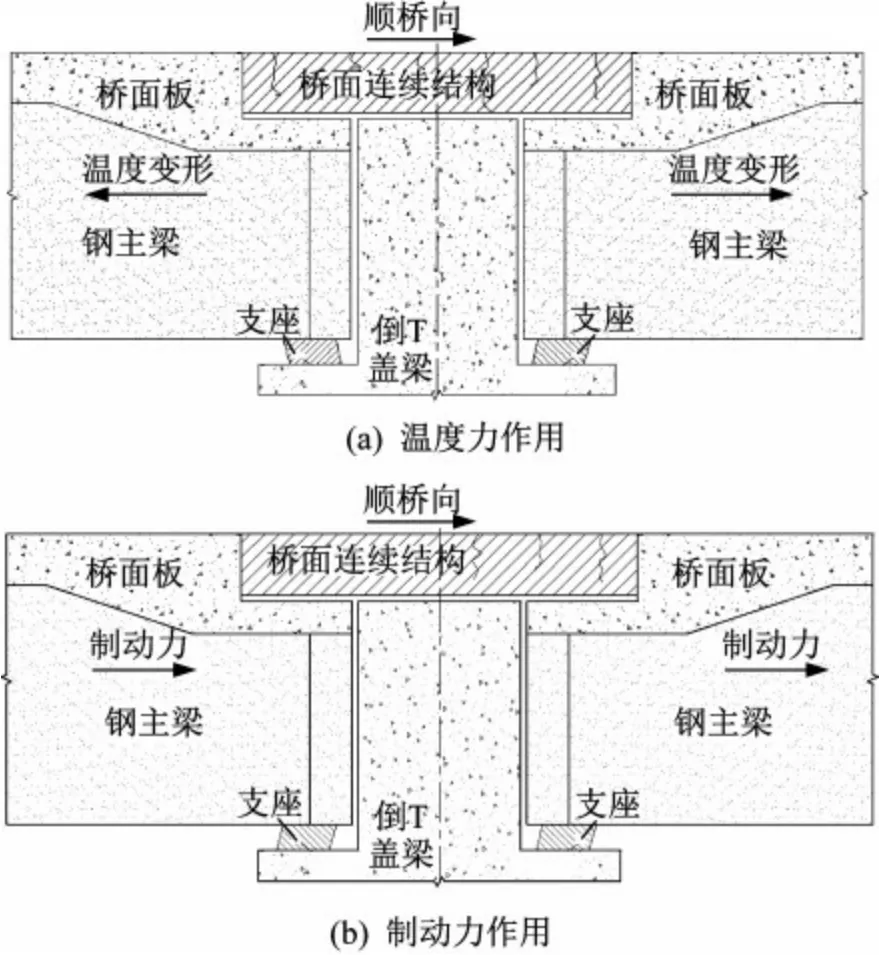
图2 纵向位移下桥面连续结构变形状态Fig.2 Deformation state of continuous deck structure under longitudinal displacement

1.2.2 梁端转动下桥面连续结构受力分析

在恒载、收缩徐变、梯度温度（混凝土桥面板和钢主梁因膨胀系数不同导致变形差）、车道荷载及不均匀沉降等作用下，简支组合梁端部产生转动使桥面连续结构承受负弯矩而导致上表面开裂。其中，当结构及作用对称时，组合梁端部转角一致，则会产生如图3 所示变形状态，反之，则会产生如图4 所示变形情况。此时桥面连续结构主要承受弯矩，上翼缘受拉，下翼缘受压。

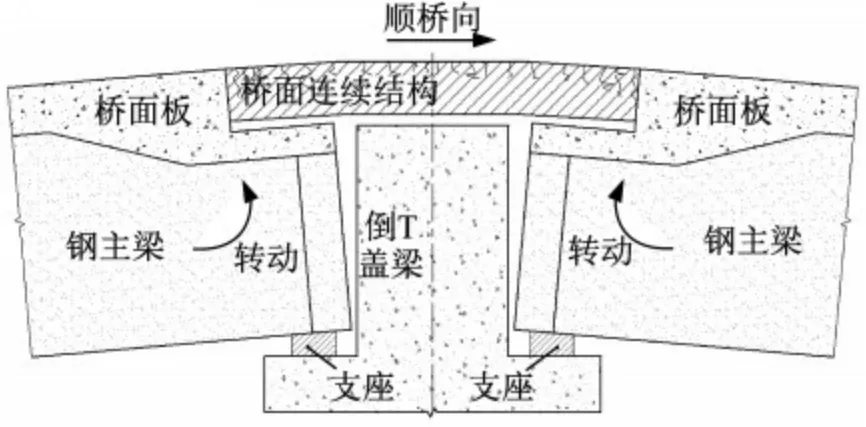
图3 对称转角下的桥面连续结构变形状态Fig.3 Deformation state of continuous deck structure under symmetric rotation

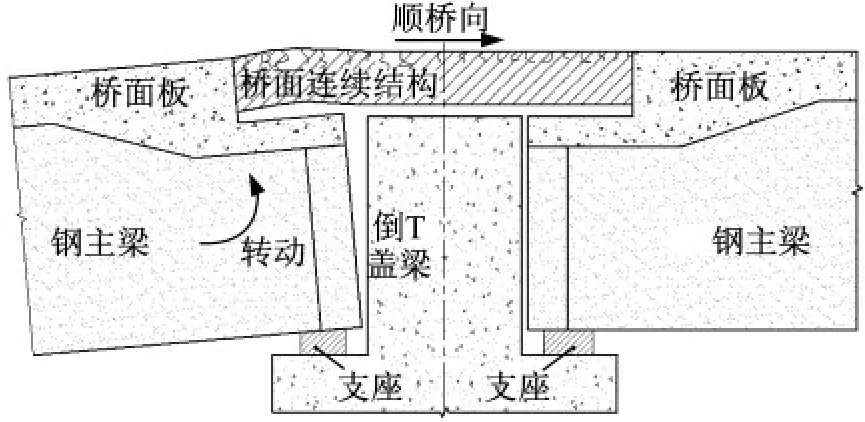
图4 非对称转角下的桥面连续结构变形状态Fig.4 Deformation state of continuous deck structure under asymmetric rotation

2.2.3 局部轮载作用下桥面连续结构受力理论分析

当桥面连续结构下方为非刚性支承时（脱空或者弹性支承），车轮荷载作用下桥面连续结构为两端固结梁的受力模式。当车轮作用在桥面连续结构跨中时，桥面连续结构跨中下表面及端部上表面承受拉应力而开裂，如图5所示。

图5 局部轮载下桥面连续结构变形状态Fig.5 Deformation state of continuous deck structure under local wheel load

综上可知，在恒载、收缩徐变、车道荷载、梯度降温、整体升温、支座沉降等作用下，桥面连续结构会因为轴向变形、梁端转动而承受轴拉力及负弯矩，导致表面开裂，因此需要进行必要的结构设计来确保其具有足够的抵抗外力能力，控制裂缝发展。

2 新型桥面连续结构计算模型

2.1 计算条件

现以匹配倒T 盖梁的4×35 m 简支钢混组合槽梁为研究对象，分析该新型桥面连续结构受力性能及主要影响参数。单跨简支梁梁长35 m，计算跨径为32.44 m，桥宽取6.45 m，构造及尺寸如图6所示，支座布置如图7所示。

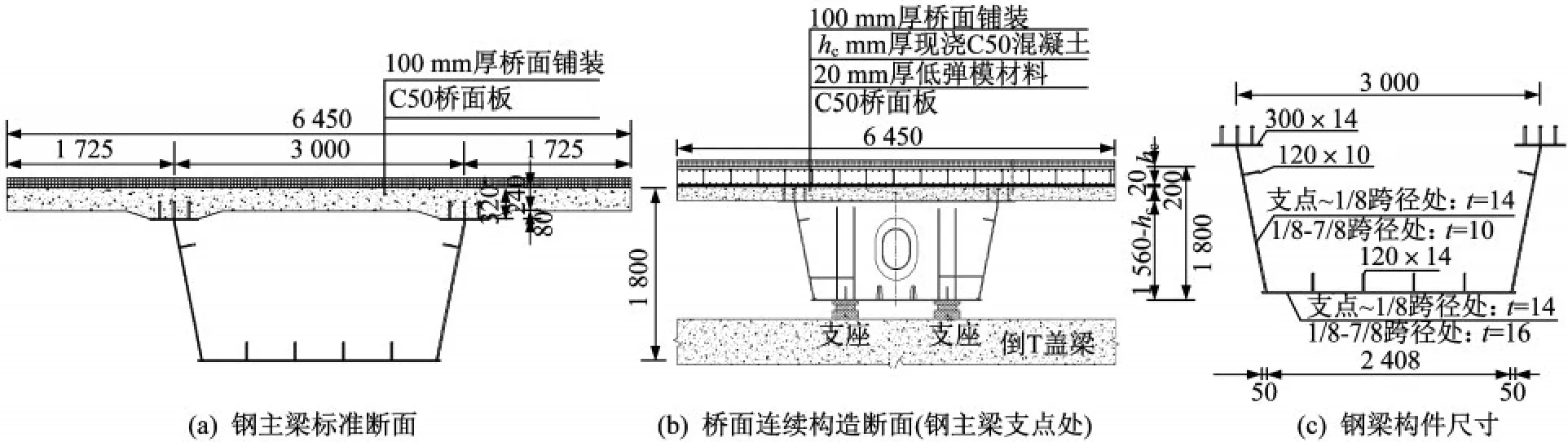
图6 简支钢-混组合梁断面布置图Fig.6 Cross-section of simply supported steel-concrete composite beam bridge

图7 支座布置图及刚度取值Fig.7 Schematic of bearing layout and stiffness value

桥面连续结构分析时考虑的作用如表1所示。

表1 作用取值Table 1 Action Values

进行桥面连续结构设计时主要考虑承载能力极限状态（基本组合）及正常使用极限状态（频域及准永久组合）验算。各作用组合的作用分项系数取值如表2所示。

新型简支-桥面连续钢混组合梁施工过程如下：

（1）架设组合梁。钢主梁自重及桥面板自重由简支组合梁体系承担。

（2）施工栏杆。栏杆重量由简支组合梁体系承担。

（3）施工桥面连续结构后施工铺装。桥面连续结构湿重及铺装由简支-桥面连续体系承担。

2.2 计算模型

采用Midas Civil 2020 建立梁单元模型进行分析。组合梁采用双单元模拟（混凝土桥面板+钢主梁），单元间距1～1.5 m，不考虑桥面板与钢主梁之间的滑移效应，二者之间采用刚性弹簧单元连接；桥面连续结构处采用三单元模拟（桥面连续结构+混凝土桥面板+钢主梁），单元间距0.1～0.15 m，桥面连续结构与组合梁之间采用仅受压弹簧单元连接，可调节竖向支承刚度，水平向刚度为零，如图8所示。

图8 分析模型Fig.8 Schematic of analysis model

3 桥面连续结构受力影响参数分析

通过2.2节的简要分析可知，不同荷载作用下的新型桥面连续结构受力形态各异。桥面连续结构受力与其约束情况（即主梁对桥面连续结构的支承情况，主要指二者之间无粘结段长度LC范围内的填充物所能提供给桥面连续结构的竖向支承刚度）、无粘结段长度及桥面板厚度相关。现逐一对以上影响因素进行分析。

3.1 桥面连续结构与主梁间的竖向支承刚度

以无粘结长度Lc=4 m、板厚hc=280 mm 的桥面连续结构为研究对象，采用仅受压弹簧单元模拟桥面连续结构与组合梁之间的竖向支承，其竖向刚度在0～107kN/m 之间变化（即脱空到刚性支承变化），得到如图9 所示的桥面连续结构弯矩及轴力（除特殊说明外，各内力图均取基本组合包络最大值，下文同）与竖向支承刚度关系图。

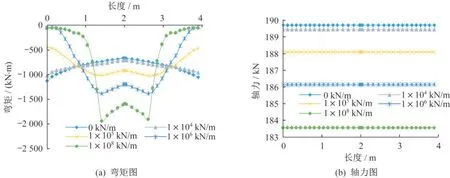
图9 不同竖向支承刚度下的桥面连续结构内力图Fig.9 Stress state of continuous deck structure with different vertical bearing stiffnesses

由图可知，①随着桥面连续结构与组合梁之间竖向支承刚度的变化，桥面连续结构的受力模式逐渐发生改变。随着竖向支承刚度的增加，桥面连续结构端部弯矩逐渐降低，跨中弯矩逐渐增大，变化拐点出现在桥面连续结构约1/4Lc处。②桥面连续结构轴力随竖向支承刚度增加而增加，但变化不大。总体来看，桥面连续结构以承受负弯矩为主，轴向受力较小，因此后续参数分析中仅针对弯矩项进行。

现将以上竖向支承刚度下桥面连续结构承担的基本组合下最大弯矩值汇总如表3所示。

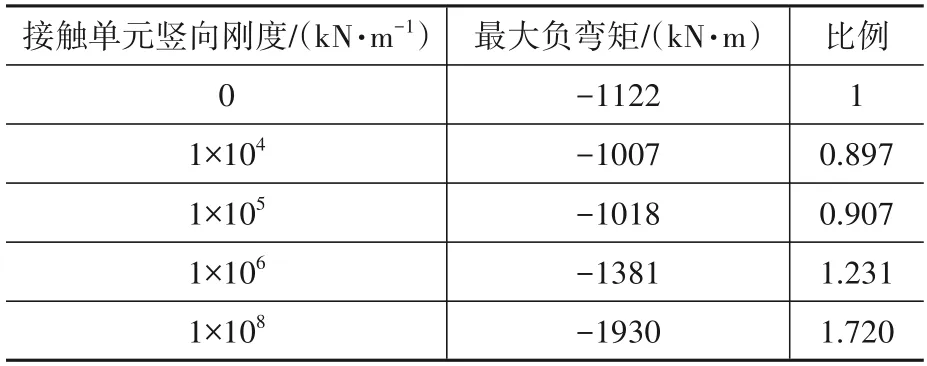
表3 不同竖向支承刚度下的桥面连续结构最大弯矩表Table3 Maximum moment of continuous deck structure with different vertical bearing stiffnesses

由表3 可知，①当桥面连续结构与组合梁之间脱空时，桥面连续结构端部承担的最大弯矩为1 122 kN·m；当桥面连接结构刚性支承于组合梁上时，在组合梁端部位置处的桥面连续结构所承担的弯矩最大，达到1 930 kN·m，较支座脱空时增加了72%，说明桥面连续结构不宜刚性支承于组合梁上。②通过调节桥面连续结构与组合梁之间的竖向支承刚度可以改变桥面连续结构的受力模式。当竖向支承刚度在104kN/m 左右时，桥面连续结构弯矩较脱空状态可降低约10%。③弹性支承与脱空条件相比对桥面连续结构受力改善幅度有限。进一步分析可知，随着桥面连续结构无粘结长度的减小，上述改善边际效应更小。

考虑到弹性支承时需采用边界非线性方法进行分析，对于工程设计而言过于复杂。此外，寻找合适的弹性支承材料及其施工均有难度，且弹性材料容易老化失效，因此考虑桥面连续结构与主梁之间脱空来进行结构设计更为简便有效。

3.2 无粘结长度

考虑桥面连续结构竖向脱空，桥面连续结构板厚度取280 mm，研究无粘结长度2～6 m 下桥面连续结构受力情况。以边跨与次边跨之间的桥面连续结构为例进行分析。不同荷载作用下桥面连续结构弯矩如图10所示。

图10 各项荷载作用下不同无粘结长度的桥面连续结构弯矩图Fig.10 Moments of continuous deck structure with different unbonded lengths under various loads

由图10 可知，①在上述各项荷载作用下，桥面连续结构端部受力均大于跨中受力，基本组合作用下桥面连续结构主要承担负弯矩，结构上表面受拉，下表面受压。②恒载及车道荷载作用下，桥面连续结构端部弯矩随着无粘结长度增加先降低后反向增加，拐点出现在无粘结长度为3～4 m时（即为相邻跨径之和的5%左右）；跨中弯矩随无粘结长度增加而降低。当无粘结长度较小时，梁端转动对桥面连续结构受力影响起主导作用；当无粘结长度增加到一定程度后，由于无粘结段在自身恒载及车轮集中力作用下的效应明显，导致端部负弯矩增加幅度较大。③收缩徐变、温度及沉降作用下，桥面连续结构整体弯矩随着无粘结长度的增加而减小，变化幅度与无粘结长度近似呈线性关系。④不同无粘结长度下的桥面连续结构受力中，恒载、车道及温度起主导作用，三者占到总体受力的80%～95%，其中，恒载作用占总体受力的10%～25%，随无粘结长度增加而增大，主要是跨径增大后其自重作用效应比重加大；车道作用占总体受力的45%～55%；温度作用占总体受力的15%～20%。

经分析得知：桥面连续结构承载能力不控制设计，以下仅对抗裂计算结果进行分析。桥面连续结构上表面采用束筋ϕ28 mm@150 mm，下表面采用单层配筋ϕ28 mm@150 mm，得到不同板厚的桥面连续结构裂缝宽度，如表 4所示。

由表4 可知，无粘结长度并非越长越好。从受力角度来看，无粘结长度Lc取3～4 m 为宜（即为相邻跨径之和的5%左右），此时桥面连续结构端部的弯矩及裂缝宽度相对较小。继续增加无粘结长度无任何实际意义。但工程设计中，特别是城市高架桥梁建设，考虑到环保、噪音污染等因素，常常不希望混凝土现场浇筑量过多，一般无法做到5%相邻跨径之和的无粘结长度，因此也可考虑适当减小无粘结长度，适度增加配筋的方式来设计桥面连续结构。

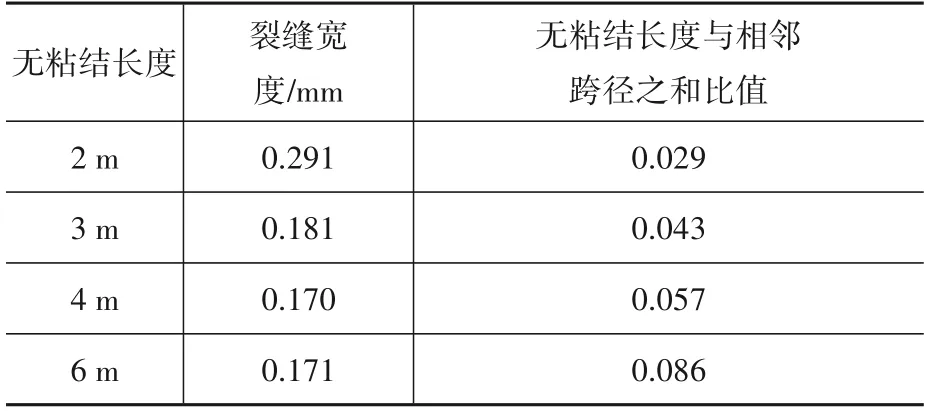
表4 不同无粘结长度下桥面连续结构的裂缝宽度Table 4 Crack widths of continuous deck structure with different unbonded lengths

3.3 桥面板厚度

考虑桥面连续结构竖向脱空，无粘结长度取3 m 及4 m，分析对比板厚200～320 mm 时桥面连续结构的受力情况。以无粘结长度为4 m 时的边跨与次边跨间的桥面连续结构为例，不同荷载作用下桥面连续结构弯矩如图11所示。

由图11 可知，不同荷载作用下，桥面连续结构承受的弯矩随板厚的增加而增加。对不同板厚的桥面连续结构进行抗裂计算，桥面连续结构上表面采用束筋ϕ28 mm@150 mm，下表面采用单层配筋ϕ28 mm@150 mm，得到不同板厚下桥面连续结构裂缝宽度，如表5所示。

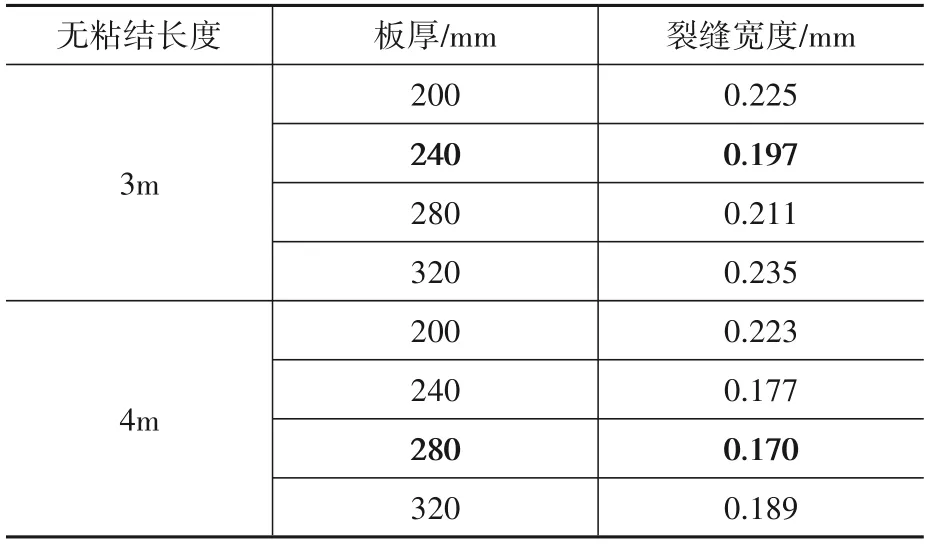
表5 不同板厚下桥面连续结构的裂缝宽度Table5 Crack widths of continuous deck structure with different thicknesses

对比表5 中裂缝宽度数据可知，①通过增加桥面连续结构厚度可有效提高桥面连续结构的抗裂性，但桥面连续结构板厚也有合理取值，当超过一定程度后，桥面连续结构受力增加的幅度大于自身抗力反而对其抗裂计算不利；②无粘结长度不同，匹配的合理桥面连续结构板厚不同，因此在工程实际时需要针对不同无粘结长度桥面连续结构进行合理板厚分析，以便得到最优组合。以本算例为例，当桥面连续结构无粘结长度取3 m 时，对应厚度取240 mm为最佳组合；当桥面连续结构无粘结长度取4 m时，对应厚度取280 mm为最佳组合。

4 桥面连续结构对简支组合梁整体受力的影响分析

以35 m 简支组合梁及4×35 m 简支-桥面连续组合梁为例，取桥面连续结构无粘结长度2～6 m、板厚280 mm，分析简支-桥面连续结构体系的受力与简支结构体系的受力差距，从而判断桥面连续结构的设置对简支组合梁的影响程度。图12为不同无粘结长度下的简支组合梁在跨中位置的作用效应图（其中，无粘结长度为0 表示桥面不连续）。

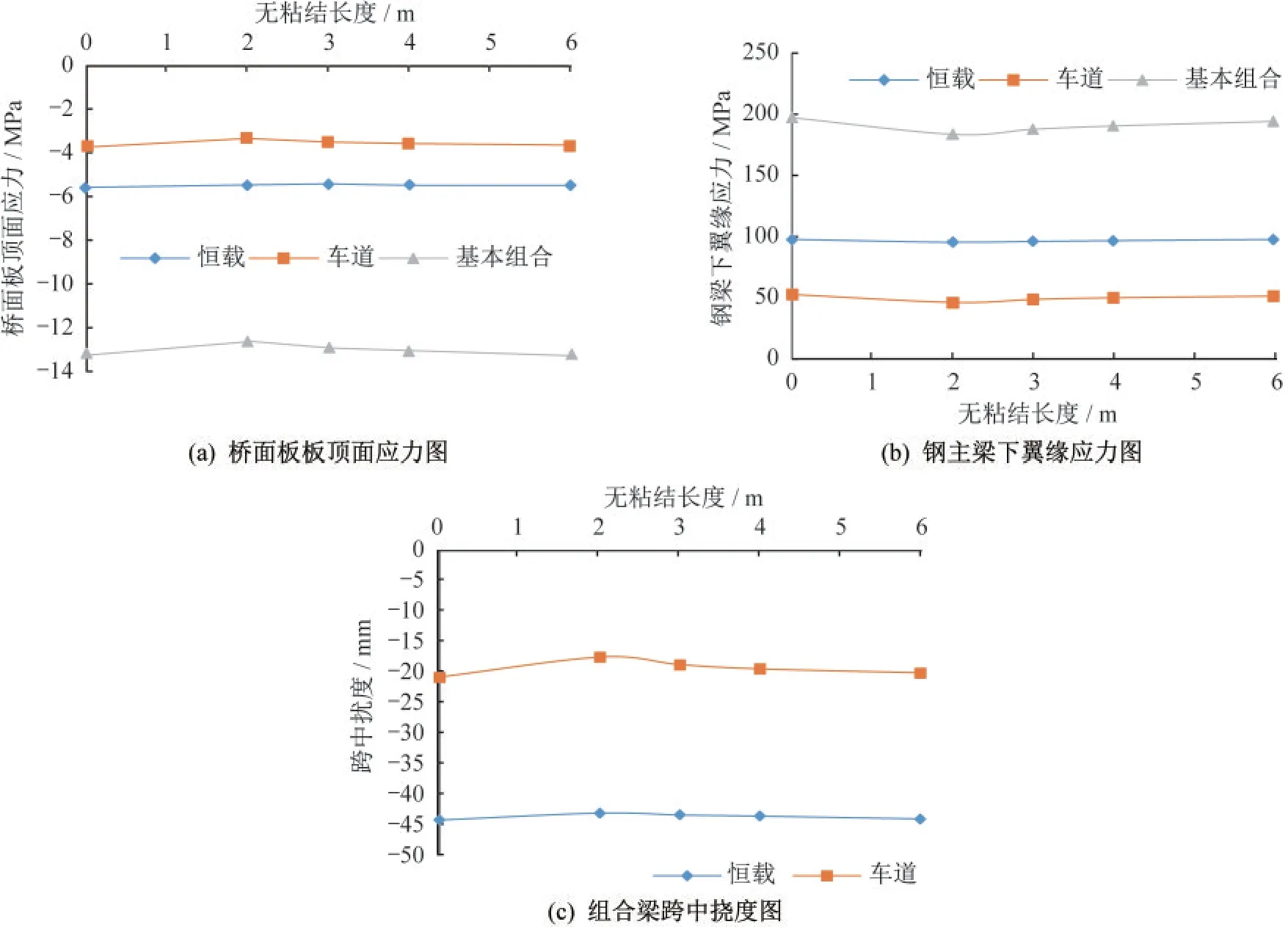
图12 不同桥面连续结构对简支组合梁影响Fig.12 Effects of different continuous deck structures on simply supported composite girders

分析图12 及表6 可知，无论是从受力角度还是变形角度来看，当无粘结长度小于4 m 时（即为相邻跨径之和的5%以下），设置桥面连续结构后对简支梁的跨中受力起到了卸载作用，提高了结构整体性，使得组合梁桥面板顶应力及钢主梁底应力降低了2%～5%，活载变形减小了7%～16%。但随着无粘结长度的增加，桥面连续结构适应变形能力增强，其约束作用降低，对简支梁受力影响变小。本算例中，当无粘结长度到6 m 时，设置桥面连续结构与否对简支梁受力已基本无影响。但总体来看，合理无粘结长度范围内的桥面连续结构对简支组合梁受力影响均较小，简支组合梁整体设计时可不考虑桥面连续结构的影响。

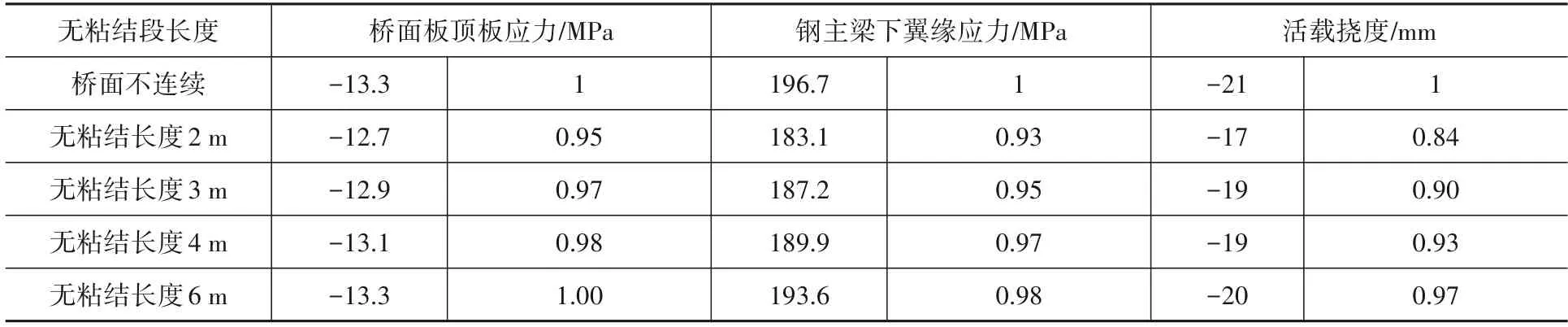
表6 不同无粘结长度下的简支组合梁跨中效应Table 6 Mid-span effect of simply supported composite beams with different unbonded lengths

5 结论

本文提出了一种新型桥面连续结构，旨在克服传统桥面连续结构的弊病，让桥面连续结构更简单、受力更可靠、耐久性更好、经济性更佳，具有较强的工程推广应用价值。笔者对该新型桥面连续结构进行了杆系简化模型计算分析，得到了如下主要结论：

（1）桥面连续结构与主梁之间的竖向支承刚度对其受力模式影响较大。两者之间刚性接触时，在组合梁梁端与桥面连续结构接触位置会产生较大的集中弯矩；通过调节竖向支承刚度可以适当优化桥面连续结构的受力，但从作用组合效应结果来看，效用有限，建议桥面连续结构设计时采用脱空进行。

（2）无粘结长度是影响桥面连续结构受力的重要因素。随着无粘结长度的增加，桥面连续结构的受力先降低后增加，说明无粘结长度并非越长越好。从受力角度来看，无粘结长度取相邻跨径之和的5%左右较为适宜，但综合考虑工程实际，可适当提高配筋率减小无粘结长度以降低混凝土的现场浇筑量，提高施工综合效益。

（3）控制其他变量相同，桥面连续结构受力随着其板厚的增加而增大。结合钢筋混凝土构件抗裂计算可知，找到桥面板连续结构受力与抗力平衡，是其设计的关键所在。以35 m 跨径典型中小跨径简支组合梁为例，当桥面连续结构无粘结长度取3 m 时，对应厚度取240 mm 为最佳组合；当桥面连续结构无粘结长度取4 m 时，对应厚度取280 mm为最佳组合。

（4）桥面连续结构设置与否对简支梁整体受力影响有限，简支梁整体设计时可不考虑桥面连续结构的影响。

（5）本文通过参数分析论证了可以通过选择合理的构造尺寸、加强配筋的方式来设计中小跨径的桥面连续结构，从而使其裂缝宽度控制在工程允许范围内。需要注意的是，本文未对桥面连续结构进行实体分析和试验研究，对其空间受力模式、疲劳性能和具体的设计方法等缺乏数据支撑，这些研究工作将在今后陆续开展。