数据驱动的复杂电网故障区域定位方法研究

杨康， 武家森

（1.国网河南省电力公司郑州航空港经济综合实验区供电公司，河南 郑州 450000；2.北京中恒博瑞数字电力科技有限公司，北京 100085）

在“双碳”目标的引导下，国内外大力发展智能电网技术，电网结构愈加复杂，电网的运行数据量也呈现几何级增长，明显具有大数据特征［1］。大数据技术在智能电网中的应用成为国内外研究热点，亟需研究应用数据驱动技术提高系统稳定运行方法［2-3］。如何能在既保证低难度搭建智能电网模型，又能更加准确高效地对系统故障进行定位已成为亟待解决的问题。目前，国内外学者针对电网故障区域定位方法的研究已经取得了不少成果，传统的故障区域定位方法主要是根据电压的特征数据判断故障相对于电能质量监测装置的位置，从而确定故障所存在的大体区域。文献［4］针对暂态扰动变量波形，对比其近似度确定短路位置。文献［5］通过建立新型算法构造矩阵，确定故障源的可能发生区域。文献［6］利用观测点可测区域、故障节点位置等判据实现定位。上述方法受天气、测量装置等多种因素影响会产生误差较大、定位不准确等问题。因此，如何快速、准确地诊断电力系统故障是运行人员最关心的问题之一［7］。

大数据技术是近年来引起广泛关注的一项新技术。它是指能够高速捕获、发现和分析类型复杂、来源复杂的大量数据，并通过经济方法提取其价值的技术系统［8］。随机矩阵理论（Random Matrix Theory，RMT），通过对线性特征值统计分析，揭示实际数据特征，是数据挖掘技术的典型应用；作为一种数据驱动方法，无需建立特定的机理建模［9-10］。因此，RMT 具有对不同电力系统分析适用性、及时性等特点［11］。文献［12］提出了一种基于传统同步相量法的故障区域检测方法，该方法仅适用于系统故障信号较强时。文献［13］采用谱分布概率密度函数的相似度作为状态评价的判据。通过使用连续、离散小波变换分析瞬态电压波形确定故障区域［14-15］。文献［16］通过建立增广矩阵，将平均谱半径作为评估指标，分析了不同影响因素与评估指标之间的内在关系。由于增广矩阵包含两个或多个矩阵之间的统计信息，故可以广泛应用于电力系统中。

针对上述确定故障区域方法的不足，本文提出基于RMT 和数据驱动的复杂电网故障区域确定方法研究。利用单环定理（single ring theory，SRL）对数据进行分析，提出以平均谱半径（mean spectral radius，MSR）作为相关分析指标确定故障区域。利用IEEE 39 节点系统仿真数据进行了算例验证，结果表明该方法能够确定系统中故障发生的区域。

1 随机矩阵理论

随机矩阵理论是一种以统计学为基础的大数据分析方法。通过建立高维随机矩阵模型，将电网运行数据进行矩阵变换，可以准确高效地处理智能电网中复杂的多层级数据，利用数据特征映射复杂系统的状态。将采样点的时变数据视为随机变量，在系统受小扰动、白噪声或测量误差影响时，采样数据会表现出统计特性，因此可以用合适的指标来描述。当系统中存在事件／信号源时，系统中随机变量的统计特性随着内部运行机制变化而变化。在实际系统运行中，数据的维数会表现出不确定性。但是随机矩阵的某些特征仍然收敛，并具有一定的精度，这表明随机矩阵理论能够应用于实际工程中。随机矩阵的经验谱分布（empirical spectral distribution，ESD）函数当矩阵维数趋于无穷大、行数与列数之比保持不变时将满足一些特性。

1.1 圆环律与M-P 律

式中：c∈（0，1］，c 为常数。λ 分布在外径为1、内径为（1-c）2／L的圆环内。

1.2 平均谱半径

平均谱半径可用于高维矩阵统计特性的描述。随机矩阵的平均谱半径在系统有异常的信号源出现时，动态过程随着系统状态变化而变化，故常将其作为评估指标。其定义如式（2）所示：

2 复杂电网故障区域确定方法

为了确定故障发生的区域，通过建立增广矩阵将复杂电网中所有监测点中故障扰动数据作为状态数据矩阵，并将各个监测点故障扰动数据作为增广部分建立增广矩阵。根据随机矩阵理论分析增广矩阵与状态矩阵的相关性，相关性越高，表明该监测点更有可能与扰动区域接近，从而实现故障区域的确定。

2.1 数据处理

假设在复杂电网中，选择l 个节点的量测数据作为样本空间，监测每个节点k 个关键状态变量共形成N＝l×k 个状态变量。在采样时刻ti，所测量数据构成一个列向量，如式（3）所示：

将各个采样时刻的量测数据按照时间序列排列为一个状态数据矩阵，如式（4）所示：

采用实时分离窗法采集数据并进行分析以便进行实时计算，窗口宽度T，在采集i 时刻数据时，结合T-1 时刻数据共同形成矩阵：

由于监测所得数据并不满足单环定理所需数据要求，需要对原始矩阵x^进行数据处理，得到N×T维的非Hermitian 标准矩阵X¯：

求取X¯的奇异值等价矩阵：

对Z 进行标准化处理得Z：

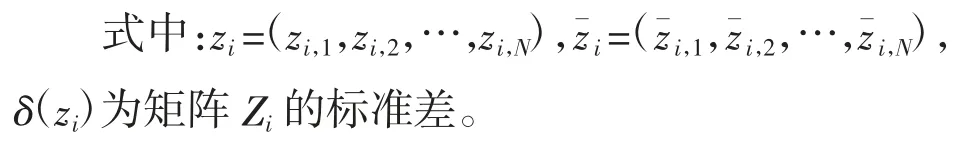
2.2 构建故障区域定位模型

假设系统存在p 个监测点，进行T 次采样得到状态矩阵Bc∈C（（p×pc）×T）与因素矩阵Bf∈C（（p×pf）×T）。其中状态变量pc个，影响因素pf个。

为降低重复数据对因素矩阵的影响，需要加入幅值大小为q 的随机噪声矩阵N 对影响因素矩阵进一步处理，如式（10）所示：

增广矩阵如式（11）所示：

利用Bc与N 建立参照状态增广矩阵，如式（12）所示：

在采样时间t1-t 内，定义平均谱半径差积分［18］：

式中：t1为采样开始时刻，t 为采样结束时刻。

QMSR（t）用来描述不同节点因素与该采样时间内电网状态之间的关联程度。采样周期内QMSR（t）值越大，说明在该节点系统状态受影响越大，节点所在区域更有可能成为故障发生区域。

2.3 故障区域定位流程

当电网中某一节点发生故障时，故障节点处数据关联程度高于其它节点，对应平均谱半径缩减程度变高。本文利用系统中模拟的故障线路，进一步确定故障区域，利用特征值的LMSR.A（t）对故障线路进行区段选择。基于RMT 的故障区域定位方法流程图如图1 所示。

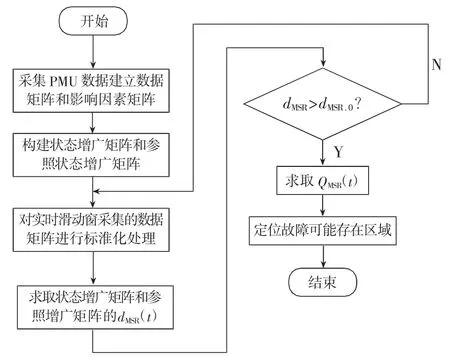
图1 电网故障区域确定流程图

3 算例分析

为验证复杂电网电压暂降故障区域定位方法的有效性，应用PSCAD 仿真软件，搭建IEEE-39节点系统模型，模拟电网电压暂降故障以获取数据，其结构如图2 所示。所取滑动时间窗大小40×110，为验证本文所提方法的有效性。

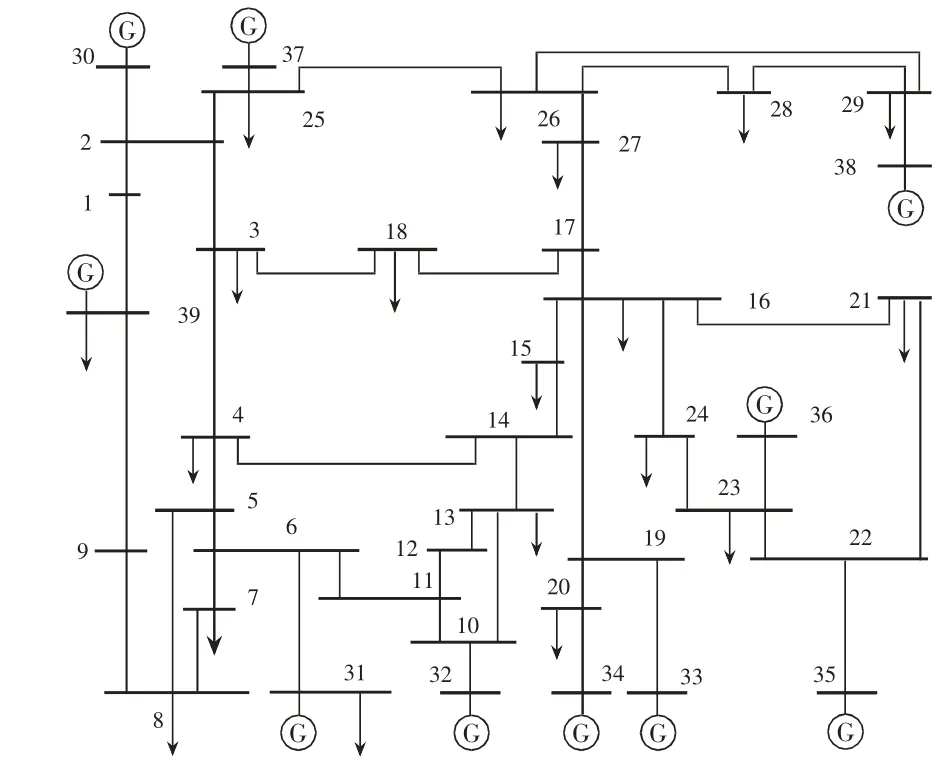
图2 IEEE-39 标准节点系统

场景一：设置节点11 和节点14 之间在t＝6s 时发生短路故障，t＝6.5s 时故障消除。

场景二：设置节点34 和节点35 之间在t＝6.2s时发生故障，在t＝6.7s 时故障消除。取所有节点电压幅值数据构造状态矩阵。

分别利用单环定理与M-P 律比较故障数据对系统的影响如图3、图4 所示。

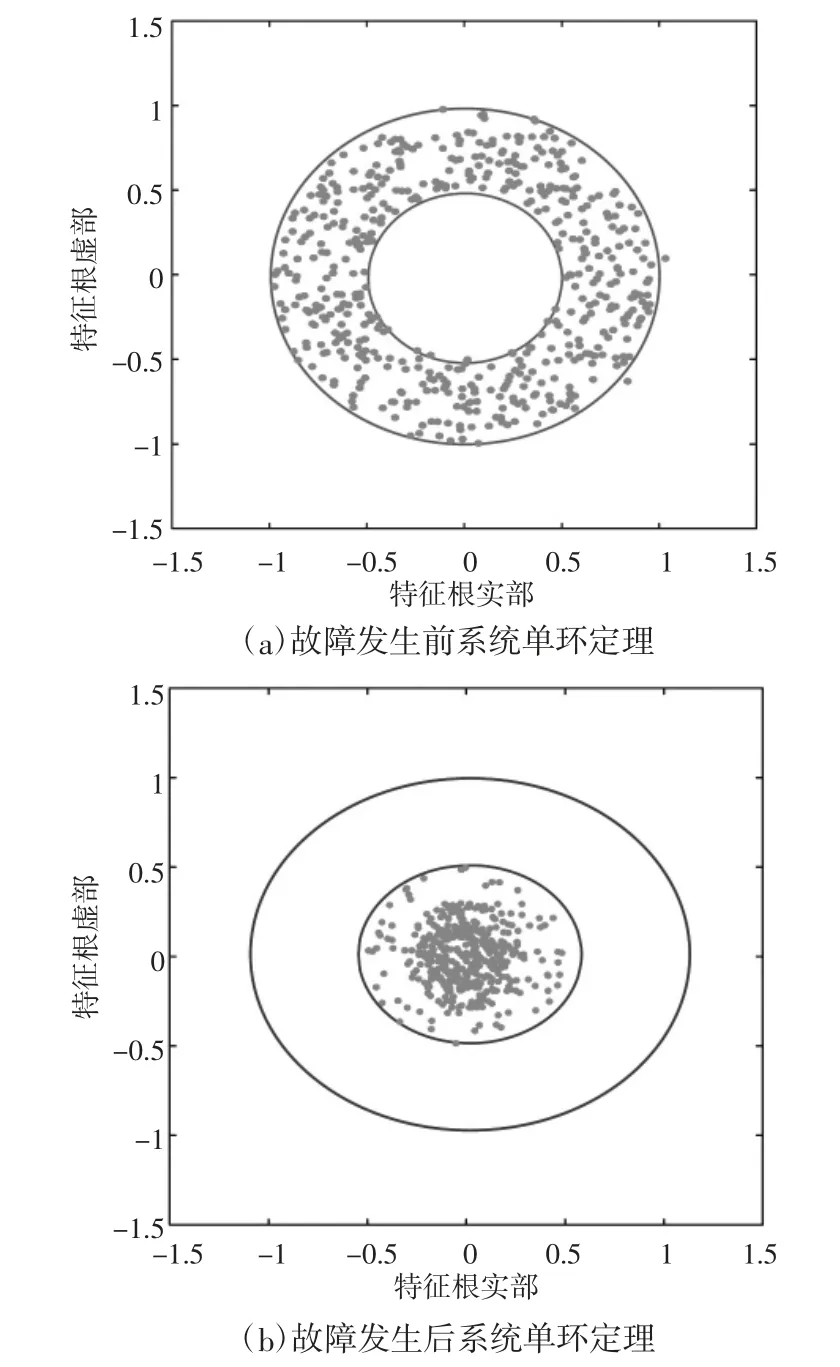
图3 故障前后单环定理效果图

由图3（a）可知，当系统处于故障发生前时，状态矩阵奇异值点分布在外环和内环之间，满足单环定理，个别外环点为异常数据导致。图3（b）可知，当系统在故障发生时刻时，奇异值点集中在内环之内，且分布较密集，不满足单环定理。

由图4（a）知，在故障发生前概率密度分布均匀，满足M-P 律，系统处于稳定状态。由图4（b）知，故障发生后，系统出现极端特征值，概率密度不均匀分布，不再满足M-P 律。

针对以上两个场景，根据所建立增广矩阵及参照增广矩阵求取矩阵QMSR（t）值。部分节点QMSR（t）值如图5 所示。

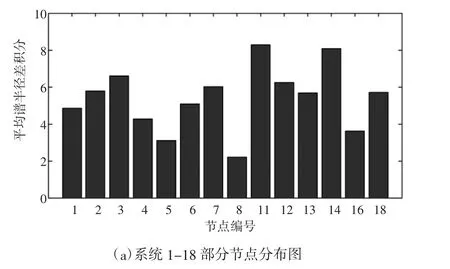
图5 系统部分节点分布图

由图5（a）可知，节点11 和节点14 的QMSR（t）值明显高于其他节点，说明故障发生对这两个节点的影响程度要高于其他的节点，这两个节点所在的区域更有可能为故障发生的区域。同理由图5（b）可知，节点34 和节点35 的QMSR（t）值高于其他节点，说明这些节点所在区域更有可能为故障发生的区域。

上述分析说明，在系统发生故障时，单环定理与M-P 律可以直观反应系统是否稳定。因此，本文所提方法能够较好地实现故障区域确定。

4 结论

本文从数据驱动的角度及电网的运行实际情况出发，提出了一种基于随机矩阵复杂电网故障区域的定位方法，通过2 个场景验证了方法的正确性，得到以下结论：

（1）复杂电网运行数据反映了系统的运行状态，传统分析方法难以分析处理大规模数据量，因此将随机矩阵理论引入复杂电网分析中，有效利用运行数据，可以明显提高诊断结果的准确性。

（2）应用单环定理及M-P 律判别电网的运行状态，分析状态增广数据之间的相关性，利用增广矩阵平均谱半径积分作为评价指标，能够准确定位故障发生的区域。该方法不仅能够有效降低数据矩阵的维数，还可以更快地分析数据。而且不受限于复杂电网的模型结构和运行机制，能够避免由于物理假设所带来的误差。