基于三维光谱指数的春小麦SPAD 高光谱估算

2023-10-17刘晓翠吾木提艾山江尼加提卡斯木

湖北农业科学 2023年9期

刘晓翠，吾木提·艾山江，尼加提·卡斯木

（伊犁师范大学生物与地理科学学院/资源与生态研究所，新疆伊宁 835000）

小麦（Triticum aestivumL.）作为中国重要的粮食作物，而超过95%的产量来源于叶片的光合作用［1］。叶绿素含量SPAD作为农作物光合作用中重要的参数之一，对叶绿素含量起到监测作用，有利于衡量农作物地上部分叶片光合能力［2，3］。快速、无损、准确地监测农作物长势对区域尺度水肥管理和估产具有重要的指导意义，也是发展智慧农业的需要。

随着遥感技术的迅速发展，尤其是高光谱遥感技术的不断提升，以其快速、无损和高效等优势在智慧和精准农业领域被广泛应用［4］。目前，利用高光谱遥感技术对作物主要参数（地上生物量［5］、叶片氮磷含量［6］、LAI［7］、叶片水分［8］等）进行估算，已经体现出明显优势。在农作物SPAD的遥感监测中，高光谱遥感发挥重要的作用，Al-Abbas 等［9］、Hinzman等［10］、Min 等［11］、Campbell 等［12］的研究表明了农作物冠层反射高光谱监测叶片SPAD的可行性。

已有的研究多采用原始波段反射率或一定数学变换构建的光谱指数进行建模与定量估算；郭燕等［13］通过全光谱原始数据进行建模预测小麦拔节期和成熟期的叶绿素含量，并对生育期变异进行制图。黄慧等［14］通过一阶、二阶微分以及多元散射校正等方法，对491~887 nm 波长的光谱反射率进行预处理，利用逐步回归法（Stepwise regression，SR）和偏最小二乘回归（Partial least-squares regression，PLSR）分别建立了估算小麦叶绿素含量的数学模型。同时，Bannari 等［15］通过室内高光谱数据计算PRI（531、550nm）、SRPI（430、680nm）、CARI（670、700nm）、PSSR（680、800nm）等敏感植被指数，并对冬小麦叶绿素含量进行估算。Wu 等［16］通过计算和整合高光谱植被指数TCARI（705、750nm）/OSAVI（705、750nm）和MCARI（705、750nm）/OSAVI（705、750nm），并与冬小麦叶绿素含量进行拟合，取得较好的研究成果。

目前，高光谱窄波段任意组合构建的3 波段光谱指数在一定程度上增强了研究对象的响应，在作物冠层氮指标和土壤有机质含量等参数估算中已有大量应用，并发现2 波段光谱指数的稳定性和估算能力弱于3 波段光谱指数，是目前寻求有效波段组合光谱指数研究的热点［17，18］。而在近些年研究成果中，基于任意窄波段组合构建3 波段光谱指数用于干旱区春小麦SPAD的研究还鲜有报道。鉴于此，本研究在400~1 300 nm 波段范围内，计算任意3 波段光谱指数，并分析对春小麦SPAD的响应；采用不同机器学习算法，进一步比较基于最优3 波段光谱指数的春小麦SPAD估算能力，筛选最优建模方法。为区域田间尺度快速、准确地评估作物长势动态与估产提供依据。

1 研究区概况与方法

1.1 研究区概况

研究区属于科学实验基地，位于新疆维吾尔自治区昌吉回族自治州阜康市上户沟乡滋泥泉子镇北部（88°22′—88°29′E，44°23′—44°22′N），实验基地周围均为播种小麦、玉米等农作物的大型农场［19］。研究区是典型的干旱耕作区，也是新疆主要的粮食基地。本研究的春小麦播种时间为2017 年4 月20日，每667 m2播种30 kg，行距17 cm。同时，参照当地农作物施肥灌溉方案，施磷酸二铵10 kg/667 m2、硫酸铵10 kg/667 m2、钾肥7 kg/667 m2［20］。播种区域均匀铺设滴灌设施（水量50~60 m3/667 m2）。气候类型属于典型的中温带大陆性干旱气候，其特点是四季分明，春秋气温变化较剧烈，年平均气温6.7 ℃，年平均降水量205 mm，光热条件充足［21］。图1、图2 为数据采样区域以及降水量和温度年内变化情况（2017 年）；采样区每个黄色正方形大小为1 m×1 m，共154 个采样小区。

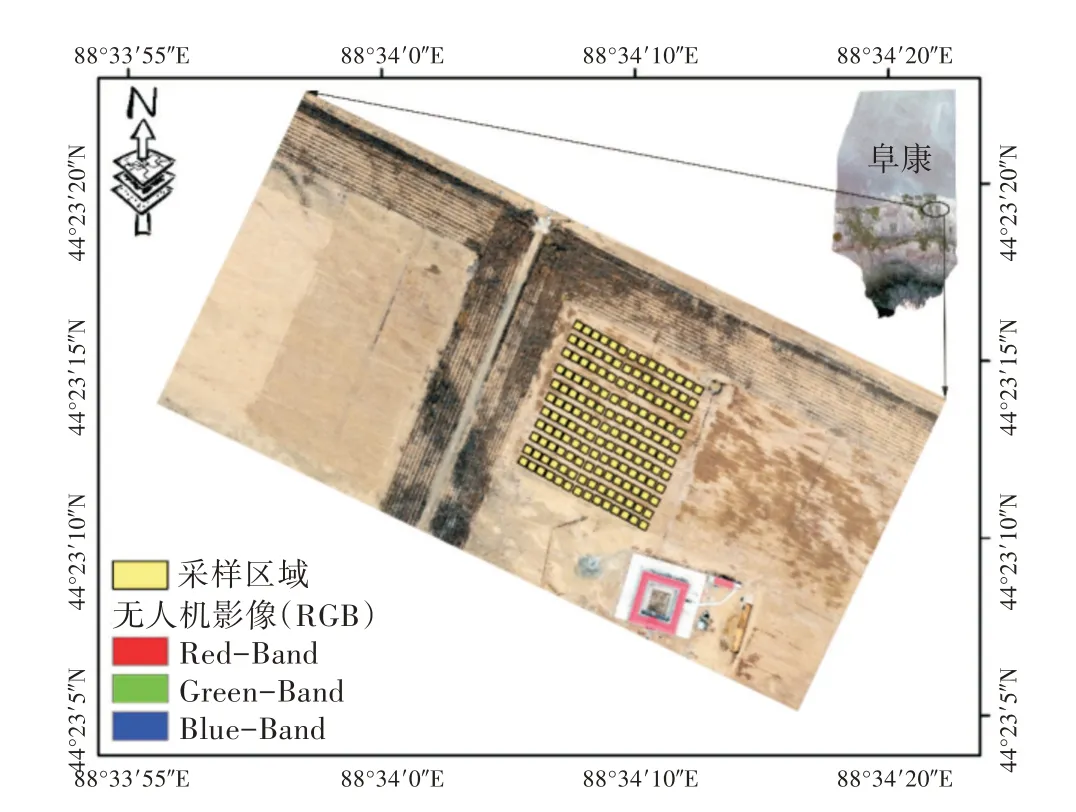
图1 数据采样区域

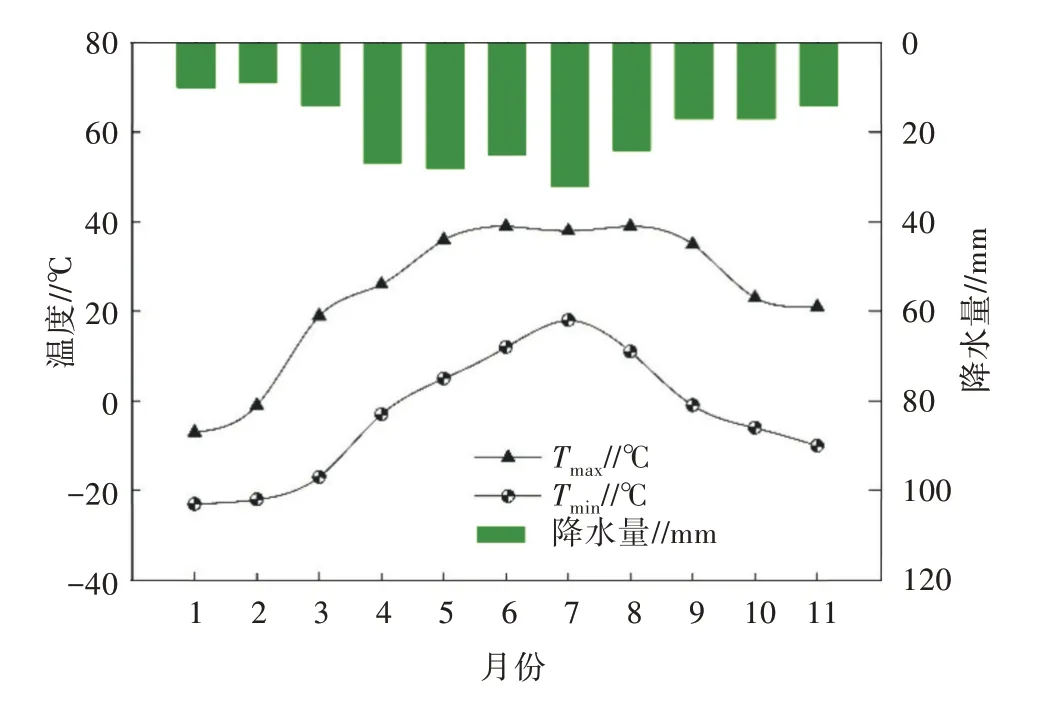
图2 2017 年降水量和温度变化情况

1.2 数据获取与处理

采用便携式叶绿素仪测量叶片对2 个波长范围的吸收率，评估植物叶片叶绿素相对含量，分析叶片叶绿素相对含量的变化趋势［22］。本研究于2017 年6月上旬在新疆维吾尔自治区昌吉回族自治州阜康科学实验基地进行样品采集，同时获取春小麦冠层高光谱数据。不同叶位叶片和叶位组合中，顶部叶片SPAD与反射光谱之间的定量关系较好［23］。本研究数据以春小麦顶一叶和顶二叶叶片的叶位组合为标准进行SPAD测定，重复测定10 次，计算平均值并将其作为该采样点的SPAD均值。

冠层高光谱数据采集是利用美国的ASD Field-Spec-3 光谱仪（波段范围为350~2 500 nm），在350~1 000 nm 和1 000~2 500 nm 波段采样间隔分别为1.4 nm 和2.0 nm，重采样后可达1 nm［24］。采集高光谱数据要具备以下3 个条件：①无云晴朗的天气；②时间保持在10：00—14：00；③每隔5 min 进行白板校正。每个样本重复采集10 次，取其平均值作为样本的冠层光谱数据。

1.3 三维光谱指数

光谱指数是通过目标物的光谱特征对波段反射率进行组合计算，不仅能充分考虑波段之间的相互关系，还可以有效地提高与目标物之间的度量关系［25］。在前人研究基础上，选取4 个三维光谱指数（TBI），数学表达式如表1 所示。

表1 三维光谱指数

本研究通过对TBI指数的3 个波长（Rλ1、Rλ2、Rλ3）重新组合，构建新的三维光谱指数。三维光谱指数计算在Java 平台上开发的软件（Three-band combination of optimized indices，V1.0.登记号：2018SR281300）中实现，并采用MATLAB（2014 版）软件制图。

1.4 估算模型的建立与验证

本研究采用3 种机器学习算法作为建模方法，构建估算模型并进行验证。人工神经网络（Artificial neural network，ANN）是指由大量的处理单元（神经元）互相连接而形成的复杂网络结构，是对人脑组织结构和运行机制的某种抽象、简化和模拟；以数学模型模拟神经元活动，是基于模仿大脑神经网络结构和功能而建立的一种信息处理系统［28］。

K 近邻（K-nearest neighbors，KNN）算法是一个理论上比较成熟的方法，也是最简单的机器学习算法之一。K 近邻算法的思路简单直观，如果一个样本附近的k个最近（即特征空间中最邻近）样本的大多数属于某一个类别，则该样本也属于这个类别［29］。支持向量机（Support vector machine，SVM）是一类按监督学习（Supervised learning）方式对数据进行二元分类的广义线性分类器（Generalized linear classifier），其决策边界是对学习样本求解的最大边距超平面（Maximum-margin hyperplane）［30］。主要是以最高的决定系数（Coefficient of determination，R2）和最低的均方根误差（Root mean square error，RMSE）来评价模型的稳定性和预测能力。计算公式如下：

式中，xi为实际变量为变量的平均值；i为变量数；N为变量总数；yi为预测变量为变量的平均值。

式中，γi为真实值；βi为预测值；n为变量总数。

相对分析误差（Relative percent deviation，RPD）指示模型的预测能力，计算公式如下：

式中，s为标准偏差；sx为标准误差。

根据模型的预测能力，当RPD>2.00 时，表明该模型具有较好的预测能力；当1.40≤RPD≤2.00 时，表明该模型具有一般预测能力；当RPD<1.40 时，表明该模型预测能力较差。

2 结果与分析

2.1 SPAD 统计及其高光谱的响应

将154 个样本按照SPAD从高到低进行排序，从高到低等间距选取变量作为建模集，剩余的作为验证集。表2 为春小麦抽穗期SPAD的统计分析结果。结果表明，建模集和验证集的SPAD均值分别为50.7和50.0，SPAD最小值分别为35.1 和28.8，SPAD最大值分别为60.4 和59.8，SPAD变异系数分别为9.3%和10.6%；全部采样区SPAD均值为50.4，SPAD变异系数为9.7%，介于建模集与验证集对应的SPAD和变异系数之间，呈中等变异性。

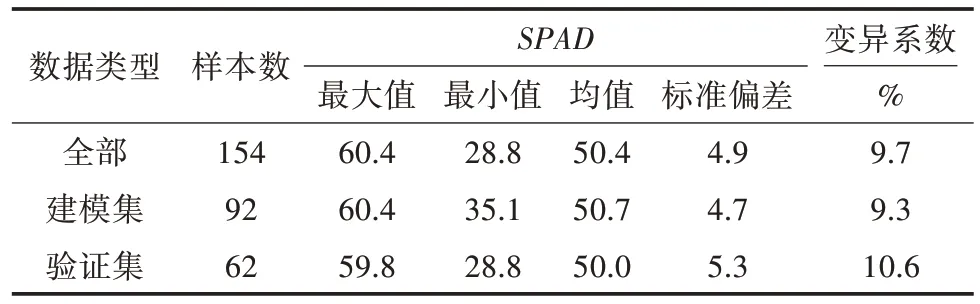
表2 研究区春小麦SPAD 统计特征

通过春小麦SPAD与波长400~1 300 nm 处反射率的相关性分析发现，在波长为400~522 nm 处光谱反射率呈极显著相关，通过了0.01 水平显著性检验（图3）；而在波长523~1 112 nm 处光谱反射率的相关性整体呈逐渐下降趋势，该波段处单波段反射率对SPAD的敏感性逐渐减弱。因此，本研究进一步考虑波段反射率之间的相互作用是否可以提高SPAD的敏感程度。

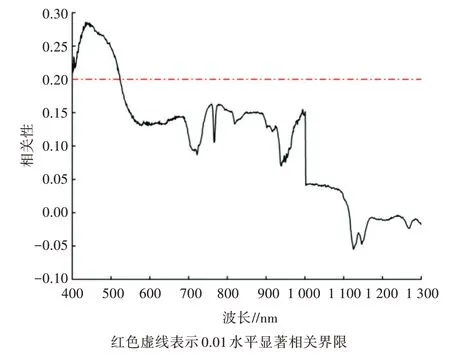
图3 春小麦SPAD 与高光谱反射率之间的相关性

2.2 SPAD 与TBI指数的关系

在400~1 300 nm 波段范围内，对三维光谱指数进行组合运算并与SPAD进行Pearson 相关性分析。借助MATLAB 环境分别绘制SPAD与三维光谱指数之间最敏感波段区域的三维相关性可视化热图，结果如图4 所示。

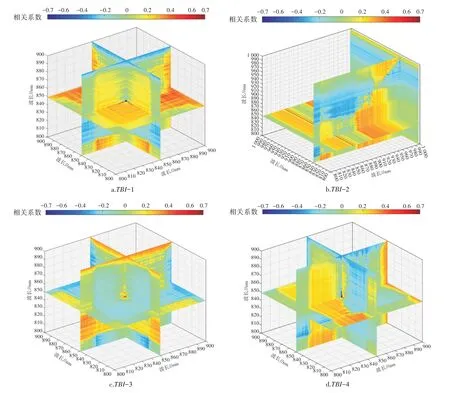
图4 SPAD 与三维光谱指数之间的Pearson 相关性

三维光谱指数对春小麦SPAD存在一定的敏感波段区域。近红外（700~1 000 nm）三波段组合计算能够使相关性更加突出，相关系数绝对值均达0.71（P＜0.01），通过MATLAB 软件内部插件筛选的最优波长分别为849、850、997 nm，本研究构建的三维光谱指数分别为TBI-1（849、850、850nm）、TBI-2（849、850、997nm）、TBI-3（850、849、850nm）、TBI-4（849、849、850nm），将三维光谱指数作为估算SPAD的主要光谱参数。与单波段的反射率相关性对比，敏感程度明显提高，相关系数从0.28提升到了0.71，表明三维光谱指数的运算对寻找更加敏感波段组合具有一定的贡献。

2.3 估算模型建立与验证

通过SPAD与单波段反射率和三维光谱指数之间的关联程度分析发现，不同类型的数据对其相关程度具有一定的差异。其中，任意波段组合构建的三维光谱指数与SPAD的关联程度明显提高。在数据建模中，通过显著性检验的单波段反射率和最优三维光谱指数参与建模过程；其中，通过显著性检验结果来确定敏感波段范围，敏感波段为400~522 nm，而对最优三维光谱指数的选取是依据最高相关性系数，本研究已选取的最优三维光谱指数分别为TBI-1（849、850、850nm）、TBI-2（849、850、997nm）、TBI-3（850、849、850nm）、TBI-4（849、849、850nm））。每一种数据类型选用3 种机器学习算法（KNN、SVR、ANN）作为建模方法，并根据模型评价指标进行对比分析，训练数据集与验证数据集的模型评价结果见表3。

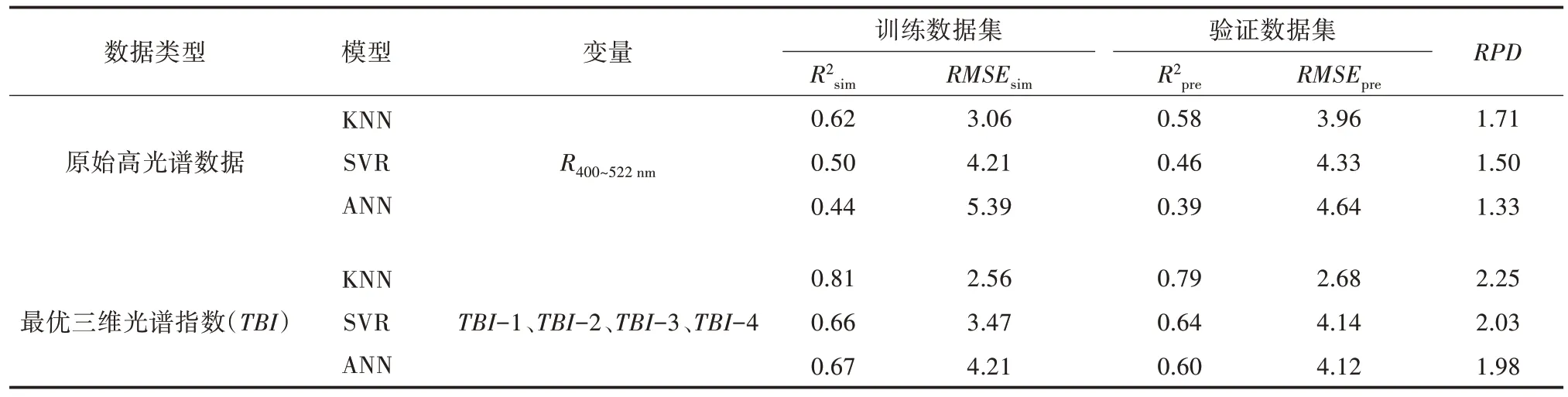
表3 春小麦叶片SPAD 建模与验证

从不同类型数据的建模中分析发现，3 种建模结果存在明显差异。其中，基于原始高光谱数据的建模效果及估算能力比较弱（R2分别为0.58、0.46、0.39），而基于最优三维光谱指数的建模效果及估算能力比较强（R2分别为0.79、0.64、0.60）；从数据模拟与估算能力分析发现，KNN 和SVR 算法在不同数据建模效果与估算能力中均处于较好的运算和模拟过程，利用最优三维光谱指数构建KNN 估算模型和SVR 估算模型，其相对分析误差RPD分别为2.25、2.03，利用原始高光谱数据、最优三维光谱指数构建ANN 估算模型，其相对分析误差RPD均低于2.00。

图5 是基于不同数据类型建模的验证值与估算值之间散点结果。结果表明，对春小麦SPAD的估算能力较好的数据类型为最优三维光谱指数，建模方法为K 近邻算法（KNN）；基于最优三维光谱指数（TBI-1、TBI-2、TBI-3、TBI-4）的KNN 算法拟合线更接近于标准1∶1 线，模型的估算效果分别为R2=0.79，RMSE=2.68，RPD=2.25。结合最高决定系数、最低的均方根误差和预测能力（RPD>2.00），选取KNN 模型作为本研究抽穗期春小麦SPAD的最优估算模型。

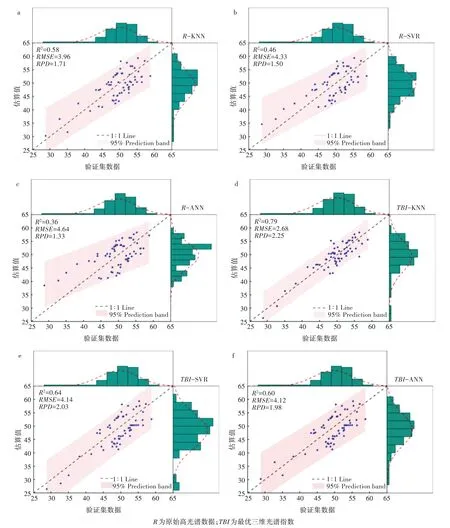
图5 春小麦SPAD 验证值与估算值之间的拟合效果

3 讨论

目前，小麦叶绿素相对含量SPAD遥感估算方法包括偏最小二乘法（Partial least squares regression，PLSR）、支持向量回归（SVM）、BP 神经网络算法等［31，32］，在作物参数估算领域表现突出，对精准农业和智慧农业的发展具有重要的意义［33］。本研究在田间尺度上以春小麦为目标，采集抽穗期冠层高光谱数据并计算任意波段组合的三维光谱指数，采用3 种机器学习算法分别构建基于最优三维光谱指数的春小麦SPAD估算模型，并对比其稳定性和估算能力，筛选最有效的估算模型。研究表明，在单波段反射率中，光谱反射率与SPAD显著相关的波段范围主要分布在可见光波段（400~500 nm），与前人研究成果一致［24，34］。虽然在400~522 nm 波段处光谱反射率全部通过0.01 水平显著性检验，但其与SPAD的相关性只有0.28。而对选取的4 种三维光谱指数来说，在400~1 300 nm 波段处进行任意窄波段组合，最优三维光谱指数与SPAD之间相关性显著提高，相关系数提升到0.71，且最优波段组合集中在光谱反射率的红边位置。张子鹏［18］等的研究发现，三维光谱指数可以在一维光谱参数（单波段反射率数据）和二维光谱参数的层面更深入地挖掘光谱信息，充分考虑窄波段之间的相互作用，有效提高地物参数的敏感程度。

本研究引入KNN、ANN 和SVR 3 种机器学习建模方法，通过3 种方法的分析发现，以单波段反射率构建的KNN 模型估算效果最好（R2=0.58，RMSE=3.96），而以最优三维光谱指数构建的KNN 模型估算效果最好（R2=0.79，RMSE=2.68）。在相同的自变量和因变量中，KNN 算法对数据的拟合效果比ANN和SVR 算法好。在诸多研究中，经常假设自变量和因变量呈线性关联而构建回归模型，在实际中线性关联条件的满足较难，吾木提·艾山江等［8］的研究表明最优窄波段植被指数与目标参数通常表现为非线性关系。本研究基于KNN 算法的建模精度优于ANN、SVR 算法，可能是由于选取的自变量和因变量数据更适合非线性拟合，表明3 种方法中KNN 算法在解决非线性拟合问题上表现突出。

本研究采用任意波段组合构建的三维光谱指数显著提高了对目标物的敏感程度，且利用KNN 建模方法提升了模型估算精度。同时，作物不同生育期叶片长势及大小具有一定的差异，这些与叶片光合作用有明显的影响；本研究的试验数据局限于春小麦抽穗期，因此三维光谱指数在各个生育期最优波段组合计算以及估算模型精度提升方面需要进一步优化，结合本研究模型在不同生长期进行验证与修正，提高模型的普适性与实用性。