汽车电动遮阳帘结构分析及系统阻力研究

唐荣华 王占 黄旸 王林 王琛

（广州汽车集团股份有限公司汽车工程研究院，广州 511434）

1 前言

天窗是车身系统中最大的机电一体化总成件之一。固定式全景天窗具有大尺寸、广视野、低成本、高可靠性以及可提供舒适的头部空间等优点，近年来应用广泛，与可开启式全景天窗相同，为解决车内遮光与隔热问题，需同时搭载遮阳帘[1-2]，随着车顶视野的不断增大，遮阳帘的开口尺寸也不断增大，并成为新的独立总成件，其布置形式、结构方案越来越丰富，技术难度也越来越高。

目前，国内对汽车电动天窗的机构运动、防夹与控制方面的研究较多[3-5]，蒋菲等[6]介绍了遮阳帘的硬挺整理工艺，提供了满足使用要求的帘布参数，李海帆等[7]提出了遮阳帘的同步驱动技术，新的结构使遮阳帘的张力更稳定。但是，汽车电动遮阳帘方面的独立研究很少，尤其缺乏对遮阳帘的系统研究。

本文对汽车电动遮阳帘进行结构分析，建立电动遮阳帘的基本模型，对遮阳帘展开与收卷过程中的运动部件进行详细受力分析，得到遮阳帘在运动过程中的受力状态与遮阳帘位置的关系，从而建立遮阳帘的系统阻力与其开口尺寸的数学表达式，识别影响各部件受力的潜在因素。

2 遮阳帘结构及其工作原理

2.1 遮阳帘的基本结构

遮阳帘的结构类型多样，但均采用口字型框架结构，主要由支撑框架、遮阳系统、驱动系统及控制系统组成。其中，支撑框架包括前梁、后梁、左/右导轨、软轴回管、软轴与滑块，遮阳系统包括卷轴、帘布、边条与拉杆，驱动系统与控制系统集成在电机总成上，如图1所示。

图1 汽车电动遮阳帘结构爆炸图

2.2 遮阳帘的工作原理

汽车电动遮阳帘总成典型结构如图2 所示，边条与帘布Y向连接，一端连接滑块，一端连接卷轴，整体嵌入两侧导轨的边条槽内，帘布受Y向张力达到绷紧状态，如图3 所示。在X方向，帘布一端连接拉杆，一端连接卷轴，在卷轴卷收力作用下，帘布X向受力达到绷紧状态，如图4 所示。帘布周圈均受张力而均匀展开在支撑框架内，关闭状态时，拉杆处于m位置，对应软轴区间为a-b-c-d-e-m，打开状态时，拉杆处于n位置，对应软轴区间为g-d-e-n。

图2 遮阳帘总成结构原理

图3 遮阳帘Y向张紧示意

图4 遮阳帘X向张紧示意

电机在Q处通过齿轮与软轴啮合，在控制系统的指令下运转，带动软轴在滑槽内线性移动，从而通过控制电机的转动来实现遮阳帘的开闭运动。根据遮阳帘的运行过程分析，汽车电动遮阳帘基本结构件及其约束类型如表1所示。

表1 汽车电动遮阳帘基本结件及其约束类型

3 遮阳帘运行部件受力分析

本文研究的电动遮阳帘结构见图2，相关参数如下：Y向开口为830 mm，X向行程为1 200 mm，帘布面密度为280 g/m2，最大出布角为30°，软轴转角曲率半径约为90 mm，转角圆弧处包角为90°，软轴长为1 880 mm，直径为4.7 mm，线密度为80 g/m，边条支撑角度α=arctan0.5，边条与帘布厚度相等且均为0.6 mm，摩擦因数统一取为0.2，卷轴杆外径为20 mm，卷轴弹簧实测刚度为0.06 N·mm/(°)，帘布初拉力为(15±5) N。基于以上参数与电动遮阳帘三维数据，并结合表1，对遮阳帘5个基本运动子件进行受力分析。

3.1 软轴受力分析

软轴是遮阳帘运动过程中的关键传动部件，受到多个复合力的作用。以单侧软轴为例，遮阳帘在运行过程中软轴受力可分解成滑槽摩擦力fm、转角A处的软轴挤压带来的阻力fA与转角B处的软轴自由端变形带来的阻力fB。

软轴在导轨、导槽及回管内的运动方式等同于线缆在管道内的运行模型[8]，如图5 所示，其中V为软轴的运动方向，得到软轴直线段平衡方程为：

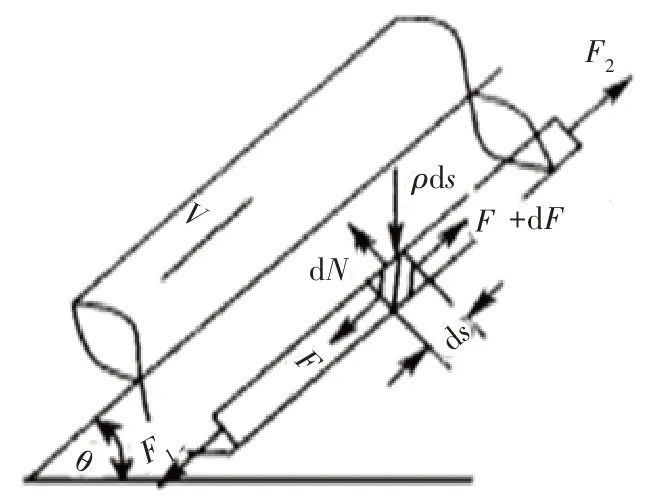
图5 软轴在直线段的运动受力简图

式中，θ为导轨与水平面夹角；μ1为软轴与导轨的滑动摩擦因数；ρ为软轴的线密度；F为单位长度软轴所受初始张力；dN为单位长度软轴所受支撑力；ds为单位软轴的长度；dF为单位长度软轴的驱动力。

合并式（1）与式（2）求积可得：

式中，F2为软轴驱动端受力；F1为软轴从动端受力；S为软轴驱动端到从动端的长度。

由式（3）可知，软轴在滑槽内的移动与运动方向无关，与软轴长度线性相关。根据样件尺寸，求得软轴在滑槽内的摩擦力为：

经计算，fm=0.3 N。

软轴在转角A处的运动受力如图6 所示，忽略圆弧处软轴的质量，得到软轴全包角处的平衡方程为：

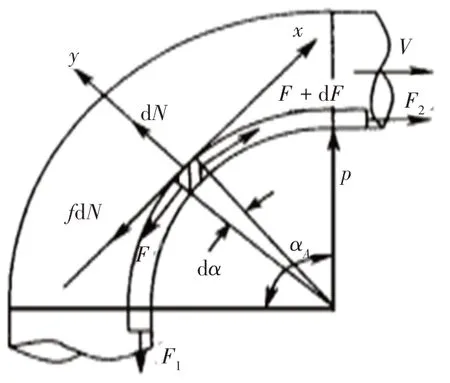
图6 软轴在转角A处的运动受力简图

式中，αA为圆弧包角；μ2为软轴与软轴槽的滑动摩擦因数。

由式（5）和式（6）可得：

由式（7）可知，软轴在转角A处所受阻力与软轴转弯半径无关，与所经过弯道的包角和软轴摩擦因数相关。根据样件结构及其尺寸参数，Q处软轴的啮合力FQ等于遮阳帘系统阻力，可得软轴在转角A处的拉拽力fAL与推送阻力fAT分别为：

经计算，fAL=0.27FQ，fAT=0.37FQ。

软轴在转角B处的运动受力简图如图7 所示，等效一端固定的圆柱悬臂梁末端受力产生变形的过程[4]。圆弧包角αB为变量，没圆弧中心半径为q，软轴末端受管壁正压力为FB，软轴的圆柱形截面惯性矩I=πd4/64，软轴弹性模量EZ=16.3 GPa，软轴末端导向头长度为10 mm，末端悬臂长度为L=q·sinαB+10，软轴末端变形量为ω=-q(1-cosαB)，且不计圆弧处软轴的质量，得到软轴末端的挠度方程为：

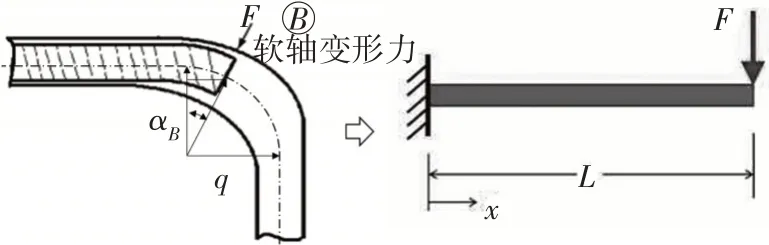
图7 软轴在转角B处的运动受力简图

由式（11）可知，软轴末端在圆弧内的受力的影响因素较多且关系较为复杂，与软轴运动方向无关，受转弯半径和弯道包角影响较大。根据样件结构及其尺寸参数，求得软轴转角B处的阻力fB为：

3.2 滑块受力分析

滑块是遮阳帘运动过程中的关键连接部件，分别装配连接遮阳帘拉杆和遮阳帘边条，并通过一体注塑与软轴连接，在导轨内滑动，如图8所示。

图8 滑块在导轨上的装配简图

为避免滑块在运行过程中产生振动异响，且考虑到生产装配工艺，滑块与导轨为局部过盈配合，通常其直线运行阻力fh=(5±2)N。

3.3 帘布受力分析

帘布是遮阳帘总成中的主要部件，帘布展开遮阳时分别受到Y向张紧力TY与X向张紧力TX。以下出布为例，没卷轴杆外径d0=20 mm，单层帘布厚度t=1.2 mm，帘布X向受力如图9 所示，帘布收卷圈数n、卷轴展开转角φn与帘布展开行程Sn的几何表达式分别为：

图9 帘布在X向的受力示意

式中，d1为预卷2圈后外径；dn为卷绕n圈时外径。

卷轴帘布出布角αn=β0+βn，其中β0与卷轴布置相关，角度表达式为：

式中，β0为卷轴布置角，取值为19°；βn为收卷n圈后的帘布切角；L0为帘布出布点到卷轴中心的距离，取值为95 mm。

帘布运行时，切点O动态变化，以O点为原点建立直角坐标系，忽略帘布变形，得到帘布向运动方受力平衡方程为：

式中，T1为帘布出布张力；T2为帘布展开时的X向张力；θ1为坐标系下出布张力夹角；θ2为坐标系下X向张力夹角；fON为帘布受到导布横梁的摩擦力；μ3为帘布与导布横梁的摩擦因数；T为帘布受到导布横梁的正压力。

由式（18）～式（21）可得：

忽略出布角变化的影响，经计算，TX=1.11T1。

由于帘布介于两侧边条之间，取导轨在X向的剖面，帘布的Y向张紧等效悬链曲线模型[9]，受力模型如图10 所示。其中，M、N分别为边条两侧固定点，Oy为帘布的最低点，P为圆弧MN上的任意一点，λ为Y向帘布单位长度的质量，l为帘布弧OyP的长度。以Oy为原点建立直角坐标系，静止状态的平衡方程为：

图10 悬链线静止状态时的受力情况

式中，TP为P处帘布张力；θP为P处帘布张力的水平切角；TO为最低点Oy处水平张力。

由于遮阳帘两侧导轨水平布置，帘布最低点Oy距左侧边条固定点M的竖直高度yM与帘布最低点Oy距右侧边条固定点N的竖直高度yN相等且为该截面上帘布的最大下垂量，由式（23）～式（25）可得：

式中，L为帘布圆弧MN的长度；Dy为边条固定点M与N的水平距离；θN为N处帘布张力的水平切角；TN为N处帘布张力。

由式（28）可知，帘布Y向张力受导轨跨距、帘布面密度以及帘布下垂量影响。为保证帘布运行平稳且运行过程中帘布整体处于张紧状态，不能忽略帘布弹性变形，一般通过调整帘布宽幅尺寸Δl来调整Y向的预紧力。根据样件结构及其尺寸参数，等效下垂量yN=18 mm，帘布横向弹性系数为0.05 N/mm，得到帘布Y向张力TY为：

3.4 边条受力分析

遮阳帘边条在导轨处主要受到垂直运动方向的正压力与平行运动方向的摩擦力，如图11 所示。其中，NB为作用在边条上的正压力，TB为帘布对边条的拉力，TB=TY，θB为帘布跨点处角度，αB为边条支撑角度，FZ为导轨对边条的正压力，NZ为导轨对帘布的正压力。

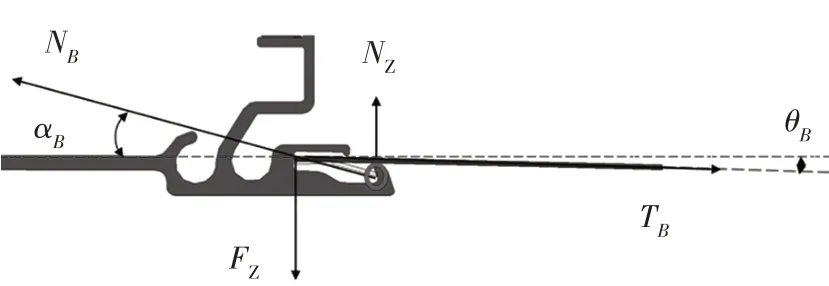
图11 遮阳帘边条在导轨处的受力简图

得到遮阳帘边条Y方向平衡方程为：

由式（30）～式（32）可得单侧边条在导轨上的阻力fB：

式中，μB为边条与导轨的摩擦因数；dx为帘布运行距离；S为帘布运行行程。

边条在后梁上的受力主要作用在导向块位置，如图12 所示。导向块位置与帘布出布点在Y向基本处于同一位置，由于X向受力主要作用在边条上，摩擦因数一致时，帘布与边条在后梁处的摩擦阻力fHL等效于帘布在导布横梁处受到的摩擦力fON与边条在导轨上的阻力fB之和，由式（19）～式（21）可得：

图12 遮阳帘边条在后梁导向块处的受力简图

根据样件结构及其尺寸参数，忽略出布角变化的影响，得到边条在两侧导轨上的总阻力fBZ=2fB。经计算，fBZ=65.56S2×10-7，fHL=0.074n。

3.5 卷轴扭矩模型

遮阳帘回退时，帘布主要通过卷轴扭转力回收，其结构如图13所示，其关键部件为回收弹簧，为螺旋扭转弹簧，受力如图14所示。

图13 遮阳帘卷轴结构爆炸图

图14 卷轴内扭转弹簧受力

扭转弹簧按受弯矩的曲梁计算[10-11]，其扭转角φ以及弹簧的扭转刚度k的数学表达式分别为：

式中，d为簧丝直径；M为扭转弹簧弯矩；D为扭转弹簧中径；n1为扭转弹簧有效圈数；E为簧丝弹性模量。

由式（13）、式（14）得：

式中，F0为卷轴初始拉力。

由式（37）可知，卷轴扭矩受弹簧丝直径、弹簧中径、有效卷绕圈数及扭转角度影响。对于受动负荷弹簧，应进行疲劳强度校核[12]，以满足遮阳帘1.0×104～1.5×104次的操作耐久要求。根据样件结构与尺寸及卷轴弹簧扭转刚度，求得卷轴转动时对横梁的摩擦阻力为：

4 遮阳帘系统阻力分析

根据本文提出的遮阳帘结构，以车前方向为正方向，啮合点Q处为系统阻力基准点，遮阳帘打开状态为运行起始点，以软轴末端为运动行程参照，设R为与运行方向无关的各分阻力总和，得到遮阳帘打开与关闭时的系统阻力表达式分别为：

式中，foff为遮阳帘关闭时的系统阻力；fopen为遮阳帘打开时的系统阻力。

根据式（40）和式（41），分别对a、b、B、c、g位置进行采点计算，实测a与b的距离为600 mm，B与b、B与c的距离相等，为100 mm，c与g的距离为400 mm，同时对样件相应位置进行阻力实测，得到遮阳帘系统运行阻力曲线，如图15 所示，实测系统阻力与计算结果在变化趋势上有很好的一致性。

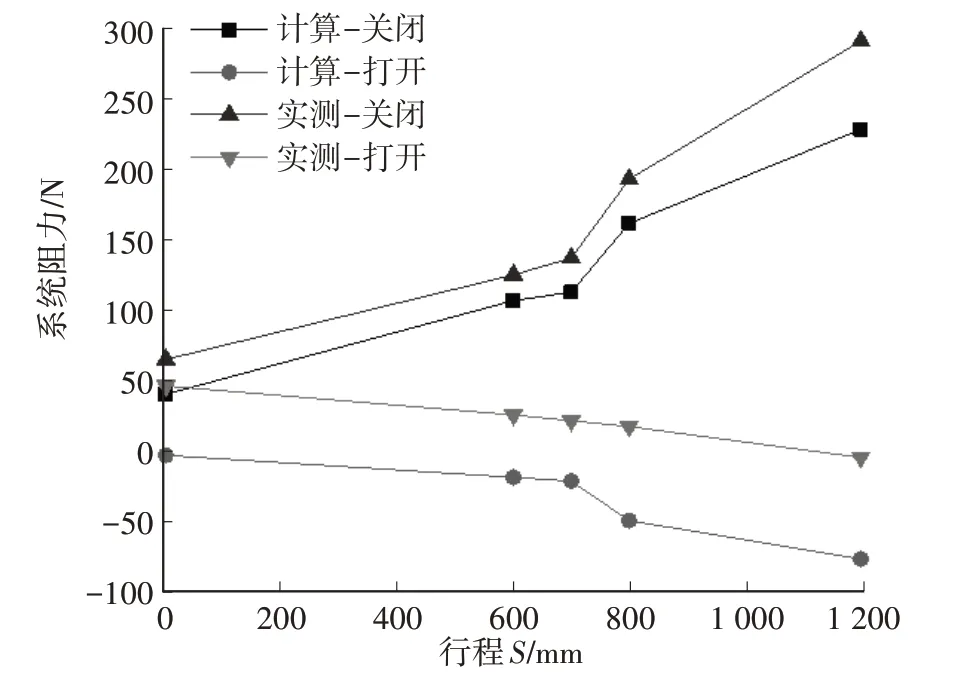
图15 遮阳帘系统运行阻力曲线

5 结束语

本文对汽车电动遮阳帘的运行过程及其受力状态进行了系统分析，并建立了遮阳帘的系统阻力与其开口行程的数学表达式，结果表明：遮阳帘系统阻力受力状态复杂，影响因素繁多，主要为遮阳帘开口尺寸、软轴曲率半径、转角数量与圆弧包角、帘布面密度、伸缩率及帘布下垂量、摩擦因数、卷轴初拉力/末拉力等，其中卷轴内弹簧卷收力影响最大，各运动部件之间的匹配关系及帘布属性影响最敏感，即遮阳帘系统阻力主要由卷收方式及卷收力决定，遮阳帘系统阻力的稳定性主要由运动部件几何关系决定。