定向在流形路径上连续延拓的存在唯一性
2023-10-17郭烨徐宏飞
郭烨,徐宏飞
定向在流形路径上连续延拓的存在唯一性
郭烨,徐宏飞
(湖北师范大学文理学院,理工学院,湖北 黄石 435109)
流形是微分几何中的主要研究对象,流形可根据是否可定向分为可定向流形与不可定向流形,可定向流形与不可定向流形有着诸多不同的性质.定向在流形路径上连续延拓的存在唯一性为可定向这一性质定义的理论基础,利用实变函数、拓扑学相关知识,给出了定向在流形路径上连续延拓存在唯一性的一个证明方法.
定向;流形路径;连续延拓
1 引言及预备知识
流形是微分几何中的主要研究对象,流形可根据是否可定向分为可定向流形与不可定向流形,可定向流形与不可定向流形有着诸多不同的性质[1-6].定向在流形路径上连续延拓的存在唯一性为可定向这一性质定义的理论基础.
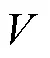
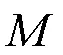
本文证明了定向在流形路径上连续延拓的存在性与唯一性.
2 主要结果及证明
定向在流形路径上连续延拓的存在唯一性为流形可定向这一性质定义的理论基础,对于微分几何理论的发展具有重要意义.本文给出了定向在流形路径上连续延拓存在唯一性的一个证明方法,该方法的过程清晰严密,可为相关研究提供参考.
[1] 高山珍.二维可定向流形的几个定理(英文)[J].贵州师范大学学报(自然科学版),2003(1):40-43.
[2] 雷逢春,翟延慧,张军,等.紧连通可定向带边3-流形的一个表示[J].吉林大学自然科学学报,1995(3):6-8.
[3] 徐森林,周坚.不可定向流形上Laplace算子的特征值[J].数学研究与评论,1991(3):377-382.
[4] 丁帆.不可定向四维流形的一些例子(英文)[J].数学进展,2002(1):37-40.
[5] 詹华税.可定向的具非负曲率完备非紧黎曼流形[J].数学进展,2001(1):70-74.
[6] 于书敏.微分流形上的Stokes公式[J].通化师范学院学报,2006(4):121-122.
[7] 丘维声.高等代数学[M].北京:清华大学出版社,2019.
[8] 徐森林,胡自胜,金亚东,等.点集拓扑学[M].北京:高等教育出版社,2007.
[9] 陈维桓.微分几何初步[M].北京:高等教育出版社,2001.
[10] 白正国.黎曼几何初步[M].北京:高等教育出版社,2004.
Existence and uniqueness of continuous continuation of orientation on the manifold path
GUO Ye,XU Hongfei
(School of Science and Technology,College of Arts and Science of Hubei Normal Unversity,Huangshi 435109,China)
Themanifold is an important research object in differential geometry,manifolds can be divided into orientable manifolds and non-orientable manifolds according to whether they are orientable or not,orientable manifolds and non-orientable manifolds have many different properties.Existence and uniqueness of continuous continuation of orientation on the manifold path are the theoretical basis of the definition of orientable manifold.A method to prove the existence and uniqueness of continuous continuation of orientation on the manifold path is given by using the knowledge of real variable function and topology.
orientation;manifold path;continuous continuation
1007-9831(2023)09-0022-04
O189.3+1
A
10.3969/j.issn.1007-9831.2023.09.006
2022-11-14
湖北师范大学文理学院2022年校级科研项目(KY202203)
郭烨(1992-),男,湖北黄冈人,讲师,硕士,从事基础数学研究.E-mail:3045654895@qq.com
