有色噪声干扰下Hammerstein非线性模型辨识

宋 伟, 韩佳虎, 李 峰*, 曹晴峰

(1.江苏理工学院 电气信息工程学院, 江苏 常州 213001; 2.扬州大学 电气与能源动力工程学院, 江苏 扬州 225127)

0 引言

Hammerstein非线性模型同时结合了动态线性特征和无记忆非线性特征,可以描述一大类实际非线性过程,被广泛应用于实际工业过程的辨识建模与控制.围绕Hammerstein模型的参数辨识问题,领域内的专家研究出了一些重要的方法,主要分为同步辨识和分步辨识两大类.同步辨识包括过参数化法[1,2],子空间法[3,4],直接辨识法[5,6]等,这类辨识方法通过构造系统的混合参数模型,直接辨识原模型混合参数,然后进行各子系统参数分离.分步辨识包括迭代法[7,8],频域法[9],多信号源法[10-13]等,这类辨识方法通过重构中间变量,实现模型子系统之间的参数分离辨识.

在Hammerstein非线性模型的参数辨识中,最小二乘方法因其概念简单、易于实现而成为非线性模型辨识的主流算法[14].考虑SISO(Single Input Single Output)Hammerstein模型的辨识问题,文献[15]在递推最小二乘算法中引入变遗忘因子,解决了由于参数映射带来的收敛速度下降问题.基于关键项分离技术,Ding等[16]将Hammerstein受控自回归系统分解为若干个变量较少的子系统,利用递阶最小二乘算法辨识子系统参数.文献[17]针对Hammerstein非线性输出误差系统,利用辅助模型的输出代替未知变量,提出了一种基于辅助模型的最小二乘辨识算法.考虑一类输入非线性误差系统,文献[18]将关键项分离技术结合辅助模型方法,研究了基于关键项分离的辅助模型最小二乘辨识方法.上述方法中研究了Hammerstein模型的外部噪声为白噪声的参数辨识问题,得到一致的参数估计.

系统的外部噪声有两种形式,即白噪声和有色噪声.与白噪声相比,有色噪声具有一般性和代表性[19].当外部噪声为有色噪声时,上述各类最小二乘辨识方法无法得到系统参数的一致估计[14],其原因是递推辨识算法没有对噪声模型的参数进行估计,因此对有色噪声干扰下Hammerstein模型辨识的关键在于能够有效估计有色噪声模型.根据有色噪声的产生机理,有色噪声可由白噪声生成[20],可以利用自回归模型[21],滑动平均模型[22,23],或者自回归滑动平均模型[24]进行拟合.针对带有色噪声的状态空间模型的辨识问题,文献[25]基于递阶辨识原理,推导了状态观测器的递阶随机梯度算法,对参数向量和状态进行联合估计.考虑一类Hammerstein FIR-MA-like系统,文献[26]基于数据滤波技术,探究了一种基于数据滤波随机梯度辨识方法.针对Hammerstein非线性受控自回归滑动平均系统,文献[24]研究了一种基于牛顿迭代的最大似然估计方法.上述文献研究了不同类型有色噪声干扰的Hammerstein模型辨识方法,并取得相应的辨识结果.值得强调的是上述辨识方法在辨识过程中出现Hammerstein模型参数乘积项,在设置非线性子系统或者线性子系统的首项参数为1的条件下分离出线性和非线性子系统的参数值.因此这类方法降低了模型辨识精度,且具有一定的局限性.

针对上述问题,本文考虑一类滑动平均噪声的干扰,研究了有色噪声干扰下Hammerstein模型参数分离辨识.研究中设计了由二进制信号和随机信号构成的组合信号,并利用二进制信号不激发静态非线性子系统的特性实现Hammerstein模型各串联子系统分离辨识,解决了Hammerstein模型中间变量信息不可测量问题.首先,基于二进制信号的输入/输出数据,采用AV-RELS(Auxiliary Variables Recursive Extended Least Squares)方法辨识线性子系统和滑动平均噪声模型的参数,实现参数一致估计.其次,基于随机输入信号及其输出,通过本文提出的FF-ESG(Forgetting Factor based Extended Stochastic Gradient)方法,可以有效的改善非线性子系统的辨识效果.

1 滑动平均噪声干扰下Hammerstein非线性模型

考虑如图1所示的一类滑动平均噪声干扰下Hammerstein非线性模型.

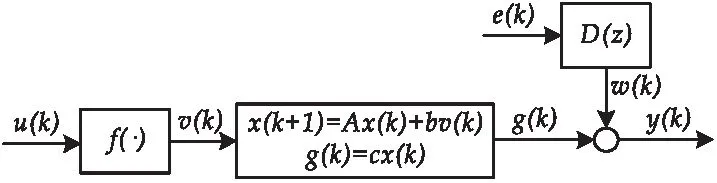
图1 滑动平均噪声干扰下Hammerstein非线性模型结构图

根据图1所示,滑动平均噪声干扰下Hammerstein模型的数学描述如下所示:

v(k)=f(u(k))

(1)

x(k+1)=Ax(k)+bv(k)

(2)

g(k)=cx(k)

(3)

w(k)=D(z)e(k)

(4)

y(k)=g(k)+w(k)

(5)

式(1)～(5)中:f(·)表示静态非线性子系统,u(k)和v(k)分别是非线性子系统的输入和输出,g(k)是线性子系统的输出,y(k)是Hammerstein模型的输出.e(k)和w(k)分别是有色噪声模型的输入和输出,D(z)=1+d1z-1+…+dndz-nd是单位后移算子的多项式,dj是噪声参数,nd是噪声模型的阶次.x(k)是状态空间变量的矩阵x(k)=[x1(k),x2(k),…,xn(k)]T,A是状态空间的参数矩阵,b和c是状态空间的参数向量,b=[b1,b2,…,bn]T,c=[1,0,…,0],

采用多项式模型拟合Hammerstein模型的非线性子系统,非线性子系统的表达式如下:

v(k)=f(u(k))=
p1h1(u(k))+p2h2(u(k))+…+
prhr(u(k))=hT(u(k))P

(6)

式(6)中:P=[p1,p2,…,pr]T∈Rr×1是多项式模型的参数向量,hT(u(k))是关于输入u(k)的基函数向量,h(u(k))=[h1(u(k)),h2(u(k)),…,hr(u(k))]T.

对于滑动平均噪声干扰下的Hammerstein非线性模型辨识问题,我们的目标是对于任意给定的阈值ε,求解满足下列约束条件的参数:

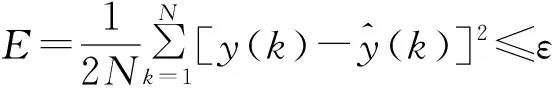
(7)

式(7)中:“∧”表示估计,N表示模型的数据长度.

2 滑动平均噪声干扰下的Hammerstein模型参数辨识

为了解决中间变量v(k)不可测的问题,设计特殊的组合式信号实现Hammerstein模型参数的分离辨识.所设计的组合式信号包括幅值为0或λ的二进制信号和随机信号.前期的研究结果表明[27,28]:当二进制信号作为输入信号u(k)时,非线性子系统的输出信号v(k)也是二进制信号,即v(k)与u(k)是同频率不同幅值的二进制信号,如图2(a)所示.使用常数增益β对u(k)的幅值进行补偿,中间变量v(k)就可以用输入信号u(k)代替,如图2(b)所示.因此,可以实现静态非线性子系统和动态线性子系统的参数分离辨识.

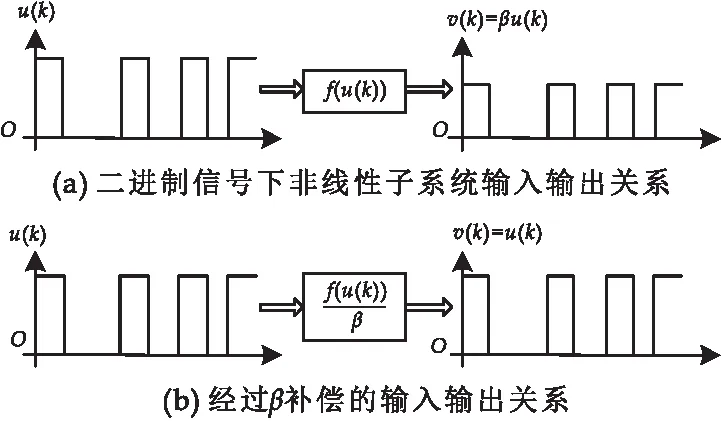
图2 二进制信号在非线性系统下的特性

2.1 动态线性子系统和滑动平均噪声模型的参数辨识

当Hammerstein模型的输入为二进制信号u1(k)时,根据公式(2)可以得到:

xi(k+1)=xi+1(k)+biv(k)(i=1,2,…,n-1)

(8)

xn(k+1)=-anx(k)-an-1x(k)-…-
a1x(k)+bnv(k)

(9)

利用单位后移算子z-1的性质,分别在公式(8)的两边同时乘以z-1,公式(9)的两边同时乘以z-n,然后可以得到:

(10)

公式(10)可以简化为:

(11)

根据公式(3)～(5)和公式(11),Hammerstein系统的输出表达式为:

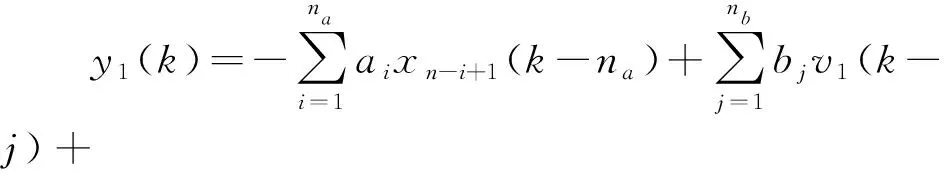
(12)

利用二进制信号的特殊性质,公式(12)中的v1(k)可以用b0u1(k)代替:

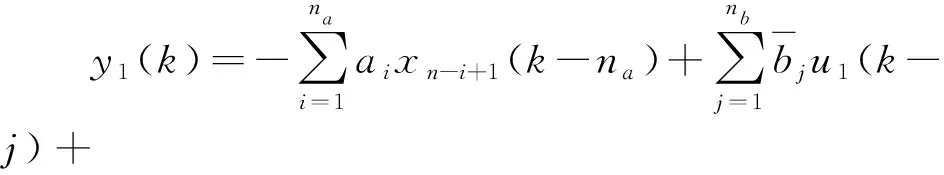
(13)

将公式(13)写成线性回归形式:

(14)

式(14)中:θ1=[a1,…,ana,b1,…,bnb,d1,…,dnd]T,φ1(k)=[-xna(k-na),…,-x1(k-na),u1(k-1),…,u1(k-nb),e(k-1),…,e(k-nd)]T.

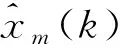
定义准则函数如下:

(15)

可以推导基于辅助变量的递推增广最小二乘算法,辨识出线性子系统和滑动平均噪声模型的参数.

(16)

(17)

(18)

(19)

(20)

2.2 静态非线性子系统的参数辨识

为了辨识静态非线性子系统的参数,采用随机信号u2(k)作为Hammerstein模型的输入,根据公式(6)和公式(12),可以得到输入输出表达式:

(21)

转化为线性回归形式:

(22)

定义准则函数如下:

(23)

针对定义的准则函数,将增广随机梯度算法用于参数辨识.为了提高辨识精度,在增广随机梯度算法的基础上引入遗忘因子[15,29],推导了如下遗忘因子增广随机梯度算法:

(24)

(25)

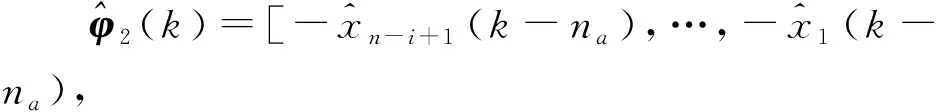
(26)

(27)

(28)

3 仿真研究

为了证明提出的算法的有效性,采用本文提出的算法对滑动平均噪声干扰下的Hammerstein非线性模型进行参数辨识.考虑如下Hammerstein非线性模型

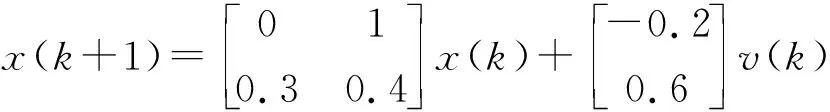
(29)

定义噪信比为

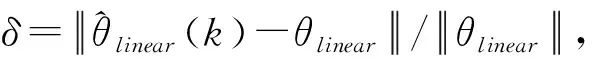
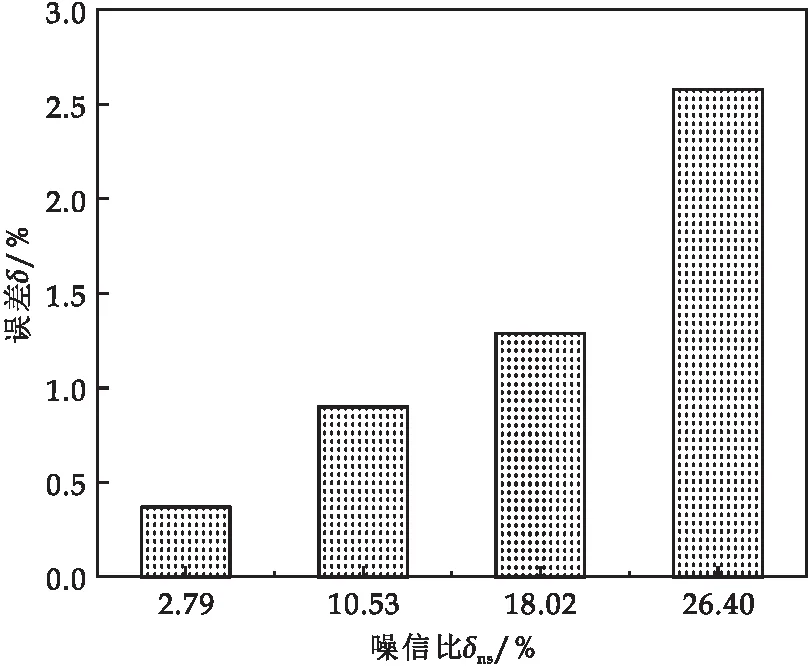
图3 不同噪信比下的参数辨识误差

噪信比是指模型中噪声与信号的比例,噪信比δns越大,表示噪声对模型的影响越大,反之则越小.为了说明提出的方法能够有效处理有色噪声的干扰,图3选取了四类不同噪信比,且逐渐增加.从图3中容易看出,随着噪信比δns的增加,线性子系统参数辨识的误差百分比虽然有所增加,但总体相对稳定,且不超过30%.因此,本文提出的方法能够有效辨识有色噪声干扰下的Hammerstein模型.

为了说明提出的方法和加权增广随机梯度方法[30]对有色噪声模型参数的辨识效果,图4和图5选取了两类不同噪信比,且逐渐增加.

图4 δns=6.61%时噪声参数辨识结果

图5 δns=15.67%时噪声模型参数辨识结果

从图4和图5中可看出,与加权增广随机梯度方法相比,本文提出方法的噪声模型参数的估计值更接近真实值.随着噪信比δns的增加,本文提出方法的效果更加明显.

第二阶段：根据随机信号及其对应的输出信号,采用2.2节推导的遗忘因子增广随机梯度算法对非线性子系统进行辨识.仿真中,遗忘因子λ=0.877.为了更好的证明所提出算法的优越性,将推导的算法与RELS算法[31],GI算法(Gradient-based Iterative)[32]和AM-RELS算法(Auxiliary model based Recursive Extended Least Squares algorithm)[33]进行对比,四种算法对非线性子系统的拟合结果如图6和表1所示.

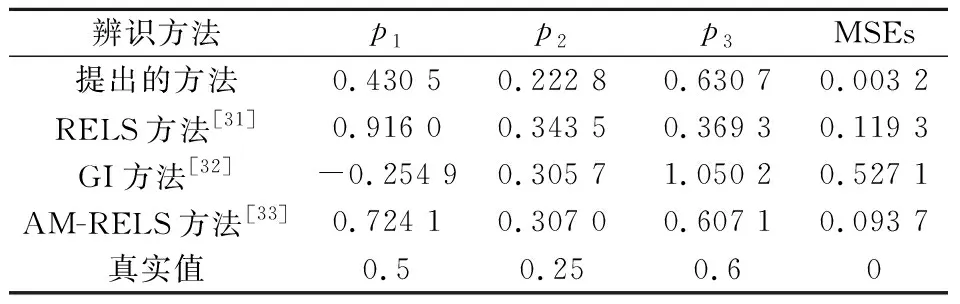
表1 非线性子系统的辨识误差

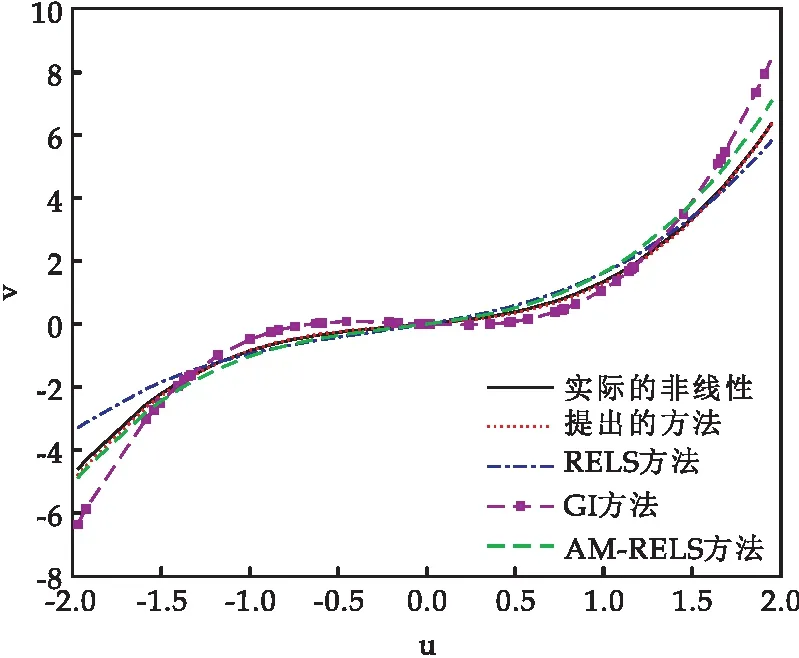
图6 四种辨识算法对非线性拟合结果比较

从图6和表1可看出,相较于RELS方法,GI方法以及AM-RELS方法,本文推导的方法在对Hammerstein模型的非线性子系统辨识时,具有更高的辨识精度.本文提出的遗忘因子增广随机梯度方法,由于在算法中引入遗忘因子,增加记忆长度,使辨识精度提高.迭代梯度方法遍历整个数据集时,每次更新并不是向着最优的方向进行,往往出现局部最优,导致无法得到整体最优解.递推增广最小二乘非线性辨识方法虽然收敛速度较快,但在有色噪声干扰下效果不理想.辅助模型递推增广最小二乘方法在辨识过程中因辅助模型阶次的选择不同,导致辨识结果存在一定的偏差.

增广随机梯度(ESG)方法计算量小,但收敛速度慢.为了提高增广随机梯度方法的收敛速度和辨识精度,在增广随机梯度方法中引入遗忘因子.遗忘因子是误差准则函数中的加权因子,不同的遗忘因子代表对旧数据不同的遗忘速度.随着遗忘因子增大,模型的收敛速度加快,但误差变大;随着遗忘因子减小,模型的误差变小,但收敛速度变慢.因此,选择合适的遗忘因子可以平衡收敛速度和误差.从图7可以看出,当遗忘因子λ=0.877时,非线性子系统拟合效果最好.

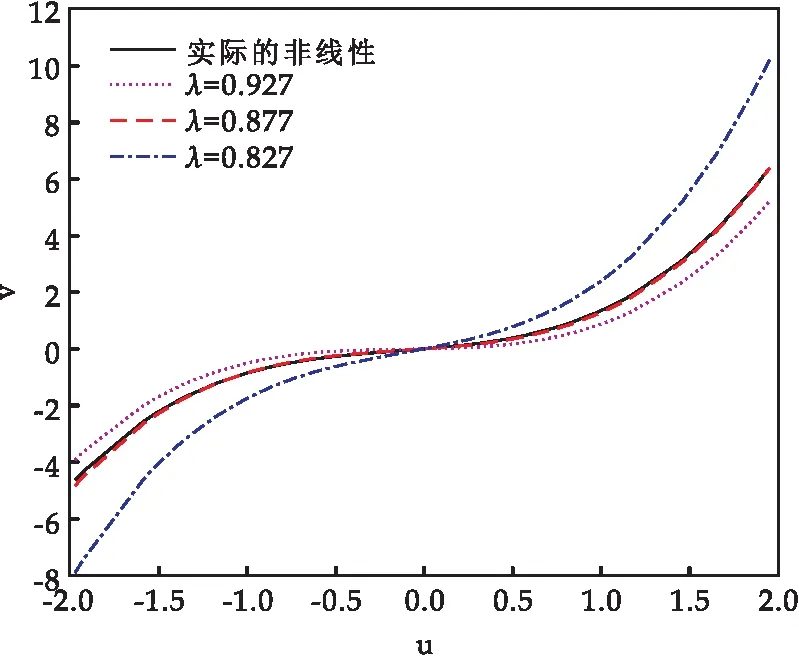
图7 不同遗忘因子的非线性拟合结果比较

4 结论

本文针对有色噪声干扰的Hammerstein模型的参数辨识问题,提出了一种智能分离辨识方法.通过设计特殊的组合式信号,分别对静态非线性子系统和动态线性子系统进行参数辨识.首先,采用二进制信号作为Hammerstein模型的输入,分析其不激发非线性子系统的性质,通过AV-RELS方法辨识出线性子系统和有色噪声模型的参数.其次,将系统的不可测状态变量用估计值代替,利用随机信号的输入输出数据,采用FF-ESG方法得到非线性子系统的参数.仿真结果验证了所推导的智能分离算法Hammerstein模型的参数具有较高的辨识精度.