具p-Laplacian算子的半正分数阶脉冲微分方程三点边值问题解的存在性与唯一性

盛世昌, 张婷婷, 胡卫敏,2*

(1.伊犁师范大学数学与统计学院, 新疆 伊宁835000;2.伊犁师范大学应用数学研究所, 新疆 伊宁 835000)

整数阶的微分方程有关于p-Laplacian算子和脉冲边值条件的文献[1-4],分数阶微分方程中关于带p-Laplacian算子的方程研究已取得不少成果[5-10],关于带脉冲边值条件的问题研究文献也逐渐增加[11-20],而分数阶微分方程中两个条件同时具备的相关研究文献较少. 在一些复杂力学过程中,其经验公式一般表现为幂律函数的形式,这种力学过程具有记忆、遗传和路径依赖等性质. 整数阶导数在解决复杂力学问题时,需要构造非线性方程,引进复杂的假设条件,这就造成了这些模型在求解时的困难.分数阶微分算子相比之下,能简洁且准确地刻画具有记忆性和空间全域相关性的物理力学过程.本文参考整数阶微分方程的相关研究文献,讨论了一个具p-Laplacian算子的半正分数阶微分方程三点脉冲边值问题解的存在性,利用Banach和Schauder不动点定理,获得了解的存在性的充分条件．

文献[8]讨论了具p-Laplacian算子非线性分数阶微分方程的边值问题

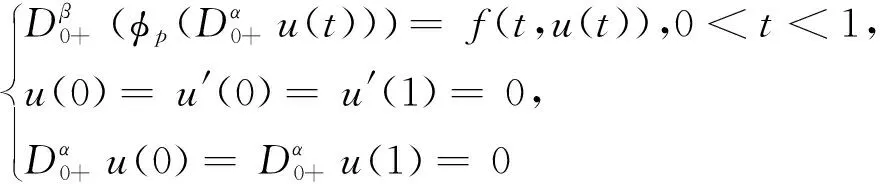
(1)

文献[10]分析了具p-Laplacian算子的分数阶微分方程三点边值问题

(2)

文献[11]研究了非线性分数阶脉冲微分方程三点边值问题

(3)

的不动点,用Banach不动点定理证明了方程解的存在性和唯一性,其中,1<α≤2,f∈C(J×,),为Caputo分数阶导数．

本文讨论下列具p-Laplacian算子的半正分数阶微分方程三点脉冲边值问题

(4)

1 预备知识

设J0=[0,t1],J1=(t1,t2],…,Jm-1=(tm-1,tm],Jm=(tm,1],空间PC(J,)存在,定义范数(J,)={u：J→|u∈C1(Jk),k=0,1,…,m},且存在,定义范数(J,),PC1(J,)是Banach空间．

定义1[11]函数f：[0,+∞)→,α阶Riemann-Liouville分数阶积分是指

其中,右边是在[0,+∞)逐点定义的．

定义2[11]函数f：[0,+∞)→,α>0,α阶Caputo型分数阶微分是指

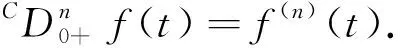
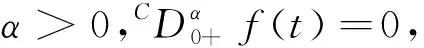
f(t)=c0+c1t+c2t2+…+cn-1tn-1,ci∈,i=0,1,2,…,n-1,n=[α]+1．

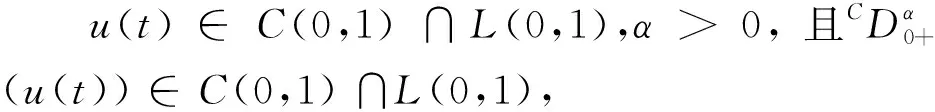
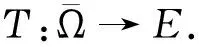
引理4[14](Arzela-Ascoli定理)K⊂PC(J,)是相对紧的,当且仅当函数u(t)∈K在J上一致有界,在Jk上等度连续．

引理5[14](Schauder不动点定理)设X是Banach空间,D⊂X是有界凸闭的(D不一定存在内点),T：D→D是全连续的,则T在D中存在不动点,即存在x*∈D,使得Tx*=x*．

引理6设y∈C(0,1),且ξ∈(tl,tl+1),l为非负整数,0≤l≤m.u∈PC1(J)是边值问题

(5)

的解等价于u是如下积分方程的解,

(6)

其中,

证明设u是方程(5)的解,对方程(5)两边同时求α阶积分,由引理1可得,当t∈J0时,存在常数c1,c2∈,使

(7)

当t∈J1时,存在常数d0,d1∈,使

则

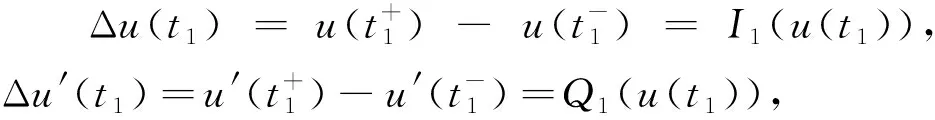
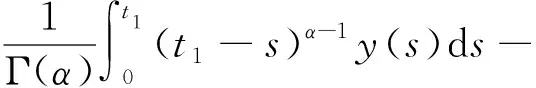
c1-c2t1+I1(u(t1)),

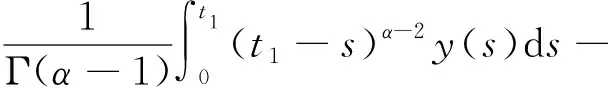
c2+Q1(u(t1)).

故

(t-t1)Q1(u(t1))-c1-c2t,t∈J1.

重复以上步骤,类似可得

(8)

由边值条件u(0)+u′(0)=0,得c1+c2=0,由(7)可得

由u′(ξ)+u(1)=0和c1+c2=0,可得

将c1、c2代入 (7)、(8),设M=c2,可证得方程(6)．

2 解的存在性

设ξ∈(tl,tl+1),l为非负整数,0≤l≤m.定义T：PC1(J,)→PC1(J,),

由引理6可知,T的不动点是方程(4)的解,下面用Banach压缩映像原理证明．

定理1(H1)设存在常数L1>0,使得

|φq(f(t,x))-φq(f(t,y))|≤L1|x-y|,

对∀t∈J,x,y∈．

(H2)设存在常数L2,L3>0,使得

|Ik(x)-Ik(y)|≤L2|x-y|,|Qk(x)-Qk(y)|≤L3|x-y|,

对∀t∈J,x,y∈,k=1,2,…,m.

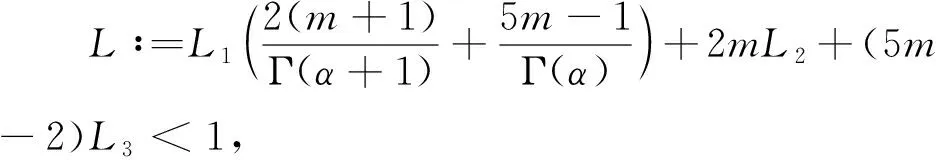
证明对∀x,y∈PC1(J,),有

|(Tx)(t)-(Ty)(t)|≤

(5m-2)L3|x-y|≤

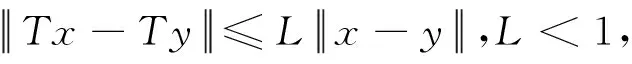
定理2(H3)设φq(f(t,u(t)))：[0,1]×→是连续的,且存在常数N1>0,使得|φq(f(t,u(t)))|≤N1,对∀t∈J,u∈．

(H4)设Ik,Qk：→是连续的,且存在常数N2,N3>0,使得|Ik(u)|≤N2,|Qk(u)|≤N3,对∀t∈J,u∈,k=1,2,…,m．

当上述条件成立时,方程(4)有一个解．

证明下面用Schauder不动点定理证明T存在不动点．

第一步,证明T是连续的．

设函数列{un}∈PC1(J),且un→u,

|(Tun)(t)-(Tu)(t)|≤

φq(f(s,u(s)))|ds,

第二步,证明T将有界集映成有界集,即T一致有界．

2mN2+(5m-2)N3,

因此有

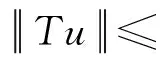
第三步,证明T是等度连续的．

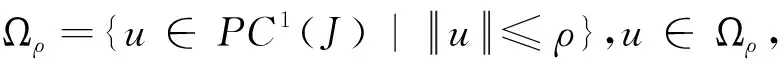
因此,设t1,t2∈Jk,t1

M|t2-t1|,

所以T(Ωρ)在任意的Jk上是等度连续的,可以得出结论T：PC1(J,)→PC1(J,)是全连续算子．

第四步,证Ω={u∈PC1(J) |u=λTu,0<λ<1}有界．

设u∈Ω,则有u=λTu,0<λ<1,因此对∀t∈J,有

由(H3)、(H4)可得,对∀t∈J,

2mN2+(5m-2)N3,

因此对∀t∈J,有

(5m-2)N3,

即Ω是有界的,由上面的证明,再根据Schauder不动点定理可得,T有一个不动点,也就是方程(4)的解．

3 举例

方程

(9)

其中,

这里显然φq(f(t,u)),I,Q都连续,且

1)|φq(f(t,u))|≤1,对∀t∈J,u∈;

2)|I|≤3,|Q|≤5,对∀u∈．

满足条件(H3),(H4),由定理2可得,方程(9)有一个解．

分数阶微分方程作为整数阶微分方程的推广,具有比整数阶微分方程更长远的发展价值.在众多学者的努力下,此方面研究取得了很大的进步.但由于脉冲边值条件的处理难度较大,以及各种新型算子的加入,未来的研究还是具有一定的挑战性.研究具有p-Laplacian算子的分数阶奇异脉冲微分方程边值问题也存在改进的空间,如果将p-Laplacian算子改为p(t)-Laplacian算子,是一个不错的研究方向,接下来笔者也将对这个方向展开研究．