基于改进粒子群算法的配电网故障恢复研究
2023-10-16王以琳谢华北闫杨舒崔世庭朱瑞金
王以琳, 谢华北, 闫杨舒, 高 遥, 崔世庭, 朱瑞金
(1.西藏农牧学院 水利土木工程学院, 西藏 林芝 860000; 2.西藏农牧学院 电气工程学院, 西藏 林芝 860000)
0 引言
近些年来,极端天气造成配电网停电事故屡次出现.配电系统位于电力系统的末端,直接向用户提供电能,当突发故障引起大停电时,会造成巨大的损失,严重影响人们的日常生活[1-3].提高配电系统的故障后恢复能力显得尤为重要.含分布式电源(distributed generation,DG)的配电网故障恢复可以使故障后的失电负荷得到快速恢复,是提高配电系统韧性的重要途径[4,5].
目前,相关学者对含DG的配电网故障恢复策略做了大量研究.文献[6]提出了一种考虑DG间歇性的孤岛划分方法,对用户侧负荷进行时序性建模,保证了重要负荷优先恢复.文献[7]提出了一种针对复杂配电网的故障恢复策略,首先利用孤岛划分对重要负荷进行供电,其次依据启发式规则对剩余失电负荷进行恢复.文献[8]提出了将孤岛划分与重构技术相互配合的故障恢复策略,投入相应的联络开关,使得大部分的失电负荷得到了恢复,取得了较好的恢复效果.文献[9]建立了一种考虑DG和储能出力的故障恢复模型,考虑了时间尺度和故障检修策略,对模型进行了凸松弛,降低了求解的复杂程度.
目前研究配电网故障恢复重构的算法主要是启发式算法、数学规划法和智能优化算法.智能优化算法原理简单、收敛性好被广泛运用于配电网故障恢复重构中.文献[10]采用一种基于粒子群优化算法(PSO)的主动配网故障恢复方法,与蚁群算法进行对比,可以有效的处理主动配网故障恢复重构,具有稳定性好、效率高的优点.文献[11]采用一种改进的“破环”粒子群优化算法对配电网进行故障恢复重构,引入动态惯性权重和学习因子,与传统粒子群算法对比能更好的实现故障自愈.文献[12]将故障网络分为可恢复停电区和不可恢复停电区,在可恢复停电区域采用整数编码的量子粒子群优化算(ICQPSO)进行恢复重构,提高了配电网的供电可靠性.文献[13]采用改进的灰狼算法对剩余网络进行恢复重构,引入莱维分布的随机搜索方法,可达到快速恢复供电和降低网损的效果.
上述研究主要存在以下问题:(1)在配电网故障恢复期间,大部分研究没有考虑用户侧负荷的灵活特性,没有考虑到不同类型负荷的时变需求,导致风-光-储系统的出力不能充分利用,造成资源的浪费;(2)当前配电网的故障恢复,部分研究只利用单一技术进行故障恢复,没有将孤岛划分与重构技术进行相互配合,不能保证全网供电量达到最大;(3)配电网故障重构算法在迭代后期搜索能力逐渐减少,种群多样性降低,且容易陷入局部最优.
针对上述研究存在的问题,文章提出一种计及风-光-储联合出力和负荷灵活性的配电网故障恢复策略,该策略考虑了用户侧的负荷需求,充分利用可控负荷的灵活特性,使得重要负荷优先恢复,并将孤岛划分与重构技术的相结合,使得更多的失电负荷得到恢复.然后,采用改进粒子群算法(improved particle swarm optimization,IPSO)对剩余部分进行重构,达到最优供电恢复效果.最后以IEEE33节点配电系统仿真验证模型的有效性.
1 风储、光储和负荷特性模型
1.1 分布式电源和储能联合出力模型
文章假设储能装置在单位时间内的充放电功率相同,将储能充放电模型用充电状态(state-of-charge,SOC)表示,储能装置的数学模型为:
(1)
考虑储能装置的过充、过剩以及电池寿命问题.需要对储能的剩余容量和充放电功率进行限制,其约束条件为:
(2)
(3)
(4)
(5)
为了提升DG的稳定性,使孤岛系统更加稳定运行.将DG和储能进行联合出力,其出力模型如下:
Pp(t)=Pb(t)+Pc(t)
(6)
式(6)中:Pp(t)为光储或风储联合出力;Pb(t)为光伏系统或者风力系统的出力,文献[14]描述了其具体出力过程;Pc(t)为储能装置的充、放电功率.
1.2 负荷特性模型
1.2.1 负荷时变性模型
在不同的时间段内,不同类型的负荷有不同的时变需求.文章中考虑三种负荷类型,即政府医疗负荷、居民负荷和商业负荷.对三类典型日负荷进行曲线积分,最终得到不同种类负荷在各个时间段的用电需求为:
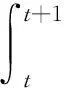
(7)
式(7)中:Li(t)为节点i在t时段内的负荷用电需求;fi(x)为负荷曲线函数.
1.2.2 负荷重要程度
依据负荷停电造成的人身伤害和经济损失可以分为一级、二级和三级负荷[15].在断电时,一级负荷要优先保障100%恢复.其次,要根据不同的时刻确定优先恢复的重要负荷,其优先恢复系数为:
ωi,t=λi,tDi,t
(8)
式(8)中:ωi,t为负荷优先恢复系数;λi,t为负荷权重;Di,t为负荷时间尺度重要系数.一级负荷设置为10,其他负荷按照负荷需求设置权重.
1.2.3 可控负荷
可控负荷作为配电网中重要的用户侧管理资源,不仅可以提高负荷的恢复率,而且对可控负荷进行削减,还能保证重要负荷优先恢复.可控负荷的节点示意图如图1所示.

图1 可控负荷节点示意图
文中假设二级负荷和三级负荷可作为可控负荷,在对可控负荷削减时,优先削减重要程度较低的三级负荷,在对孤岛边界可控负荷供电时优先恢复重要程度较高的二级负荷,文中对签订协议的可控负荷进行削减,其表达式如下:
(9)
2 孤岛划分
2.1 孤岛划分模型
2.1.1 目标函数
孤岛划分模型一般是以恢复重要失电负荷的总电量为目标,孤岛划分的目标函数如下式:
(10)
式(10)中:f为目标函数;T为故障持续时间;yi,t为恢复供电的状态,当yi,t为1时,在t时段内恢复供电,当yi,t为0时,则在t时段内未恢复供电.
2.1.2 约束条件
(1)功率约束
(11)
式(11)中:n为DG数量;D为孤岛内负荷节点数量;Pb,t为在t时段内光储或风储的联合出力值.
(2)节点电压约束
Umin≤Ui,t≤Umax
(12)
式(12)中:Umax和Umin分别为节点i的上下限电压幅值.
(3)功率平衡约束
(13)
(14)
式(13)~(14)中:Pi,t和Qi,t分别为节点i在t时段内有功和无功功率;n为节点总数;Ui,t和Uj,t分别为在t时段内,支路首端和末端的电压幅值;Gij、Bij和δij,t分别为在t时段内,支路ij的电导、电纳和电压相角;ΔQi,t为节点i的无功补偿量.
(4)容量约束
Sij,t≤Sij,max
(15)
式(15)中:Sij,t为支路ij在t时段内的功率;Sij,max为支路ij的允许的最大功率.
(5)配电网辐射状约束
g∈G
(16)
式(16)中:g为供电恢复后的网络拓扑结构;G为辐射状网络拓扑结构.
2.2 孤岛划分策略
利用光储和风储作为故障时刻的出力电源,对不同的故障时刻进行动态孤岛划分,具体步骤如下:
(1)首先,确定每个时段内光储或风储的最大出力值,并根据故障线路确定相应的失电负荷.
(2)其次,利用广度优先搜所算法进行初步划分,以光储和风储所在的节点为根节点开始,至故障支路所在节点结束.在划分时保证重要负荷优先恢复.
(3)若孤岛外存在未恢复的重要负荷,孤岛内存在可控负荷,对孤岛内的可控负荷按照重要等级进行排序,优先削减重要程度低的可控负荷.其供电原则按照孤岛内的剩余电量和可控负荷的削减量联合出力对重要负荷恢复供电.
(4)若孤岛内没有可控负荷,而孤岛外边界存在未恢复的可控负荷,将孤岛外边界的可控负荷按照重要等级排序,将光储和风储的剩余容量按一定比例给可控负荷进行部分电力供应.
3 故障恢复重构
考虑孤岛与重构相配合,需调整联络开关状态集.然后对剩余网络进行重新编号,利用主网对剩余网络进行重构恢复供电,并采用改进的粒子群算法(IPSO)对模型进行求解.
3.1 故障恢复重构模型
配电网的故障恢复重构首要目标是减少重要负荷的失电量,其次是网损和开关操作次数.文章以最小网损和最少开关操作次数为目标建立目标函数:
(17)
式(17)中:T为故障持续时间;E为支路总数;Ω为节点总数;Iij为支路ij电流的平方;R为支路ij的电阻;x0为重构前开关的初始状态,x为重构的开关状态,闭合为1,断开为0;a1,a2为目标函数中的权重,按照实际需求,取a1为0.7,a2为0.3.
3.2 传统粒子群算法
粒子群算法(PSO)是一种基于群体协作的智能优化算法,其基本思想是通过种群的协作和信息共享找到种群的最优解.假设一个种群由N个粒子组成,且在D维空间中进行搜索,则第i个粒子速度和位置的更新公式可表示为:
(18)
(19)
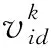
3.3 改进粒子群算法
传统的粒子群算法具有收敛速度快,原理简单,容易实现等优点.但配电网故障重构是多峰优化问题,在后期寻优过程中易陷入局部最优,出现种群多样性降低和收敛性差等问题.针对上述问题对PSO做出以下改进.
3.3.1 Sin混沌初始化种群
由于混沌映射具有遍历性和随机性等特点,在初始化种群时,可以利用混沌映射来增强初始种群的多样性及均匀分布性,保证算法初始寻优的精度与效率.而Sin混沌映射相比Logistic混沌映射更具有混沌特性[16].因此文章采用Sin混沌映射初始化种群,其表达式如下:
(20)
式(20)中:xn的取值范围为[-1,1],且初始值不能0.经过Sin混沌映射初始种群将遍布整个解空间.
3.3.2 融合收缩因子和Levy飞行策略
粒子更新过程中,主要由三个参数控制粒子的速度,即ω、c1、c2.ω大小决定原来粒子速度对当前例子速度的影响,c1、c2则代表对自我和社会学习的认知.c1越大粒子偏向局部搜索,c2越大则会更多的偏向全局搜索,因此需要对ω、c1、c2这三个参数进行合理的优化和限制.优化后的新速度表达式如下:
(21)
式(21)中:ω为动态自适应权重,φ为改进压缩因子,ω、φ的表达式为:
ω=ωmin+(ωmax-ωmin)×exp(-3.5×(k/maxgen)2)
(22)
(23)
式(22)中:ωmin为初始惯性权重,ωmax为迭代结束时的惯性权重,maxgen为最大迭代次数.
动态自适应惯性权重可以提高算法的计算效率,改进收缩因子可以对学习因子部分进行限制,保证学习因子不会过大和过小,提高算法的收敛性.然而在算法的迭代后期,粒子的搜索空间逐渐减小,容易陷入局部最优.针对以上问题在算法的后期引入Levy飞行策略,以此扩大粒子的搜索空间.其飞行位置表达式如下:
(24)
Levy(λ)=μ|v|1/β
(25)
式(24)~(25)中:α为步长控制参数,文章中取1;⊕符号表示点乘.式(25)为Levy飞行的近似公式,通常用Mantegna算法来模拟实现[17];μ和v服从正态分布,β取值为常数1.5.
3.3.3 融合柯西变异和反向学习策略
反向学习是Tizhoosh提出的一种新的方法,他是以当前全局最优解为基础,求其反向解,通过评估选择更合适的最优解.将反向学习引入到PSO算法中,其表达式如下:
(26)
(27)
b1=(1-k/maxgen)k
(28)
高斯变异和柯西变异是常用的两种扰动方式,柯西分步密度函数两端较长,相较于高斯变异,更容易跳出局部最优[18],故文章选择柯西变异提高算法的全局收敛性.柯西变异的表达式如下:
(29)
cauchy(0,1)=tan(r4-0.5)π
(30)
为了提高算法的寻优性能,将反向学习和柯西变异在一定概率Ps[19]下交替执行.
利用贪婪规则将扰动更新后与更新之前的全局最优值进行比较,通过比较新旧位置的适应度决定是否更新目标位置.其表达式如下:
(31)
3.4 基于改进粒子群算法故障恢复重构策略
图2为基于改进粒子群算法的故障恢复重构的流程图,基本步骤如下:

图2 配电网故障恢复重构流程图
(1)在故障恢复重构的过程中要确定可投入联络开关的位置,如果孤岛内边界负荷节点可投入联络开关,则将孤岛内边界的节点从孤岛删除,通过主网恢复供电.
(2)将配电网的剩余非故障失电区域中的节点和支路进行重新编号.
(3)初始化改进粒子群算法的基本参数.
(4)利用Sin混沌初始化种群.
(5)利用式(19)、(21)进行初始位置更新,当粒子停留在局部迭代次数大于等于5时,利用Levy飞行策略扩大粒子的搜索空间.
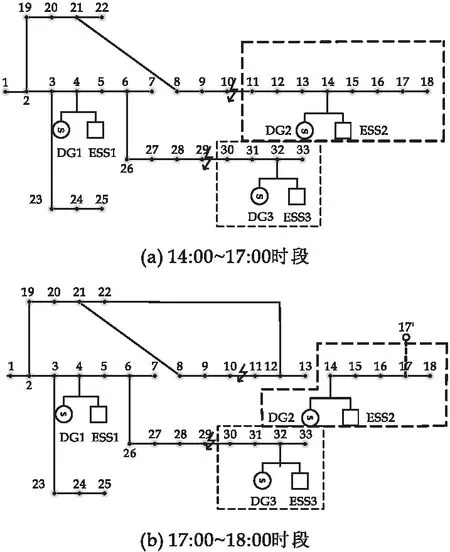
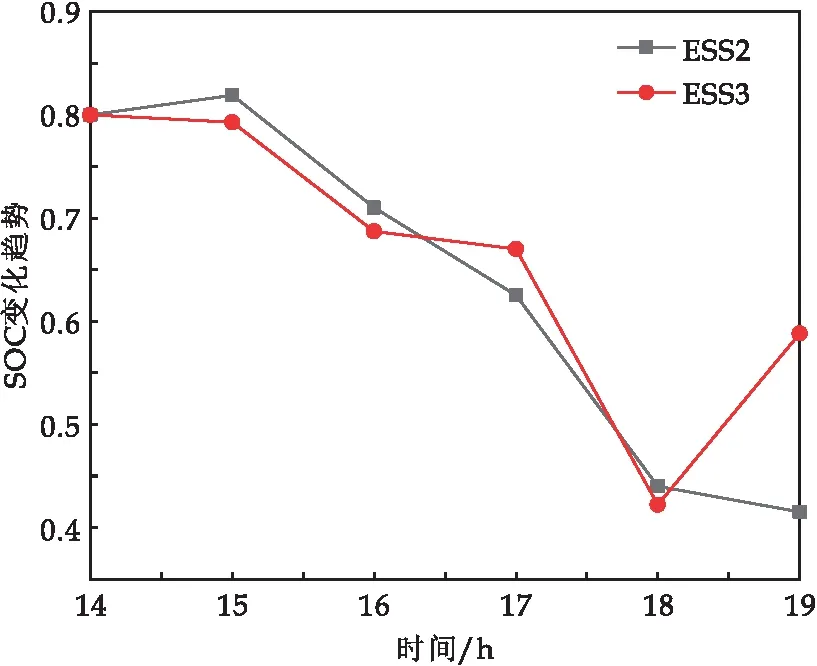
(6)对全局最优位置进行扰动,如果r4 (7)利用贪婪规则将新旧目标适应度对比,确定是否要对位置更新. (8)判断是否达到最大迭代次数,若达到条件则算法停止,输出故障恢复结果;否则返回步骤(5). 文章采用图3所示的IEEE 33配电网节点模型进行算例仿真,该系统的额定电压为12.66 KV,额定功率为3 715+j2 300 KVA,包含33个节点,37条支路.文章中每个节点的负荷类型可见表1所示,每个节点的典型日负荷需求可见文献[13].负荷优先级和可控负荷节点见表2所示,考虑到负荷削减可能对可控负荷本身产生一定的影响,对可控负荷的削减最多占整个负荷的20%.在节点14接入光储系统,节点4、32接入风储系统,储能装置的初始SOC为0.8,最大、最小SOC为0.95和0.25,具体参数可见表3所示.光伏和风机的日出力曲线见图4所示,其功率因数为0.85. 表1 节点负荷类型 表2 负荷优先级和可控负荷类型 表3 光储和风储系统参数 图3 IEEE33节点配电系统图 图4 光伏和风机日出力曲线 文章采用改进粒子群算法对剩余配电网进行恢复重构,其参数设置如下:粒子维度设为5,种群规模为30,在大迭代次数设置为100,惯性权重的最大最小值分别为0.9和0.4,学习因子为2. 设故障时刻发生在14∶00,故障持续时间为5 h,故障支路发生在10-11和29-30.14∶00~18∶00商业负荷需求处于高峰期,将商业负荷的时间尺度重要系数Dt设置为5,居民负荷Dt设置为1.在18∶00~19∶00时与之相反. 整个恢复过程中的14∶00~17∶00见图5(a)所示,17∶00~18∶00见图5(b)所示,18∶00~19∶00见图5(c)所示,储能SOC曲线变化见图6所示.故障恢复过程中一级负荷、二级负荷全部恢复,部分二级负荷通过对三级可控负荷的削减取得了优先恢复.由图6可发现,在14∶00~17∶00时间段内,负荷的恢复率为100%,可控负荷全部电力供应.而在17∶00~19∶00时间段,失电负荷的恢复率未达到100%.甚至18∶00~19∶00时间段内负荷节点30处于完全失电状态.因为17∶00~19∶00时间段,居民负荷需求量逐渐增大,同时光伏系统的出力值逐渐减小. 图5 不同故障时间的恢复结果 图6 储能装置的SOC变化曲线 4.2.1 不同方案下仿真结果 为了验证本文模型的有效性,文章采用三种不同的方案做对比,具体方案如下: 方案一:考虑风光荷的不确定性,只对配电网进行孤岛划分,不投入联络开关,即不考虑孤岛划分和重构之间的关系. 方案二:采用本文的故障恢复方法,不考虑不同类型负荷的时变需求,整个故障过程中的负荷取五个时段的平均值,不接入储能装置. 方案三:采用本文所提的故障恢复方法,考虑不同类型负荷的时变需求,整个故障过程中取负荷的实际出力值,储能装置根据负荷需求进行出力. 各种方案的故障恢复结果如表4所示,方案一和方案三对比可知,文章所提故障恢复方法的负荷恢复率为98.76%,优于方案一的95.81%.因为方案一中未投入相应的联络开关,未对剩余失电负荷、支路分析.方案二和方案三对比可发现,在考虑不同类型负荷的时变需求和储能优化出力的情况下,采用文章所提故障恢复方法的负荷恢复率为98.76%,优于方案二的93.80%,且方案三前3 h可将所有失电负荷恢复,方案二中前3 h存在失电负荷.方案三优于方案二是因为方案二没有考虑负荷时变需求,且没有接入储能.风-光-储联合出力可以缓解分布式电源出力不确定性,考虑不同类型负荷的时变需求则能提高风储和光储系统的利用率,使更多重要负荷得到恢复.文章采用两种不同的方案与方案三做对比,其结果表明方案三优于其他两种方案,验证了本文模型的有效性. 表4 不同方案下的故障恢复结果 4.2.2 不同故障恢复方法仿真结果 为了进一步验证本文模型的优越性,采用文献[13]的故障恢复方法与本文所提的故障恢复方法在相同场景下做对比,设置相同的参数,最大迭代次数为100,种群规模为30.其结果如表5所示.由表5可知,采用本文所提的故障恢复方法恢复的总电量为98.76%优于文献[13]的97.34%,且采用本文所提的故障恢复方法,一、二级负荷全部恢复,采用文献[13]的故障恢复方法,部分二级负荷处于失电状态.因为文献[13]的孤岛划分方法可能使电量较大的负荷被切掉,没有考虑到用户侧负荷的灵活特性.其次在考虑孤岛划分与重构的配合时,文献[13]虽然确保了孤岛内供电量达到最大,但没有充分发挥联络开关状态集的作用,部分失电负荷无法通过联络开关恢复供电.文章所提故障恢复方法无论在负荷的恢复率还是负荷的恢复价值都优于文献[13]的故障恢复方法,证明了文章所提故障恢复方法的优越性. 表5 不同故障恢复方法对比 4.2.3 不同算法性能对比分析 为了进一步突出改进粒子群算法的优越性,利用基本粒子群算法(PSO)、粒子群-遗传算法(GA-PSO)与改进粒子群算法(IPSO)对比分析.为公平起见,三种算法在同一条件下运行,最大迭代次数为100,种群规模为30,学习因子均为2,三种算法分别运行50次,运用MATLAB2021b版本完成仿真,以系统的有功网损最小为目标函数进行配电网重构,表6为各种算法求解时间、迭代次数、重构后网损和电压偏差的平均值. 由表6可知,IPSO算法的平均求解时间为0.38 s,优于PSO、GA-PSO算法的平均求解时间.IPSO和GA-PSO算法相比PSO算法网损都得到了一定的改善,但GA-PSO算法的平均电压偏差为1.23 pu,高于PSO和IPSO算法,且PSO和IPSO平均迭代次数均为15次,GA-PSO算法的平均迭代次数为54次,因为在粒子每次搜索过程中都会发生突变,导致迭代次数过多.采用IPSO算法重构后配电网的网损和电压偏差得到了一定改善,同时IPSO算法也兼顾了故障重构过程的快速性.综上分析文章中所提的算法(IPSO)优于其他两种算法,体现了IPSO算法的优越性. 本文综合考虑风光荷的不确定性和负荷需求特性,从孤岛划分和网络重构两方面研究配电网故障恢复,得到以下结论: (1)本文构建风-光-储联合出力系统,并对负荷精确划分,能够缓解风光荷的不确定性对孤岛划分带来的影响.文章充分利用可控负荷的灵活特性,不仅使得重要负荷优先恢复,同时也减少了整个恢复过程中的负荷失电量. (2)本文将孤岛划分与网络重构技术相结合,充分利用联络开关状态集,更广域的失电负荷得到恢复. (3)本文采用IPSO对剩余区域进行重构,进一步恢复失电负荷,与其他算法相比,配电网的网损、电压偏差得到了一定的改善,且兼顾了恢复过程的快速性,避免陷入局部最优.4 算例分析
4.1 系统参数


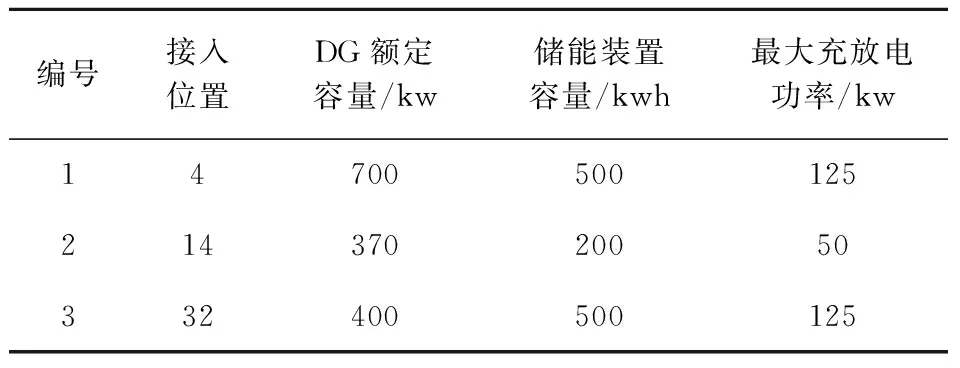

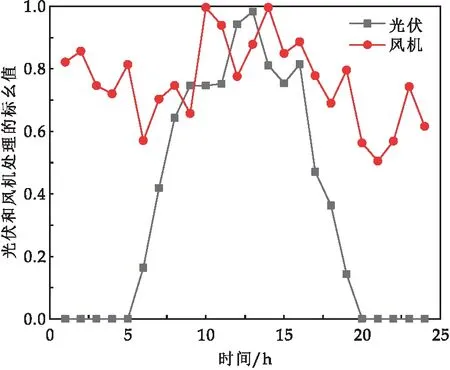
4.2 仿真结果



5 结论
