基于多场耦合模型的GIS断路器温度场仿真分析

2023-10-16陈邦发谢志杨潘英杰杨瑞明

陕西科技大学学报 2023年5期

陈邦发, 贺博, 谢志杨, 潘英杰, 杨瑞明

(1.广东电网有限责任公司佛山供电局, 广东佛山 528000; 2.西安交通大学电力设备电气绝缘国家重点实验室, 陕西西安 710049)

0 引言

作为高压输电网的主设备,GIS的可靠性直接影响着高压输、变电系统的整体稳定性[1].运行数据表明,母线连接处、隔离开关动静触头处及断路器触头部位是容易形成异常过热点并引发设备异常温升的部位,其中以采取动连接的断路器部位最为常见[2].当动静触头在接触圆周处因受力不均匀导致同轴度偏移,接触压力变化将引起局部接触电阻增大,触头部位温度逐渐上升,触头表面接触电阻进一步增大,接触劣化呈现正反馈加速,最终导致异常发热故障发生.因此及时掌握GIS设备温度场分布规律,建立壳体温度分布和异常发热之间的联系,对于先期发现故障,指导设备运维具有重要的工程价值.

针对GIS设备热流场分布规律,国内外开展了大量有限元仿真,研究由二维模型单一物理场向三维模型多场耦合演变.近年来,国内外学者采用多物理场耦合的方式,仿真结果更加准确.但是多数学者的研究模型较为简单,多集中于母线、隔离开关、绝缘盆子.且对于模型换流方式的考虑较为简单[3-7].以上研究多未考虑涡流损耗、集肤效应及GIS断路器内外同时存在的三种换热方式.研究都基于整体模型,尚未聚焦于到触头触指结构接触电阻变化对于温度场影响,无法准确模拟GIS触头过热性故障时温度场分布,电气触点(母线触头、隔离开关触头、断路器触头等)接触不良而引起的发热造成的故障占比极高,其中断路器触头接触不良又占此类故障的大部分[8],有必要进行深入研究.

本文以220kV GIS断路器为例,综合集肤效应、涡流损耗等热源形成因素,以及热辐射、热传导、热对流等传热因素,搭建了GIS断路器电磁场-温度场-气体流场的多物理场耦合模型.提出一种接触电阻等效法,模型精确至触头触指结构,可模拟不同电接触形态.对比分析GIS断路器不同排布方式、同轴度偏移对断路器温度分布的影响,为GIS断路器温度场分布规律研究提供重要参考价值.

1 模型建立

本文以220kV GIS断路器为研究对象,建立电磁-热流多场耦合有限元模型.

1.1 GIS断路器三维模型建立

考虑到在GIS设备内部,相较母线连接部位及隔离开关部位,断路器部位由于采用动连接方式,在反复动作下更容易出现因电接触不良而导致的过热故障.因此本文选择以断路器触指部位为研究对象,研究其异常发热及热流分布模型.模型主要涉及部件包括:导电杆、动触头、静触头、屏蔽罩、绝缘母筒、壳体、直管导线、绝缘拉杆.

图1为断路器结构图,图2为适当简化后的三维模型图,从热场仿真计算量及影响因素角度综合考虑,主要对圆角、倒角,填充微小螺栓孔洞等进行了适度简化,而可能影响热场仿真结果的其余参数均严格按照实际尺寸进行建模.

图1 断路器结构图

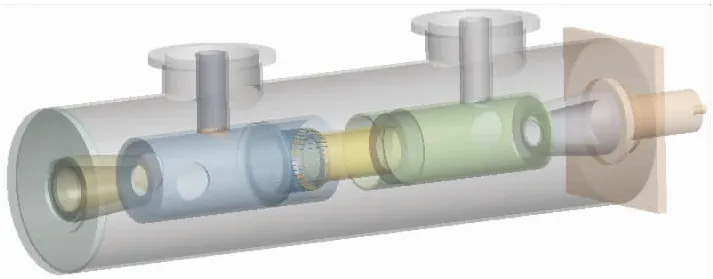
图2 断路器简化模型图

断路器模型中动静导体、触头、壳体等部件采用铝合金材质,绝缘母筒采用环氧树脂材质,气室内部填充SF6气体,表压0.5 MPa,根据具体材质选用不同的理化参数如表1所示.

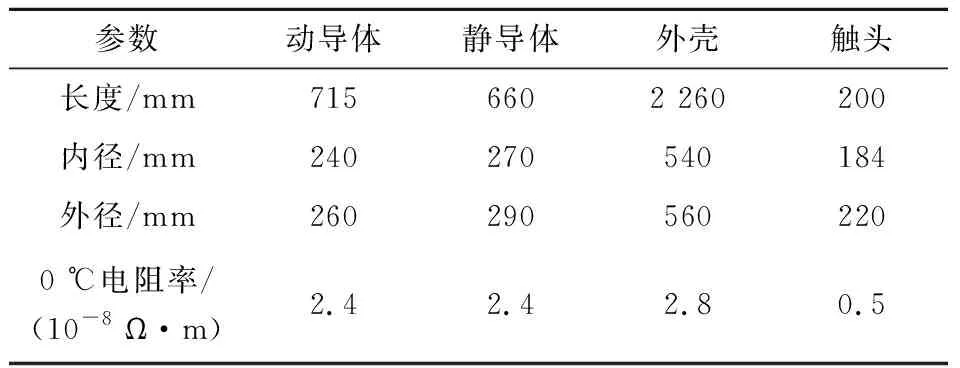
表1 断路器基本结构参数与材料参数

在触指部位采用36片导电触片并联结构进行建模,依据其导电原理,动静触头之间的等效电阻如式(1)所示:

Rc=Rj+Rb+Rm1+Rm2

(1)

式(1)中:Rj为接触电阻等效电阻;Rb为触指体电阻;Rm1为动触头体电阻;Rm2为静触头体电阻.图3为其触头连接处模型等效图.

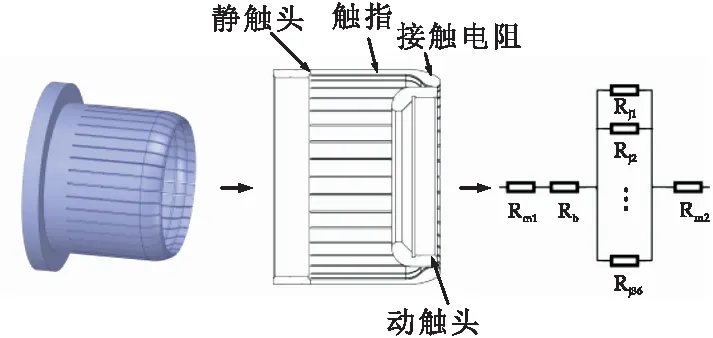
图3 触头连接处模型等效图

本文以自力型触头为研究对象进行建模,自力型触头依靠自身弹性形变产生的反作用力来实现动静触头之间的连接.自力型触头接触电阻较小,正常接触状态下每一片触指接触电阻一般在100 μΩ以下[9].但由于GIS断路器通流较大,接触电阻引起的热源在进行温度场分析时不可忽略[10].

在仿真模型中每个触指与动触头连接处建立厚度为4.3 mm触片.该触片为接触电阻的等效模型,将接触点处的接触电阻发热功率加载到此等效模型上进行温度场仿真,该触片体积电阻等效为此接触面的接触电阻.在温度场仿真中,通过改变触片电导率,可实现模拟接触电阻的改变,细化模拟不同运行工况.

1.2 三维电磁场计算模型

当GIS施加工频载流,设备内部将产生交变磁场,设备外壳因电磁感应产生感应电流,引起涡流损耗.故涡流场由麦克斯韦方程组表述如下[11,12]:

在整个求解域Ω内:

(2)

在涡流区(GIS 设备外壳)内:

(3)

GIS设备主导体总电流密度为:

(4)

单位体积生热率为:

(5)

接触电阻的发热功率计算公式为:

Pi=I2Ri

(6)

式(6)中:Pi为接触电阻发热功率;I为通过触片的电流;Ri为接触电阻.

1.3 传热及换热模型

当GIS断路器导体加载电流后,部分电磁能将转变为焦耳热,故设备温度场分布将随热传递过程发生变化.在通流初始阶段,GIS断路器导体温升速率较快,同时热量将由高温导体传递至低温SF6与外壳,因此断路器整体温度升高.由于外壳温升后与空气产生温度差,热量将以对流和辐射的方式发散至空气,故导体温升速率逐渐减慢[13].当断路器温度达到稳定,此时进入热平衡状态.

如图4所示,GIS断路器中的热流在热平衡状态下主要有三条路经[14,15]:(1)设备载流后,主导体产生欧姆损耗,外壳因电磁感应产生涡流损耗,热量以热传导方式逆温度梯度经固体路径传递至设备表面;(2)断路器导体、SF6、外壳、空气间存在温度差,故热量以对流方式在固体和气体间传递;(3)断路器温度高于绝对零度,热量以热辐射方式传递,其中导体温度较高,故辐射能量较大.

图4 GIS热传递过程示意图

由于热源和散热是决定断路器温度场分布的两大因素,故热传递控制方程由傅里叶微分方程表示:

(7)

式(7)中:T为温度,qv为热源强度,ρ为材料密度,k为热传导系数,c为比热.

1.4 边界条件及仿真步骤

涡流场的计算中,本模型中的电介质位移电流引起的发热程度很小,亦不会对导体的散热造成影响,所以导体与外壳之间的泄漏电流可以忽略,导体中电流只沿导体轴向流动.在导线端面施加频率为50 Hz,I=3 150 A电流,施加边界条件,设置涡流效应,以得到涡流场仿真结果.

规定涡流场边界条件[16]如下:

(1)假定空气域外边界与GIS设备外壳之间的距离无限大,空气边界磁场衰减为零,即:

A|ΓH=0

(8)

(2)ΓB为对称边界,该边界面上法向分量的磁感应强度为零,即:

Ay|ΓB=AZ|ΓB=0

(9)

(3)在导体和空气域端面设置磁力线平行边界,不考虑设备内部电介质位移电流及泄漏电流的作用.

涡流场中仿真计算得到导体功率损耗为298.823 W,外壳功率损耗为15.371 4 W,将二者作为热源载荷导入Fluent中进行计算.对GIS断路器的热分析做出如下假设:

(1)仅研究设备热传递的稳定阶段,不考虑各部分温度随时间变化的差异;

(2)各个材料参数为常数,不考虑因温度变化导致材料属性变化生成的迭代过程;

(3)GIS设备外壳、导体、绝缘筒材料属性参数为常数;

(4)考虑重力对SF6气体的影响,但不考虑温度变化导致SF6气体密度和体积的变化;认为外壳和空气的接触是整个设备结构唯一的散热途径.

本节采用电磁-流场-热场耦合的方式研究场域的温升问题,在仿真计算时假设GIS设备热量传递处于热平衡状态,且气体与导体之间为无滑移边界条件.设置环境温度为20 ℃,GIS断路器主导体、外壳、绝缘筒等部件材料属性参数为常数,气体设置为层流,设备外壳表面对流换热系数为6.3 W/(m2·K)不考虑SF6气体的辐射换热,重力加速度取g=9.81 m/s2,设置迭代次数为1 000.设置流体材料的性质参数如表2所示.

表2 流体材料的物性参数

温度场控制方程的边界条件要考虑物体边界与外界之间的能量平衡,根据GIS温度场多种换热方式及控制方程[17],设置边界条件说明如下:

(1)设置气体绝缘开关设备内部流固交界面和空气域外边界气体初始流速为0,即:

vx|Γ1,Γ2=vy|Γ1,Γ2=vz|Γ1,Γ2=0

(10)

式(10)中:vx、vy与vz为流体流速v的x、y、z轴分量.

(2)在空气域外边界设置初始温度:

T|Γ1=T0

(11)

式(11)中:T0为环境温度.

(3)GIS内部流体与固体、固体与固体交界面施加面-面辐射换热边界,即:

(12)

式(12)中:Fij为角系数;σs为Stefan-Boltzmann常数,取5.67×10-8;εe为表面发射率;Tt为GIS外壳温度;Tc为主导体温度.

(4)在GIS外壳表面施加大空间辐射换热边界,即:

(13)

2 热场仿真

气体流动因约束空间不同产生不同的热传导方式,水平放置的触头受重力及其他因素作用发生同轴度偏移导致接触电阻分布不均匀,以上因素均会改变GIS温度场分布.因此,分别探究了GIS不同排布方式以及水平排布时动静触头同轴度偏移对于温度场分布的影响.

2.1 仿真模型对比研究

本文建立的GIS断路器三维电磁-热-流耦合模型精确到单根触指,并引入接触电阻模型,能够更准确计算温度场结果,因此进行本文模型与传统模型的计算结果对比.设置负荷电流3 150 A,环境温度20 ℃,断路器横向摆放,设置触片接触电阻,得到不考虑接触电阻的传统模型和考虑接触电阻的本文模型的静触头温度分布云图如图5所示.

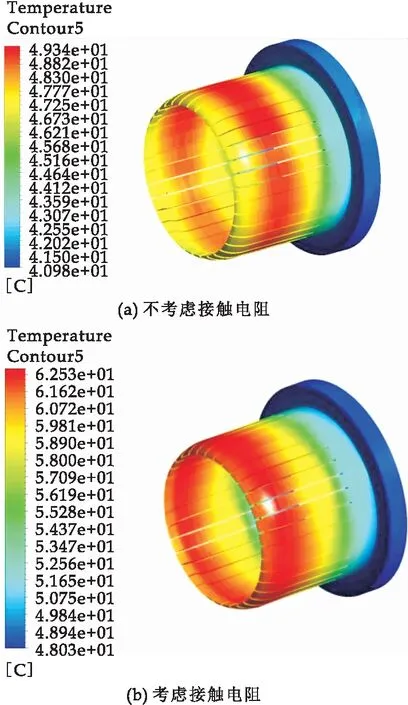
图5 接触电阻有无时静触头温度分布图

在涡流场中计算未考虑接触电阻的传统模型的导体功率损耗为227.449 W,外壳功率损耗为15.371 3 W,导体功率损耗较本文模型低71.374 W,导致传统模型静触头最高温度要低13.19 ℃.传统模型触头最高温度分布在触指中段,温度分布趋势与实际工况不符[8].由图5可知,本文建立的考虑接触电阻的计算模型能细化研究单根触指接触状态改变对温度场的影响.

2.2 不同现场排布热场仿真

在实际工程中,GIS设备有水平、竖直两种排布设计.由于SF6气体受热膨胀上浮以及具有自身重力,断路器排布方式将影响气体的流动方式,改变热传导状态,进而产生不同的温度分布.为研究摆放形态对GIS设备温度场的影响,保持其他条件不变,设置负荷电流3 150 A,环境温度20 ℃,模拟断路器竖直摆放(动端在上)、断路器竖直摆放(静端在上)两种形态.

当环境为20 ℃时,断路器横向摆放时温度场仿真结果如图6、图7所示.断路器外壳圆周数据点选取如图8所示,其中中间截面是水平排布的断路器触头最高温处对应的截面,0°点是中间截面上外壳温度最低的点.由图6、图7可知,断路器温度沿轴向温度呈低—高—低对称分布,动法兰处温度最低,为27 ℃左右;触头处温度最高,为62.33 ℃左右;外壳最高温为32.98 ℃左右.如图9所示,断路器中间截面处气体最高流速为0.166 m/s,且由于热空气上浮,气体流速最大值出现在截面最上方,在截面处SF6的对流散热效果较为明显,因此不可忽略SF6气体流动对GIS设备温度场分布的影响.

图6 导体温度场分布图

图7 外壳温度场分布图

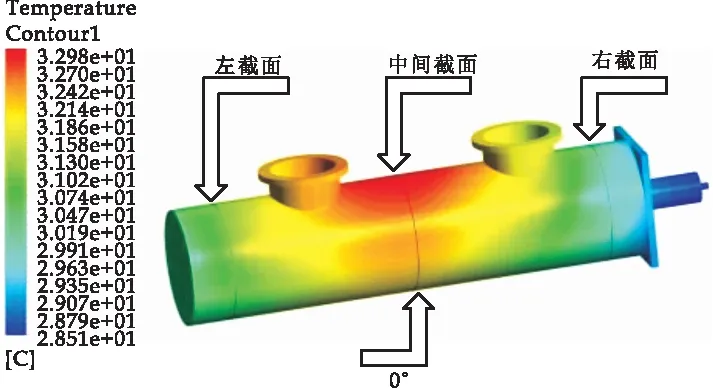
图8 断路器外壳圆周数据点选取图

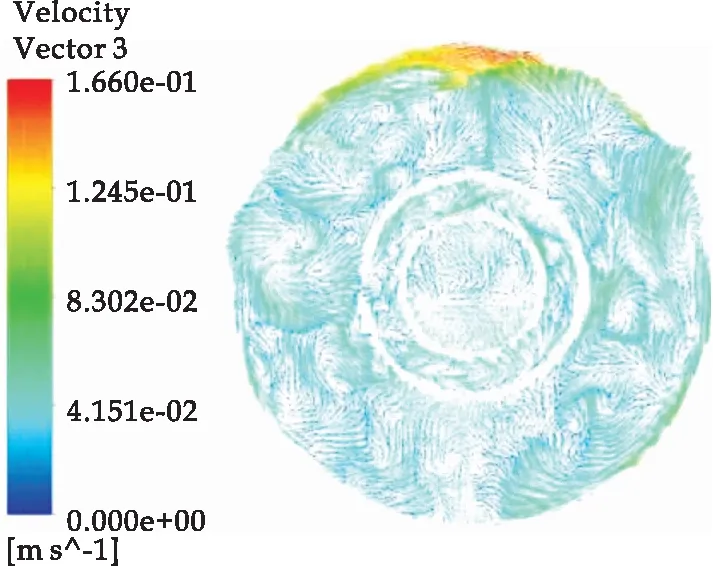
图9 断路器中间截面SF6流速矢量图

当断路器竖直摆放(动端在上)时,导体触头最高温度为60.60 ℃,外壳最高温度为31.34 ℃.由于断路器内部气体受热上浮,与水平摆放相比,动法兰温度更高,外壳的最高温度不再出现在触头对应的位置,而是向上偏移,但受到SF6气体传热性的限制,偏移量较小.仿真结果如图10所示.

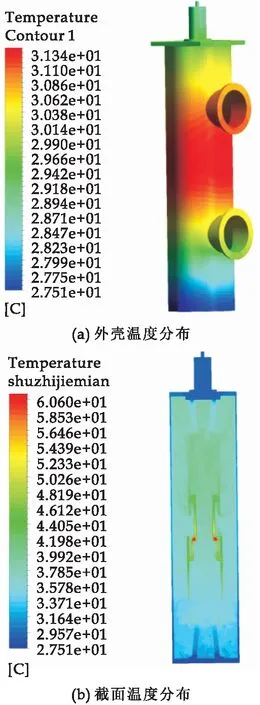
图10 竖直摆放(动端在上)温度场分布图

当断路器竖直放置(静端在上)时,外壳最高温度为31.24 ℃,导体最高温度依然位于触头处,为59.46 ℃,但由于内部气体流动方向发生了变化,此时外壳最高温度不再位于中部,而是向上偏移,静端温度显著增加.仿真结果如图11所示.

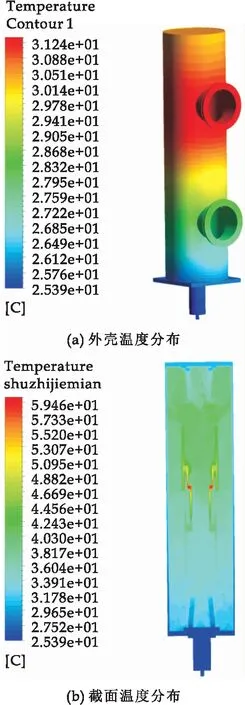
图11 竖直摆放(静端在上)温度场分布图

2.3 同轴度偏移热场仿真

由于金属构建在外力作用下蠕变,金属材料在应力大小、环境温度等因素下应力松弛,动静触头将发生同轴度偏移,引起接触圆周处受力不均匀,进而引起触片接触电阻局部增大导致异常温升[18].当触头接触电阻阻值相同,相较竖直排布,水平排布温升更大,且固定约束需承受传动机构自身重力产生的转矩,更易发生故障,故以水平排布时的自力型触头为例.断路器动静触头通过36片触指相连形成导电回路,在研究同轴度偏移对温度场影响时,将36片触指整体分为轻微接触不良、接触不良、接触良好、轻微受压、受压五部分来模拟实际存在的偏心故障工况.设置环境温度为20 ℃,忽略光照及风的作用[19],分别设置不同的接触电阻进行仿真分析,建立触头仿真模型如图12所示.不同偏移程度下,温度场仿真的关键参数设置及结果如表3所示.

表3 不同偏移程度对温度场分布影响

图12 考虑同轴度偏移的触头仿真模型

动静触头发生偏心故障后,圆周处接触压力不再相同,偏移程度越大,接触压力差值也就越大.运行工况下水平摆放的断路器,触指连接处由于常年受到重力影响,容易形成下端受压、上端接触不良的不正常接触状态.分别设置动静触头轻度偏心、中度偏心、重度偏心,来研究不同偏移程度的影响.在接触允许的范围内,接触压力越大,接触电阻越小[20].涡流场仿真计算中触指电流密度分布并不均匀,电流密度最小值出现在接触不良处,为1.548 9×105A/m2,最大值出现在受压触片处,为2.346 3×106A/m2.图13为同轴度轻度、中度以及重度偏移时,触头温度的分布图.由图13可知,随着偏移程度的增大,触头温度显著上升,温差逐渐增大.受压触片温度更高,容易形成局部过热点.

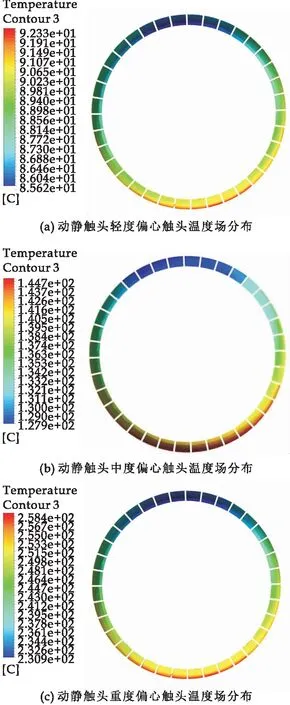
图13 同轴度不同偏移程度的温度场分布

3 仿真结果分析

基于以上仿真结果,本章将对排布方式、同轴度偏移引起异常温升的规律及机理进行深入分析.

3.1 排布方式对异常发热影响

在断路器外壳上选取如图8所示的中间截面,以水平摆放圆周温度最低点为0 °起始点,顺时针旋转一周,以旋转角度为横坐标,以温度为纵坐标,得到水平摆放不同截面外壳温度如图14(a)所示.得到水平摆放、竖直摆放(动端在上)、竖直摆放(静端在上)三种摆放形态圆周温度分布规律如图14(b)所示.

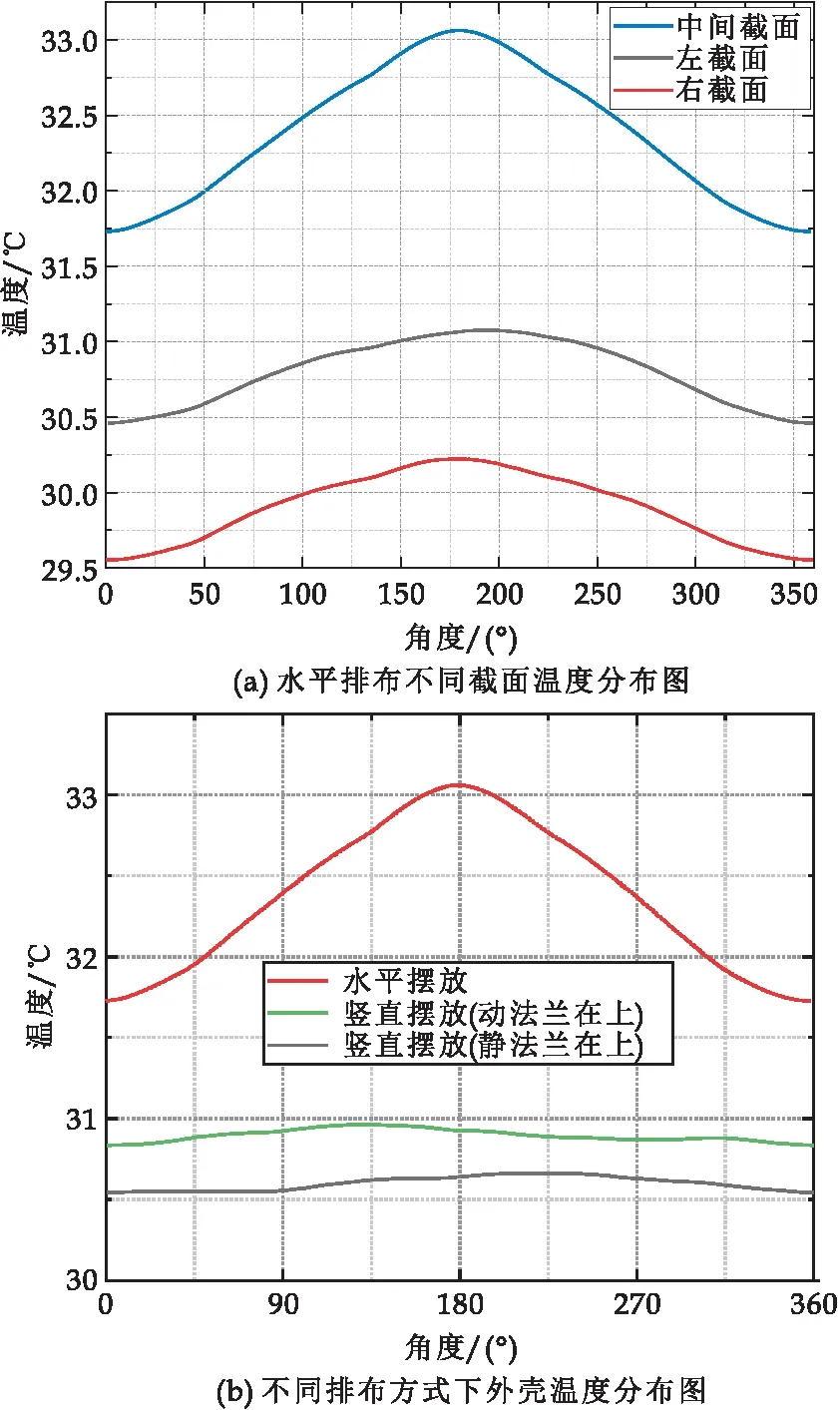
图14 不同排布方式下外壳温度分布规律图

由图14可知,水平摆放时沿GIS外壳圆周温差最大,而竖直排布时温度变分布较均匀.当断路器水平摆放时,SF6气体受热膨胀上浮,所以外壳圆周温度呈现上高下低、左右基本对称的分布规律,温升和温差都较大;而当断路器竖直摆放时,气体流动方向改变,圆周温度分布趋于均匀,几乎没有温差,整体温度偏低.

3.2 接触电阻对异常发热影响

为探究不同排布方式下接触电阻对温度场分布的影响,使接触电阻从9 μΩ增长至69 μΩ.如图15所示,触头最高温度随之线性上升,而断路器横放与竖放时的触头温升之差也随接触电阻的增大而增大.接触电阻每增加10 μΩ,触头最高温度上升约20 ℃.相同接触电阻时,断路器水平排布时触头温升最高,静法兰在上的竖直排布方式触头温升最低.因此断路器水平排布时更容易出现故障.

图15 不同排布方式下接触电阻对触头最高温度的影响

如图16所示,当热能以对流和辐射的形式进一步传递至设备壳体,外壳温升随接触电阻增大而增大.如图17所示,SF6气体受热上浮,而断路器水平排布时气体对流空间相对竖直排布时有限,故热量积聚于触头上方壳体处,因此外壳横、竖排布方式下的最高温温差随外壳温升逐渐加大.

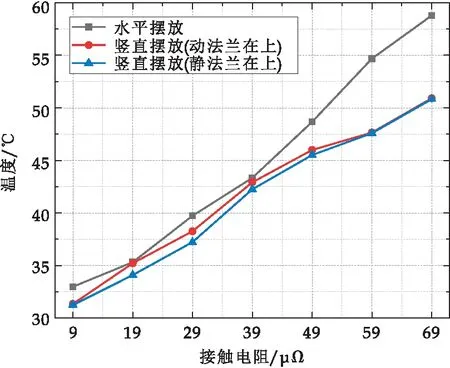
图16 不同排布方式下接触电阻对外壳最高温度的影响

断路器水平和竖直两类不同排布方式,相同接触电阻条件下:接触电阻小于49 μΩ时,断路器排布方式对触头和外壳温度影响较小.接触电阻大于49 μΩ时,水平排布方式下对流空间有限,触头和外壳温升明显高于竖直排布方式.

设置触片所在位置为坐标原点,断路器轴线为一维坐标轴,方向由静法兰指向动法兰,如图18所示.断路器竖直放置时,随着接触电阻从9 μΩ增长至69 μΩ,SF6气体温度上升,对流效果变强,故外壳最高温度点从触头处逐渐向法兰偏移,即沿断路器轴线向气体重力加速度反方向移动,如图19所示.

图18 断路器一维坐标示意图

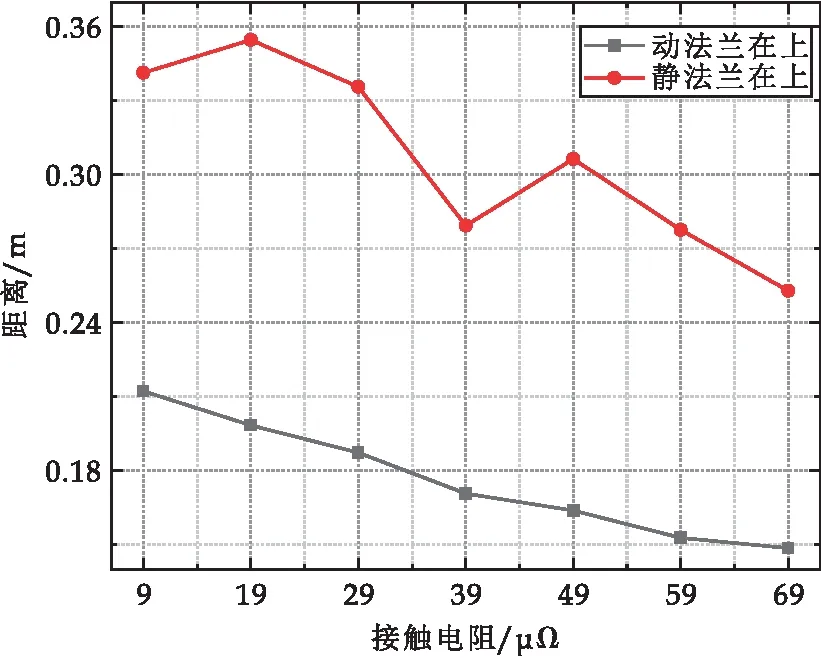
图19 最高温度点与坐标原点相对距离

3.3 同轴度对异常发热的影响

水平排布的断路器,当触头发生偏心故障时,触指接触压力不等,接触电阻值分布不均匀,故电流集中于少数触指处.如图20所示,偏移程度越大,触片所受压力越大,导体局部温升越高,在同一截面圆周内温差越大.

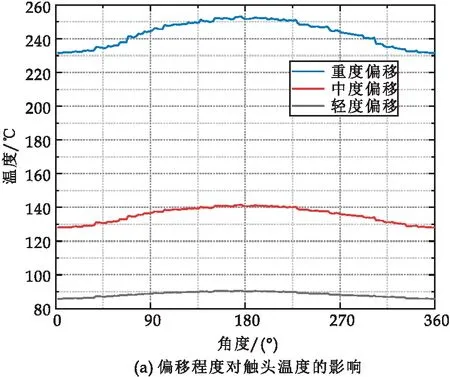
图20 偏移程度对温度场分布的影响

发生同轴度偏移时,触头和外壳温度均较正常状态下出现明显的升高.选取不同偏移程度时中间截面180 °点的触头及断路器外壳温度.中度偏移与轻度偏移时温度作差,重度偏移与中度偏移之间温度作差.触头温差分别为50.52 ℃和111.05 ℃,外壳温差分别为11.27 ℃和55.87 ℃.偏移程度的劣化,对断路器内部触头温升影响更大.在水平排布时,断路器下部触片受压,温度更高,但是热SF6气体上浮与上部外壳对流换热,导致中间截面正上方点的外壳温升最高,此点为GIS断路器水平排布时,最佳外壳温升监测点.