高维尾期望回归模型分布式估计方法的改进

朱 霞，潘莹丽

（1.中南财经政法大学 统计与数学学院，武汉 430073；2.湖北大学a.数学与统计学学院；b.应用数学湖北省重点实验室，武汉 430062）

0 引言

分布式计算的主要特点是对海量数据进行分布式数据挖掘。在分布式系统中，不同的机器之间需要数据的传输。在主从模式的分布式系统中，研究者普遍关注且不可避免的一个问题是由Master 和Worker 之间信息传输所导致的沟通成本问题。为了降低沟通成本，一种常用的方法是Zhang 等（2013）[1]提出的one-shot 方法。该方法让每个Worker先根据自己的数据得到一个比较好的估计值，再把每个估计值由不同的Worker传递给Master，然后Master将各个Worker 传递过来的估计值求平均得最到终的估计量。one-shot 方法只需进行一轮主从机器之间信息的传输，且传输的仅是一个向量。然而，该方法为了使平均估计量达到一定的收敛速度，要求每个机器必须获得至少个样本，机器的数量必须比小得多[2,3]。Jordan 等（2019）[4]提出的基于交互有效的替代损失（CSL）函数的分布式学习方法较好地克服了one-shot 方法的缺点。在频域框架中，CSL函数可以像全局损失函数一样用于形成点估计或进行统计推断，且在有限次的沟通次数下，基于CSL 函数的估计量与基于全局损失函数的估计量具有相同的收敛速度。借鉴构造CSL函数的思想，Pan（2021）[5]和潘莹丽等（2022）[6]分别基于大规模高维尾期望回归模型和大规模Huber 回归模型给出了一个沟通有效的分布式优化方法。然而，这两篇文章给出的解决方案只是每个Worker 仅计算梯度，由Master 求解优化问题，从而导致Master 一直在工作，而其他Worker 在空转。因此，在主从分布式架构下，如何避免将任务集中于Master 一台机器，进而研究如何改进分布式优化方法非常必要。

受交互有效的替代损失（CSL）函数的启发[4]，本文基于尾期望回归模型提出一种广义替代损失函数——梯度增强型损失（GEL）函数，能有效避免CSL函数导致的Worker空转而Master一直工作的局面。为了对参数进行估计和对变量进行选择，本文对GEL 函数施加平滑裁剪绝对偏差（SCAD）惩罚和自适应最小绝对收缩与选择算子（adaptive LASSO）惩罚[7,8]，并构造正则化梯度增强型损失（GEL）函数。由于Boyd等（2011）[9]指出交替方向乘子法（ADMM）算法适用于大规模统计推断和分布式凸优化问题，故为了对正则化GEL函数进行优化，本文还提出一种增广型极大交替方向乘子（Proximal-ADMM）算法。本文提出的方法运用正则化GEL函数，在计算上充分利用每台机器（Worker）的计算优势，加快收敛速度，使得所有机器（Worker）可以并行优化各自对应的GEL函数，然后传输到主机（Master）上对结果进行整合得到最终的估计。在沟通成本方面，本文将通过模拟和实证研究验证Proximal-ADMM 算法可以在有限轮Master 和Worker 之间的沟通中收敛于基于全样本（所有数据）的Centralize方法的结果。

1 高维尾期望回归模型分布式估计的改进过程

1.1 高维尾期望回归模型

其中，xi是p维协变量；β0(τ)是p维参数；εi(τ)是随机误差项，满足给定xi，εi(τ)的第τ个尾期望为零。为了便于表示，以下将β0(τ)和εi(τ)分别简记为β0和εi。假设参数真值β0是稀疏的，即若记Γ={k:βk0≠0} ，其中βk0是β0的第k个元素，q=|Γ|是集合Γ 中元素的个数，则稀疏假设意味着q≪p。在大数据背景下，受单机存储性能的制约，很难将全样本存储于一台机器之中。在主从分布式架构下，将数据随机均匀存储是解决单台机器存储瓶颈的重要方法。不妨设样本总量N=nm，即有m台机器，每台机器随机存储n个样本。记第j台机器上的观测数据为，则所有样本可被记为：

定义基于全部观测数据的全局损失函数如下：

其中，ρτ(u)=τu2I(u＞0 )+(1 -τ)u2I(u≤0 )是尾期望回归中的凸损失函数。类似地，定义基于存储在第j台机器上数据的局部损失函数如下：

在大数据背景下，为了同时达到参数估计和变量选择的目的，若直接最小化正则化的全局损失函数QN(β)将产生较高的计算成本，且对单机的性能要求较高。因此，寻找全局损失函数的一个替代损失函数，将是解决单机存储瓶颈和单机计算耗时耗力的有效方法之一。

1.2 正则化梯度增强型损失（GEL）函数

为了构造全局损失函数的一个替代损失函数，将QN(β)在任意初始估计量处进行一阶泰勒展开得：

以下将替代损失函数Q(β)称为GEL函数。

Jordan等（2019）[4]将R(β)替换成基于第1台机器上数据的R1(β)，并提出交互有效的替代损失（CSL）函数如下：

由式（6）和式（7）可知，GEL 函数更广泛，CSL 函数是GEL 函数的一个特例。在高维情形下，为避免过度拟合，提高模型的泛化能力，通常对GEL 函数施加一个惩罚项得到正则化GEL函数如下：

其中，pλ(·)是一个惩罚函数，λ是一个调优参数。以下考虑两种常用的惩罚：SCAD 惩罚和adaptive LASSO 惩罚。

对于SCAD惩罚，其惩罚函数形式为：

其中，a＞2，λ＞0。Fan和Li（2001）[7]建议取a=3.7，可通过交叉验证的方法选择最优参数λ。Zou 和Li（2008）[10]也提出SCAD惩罚函数可以做如下局部线性近似：

其 中，∇pλ( ×) 是pλ(·) 的 一阶导数，定义∇pλ(u)=，符号e+表示若e＞0 ，则e+为e，否则为零。结合式（8）和SCAD 惩罚函数的局部线性近似式（9），省略与参数无关的常数项，构建施加SCAD惩罚的GEL函数如下:

基于式（10），给出β的第一个估计量如下：

此外，本文将考虑adaptive LASSO 惩罚下参数的估计和变量选择问题。将式（8）中的惩罚项换成adaptive LASSO惩罚[8]，得正则化GEL函数如下：

1.3 增广型极大交替方向乘子（Proximal-ADMM）算法

为对正则化替代损失函数式（14）进行优化，现构建增广型Proximal-ADMM算法如下。

ADMM 算法通过将式（15）表示为以下的等效形式来解决：

其中，γ＞0 是调优参数，为增广项。根据凸优化理论，优化问题式（16）的拉格朗日函数为：

基于第j(j=1，2，…，m)台机器（Worker）上的观察值的优化目标函数L(β，z，θ)，ADMM 算法的迭代更新公式为：

其中，(βt+1，j，zt+1，j，θt+1，j)表示基于第j台机器（Worker）上的数据计算出的第t+1 次迭代值。省略与参数无关的常数项，式（18）可表述为：

式（19）中的z步存在一个显示解，且可以对z中的每个元素进行优化。事实上，对于i=1，2，…n，有：

其中，Proxρτ/nγ(·)为凸函数的近似点算子，定义如下：

对m台机器（Worker）上的更新值zit+1，j求平均得z步的第t+1次更新值为：

对于一般的设计矩阵，β步的更新没有显示解。对式（19）中的β步增加一项，得到如下修正的β步：

其中，V=γ(ηIp×p-xTx)，η≥Λmax(xTx)，Ip×p是p×p单位矩阵，Λmax(·) 表示对实对称矩阵取最大特征值，是由V定义的半内积诱导的半范数。通过计算，可得：

由式（22），修正后的β步可变为：

其中，j=1，2，…，m，x(k)表示设计矩阵x的第k(k=1，2，…，p)列。定义软算子Shrink[u，a]=sgn(u)(|u|-a)+，其中sgn(·) 是符号函数，通过简单计算，式（23）变为：

对m台机器（Worker）上的更新值βt+1，j求平均得β步的第t+1次更新值为：

同样地，对基于m台机器的式（19）中的θt+1，j取平均得θ步的第t+1次更新值为：

2 数值模拟

本文运用Proximal-ADMM 算法（简称Paverage 算法）与基于第一台机器所设计的分布式优化方法（简称Psingle算法[5]）和基于全样本执行原始的ADMM 算法（简称Centralize算法）进行模拟研究，来验证所提出的在SCAD惩罚和adaptive LASSO惩罚下尾期望回归模型的增广型Proximal-ADMM 算法的参数估计和变量选择结果的有限样本性能，以及其估计误差与主从机器沟通次数的关系。

考虑回归模型如下：

其中，协变量x1，x2，…，xp通过两个步骤生成。步骤1：生成，协方差矩阵Σ的第(ij)元σij=0.5|i-j|，i，j=1，2，…，p；参数维数p=300。步骤2：设定，其中Φ(·)是标准正态分布的累积分布函数。参数真值β6=β12=β15=β20=1，参数真值β的其余元素均取值为0。随机误差ε～N( 0，1)或ε～t(3)。样本量N=2000，将其随机均匀分配到m=20台机器（Worker）上，每台机器样本量n=100。考虑三个不同的尾期望值τ=0.3，0.5，0.7。将数据随机分成训练集（Dtrain）和测试集（Dtest），采用20 折交叉验证法，通过优化泛函来选 择参 数λ，其中为基于训练集的参数估计量。

通过100次模拟，可从以下几个方面比较上述Paverage、Centralize 和Psingle 三种方法的性能。分别给出SCAD惩罚和adaptive LASSO惩罚下的尾期望回归模型的参数估计和变量选择结果，如表1和表2所示。其中，Size为非零回归系数的平均值≠0(k=1，2，…，p)。P1为在模拟时包含所有真正非零回归系数的比例，即对于任何k≥1，估计值≠0且真实参数βk0≠0。P2为在模拟时选择变量x1的比例。ER为估计误差。在Size、P1、P2和ER的列中，括号内的数字是该列指标相应的样本标准差。

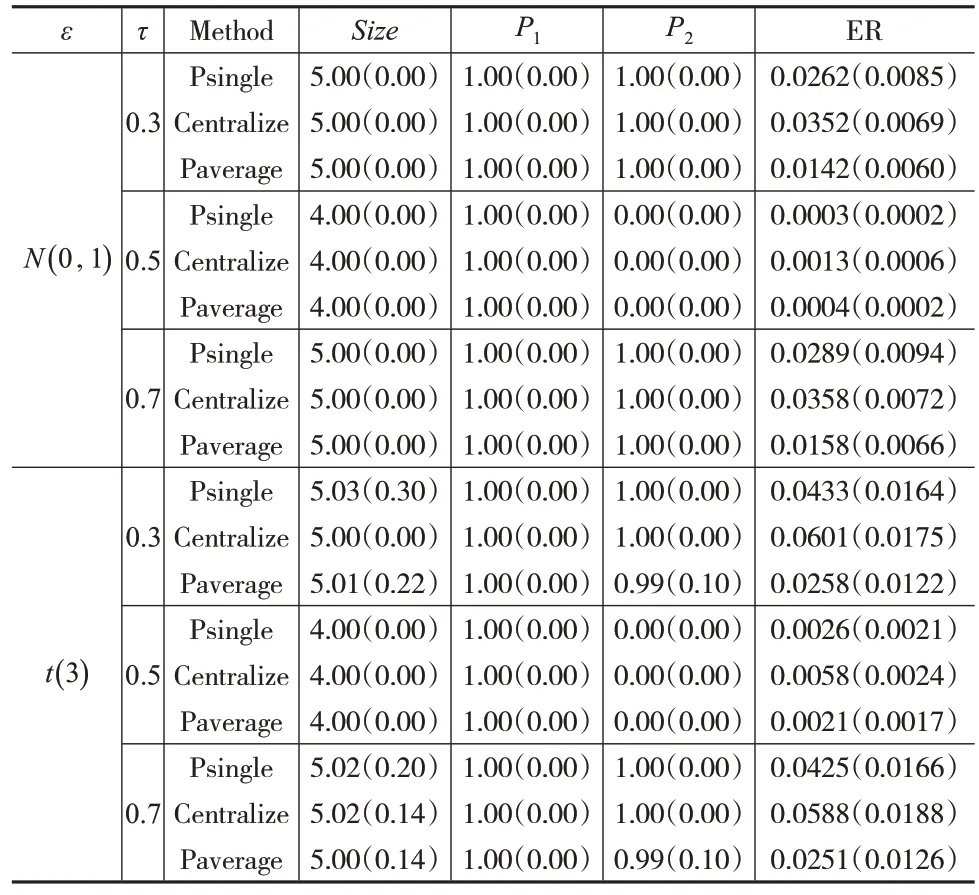
表1 SCAD惩罚下尾期望回归的模拟结果

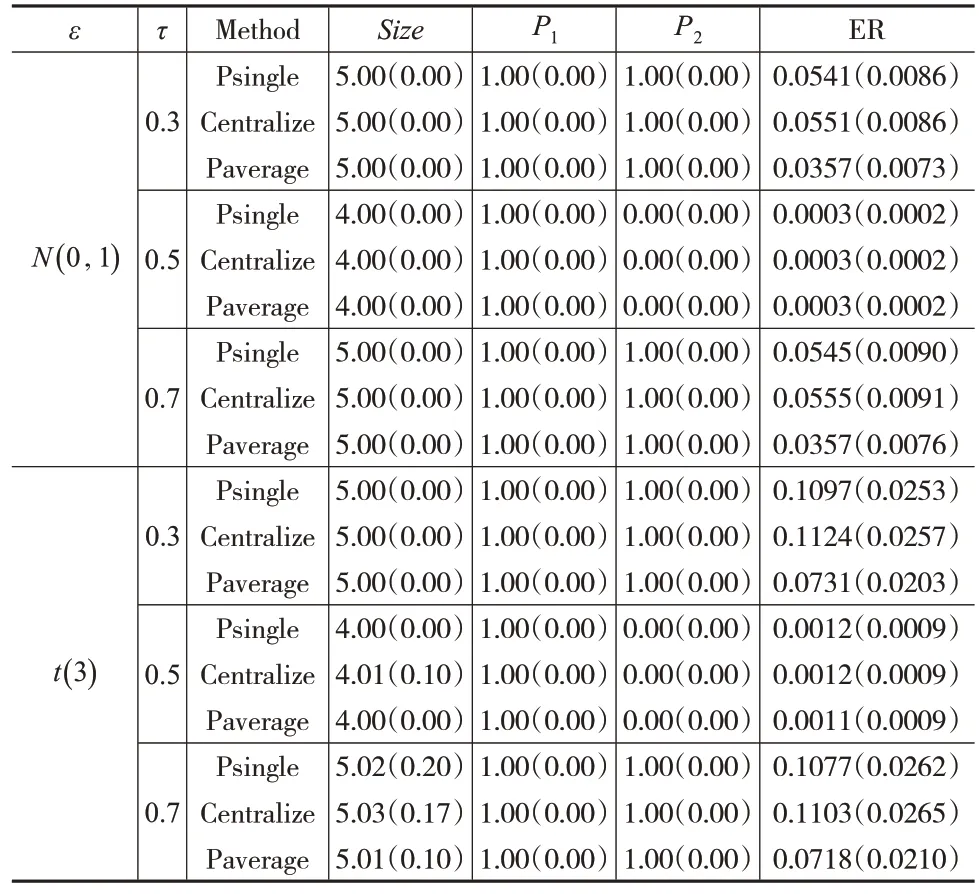
表2 adaptive LASSO惩罚下尾期望回归的模拟结果

表1中的结果显示，在参数估计方面，由Paverage方法和Psingle方法所生成的估计值可以与Centralize方法所生成的估计值相媲美。而Paverage方法的估计误差比Psingle 方法的估计误差要小。在变量选择方面，当τ=0.3 和τ=0.7 时，所有方法都成功地选取了5 个变量（x1、x6、x12、x15和x20），且有较高的选择概率P1。对于协变量x1，除了τ=0.5 外，所有方法都展示出很高的选择概率P2。表2中的结果同样显示了类似的结论。

为了证明所提出的Paverage、Centralize和Psingle三种方法是沟通有效的，本文模拟绘制出随沟通次数变化的估计误差趋势图，展示出施加SCAD惩罚的尾期望回归随沟通次数变化的估计误差趋势结果，如图1 所示。施加adaptive LASSO惩罚的图形和图1类似。

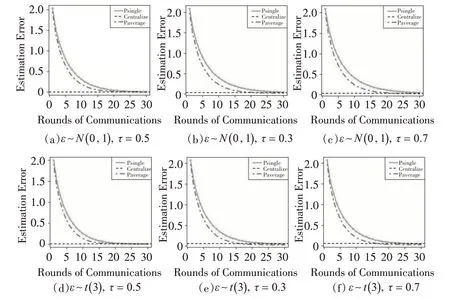
图1 SCAD惩罚下估计误差与主从机器沟通次数的关系

图1的结果表明，在经过数次主从机器（Worker-Master）之间的沟通后，所提的Paverage 方法的估计误差逐渐下降且趋近于Centralize 方法的估计误差。此外，相对于Psingle方法的估计误差，Paverage方法的估计误差收敛到Centralize 方法的估计误差的速度较快，表明基于GEL 函数的分布式优化方法相对基于CSL 函数的分布式优化方法在沟通有效方面具有更好的性能。

3 实证分析

本文将Paverage、Centralize和Psingle方法运用于人类免疫缺陷病毒（HIV）药物敏感性数据集的研究中，以验证所提出的方法在实际应用中的可操作性。该数据集从网站http://hivdb.stanford.edu中获取。研究人员指出，在未经治疗的艾滋病毒感染者中，每一个可能的单点突变每天发生104到105次，耐药性已成为艾滋病毒治疗的主要障碍。因此，了解突变对耐药的影响是一个重要的研究课题。本文将主要对药物efavirenz（EFV）敏感性数据进行分析。在排除一些罕见突变后，该数据集包括1472 个HIV 分离株和197 个突变位点。将对药物EFV 敏感性度量的自然对数作为响应变量，将197个突变位点作为协变量。由于病毒突变的位置通常非常稀少，因此可通过施加惩罚项来获得稀疏解。本文将建立施加惩罚的尾期望回归模型研究197个突变位点对药物EFV敏感性的影响。

采 用Paverage、Centralize 和Psingle 方 法 分 析HIV 数据并比较三种方法的性能。考虑三个不同的尾期望值τ=0.3，0.5，0.7 。将整个数据集随机分成两部分：训练数据集（Dtrain）和测试数据集（Dtest），样本量分别为1200和272。训练数据集在12 台机器上随机分割，每台机器随机存储100 个样本。基于训练集的1200 个样本，在最小化损失函数的基础上，采用12 折交叉验证法选择调优参数λ，然后利用测试集上的数据，通过PE=(1 272)计算预测误差，其中(λ)是由训练集得到的参数估计。重复上述过程20次，表3汇总了所选重要解释变量的预测误差，此外，列括号里的数表示其相应的样本标准差。从预测误差的角度来看，运用Paverage方法得到的预测误差均在合理范围内。

表3 用三种方法比较HIV药物敏感性数据集性能的预测结果

将在τ=0.5 下通过20次随机分割后各种方法选择的重要变量的频数汇总到表4 中。τ=0.3，0.7 的结果与τ=0.5 类似。从表4 可看出，除了个别基因，使用adaptive LASSO 惩罚的Paverage 方法选择的变量结果与Centralize方法选择的变量结果高度一致。总而言之，这些结果表明，在艾滋病毒药物敏感性数据集研究中，本文提出的方法在变量选择和预测性能两个方面均有很好的效果。

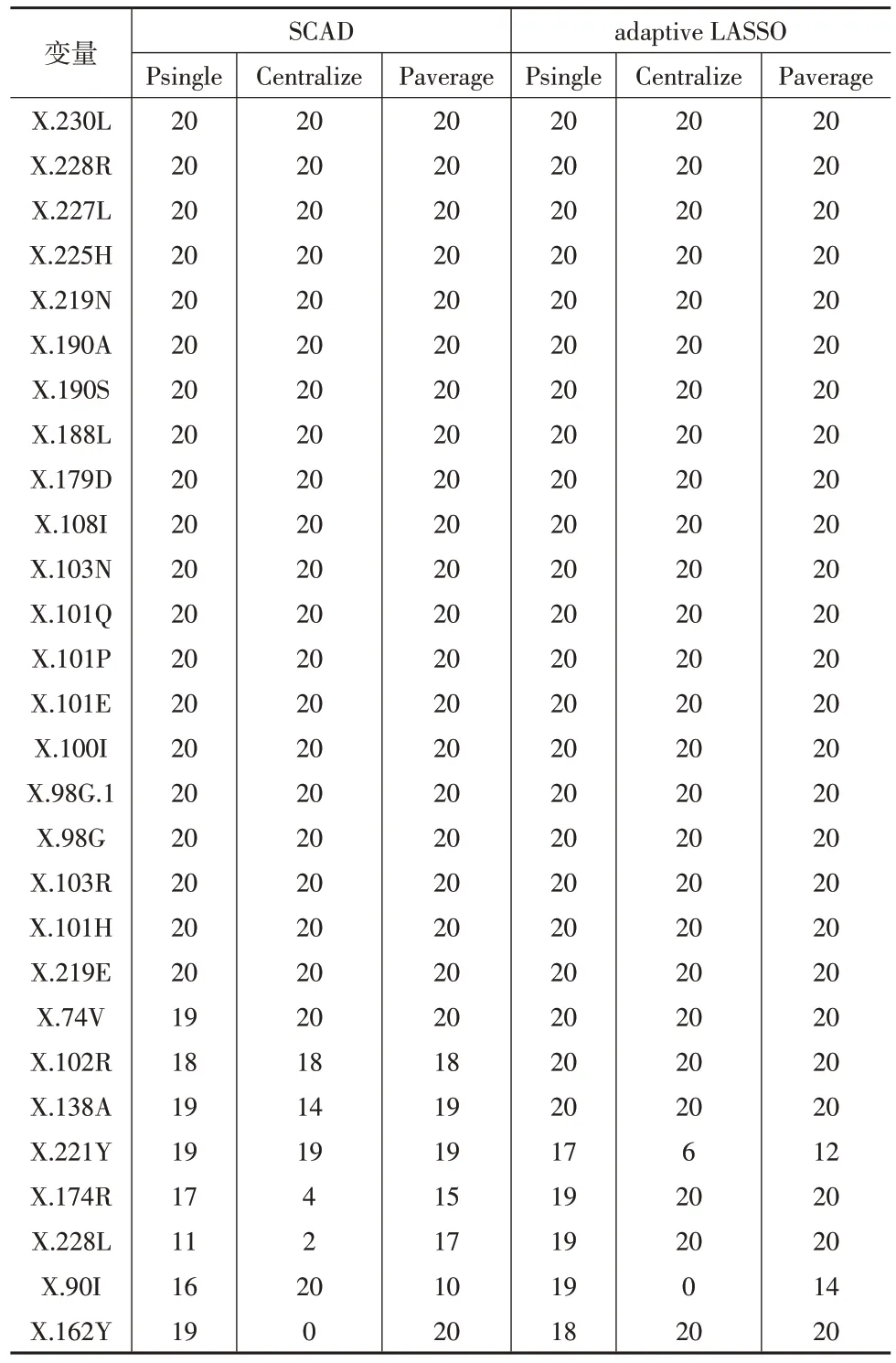
表4 用三种方法比较HIV药物敏感性数据集性能的频率表（τ=0.5）

4 结论

在主从分布式架构下，本文通过施加SCAD 惩罚和adaptive LASSO惩罚提出了施加惩罚的大规模尾期望回归模型。为了降低机器之间的沟通成本，本文又构造出一种新的全局损失函数——沟通有效的GEL函数。然后本文将基于全局损失函数的高维正则化估计问题转化成了基于沟通有效的GEL函数的高维正则化估计问题。为了优化施加惩罚的GEL 函数，本文还提出了增广型Proximal-ADMM算法，在计算上，在Worker机器上计算估计量和在Master机器上整合估计量交替进行，进而加快了算法的收敛。在主从机器之间的沟通成本方面，经过了几轮机器之间的沟通后，本文提出的Paverage方法的估计误差收敛于Centralize 方法的估计误差，相对于Psingle 方法的估计误差，Paverage方法的估计误差收敛到Centralize方法的估计误差的速度较快。数值模拟和实证分析的结果表明，本文提出的方法在样本量有限的情况下具有良好的性能且在实际应用中具有可操作性。