混合样本下双因素误差模型的参数估计

刘 鑫，王维国，薛 景，李 飒

（1.辽宁石油化工大学a.理学院；b.经济管理学院，辽宁 抚顺 113001；2.东北财经大学 经济学院，辽宁 大连 116025）

0 引言

在计量分析领域，面板数据具有控制个体异质性、可研究动态调整过程等优点，然而在抽样调查领域，抽样框覆盖不全、调查个体不回答、大量调查样本流失等问题日益突出。轮换面板数据因其每期有新个体的加入，可有效缓解普通面板数据存在的问题，已被广泛应用于市场调查、民意调研及教育经济等众多领域，人们对轮换面板数据的关注度也越来越高。而轮换面板数据的每期调查需要找寻新个体的参与，与普通面板数据相比，调查成本不断增加[1]。鉴于普通面板数据与轮换面板数据各自的特点，为了充分利用样本各自的优点，常考虑将普通面板与轮换面板数据结合得到混合样本来推断总体。如果将混合样本假设为普通面板或轮换面板数据，使用单独样本下的极大似然估计方法，会低估或高估未知参数估计量的方差，普通面板或轮换面板数据下的极大似然估计方法不再适用于混合样本。因此，如何利用混合样本来估计总体，是统计推断所面临的一个挑战性问题。目前，迭代极大似然估计已被广泛应用到非平衡面板数据中[2]，本文提出的混合样本属于一类特殊的非平衡样本，由于部分平衡样本的存在，直接使用非平衡面板数据下的迭代极大似然估计会产生较大偏误，因此也不能直接将这种方法用于混合样本。另外，目前大量基于混合样本的研究发现，与单一样本相比，混合样本在各类研究过程中更具有普适性，同时也给出了混合样本下不同的估计方法[3,4]。受此启发，本文将现有混合样本下估计方法的构造思想与非平衡面板数据下迭代极大似然估计方法相结合，有效处理部分平衡和部分不平衡的特殊非平衡样本的方差-协方差矩阵，将非平衡面板数据下迭代极大似然估计方法拓展到混合样本，并保证估计方法具有良好性能。

1 模型及样本设定

其中，i=1，…，N，t=1，…，T；yit为第t期第i个个体的观测值，xit为k×1维外生解释变量，β'=(β1，β2，…，βk)为待估参数，eit为随机误差项，设定为双因素误差：

其中，ui为不可观测的个体特殊效应，vt为时间效应，ωit为剩余的随机扰动项，ui、vt和ωit相互独立，且服从均值为0的同分布，同时：

对于所有的i、t、k和s，δ为克罗内克积，则有：

其中，σ2=σu2+σv2+σω2为总方差，ρ=σu2/σ2为个体效应方差比例，ω=σv2/σ2为时期效应方差比例[5]。

混合样本设定：先将被观测个体连续编号，由编号为1，2，…，N1,N1+1，N1+2，…，N1+N2的个体组成第一观测时期的样本；再将第一时期个体编号为N1+1，N1+2，…，N1+m( 0 ≤m≤N2)的个体由总体中编号为N1+N2+1,N1+N2+2,…,N1+N2+m的个体替代，其余部分保持不变，1，2，…，N1为普通面板数据观测个体，两个部分共同构成了第二观测时期的观测个体。此过程为对前一期从样本N1+1,N1+2,…,N1+N2中去掉m个被观测个体，而从被观测总体中引入m个新个体，进而形成轮换部分后一期的观测个体，普通面板数据观测个体保持不变，这样每一期的观测数目相同，观测T期，被观测不同个体总数为H=(T-1)m+N1+N2，观测个体总数为T(N1+N2)。

2 混合样本下扰动项方差-协方差矩阵

为了得到混合样本下的迭代极大似然估计，先需要得到T(N1+N2)个观测个体方差-协方差矩阵的解析表达，参照Arkadiusz 等（2020）[4]采用线性变换对非概率和概率样本整合的思想，本文引入样本设计矩阵实现普通面板数据和轮换面板数据的整合，得到混合样本下的方差-协方差矩阵。

由于T期观测个体总数为1，2，…，H，故将观测时期t的扰动项向量表示为：

取εit为N1+N2个个体中第i个个体的扰动项，则：

引入样本设计矩阵Dt，则εt可由et表示为：

其中：

其中，0N，n为N×n零矩阵，IN为N×N单位矩阵，Dt矩阵中( )i，j位置元素1表示总体中第j个观测个体是样本t期中的第i个观测个体。

通过式（6）和式（7）可得到：

其中，EH表示所有元素均为1 的矩阵。对于所有观测时期t，Dt D't=IN1+N2且Dt EH D't=EN1+N2，则：

其中：

取ε表示全部观测个体T(N1+N2)×1的扰动矩阵，记为：

则扰动项方差-协方差阵矩为：

3 参数的迭代极大似然估计

与ε类似，y可表示为T(N1+N2)×1 的向量，设定f(x;β)为f(xit;β)的矩阵表达式，假设随机扰动项服从正态分布，则y的对数似然函数可写成：

其中，ε表示y-f(x;β)；D由样本设计决定，如果ρ和ω已知，则矩阵Ω已知。这样，β、ρ、ω和σ可通过如下两步交互迭代求解得到：

步骤（1）：设定ρ和ω，将β视为极大似然估计的待估参数，可通过最小化Q=ε'Ω-1ε求得。

步骤（2）：通过步骤（1）得到β，将ρ、ω和σ视为待估参数，可通过最小化T(N1+N2)lnσ2+ln |Ω|+σ-2ε'Ω-1ε求得待估参数。

极大似然估计迭代算法开始需要设定ρ和ω的初始值，为方便起见，选择ρ=ω=0，即由步骤（1）计算得到的β为最小二乘估计。迭代算法的实现过程需要Ω-1和 |Ω|的解析表达式，在实际运行中，将涉及计算Ω的特征值，而这个过程过于复杂，因此本文考虑在实际应用中常被关注的一类特殊情形：N2=2m，m=kN1(k=1，2，…) ，即混合样本中轮换面板部分为二分之一轮换面板，且轮换面板数据的每期观测个体为普通面板数据的偶数倍（多轮换少面板情况），在实际应用中，当数据来源于真实微观数据且观测时期T较小时，估计结果受到的影响主要来源于观测个体效应扰动项，时期效应扰动项带来的影响较小。考虑到实际应用，本文将忽视时间效应扰动项，即设ω=0。

当N2=2m，m=kN1(k=1，2，…) 时，从式（7）可知：

将式（12）代入式（9）和式（10），可得：

且Ω1可分解为矩阵D和E，其中：

通过引理1,Ω-1可写成：

通过对混合样本进行样本设计，可将向量εt分解成εt=(εtA，εtB，εtC)，其中：

其中，εtA为普通面板数据中被观测个体在观测t(t=1，2，…，T)期的扰动项，εtB为轮换面板数据中t-1和t(t=2，…，T)期都被观测的个体在观测t期的扰动项，εtC为轮换面板数据中在t和t+1(t=1，…，T-1) 期都被观测的个体在观测t期的扰动项。

合并式（10）、式（13）和式（15），这样，迭代步骤（2）中二次型Q可表达成一种简化形式：

其中：

将式（14）和式（16）代入式（11），则对数极大似然函数可写成：

对上述对数极大似然函数关于σ2求偏导，得到如下条件估计量：

将σ̂2代入对数极大似然函数中得到中心对数极大似然函数：

进一步，关于ρ求偏导，可以得到对数似然方程：

式（18）不能得到参数ρ的显式解，但是可以得到迭代式：

其中：

其中：

给定初始值ρ(0)，反复利用式（19）进行迭代就可得到ρ的极大似然估计近似值ρ̂。

4 数值模拟

本文运用蒙特卡罗模拟方法研究普通面板数据和二分之一轮换面板数据混合样本下极大似然估计量的小样本性质，并与相同形式普通面板数据下极大似然估计量进行比较。将数据生成过程设定为如下形式[5]：yit=5+0.5xi2t+eit，其中，i=1，…，N；t=1，…，T。外生解释变量的生成过程为xit=0.3t+xi(t-1)+εit，xi0=100+250τit，τit相互独立且服从[- 0.5，0.5]上的均匀分布；随机扰动项的分解表达式为eit=ui+vt+ωit，其中ui、vt、ωit相互独立，且分别服从均值为0，方差为σu2、σv2、σω2的正态分布，其中σu2、σv2、σω2服从( 0 ，1.5) 上的均匀分布。

在模拟过程中选取以下9种不同的样本组合，选择样本 组 合N1=10 和T=3，5，10 ，N1=50 和T=3，5，10，N1=100 和T=3，5，10 ，对于每组样本组合，k=1，2，3,4。其中N2表示轮换面板数据每期观测个体数，T表示观测时期，N1表示普通面板数据每期观测个体数，n表示观测不同个体总数。记β̂表示本文提出的混合样本下迭代极大似然估计量，βˉ表示与混合样本形式相同的普通面板数据下极大似然估计量。

基于上述数据生成过程及随机样本，通过蒙特卡罗模拟可得混合样本下参数β的近似极大似然估计值β̂和普通面板数据下参数β的极大似然估计值βˉ。将以上过程重复1000次。计算出极大似然估计量的平均绝对偏差B=，及均方误差MSE=。具体结果见表1至下页表3。

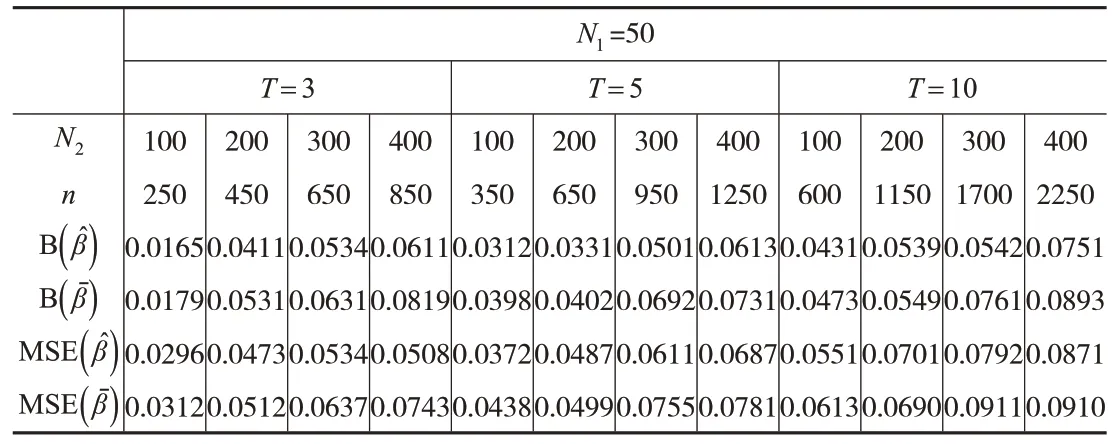
表2 β 迭代极大似然估计的平均偏差及均方误差( )N1=50

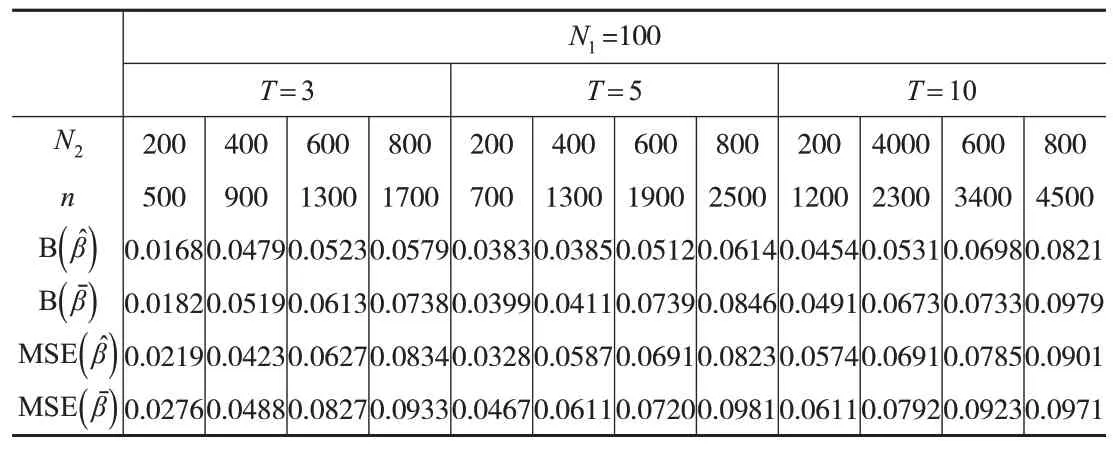
表3 β 迭代极大似然估计的平均偏差及均方误差( N1=100)

从表1至表3可以看到，总体上，当每期轮换样本占总样本的比例增加时，参数估计量的平均偏差和均方误差也随之增加。对于相同观测时期，参数估计量的平均偏差和均方误差随着样本容量的增大而增大。从模拟结果来看，与普通面板数据下极大似然估计量相比，本文提出的混合样本下迭代极大似然估计量在不同样本量、不同样本组合比例及不同观测时期下，整体上有较好的平均绝对偏差和均方误差，本文提出的方法优于面板数据下的极大似然估计方法。

5 结论

本文研究了普通面板数据与轮换面板数据混合样本下双因素误差面板回归模型的参数估计，将Arkadiusz 等（2020）[4]的混合样本整合思想与非平衡面板数据下迭代极大似然估计方法相结合，提出了混合样本下的迭代极大似然估计方法，得到了未知参数的迭代公式。蒙特卡罗模拟结果表明，混合样本下迭代极大似然估量的平均偏差和均方误差受轮换样本占总样本的比例及样本容量等因素的影响，比仅用普通面板数据所得到估计的平均绝对偏差和均方误差整体上都要小，估计效果较好。本文提出的混合样本下迭代极大似然估计方法优于普通面板数据下的极大似然估计方法，丰富了混合样本推断方法，为解决混合样本推断问题提供了新思路。