高压水射流在飞机发动机叶片清洗的应用
2023-10-15范晓宇
范晓宇, 纪 云
(1.中国航空发动机集团有限公司, 北京 100097; 2.燕山大学 机械工程学院, 河北 秦皇岛 066004)
引言
在航空工业中,发动机维护、维修和大修至关重要,以确保飞机的持续适航性和安全飞行操作。发动机在一定飞行时间或周期后都需要定期检查,特别是需要进行发动机清洗或在意外事件后进行发动机叶片维修。飞机维修故障是27.4%死亡率和6.8%飞机事故的主要原因,最常见的部件故障是发动机故障。由于飞机压缩机和发动机暴露在极端条件下, 特别是高温离心力、高压、高温、异物损坏及振动,因此,飞机发动机日常维护对飞机安全性非常重要。
飞机发动机叶片清洗作为飞机维护的重要部分,主要是为清除残留在叶片上的二硫化钼积层。通常,清洁方法分为物理、化学和生物清洁[1-3]。化学清洗,可以使用不同的化学品来降低或提高pH值,从而降低污染物质和膜之间的相互作用;生物清洗,是使用生物活性剂去除膜污垢。物理清洗广泛通过水力、机械和超声波工艺实现,以去除可逆污垢层[4]。发动机叶片常用超声波清洗方法[5],由于超声波清洗容易对飞机叶片造成侵蚀磨损,清洗过程中损伤叶片表面,且清洗不均造成的空化腐蚀也会影响飞机叶片的表面质量,因此现在研究人员聚焦于其他种类的飞机叶片清洗方法。
空气中的高速水射流广泛用于制造业中的切割和清洁操作[6-10]。水射流用于去除基材上的各种涂层或沉积物,也用于切割许多材料。虽然水射流切割涉及连续射流穿透固体材料,但水射流清洗涉及侵蚀过程,通过该过程从材料表面去除沉积物[11-12]。HASHISH等对射流切割过程进行了分析和实验研究,通过控制体积分析,以评估水动力,并研究间隔距离对清洗效果的影响,研究发现清洗水射流的速度范围通常为80~200 m/s。
高压水射流在空气中的剖分结构如图1所示[13]。这种射流可分为三个不同的区域:

图1 空气中高压水射流的剖分结构Fig.1 Sectional structure of high-pressure water jet in air
(1) 潜在核心区域:该区域靠近喷嘴出口。在这个区域,一次和二次不稳定性导致空气和水之间的质量和动量传递。空气夹带过程将连续的水分解成液滴。仍有一个楔形的潜在核心被混合层包围,其速度等于喷嘴出口速度。
(2) 核心区域:水与周围空气的持续相互作用导致水射流破碎成液滴,其尺寸随着距轴线径向距离的增加而减小。由于射流将动量传递到周围空气,其平均速度降低,因此水滴区扩散。最靠近喷射轴的区域称为水滴区,还有另一个区域,即将液滴区与周围空气分离的水雾区,该雾区的特点是水滴非常小,速度可忽略不计。
(3) 扩散液滴区域:该区域由射流完全分解成速度可忽略的非常小的液滴而产生。
本研究通过数值模拟,了解飞机发动机叶片水射流清洗的特性,这些射流通过质量和动量传递过程在周围大气中扩散,空气被夹带到射流中,整个过程有助于射流的扩散和随后的压力衰减。使用数值方法获得了叶片表面上速度及压力的大小和分布,根据数值结果,得出结论:增大水射流入口压力会增加清洗效率,但单次清洗面积及清洗增长率下降,增大入口压力意味着较大的水量消耗,会导致射流从清洁表面反弹并阻碍喷嘴流动,从而降低清洁效率。
1 高压水射流清洗模型
1.1 控制方程与求解方法
该问题的控制方程是湍流多相流的Navier-Stokes方程,为这个问题选择的多相模型是欧拉多相模型,采用具有标准壁函数的k-ε湍流模型来计算湍流。采用欧拉-拉格朗日液固两相流模型,粒子和液相之间采用双向耦合,粒子相采用Discrete Phase Model模型,用于计算液固两相流粒子-壁面冲蚀磨损。
多相流欧拉模型中w(水)相的连续性和动量方程分别为:
(1)
(2)
式中,εw—— 水相的体积分数
ρw—— 水相的密度
vw—— 水相的速度矢量
p—— 流体相压力
Sw-a—— 水相-气相相互作用体积力
1.2 侵蚀磨损模型
侵蚀是由于粒子对管道表面的反复冲击而发生的机械过程,重复的粒子撞击将导致陨石坑形成,陨石坑将随着粒子撞击而增长。脆性材料在水射流冲击下会产生横向和径向裂纹,这些裂纹会逐渐成长并最终形成块状裂纹,持续的水射流冲击将块状裂纹移除。另一方面,流动参数对侵蚀的影响更强,因为它决定了粒子浓度、粒子冲击角、冲击速度和作用对象表面的性质,即表面硬度和多相效应。
通过使用CFD,在理解固体粒子引起的侵蚀方面取得了进展。CFD允许对通过管道和弯管的流体流动和粒子轨迹进行精确建模。一旦计算出粒子碰撞表面的冲击速度和角度,就可以实现量化侵蚀率的经验关联[14]:
(3)

f(α) —— 粒子冲击角函数
C(dp) —— 粒子的粒径函数

C(dp)函数表示为分段线性、分段多项式或多项式函数,以便将其定义为墙边界条件的一部分,可通过其中一种方法来近似文献中的函数。
上面计算的侵蚀率以单位时间内冲蚀面积为单位,即质量通量,因此可以根据Fluent中定义的单位进行相应更改。C(dp)和f(α)函数必须以一致的单位指定,以建立具有相对粒子速度及其指数的无量纲群。侵蚀率为单位时间单位面积内去除掉的质量,可以定义自定义函数将侵蚀率除以壁面材料的密度,也可以将此划分包含在C(dp)和f(α)函数的单位中。
因不考虑入口质量流率对粒子冲蚀速率的影响,对式(3)进行无量纲处理:
(4)
使用CFD直接计算颗粒撞击角、撞击速度和质量流率。然而,冲击角函数、粒径函数和速度指数作为函数输入,如表1所示。
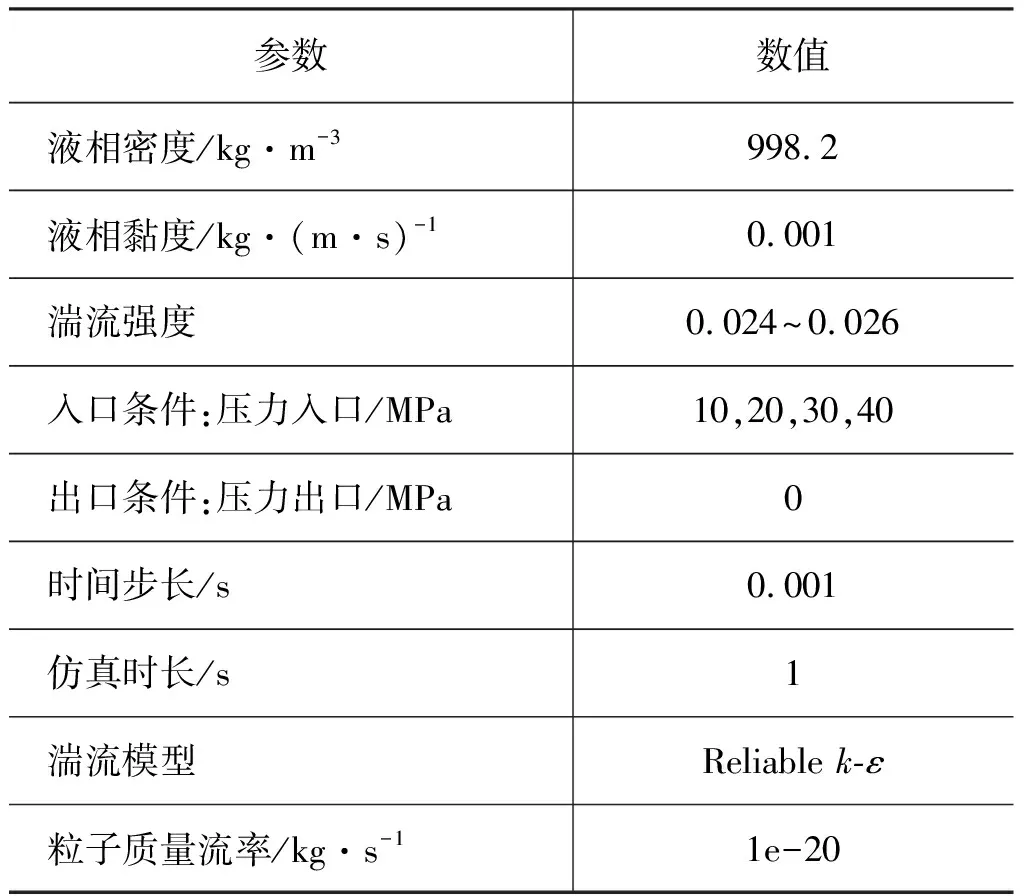
表1 参数表Tab.1 Parameter table
借助Hypermesh创建了计算域和结构化网格系统,如图2所示。区域的径向范围足够大,以确保压力出口边界条件和壁面边界条件能够准确应用,即不会对流场产生不利影响。使用了压力入口作为入口边界条件,压力出口作为出口边界条件。采用基于压力求解和时间精确的瞬态计算,为计算湍流,采用可实现的k-ε模型,近壁处理采用标准壁函数。采用有限体积法求解流体相控制方程,采用相位耦合简式求解压力-速度耦合精度,采用快速离散格式计算动量和湍流方程。在本研究中, 喷嘴出口速度是完全发展和湍流的,并且假设喷嘴是无摩擦的,因此喷嘴出口速度呈现顶帽特征。

图2 计算域与边界条件Fig.2 Calculation domain and boundary conditions
在所有计算中,压力-速度耦合都是使用相位耦合SIMPLE算法实现的,所有残差公差设置为0.001,时间步长为0.001 s,仿真计算时间为2 s。
2 仿真结果
2.1 网格无关性验证
对于一般的CFD数值计算,首先应该进行网格的无关性验证。对于网格尺寸来说,网格越小,数值计算精度越高,但计算成本随之提高,因此网格选取应在满足精度条件下尽量选择大尺寸网格。采用结构化网格划分流体域,网格大小分别为1.5, 2, 2.5, 3.0, 3.5 mm。
如图3显示了发动机叶片磨损量α与网格尺寸的关系,从图中可以看出,网格尺寸在3 mm时,仿真结果误差在5%以内,因此余下仿真案例所用网格尺寸为3 mm。

图3 网格无关性验证Fig.3 Grid independence verification
2.2 流场速度分布
根据边界条件及模型参数,进行了数值模拟,数值计算结果如图4、图5所示。
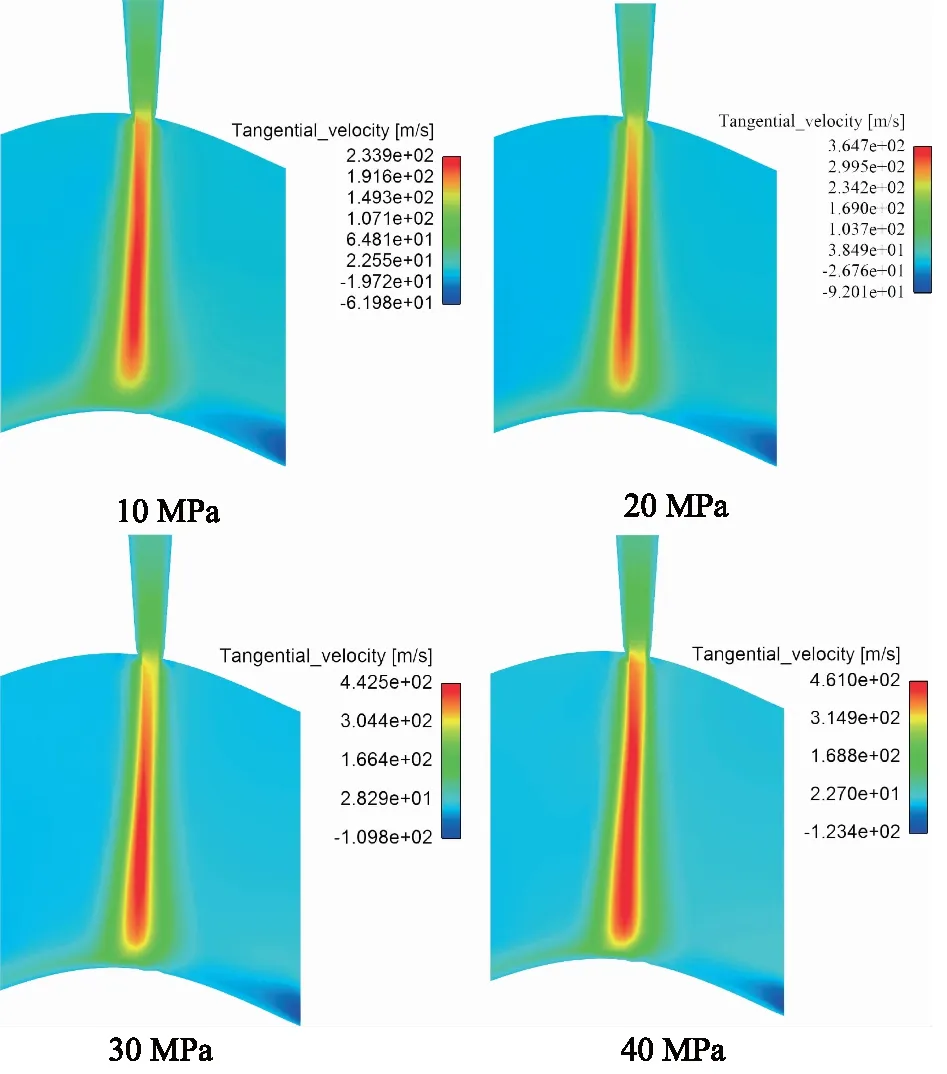
图4 不同入口压力下流场速度分布Fig.4 Velocity distribution of flow field under different pressures

图5 40 MPa压力下流场湍动能分布Fig.5 Distribution of turbulent kinetic energy of flow field under 40 MPa pressure
喷嘴入口压力已知,是大气压力,可以使用该参数以及入口压力数值来模拟喷嘴清洗叶片的流场特征。对于喷嘴几何形状,研究发现喷嘴内部的流动变成完全发展的湍流。在假设喷嘴入口处的湍流强度为10%且喷嘴无摩擦的情况下,喷嘴出口速度为顶帽形。图4及图5显示了四种不同入口压力下喷嘴中的速度和湍流强度分布。从图中可以看出,不同入口清洗压力下,随着入口压力的增大,水射流速度越高,清洗效率相应提高。但是,增大入口压力并不会增大单次清洗的面积。从图5可以看出,发动机叶片表面湍动能较大,多余的高压水在叶片表面形成水榭,进一步阻碍叶片的清洗效果。
图6显示了10 MPa水射流压力下液相的速度分布,从图中可以得出两个定性推断,即:

图6 10 MPa水流速度分布Fig.6 Velocity distribution of 10 MPa water
(1) 速度剖面是顶帽形的;
(2) 强剪切层集中在射流边界。
由于空气和水之间的尖锐密度界面,即使在(0.2~0.8)D时,速度分布仍然很高,且保持相当恒定状态。
2.3 叶片侵蚀
冲蚀工件作为实际工程运用中一项重要的表面处理技术,其不同工艺参数对冲蚀行为的具体作用规律及原因缺乏系统性研究[15],本节主要针对水射流入口压力进行模拟仿真,基于计算结果,对比分析不同入口压力对冲蚀深度总量的影响规律,如图7所示,并探究了其原因。从图7中可以看出,叶片侵蚀面积集中于较小面积内,该结果与流场速度结果吻合,这项工作将为飞机发动机叶片清洗理论提供参考。

图7 10 MPa压力叶片冲蚀效果Fig.7 Erosion of 10 MPa pressure
为研究入射压力对冲蚀结果的影响,取固体质量速率为1e-20 kg/s,分别在10, 20 , 30, 40 MPa四种入口压力下,获得叶片表面的冲蚀深度总量随入口压力变化的规律曲线,如图8所示。从图中可以看出,在四种不同入口压力下,冲蚀深度总量随着压力不断增大,整体的变化趋势基本一致。当入口压力增加到20 MPa 时,冲蚀增长率达到了最大值,后逐渐下降趋于稳定。结果表明,发动机叶片在实际清洗过程中,水射流入口压力应大于20 MPa,在过大入口压力下,其清洗效果相对于入口压力增加反而下降,清洗能耗率下降。

图8 不同入口压力侵蚀深度与增长率关系Fig.8 Relationship between erosion depth and growth rate of different inlet pressures
3 试验研究
喷嘴作为清洗的核心装备,其对于发动机叶片清洗效果及清洗效率重要。为此,对喷嘴入口直径d1、收缩段直径d2、靶距l3及收缩角θ开展正交试验设计,入口直径选取10, 12, 14, 16 mm,收缩段直径选取6, 7, 8, 9 mm,靶距选取40, 40, 60, 70 mm,收缩角选取45°,50°,55°,60°。取出口喷嘴清洗半径Rc作为衡量清洗效果的评价指标,如图9所示。

图9 喷嘴几何结构参数对清洗半径的影响Fig.9 Effect of nozzle geometric parameters on cleaning radius
从图9可以看出,入口直径及靶距对清洗半径呈正相关,收缩段直径及收缩角度对清洗半径负相关,收缩段直径及靶距对清洗半径呈线性变化,入口直径及收缩角度呈多次曲线关系。入口直径、收缩段直径、靶距及收缩角对高压水射流清洗半径的影响率分别为7.68%,30.61%,16.74%,12.99%,收缩段直径对水射流清洗半径影响最为显著。
表2显示每个因素的平均响应,表明该因素重要性排序,kj是每列中与“j”对应的测试数据的平均值,根据Rj值大小,可以判断各因素对试验指标的影响,Rj值越大,对指数的影响越大,影响因素越显著;Rj值越小,对指数的影响越小。根据极差分析可得因子排序为d2>l3>θ>d1,即在最大清洗半径情况下优先选取组合入口直径16 mm、收缩段直径6 mm、靶距90 mm、收缩角度50°,在该最优组合条件下,高压水射流喷嘴清洗半径最大,喷嘴清洗效率最高。
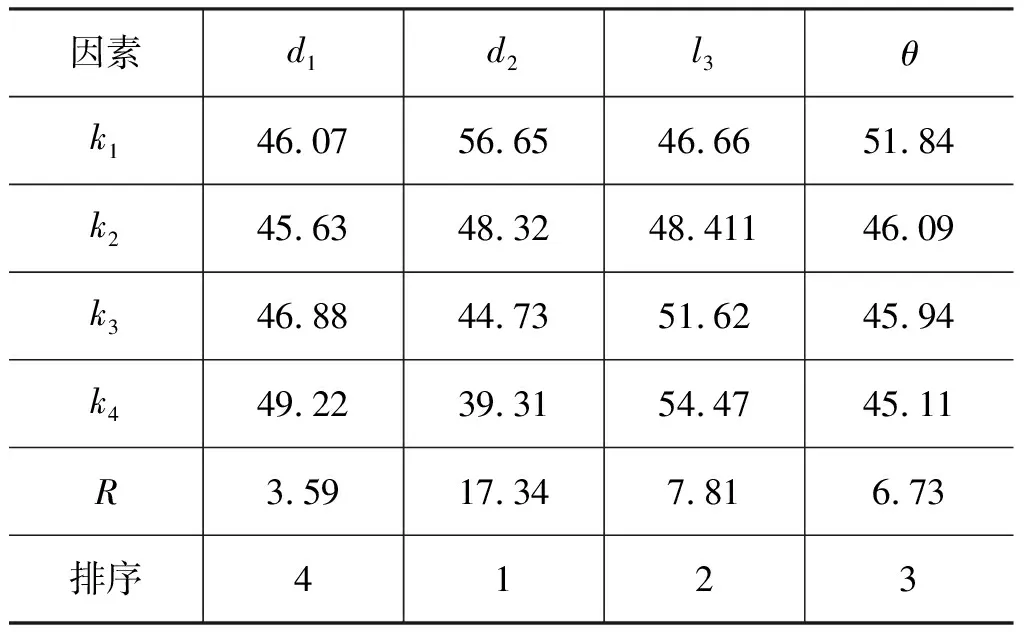
表2 喷嘴清洗半径的极差分析Tab.2 Range analysis of cleaning radius
4 结论
通过数值模拟,了解飞机发动机叶片水射流清洗的特性。使用数值方法研究发现增大水射流入口压力会增加清洗效率,但单次清洗面积及清洗增长率下降,增大入口压力意味着较大的水量消耗,会导致射流从清洁表面反弹并阻碍喷嘴流动,从而降低清洁效率。
模拟方法有助于预测工业清洁应用中使用的射流流动行为,因为这些应用集中在射流的近场区域。
正交试验表明,喷嘴收缩段直径对喷嘴清洗半径影响最显著,对靶距及收缩角度有显著影响。为提高喷嘴清洗效率,应适当缩小收缩段直径、适当扩大靶距。正交试验为喷嘴清洗效果最优参数选择提供理论依据及实践参考。
