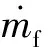火箭式旋转爆轰发动机推进性能的理论预测研究
2023-10-14魏良锴翁春生
魏良锴,肖 强,翁春生
(南京理工大学 瞬态物理国家重点实验室,江苏 南京 210094)
旋转爆轰发动机(rotating detonation engine,RDE)是一种利用持续旋转的爆轰波产生推力的发动机[1-2]。爆轰波是激波与化学反应强烈耦合的超声速燃烧波[3],具有极高的化学释热速率。由于爆轰波后温度、压力急剧增加,基于爆轰燃烧的动力装置无需压气机、涡轮等增压部件,可以极大减少发动机自重。旋转爆轰发动机因其较高的热循环效率在航空航天推进领域备受关注,是未来高性能空天动力的理想方案,具有广阔的应用前景。根据发动机是否自带氧化剂,RDE可分为火箭式和吸气式。目前针对RDE的实验研究主要以火箭式模态为主。
理论上火箭式RDE可以获得比恒压火箭发动机更优的推进性能。实验方面,科研人员通过改变燃烧室构型、喷管构型、推进剂组分等深入研究了火箭式RDE的推进性能,并不断优化发动机的结构设计,以期获得最佳的推进优势。KINDRACKI等[4]分别使用甲烷、乙烷、丙烷与氧气的混合气作为推进剂,测量了不同尺寸火箭式RDE的推力和比冲,根据实验结果,内径140 mm、外径150 mm的甲烷/氧气火箭式RDE在质量流量为0.21 kg/s时便可获得250~300 N的平均推力,单位面积推力高达1.1×105~1.3×105N/m2。俄罗斯FROLOV等[5]通过实验测得天然气/氧气火箭式RDE在32 atm的燃烧室平均压力下比冲为270 s,在相同的燃烧室平均压力下,RDE比冲约为当前广泛投入工程应用的RD170-A火箭发动机的两倍,直接证实了RDE的能量效率和推力性能优于传统发动机。BENNEWITZ等[6]使用甲烷/氧气推进剂针对带不同收敛喷管的火箭式RDE进行了一系列实验,系统测量了当量比在0.5~2.5以及质量流量在0.09~0.68 kg/s范围内的推进性能。实验结果表明,当量比为1.5、喷管面积收缩比为2.4、质量流量为0.444 kg/s时推进性能最好,该条件下比冲约为243 s。
虽然国内外学者针对RDE内爆轰波的点火起爆过程、传播特性以及发动机推进性能开展了大量的实验与数值仿真研究,但相应的RDE推进性能的理论预测研究却非常有限。分析其原因与发动机内非稳态的爆轰燃烧流场有关,流场的高时变特性给理论预测带来了极大挑战。与实验和多维数值计算相比,可靠的理论模型可以快速地为爆轰燃烧室的结构优化设计以及工作状态的调整提供指导,节约大量的资源。推进性能预测方面,STECHMANN等[7]提出了使用发动机出口热力学参数计算火箭式RDE推力的理论模型,并基于此模型分析了不同燃料、波前静压、波前静温、尾喷管构型对火箭式旋转爆轰发动机比冲的影响,计算结果与实验结果定性一致,误差约在20%~30%,该模型没有考虑斜激波的影响,认为火箭式RDE的燃烧室内部各处热力学参数仅有周向变化,而没有轴向变化,与旋转爆轰波的实际结构相差较大。SHEPHERD等[8]使用控制体表面动量平衡的方法建立火箭式RDE推进性能模型,将进气口截面压力拟合成指数函数,并引入BROWNE等[9]的Chapman-Jouguet(CJ)压力经验公式,以此求出了火箭式RDE的推力。SHEPHERD等的计算结果与实验误差在20%左右,但该模型假定燃烧室内气流始终为超音速,与实际燃烧室流场情况不符,并且该模型只适用于不带尾喷管的RDE,应用范围有限。孙健等[10]利用发动机各个壁面所受压力积分之和来计算发动机推力,并将结果与按照STECHMANN模型计算的结果对比,二者相差约为10%~20%,低质量流量下甚至可以达到30%,可以大幅抵消STECHMANN模型与实验的误差。该方法虽然可以获得与实验更接近的预测结果,但需要额外获得燃烧室出口的流场信息,给预测增加了一定的难度。
鉴于现有关于旋转爆轰发动机推进性能预测的理论研究均存在一些不足,本文旨在基于现有的理论模型,建立一个考虑燃烧室内爆轰波结构、更接近实际情况的火箭式RDE推进性能预测模型,并利用此模型分析推进剂组分、反应物当量比、推进剂温度、质量流量、喷管面积收缩比和扩张比等因素对火箭式RDE推进性能的影响,以期为火箭式RDE的燃烧室结构优化设计与工程应用提供快速的理论指导与参考。
1 推进性能计算方法
1.1 物理模型
火箭式RDE燃烧室的典型流场结构如图1所示。由图1(a)温度云图清晰可见燃烧室内的爆轰波、斜激波等结构以及预混气填充情况。文献[11-12]的研究表明RDE燃烧室内流场可以分为区域I和区域II两个热力学性质差异明显的区域,区域I存在爆轰波,区域II只有斜激波。区域I可以分为高压区和低压区。高压区内燃烧产物主要沿周向传播,低压区内工质主要沿轴向传播;区域Ⅱ内燃烧产物的传播方向是一个渐变的过程:靠近截面1高压区处传播速度有周向分量,而靠近截面2处可以认为传播速度只有轴向分量。
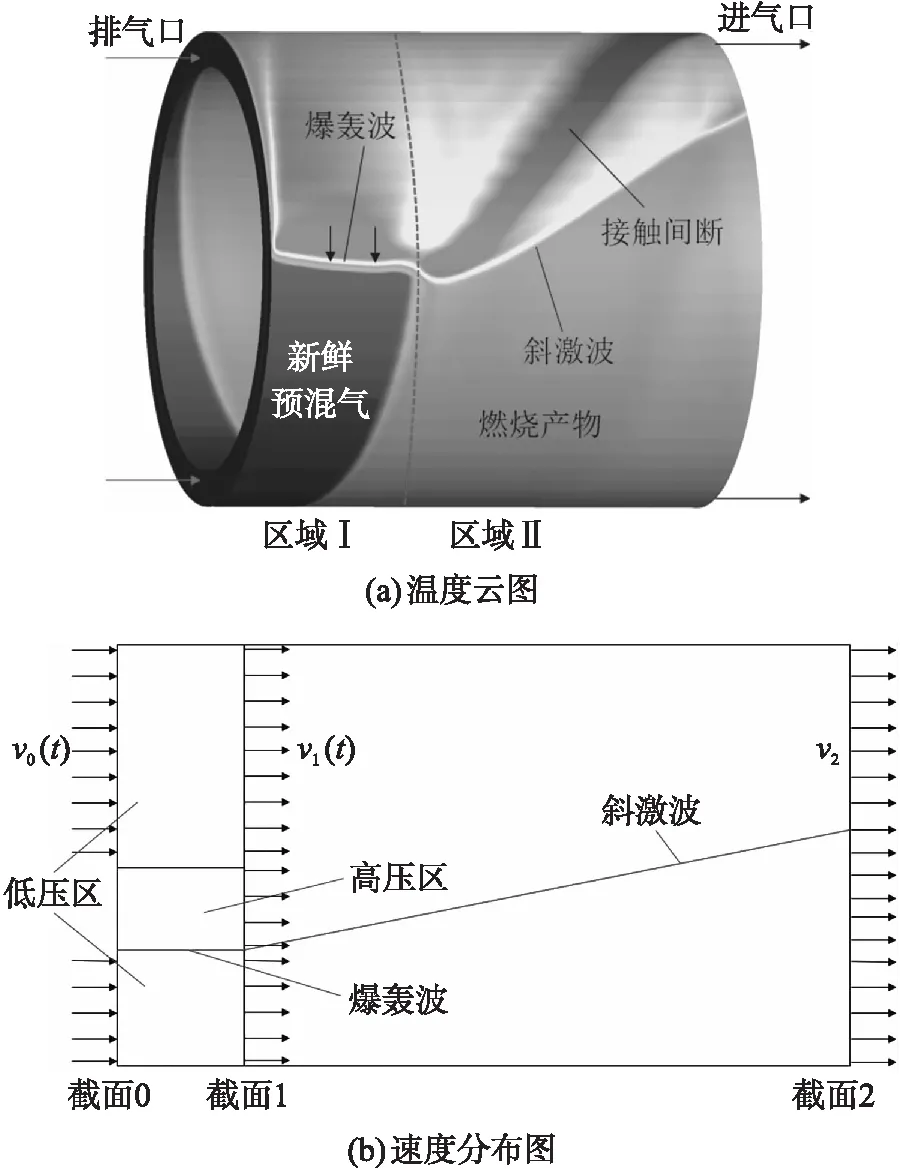
图1 火箭式RDE燃烧室温度云图和速度分布图Fig.1 Temperature distribution and velocity profile of rocket rotating detonation engine combustion chamber
文献[13]的研究表明,比起收敛尾喷管和扩张尾喷管,收敛扩张尾喷管对火箭式RDE的推力增益更大。鉴于此,本文仅对不加装尾喷管或者加装收敛扩张尾喷管的RDE开展研究。
为了简化分析模型,本文作出以下假设:
①推进剂及产物均为理想气体,且充分混合;
②燃料在区域Ⅰ完全燃烧且燃烧室内只存在一道持续传播的爆轰波;
③单个工况下,燃烧产物的比热比γ和分子量M在燃烧室内及尾喷管中各处都是恒定值;
④区域I的参数沿轴向均匀分布;
⑤根据文献[12],随着燃烧室轴向长度增加,燃烧室出口截面热力学参数趋于均匀。因此可以认为,对于本文所研究的长燃烧室,经过充分膨胀后,截面2各处燃烧产物的轴向速度、压力、温度、密度都均匀分布;
⑥尾喷管喉部马赫数始终为1。
1.2 计算方法
由于尾喷管喉部会出现壅塞现象,对于加装尾喷管的火箭式RDE和不加装尾喷管的火箭式RDE,推力和比冲的计算方法不同。下文对此分两节讨论。
1.2.1 不加装尾喷管的火箭式RDE
针对火箭式RDE,推力F由动量推力Fm和压差推力Fp两部分组成,即:
F=Fm+Fp
(1)
根据上文假设④,可以认为火箭式RDE出口处各热力学参数均匀分布,则Fm和Fp分别由下式计算得到:
(2)
Fp=(pe-pa)Ae
(3)
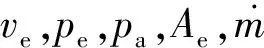
对应的火箭式RDE比冲为
(4)
式中:重力加速度g取9.806 65 m/s2。
根据文献[8],高压区内RDRE爆轰波波后任意点的压力可以近似表示为
(5)
式中:pi,pCJ,α,vCJ,h,t分别为波前推进剂静压、爆轰波峰值压力、由推进剂组分决定的压力衰减系数、爆轰波波速、爆轰波波头高度、爆轰波扫过该点后经过的时间(爆轰波衰减时间)。对于甲烷/氧气推进剂,α=0.65。
(6)
目前RDE主要采用多个收敛扩张(拉瓦尔式)喷嘴进气。为便于分析计算,近似认为所有喷嘴总出口截面积等于燃烧室横截面积。根据拉瓦尔喷嘴的气动特性,管内气流的流动状态受喷嘴出口背压(燃烧室中截面0处压力)的影响,具体可归纳为以下3种情形。
①进口拉瓦尔喷嘴喉部马赫数小于1时,预混气流在喷嘴内全程亚音速,此时截面0的压力p0(t)=p(t),截面0的马赫数为[14]
(7)
(8)
式中:γi,Ma1分别为预混气比热比和进口拉瓦尔喷嘴处于理想工作状态时的进口马赫数。
(9)
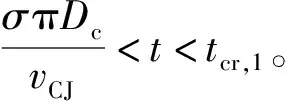
(10)
②进口拉瓦尔喷嘴喉部马赫数等于1,且喷嘴扩张段产生激波时,预混气仍以亚音速喷出。截面0的马赫数Ma0(t)通过下式求解[14]:
(11)
式中:Ae,in为进口拉瓦尔喷嘴的出口截面积,根据前文假设,Ae,in等于燃烧室截面积Ac。
满足该工作状态的截面0压力最大值为pcr,1,压力最小值为
(12)
式中:Ma2为进口拉瓦尔喷嘴处于理想工作状态时的出口马赫数。
(13)
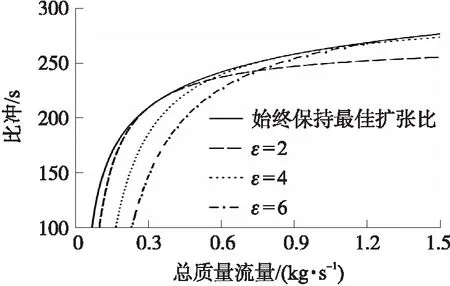
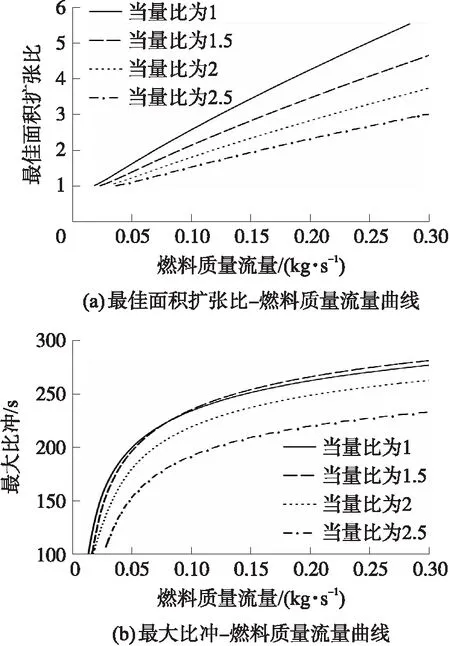
处于此工作状态下对应的爆轰波衰减时间t满足tcr,1 (14) ③进口拉瓦尔喷嘴喉部马赫数等于1。扩张段没有激波时,预混气以超音速喷出。此时截面0的压力p0(t)恒为pi,截面0的马赫数Ma0(t)恒为Ma2[14]。处于此工作状态下对应的爆轰波衰减时间t满足tcr,2 燃烧室截面0上密度、温度、速度参数可基于p0(t)与Ma0(t)通过等熵关系式求出。 (15) 式中:ρ0(x,y),ρ0(R,θ),ρ0(t)为截面0上密度;v0(x,y),v0(R,θ),v0(t)分别为速度关于直角坐标、极坐标、时间的函数;Rmax,Rmin分别为燃烧室外半径和燃烧室内半径。 根据质量守恒定律,经过时间δt,发生燃烧的预混气质量(δt时间内爆轰波扫过区域的气体质量)等于进入燃烧室的预混气质量,即: (16) 鉴于截面1上的压力p1(t)与截面0都保持一致的衰减规律,且不会受到进口拉瓦尔喷嘴的影响,因此p1(t)可用式(9)表示,而密度和温度通过燃烧产物的等熵关系式求出。 由于假设区域I的参数沿轴向均匀分布,因此可以认为截面1和截面0质量流量分布存在映射关系,则截面1的轴向速度随时间变化的函数为 (17) 截面2各参数由截面1各热力学参数计算得出。根据连续方程,有: (18) 因为截面1上气流方向在高压区和低压区不同,可以认为高压区有周向流动和轴向流动,低压区内由于稀疏波和斜激波共同作用,爆轰产物只有轴向流动。根据能量方程有: (19) 式中:γcp,Mcp,v1(t),T2分别为燃烧产物的比热比、燃烧产物的摩尔质量、高压区气流速度随时间的函数、截面2温度。高压区气流速度v1(t)为 (20) 波后气流横向速度vhp(t)根据文献[3]中的爆轰波两侧气流速度比公式求解。 在忽略斜激波阻力及燃烧室内摩擦力的情况下,轴向仅有压差引起的压力,对于截面1和截面2,由轴向的动量方程,有: (21) 根据式(18)~式(21),并结合截面2上的理想气体状态方程即可解出截面2上的密度ρ2、温度T2、压力p2、气流速度v2;p2,v2也即式(1)~式(3)中的出口压力和速度。 1.2.2 加装尾喷管的火箭式RDE 喷管喉部马赫数达到1时,在总压不变的情况下,无论喷管进口气流速度如何增加,通过喷管的质量流量不会增加,即喷管处于壅塞状态。由于RDE燃烧室气流是亚声速,喷管喉部的壅塞状态造成的扰动会一直沿上游逆流传播,从而减小波头高度h,使得进入燃烧室的质量流量减小,直至与壅塞状态的喉部质量流量相等[13]。 (22) (23) 出口压力pe和出口速度ve可以根据截面2的滞止压力和滞止温度结合喷管出口马赫数Mae计算。其中,Mae可根据喷管构型求解: (24) 式中:ε为喷管面积扩张比。 将由式(24)和式(26)求出的pe和ve代入式(1)~式(4),即可解出加装尾喷管的火箭式RDE的推力和比冲。 图2 计算流程图Fig.2 Flow chart of calculation 根据上述计算流程,基于文献[6]的实验条件开展相应的推进性能计算,然后将计算结果与实验结果进行比较分析。文献[6]采用的RDE燃烧室外径为76.2 mm,内径为66.04 mm,轴向长76.2 mm,RDE燃烧室出口分别采取无喷管以及面积收缩比和扩张比相同并分别为1.23,1.62,2.40的收缩-扩张喷管4种方案,其中面积收缩比为2.4的喷管在尾部加装中心锥。 本文模型计算的比冲与实验测得的比冲对比如图3所示。图3(a)、图3(b)分别为1.15和1.5当量比时4种尾喷管构型的比冲-质量流量曲线与实验结果对比图,不同曲线表示不同的尾喷管设计方案下的比冲理论值,离散点表示不同的尾喷管设计方案下的比冲实验值。图3(c)、图3(d)纵坐标表示本文计算出的比冲与实验值的误差(二者差值与实验值之比),不同曲线表示不同的尾喷管设计方案下的比冲误差曲线。 图3 本文计算的比冲与文献[6]中测得的比冲对比图和比冲误差图Fig.3 Comparison diagram and error diagram between calculation results and results measured in reference [6] 质量流量较大时,本文计算出的比冲约比实验比冲高10%,这是因为实验中由于侧向膨胀[15]、曲率效应[16]和边界层损失[17]等原因会造成爆轰波速度亏损,最终导致实验比冲低于理论比冲。值得注意的是,当质量流量很小时,计算出的比冲与实验值误差较大,均在20%以上,当量比为1.15、面积扩张比为1.23时,计算比冲甚至比实验值高50%。其原因是因为低质量流量下,排出气体的羽流会使环境压力降低,进而降低火箭式RDE的推力。但由于本文发展的计算模型并未考虑RDE出口复杂羽流场的影响,因此低质量流量下本文计算结果偏高。依照文献[10],低质量流量下考虑羽流计算出的比冲较不考虑羽流影响约低30%,与图3误差基本一致。 注意到,面积扩张比由1变化到1.62时,误差逐渐增大,但面积扩张比为2.4时误差小于面积扩张比为1.62时的误差,且面积比为2.4时,低质量流量误差和高质量流量误差相近。这是因为此构型在火箭式RDE尾部加装了中心锥,根据韩新培等[18]的研究,中心锥可以使排出气体进一步加速,从而提高推进性能。因此相比其余构型,此构型更接近本文的计算结果。根据文献[18],中心锥的存在可以有效削弱出口羽流的影响,因此面积扩张比为2.40的构型在低质量流量下误差和高质量流量一致。 鉴于文献[7-8]分别提出了RDE推进性能的计算模型,将本文模型与其进行比较,定量分析其差别。图4是使用本文方法和文献[7-8]中方法的比冲对比图。 图4 本文计算结果与文献中模型结果对比图Fig.4 Comparison diagram between specific impulse calculation results and previous model results 图4(a)和图4(c)分别为1.15和1.5燃料当量比下无喷管构型的比冲曲线对比图;图4(b)和图4(d)分别为1.15和1.5燃料当量比下带喷管构型的比冲曲线对比图,由于文献[8]无法计算带尾喷管的RDE,图4(b)、图4(d)只和文献[7]的计算结果进行比较。 可以看出,本文结果和文献[7-8]的计算结果趋势基本相同。对于无喷管构型,本文结果比文献[8]的结果约低13%,比文献[7]的计算结果约低6%;对于带喷管构型,本文结果比文献[7]的计算结果约低5%。 比文献[7-8]更接近实验结果的原因:①文献[8]中的模型假定燃烧室内气流始终为超音速,因此出口条件不会影响爆轰波传播,但事实上燃烧室内存在亚音速气流,按照此方法算出的比冲偏高;②文献[7]中的模型只考虑了爆轰波的影响,而没有考虑斜激波的影响,换言之,文献[7]中的模型认为图1(b)中截面2参数与截面1相同,而根据本文计算,截面2速度、压力均略小于截面1,因此按文献[7]中的模型计算结果高于实际情况。 尾喷管出口压力由尾喷管面积收缩比η=Ac/At和面积扩张比ε=Ae/At决定。由于η的增加会改变喷管喉部面积,进而影响通过喷管的最大质量流量,对RDE的推进性能产生消极影响,因此一般通过改变ε来调节推力和比冲。由于一般实验中η取值在1~2之间,本文取η为1.5来研究ε对比冲的影响。 除了质量流量很小的情况下,根据出口压力pe和环境压力pa的关系可将收敛-扩张喷管的工作状态分为3种:pe 基于上述理论分析,选用以当量比为1的甲烷/氧气为推进剂的火箭式RDE,分别加装面积扩张比自动调节以始终处于完全膨胀工作状态的可变喷管以及不同构型的固定喷管(面积扩张比分别为2,4,6),比较它们的比冲,如图5所示。 从图5可以看出,在燃烧室构型和进气条件相同的情况下,相比采用固定喷管的火箭式RDE,采用始终处于最佳膨胀状态的喷管的火箭式RDE比冲更大。 图5 分别加装可变喷管和固定喷管的RDE比冲曲线图Fig.5 Comparison of specific impulse of rocket RDE with variable nozzle and fixed nozzle 保证波前静温不变,基于BENNEWITZ实验尺寸,使用不同当量比的甲烷/氧气推进剂,算出最佳喷管面积扩张比-燃料质量流量曲线以及最大比冲-燃料质量流量曲线,如图6所示。 图6 不同当量比下最佳喷管面积扩张比以及最大比冲曲线Fig.6 Optimum area expansion ratio and maximum specific impulse curves with different equivalence ratios 图7为固定当量比下改变波前静温的最佳喷管面积扩张比-燃料质量流量曲线和最大比冲-燃料质量流量曲线。 图7 不同波头静温下最佳喷管面积扩张比和最大比冲曲线Fig.7 Optimum area expansion ratio and maximum specific impulse curves with different inlet temperature 图7(a)中纵坐标是在喷管喉部面积不变的情况下,出口气体处于完全膨胀状态的喷管面积扩张比;图7(b)中纵坐标是对应的比冲,不同曲线分别表示不同波前静温。 本文针对火箭式RDE建立了推进性能分析模型,基于此模型得到如下结论: ①本文模型对火箭式RDE的推进性能预测结果和实验较为接近,并且相较于文献[7-8]的推进性能模型更能模拟真实爆轰情况。但由于侧向膨胀、曲率效应和边界层损失等原因,本文预测结果比实验结果略高。低质量流量下(小于0.34 kg/s)本文算出的比冲与实验误差为20%~50%,高质量流量下(大于0.34 kg/s)本文算出的比冲与实验误差约为10%。 ②燃料当量比对比冲影响较大,不同推进剂组合获得最大比冲时的最佳当量比不同。对于甲烷/氧气的推进剂组合,最佳当量比是1.5。 ③爆轰波波前静温对火箭式RDE比冲的影响很小,可以忽略不计。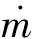
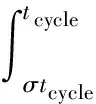
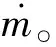
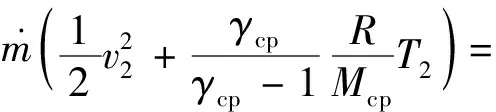
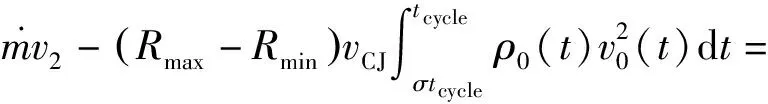
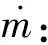
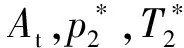
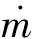
1.3 计算流程
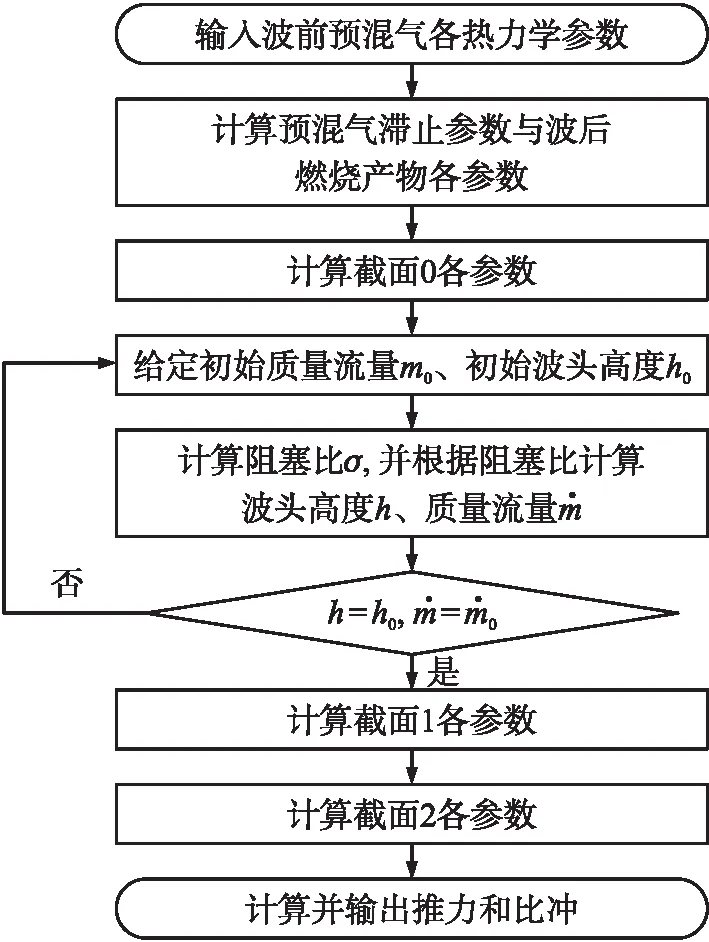
2 结果分析
2.1 与实验的对比
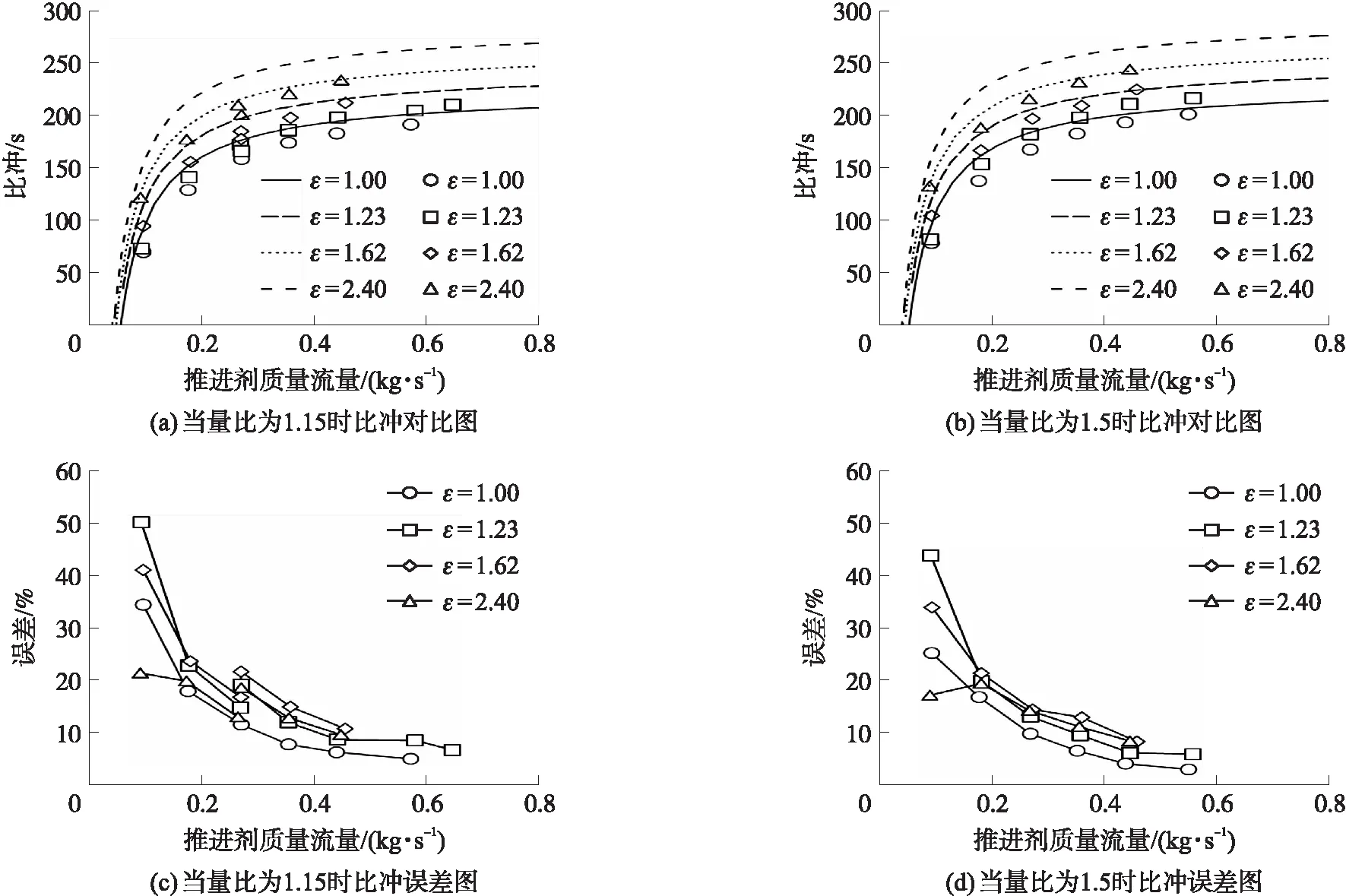
2.2 与其他模型的对比

2.3 最佳尾喷管设计方案

3 结论