分体式柔性矮桥墩抗震性能分析

孔凯歌

(广西交通设计集团有限公司,广西 南宁 530029)

0 引言

我国是一个桥梁大国,桥梁时常跨越复杂地形,应根据地形条件选择合适的桥梁及桥墩类型。其中,连续刚构桥由于墩梁固结,提高了桥梁的整体性,在地震作用下不易落梁以及减少了对支座的维护费用,得以大范围的推广应用[1]。连续刚构桥一般采用柔性高墩,不过,当受到线路标高或地形地貌限制时,连续刚构桥不可避免地需要采用矮墩。对于矮墩来说,其柔性较差,会增强桥梁刚度,这对连续刚构桥的抗震产生了不利影响,桥梁极有可能产生横向剪切破坏,危及人民的生命财产安全。因此,墩身刚度更小、抗震性能更好的分体式柔性矮桥墩成为研究方向之一,即将墩身分为若干肢,从而降低矮墩的刚度,提升抗震性能。

OpenSees有限元软件计算效率高,结果准确,建模的适用性强。因此,为了更好地研究分体式柔性矮桥墩的抗震性能,本文选择OpenSees有限元软件作为分析工具,对分体柔性墩的抗震性能进行分析,并与一般矮墩进行对比,研究成果可为分体式柔性矮墩的设计建设提供参考。

1 背景工程

本文以某矮墩连续刚构桥为背景工程[2-3],连续刚构桥的Midas Civil实体单元模型如图1所示。桥墩截面尺寸为8.0 m×3.0 m,桥墩高度仅为6.5 m。墩柱下设12 m×7.5 m矩形承台,承台高1.8 m,采用桩基础。桥墩保护层厚度为50 mm,沿桥墩长边方向布置有6层钢筋,每层布置94C28钢筋;短边方向布置有3层钢筋,每层布置26C28钢筋,主筋配筋率为3.3%。

本文以满足桥梁受力性能要求为依据,将上述矮桥墩设计为分体柔性矮墩,分体墩肢数分别为2、4和9,编号分别为P21、P22和P33,同时将整体墩编号为P11,各桥墩的参数如表1所示,实体模型如图2所示。

图1 矮墩连续刚构桥模型图

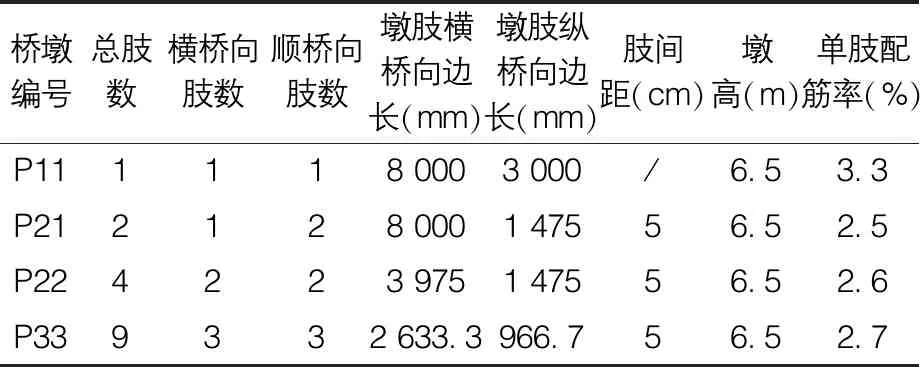
表1 分体柔性矮墩参数表

(a)P11

(b)P21

(c)P22

(d)P33

2 OpenSees简化模型的建立及加载

2.1 单元类型

本文采用OpenSees中的forceBeamColumn纤维单元模拟分体墩的墩肢,其模型示意图如图3所示[4]。forceBeamColumn纤维单元采用了分布塑性铰模型,该模型假设塑性铰出现在设定的积分截面处。相比于集中塑性铰模型,这更加符合桥墩的受力特点,在梁柱构件的模拟中得到了大量的应用。同时,forceBeamColumn纤维单元还采用了刚度法计算内力,相比于柔度法精度也更高。

本文将桥墩各肢分为5个单元,每个单元5个积分点。各墩肢的底部约束平动自由度和转动自由度,墩身不限制自由度。为了保证各肢顶部共同运动,采用equalDOF命令将各墩肢顶部自由度耦合。

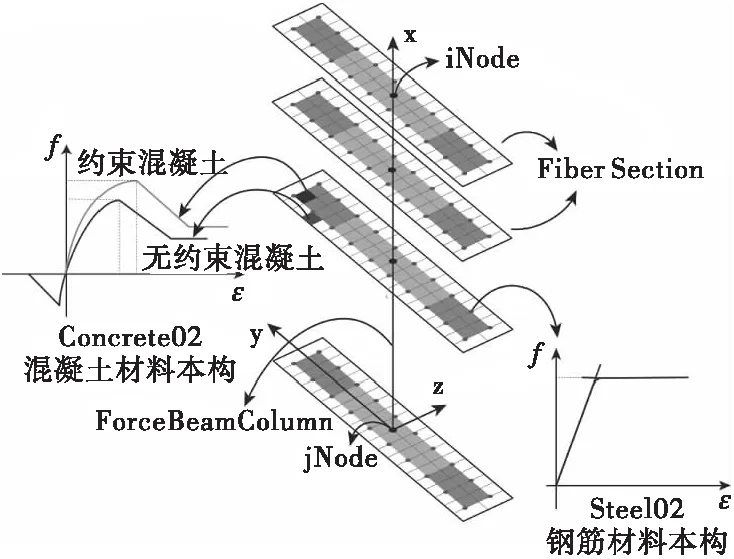
图3 forceBeamColumn纤维单元模型图

2.2 材料本构

各墩肢截面采用纤维截面模型,截面划分为钢筋和混凝土纤维并分别赋予本构模型[5]。由图3可知,本文采用Concrete02混凝土本构模型和Steel02钢筋本构模型分别混凝土和钢筋的应力-应变行为。

Concrete02混凝土本构模型采用了修正Kent-Park模型,采用混凝土强度提高系数考虑考虑箍筋的约束作用,同时还可考虑混凝土的受拉行为。Steel02钢筋本构模型是基于Menegotto和Pinto提出的简化双折线钢筋应力-应变曲线,能够考虑钢筋的屈服以及强化特性。

2.3 模型加载

本文采用位移控制的方式,在墩顶施加顺桥向的往复水平位移,加载等级为6.5 mm、13 mm,26 mm、39 mm、52 mm、65 mm、97.5 mm、130 mm、162.5 mm、195 mm和227.5 mm,每级循环两次,当墩身水平承载力下降到承载力峰值的85%或墩身不能继续加载时结束加载,加载制度如图4所示。

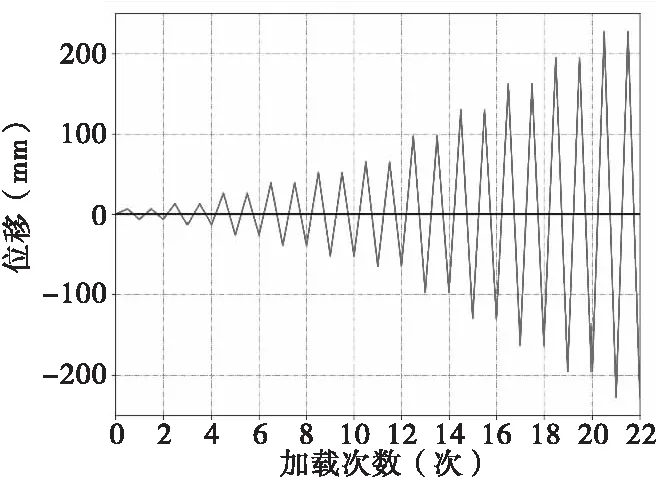
图4 加载制度曲线图

3 分肢对矮墩抗震性能的影响

3.1 滞回曲线和骨架曲线

图5给出了模型P11～P33的滞回曲线有限元计算结果。由图5可知,P11～P33滞回曲线均呈现出饱满的梭形,且均存在明显的下降段。

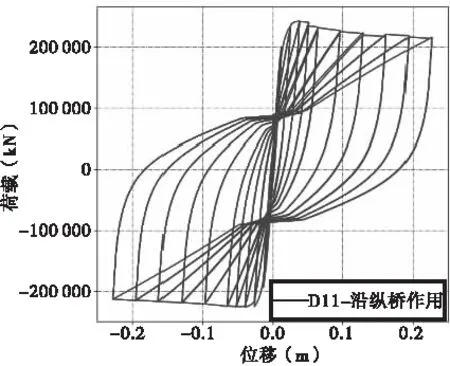
(a)模型P11

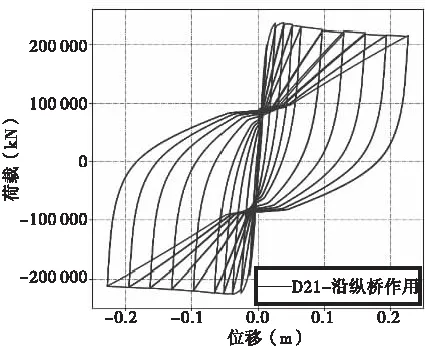
(b)模型P21

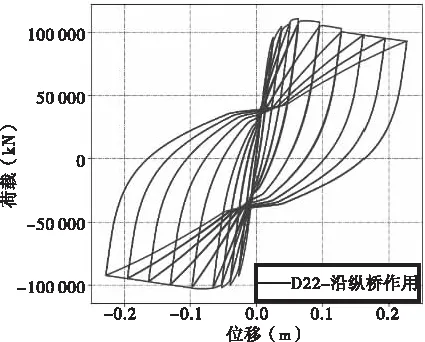
(c)模型P22

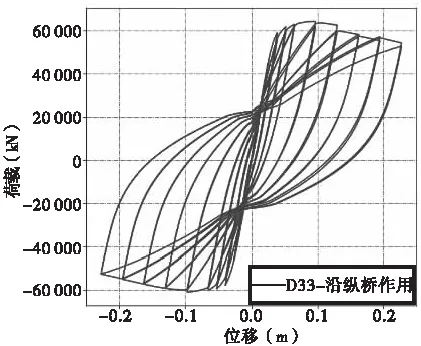
(d)模型P33

为了更好地对比不同分肢数对桥墩抗震性能的影响,提取出模型P11～P33滞回曲线的骨架曲线进行对比,如图6所示。由图6可知,将矮墩改为不同肢数的分体式柔性矮桥时,桥墩的骨架曲线存在明显的差异,提取各模型骨架曲线正向特征点数据列于表2。

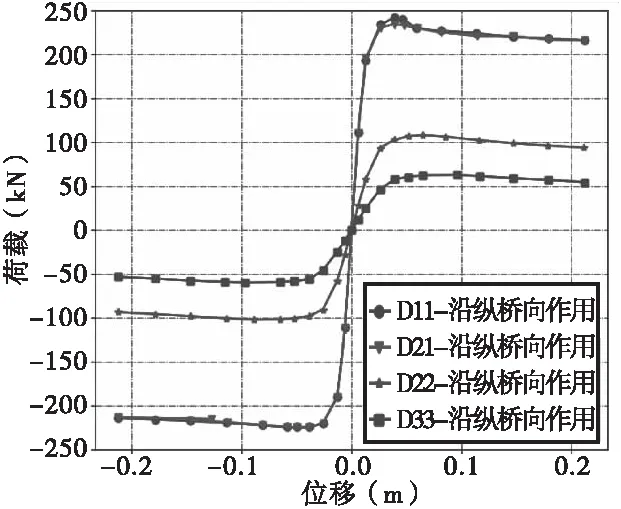
图6 骨架曲线对比曲线图

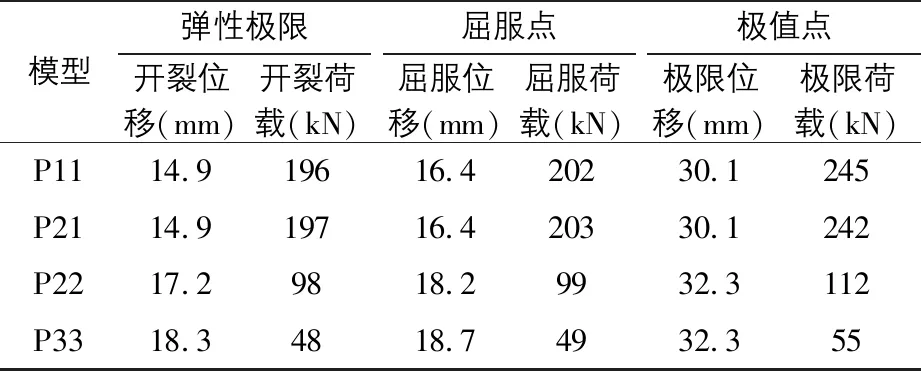
表2 骨架曲线特征点表

由图5和表2可知,模型P11和P21骨架曲线的弹性极限、屈服点和极值点的位移和荷载基本一致,但P21的承载力略有降低。表明当分肢数为2时,对桥墩的受力性能几乎没有影响。

由图6和表2还可知,模型P22和P33的骨架曲线与P11和P21存在明显的区别。如分体肢数为4和9时,其开裂位移分别为17.2 mm和18.3 mm,分别较P11增大了15.4%和22.8%;屈服位移分别为18.2 mm和18.7 mm,分别较P11增大了11.0%和14.0%;极限位移均为32.3 mm,较P11增大了7.3%。这表明,增加分体墩的分体肢数可以有效提高桥墩的弹性工作范围,延缓屈服,使其更晚达到极限荷载,较大地提高了柔性和抗震性能。

不过,由图6和表2可知,模型P22和P33的开裂荷载、屈服荷载和极限荷载均较P11和P21有较大幅度的下降。这并非表明分体墩无法满足桥梁的承载力要求,而是表明在进行分体墩的整体设计时,应考虑其承载力下降的因素,只需合理设计即可满足承载要求,同时具有较好的抗震性能。

3.2 刚度退化曲线

为进一步分析分体肢数对桥墩刚度的影响,图7给出了模型P11～P33的刚度退化曲线。

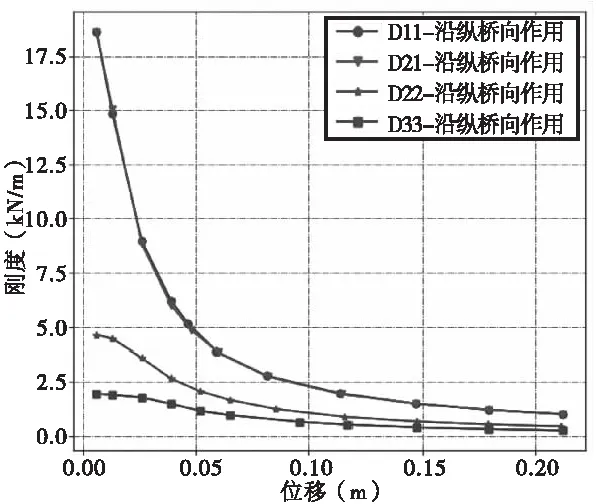
图7 刚度退化曲线对比曲线图

由图7可知,模型P11和模型P21的刚度退化曲线基本一致,这进一步表明分体肢数为2时,对桥墩的受力性能几乎没有影响。模型P22和P33的骨架曲线与P11和P21存在明显的区别。如模型P11～P33的初始刚度分别为18.1 kN/m、18.1 kN/m、4.8 kN/m和2.4 kN/m,P22和P33的初始刚度分别较P11和P21减小了73.4%和86.7%。这表明分体墩可以有效减小矮墩的刚度,提高其柔性,从而提高抗震性能。

由图7还可知,随着分体肢数的增加,其刚度退化速率也明显降低,有利于提高抗震性能。

4 结语

通过上述有限元分析,可以得到以下结论:

(1)采用OpenSees能够较好地进行桥墩的滞回性能分析。

(2)分体肢数为2时,分体墩的滞回性能与整体墩基本一致。随着分体肢数的增大,其开裂位移、屈服位移和极限位移均增大,表明分体墩可以增大桥墩的弹性工作范围,延缓屈服,使其更晚达到极限荷载,较大地提高柔性和抗震性能。

(3)分体肢数为2时,分体墩的刚度和刚度退化速率与整体墩基本一致。随着分体肢数的增大,分体墩的刚度和刚度退化速率均减小。表明分体墩可以有效提高桥墩的柔性,从而提高其抗震性能。