类方形蜂窝夹芯胞元尺寸的等效力学性能与优化

李响，黄欢，段宇，殷圣地

类方形蜂窝夹芯胞元尺寸的等效力学性能与优化

李响1,2，黄欢2，段宇2，殷圣地2

（1.三峡大学 石墨增材制造技术与装备湖北省工程研究中心，湖北 宜昌 443002； 2.三峡大学 机械与动力学院，湖北 宜昌 443002）

为了提升类方形蜂窝等效力学性能，在推导了其尺寸参数与等效力学性能的函数后，将尺寸参数作为设计变量、等效力学性能为优化目标，建立了类方形蜂窝夹芯胞元优化数学模型，采用了多目标遗传算法进行优化设计。给出胞元尺寸单参数响应及多尺寸协同作用的响应分析并从多目标优化代表性解中选取到最优解。优化结果得到：当夹芯胞元尺寸参数/取114.3899、/取0.9598时，等效密度增加59.52%，方向等效弹性模量减小了67.37%，但方向等效弹性模量增大了109.77%，等效剪切模量增加了421.94%，类方形蜂窝夹芯的等效力学性能显著提升。研究结果对类方形蜂窝夹层结构的优化设计提供一定的依据和参考。

类方形蜂窝；等效力学性能；优化设计；胞元尺寸

蜂窝夹层板作为典型的复合材料结构，因为其较高的比强度、比刚度和耐撞性能，被广泛的应用于汽车船舶、航空航天、工业建筑等领域。随着夹层结构在工程中的应用越来越多，人们对夹层结构的力学性能、稳定性和可靠性等指标提出更高的要求，传统的蜂窝结构已逐渐难以满足实际工程要求，需要开发出更多的新型蜂窝结构[1]。在国内外学者已提出了包括Kagome、内凹－反手性蜂窝等众多的蜂窝结构后[2-3]，基于仿生学的类蜂窝结构也被提出[4]，后来也设计出类方形蜂窝并对其力学性能进行了分析和研究[5-6]。但对这些夹芯结构胞元尺寸的取值目前还是参考了传统蜂窝结构的经验取值，为了得到性能更佳的结构，急需对蜂窝等效力学性能与优化设计进行研究。

目前，国内外的众多学者已对多种夹层结构进行了优化设计并取得了不错的成果。朱凌雪等[7]采用遗传算法，将梯度因子作为优化变量，比吸能为优化目标，对梯度点阵结构进行优化设计，在优化后，梯度结构的吸能性能提高了一倍。许琦等[8]以点阵夹层圆柱壳结构中的上中下板面的厚度、间距以及单胞内杆件的半径作为设计变量，以最小热传导系数、最大化一阶屈曲载荷、屈服强度为目标进行优化，给出了用于描述最小应力、最小质量、最小传热的最优解集。刘伟先等[9]从轻量化出发，以蜂窝夹层结构进气道为研究对象，研究了一种基于全局响应面算法的蜂窝夹层进气道优化技术。Yuan Chen等[10]研究了正常冲击和45°冲击对复合材料夹层结构能量吸收和破坏行为的动态影响并进行多目标优化，以提高正常和45°载荷下的能量吸收，优化后复合材料夹层结构的能量吸收能力可显著提高。Khalkhali等[11]采用多目标优化算法对波纹夹层结构进行优化设计，得到了在一定约束条件下的最佳解。Gholami等[12]采用粒子群算法对带有蜂窝的复合夹层结构进行优化，发现最佳的夹层板结构中的每个胞元横截面积最小而允许长度最大。虽然对于夹层结构力学性能和优化设计的研究较多，但对类方形蜂窝夹芯胞元尺寸力学性能和优化的研究还较为缺乏。

目前对类方形蜂窝研究的夹芯胞元尺寸参数取值均源于经验取值，并不能代表最优的力学性能，因此本文将研究类方形蜂窝结构胞元尺寸参数对等效力学性能的影响，并最终优化出拥有最佳力学性能的尺寸。本文所研究的类方形蜂窝夹芯胞元及其等效模型和主要尺寸参数如图1所示，其中类方形蜂窝夹芯等效模型单胞截面长度为、高度为、壁厚为。

图1 类方形蜂窝结构及其夹芯胞元尺寸参数

1 类方形蜂窝夹芯胞元尺寸优化设计

由以前的研究可知，类方形蜂窝为零泊松比蜂窝结构[13]，类方形蜂窝结构的等效力学参数主要包括方向等效弹性模量E、方向等效弹性模量E、等效剪切模量G和等效密度ρ，因此将以上的四个参数作为优化目标。

1.1 类方形蜂窝夹芯胞元尺寸优化设计变量及目标函数

研究发现，类方形蜂窝的等效力学参数与/、/的相关性比单独的更高，因此将/、/作为在优化类方形蜂窝夹芯胞元尺寸参数时的设计变量。

式中：为夹芯高度。

胞元质量为：

胞元等效实体的体积为：

等效实体的质量为：

依据推出的等效密度表达式及本课题组前期的研究工作，优化问题的目标函数为：

1.2 类方形蜂窝夹芯胞元优化数学模型

类方向蜂窝结构为薄壁结构，胞元壁厚对于边长、的值较小，因此综合考虑类方向蜂窝夹芯的力学性能指标，优化数学模型为：

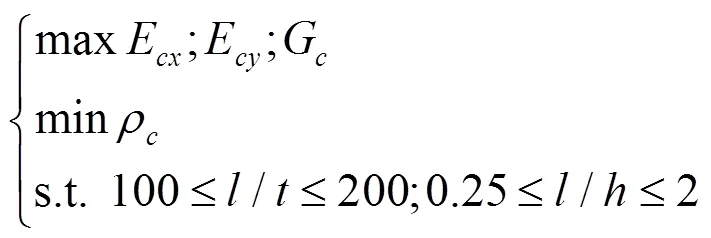
1.3 多目标遗传算法基本流程及算法设置

本文采用多目标遗传算法进行优化设计，为了得到准确度更高的优化解，将参数设定为最优前端个体系数0.5，种群大小100，最大进化代数200，停止代数200，其具体流程如图2所示。

图2 多目标遗传算法优化流程图

2 胞元尺寸的优化分析

将探究胞元的尺寸参数（/、/）对类方形蜂窝夹芯结构等效力学性能的影响，为方便研究，根据经验将尺寸的初始值设为＝0.02 mm、＝2.5 mm、＝5 mm，即设计变量的初始值为/＝＝125、/＝＝0.5。

2.1 胞元尺寸单参数响应分析

当/和/分别取初始值时，/和/对类方形蜂窝夹芯方向的等效弹性模量E的影响如图3所示。由图3可知，随着/的增大，方向的等效弹性模量减小，且增长率随着/的增大有一定的减小，但基本上近似于线性。而方向的等效弹性模量与/基本上呈线性相关。

图3 l/t和l/h分别对Ecx的影响

图4表示的是/和/对类方形蜂窝夹芯结构方向的等效弹性模量E的影响。从图4中可以看出方向的等效弹性模量都是随着/和/的增大而减小，且下降率也是随着/和/的增大而减小，变化范围也基本相同，但下降率随着/变化的趋势更为平缓。

/和/对类方形蜂窝夹芯结构等效剪切模量G的影响如图5所示。由图5可知等效剪切模量与/基本上呈正线性相关。等效剪切模量随着/的增大而减小，且下降率也随着/的增大逐渐减小。

图6显示的是/和/对类方形蜂窝夹芯结构等效密度ρ的影响。从图6可以看出等效密度与/呈正线性相关，而随着/的增大，等效密度减小，且下降率也随着/的增大而均匀减小。

图4 l/t和l/h分别对Ecy的影响

图5 l/t和l/h分别对Gc的影响

2.2 胞元尺寸协同响应分析

/和/协同作用时对类方形蜂窝夹芯结构y方向的等效弹性模量的影响如图8所示。由图8可知，/和/协同作用时，/和/对方向的等效弹性模量的影响趋势基本保持一致，都是随着/或/的减小，方向的等效弹性模量迅速增大。而当/（/）较大时，/（/）对方向的等效弹性模量几乎无影响；当/（/）较小时，方向的等效弹性模量随着/（/）的增大而迅速减小。

图6 l/t和l/h分别对ρc的影响

图7 l/t和l/h对Ecx的响应面

图8 l/t和l/h对Ecy的响应面

图9表示的是/和/协同作用时对类方形蜂窝夹芯等效剪切模量的影响。从图9中可以看出，/和/对等效剪切模量的影响效果基本相反。当/较小时，等效剪切模量几乎不随/变化；但当/较小时，等效剪切模量随着/的增大而迅速增大，且增长率基本保持不变。当/较大时，等效剪切模量随着/的增大而减小，且下降率也逐渐减小；但当/较大时，/的变化基本不改变等效剪切模量的大小。

图10为/和/协同作用时对类方形蜂窝夹芯结构等效密度的响应面。由图10可知，当/较小时，等效密度对/的敏感度较低，但随着/的增大等效密度对/的敏感度逐渐增强。而不论/取何值，等效密度对/的敏感度都较强，都是随着/的增大而基本呈线性下降，且随着的/增大，等效密度对/的敏感度也随之下降。

图9 l/t和l/h对Gc的响应面

图10 l/t和l/h对ρc的响应面

2.3 优化结果分析

由上述分析可得，在增大/时，虽然类方形蜂窝夹芯方向的等效弹性模量略有减小，但方向的等效弹性模量及等效剪切模量会明显增大，抗承载和形变能力变强，不过等效密度却会大幅上升，使得结构重量过重；在增大/时，虽等效密度有一定减小，但方向和方向的等效弹性模量及等效剪切模量也会随之降低。综上所述，该优化目标之间存在相互冲突，无法使得优化结果同时到达最优，因此需要根据实际情况来选取最优解。

基于上述多目标遗传算法的设置，得到基于目标函数和优化数学模型对应的Pareto解集，从Pareto解集中选取几组多目标优化的代表性解，分别用于描述类方形蜂窝夹芯结构的最大方向和方向等效弹性模量、最大等效剪切模量和最小等效密度，如表1所示。在拥有最大方向等效弹性模量时夹芯结构方向等效弹性模量较大，同时等效密度也较大，夹芯结构重量增加；在拥有最大方向等效弹性模量时会减小方向等效弹性量及剪切模量，夹芯结构抗剪能力下降；在拥有最大剪切模量时方向和方向等效弹性模量会减小，同时会增大等效密度，夹芯结构重量增加；而具有最小等效密度时夹芯结构重量最轻，但其余三个参数均较小，导致力学性能变差。

综上所述，夹芯结构在具有单一目标最优时，会导致其它目标性能变差，此时的夹芯结构并不是最优的。因此还需要在得到的Pareto解集中选取能满足四个目标函数的相对最优值，并将其与优化模型的初始值进行比较。因此经选取得到最终优化值的相关数据如表2所示。由表2可知，当/＝114.3899、/＝0.9598时，夹芯结构方向的等效弹性模量增加了109.77%，方向的等效弹性模量减小了67.37%，等效剪切模量增加了421.94%，但等效密度也增加了59.52%，使夹芯结构整体重量上升。总体而言，在类方形蜂窝夹芯结构的重量略有上升的前提下，其力学性能得到了优化，承载变形能力有了大幅提高。

表2 类方形蜂窝夹芯优化模型初始解和优化值

3 结论

将响应面法与多目标遗传算法相结合，以类方形蜂窝夹芯结构的尺寸参数/和/作为变量，对其方向等效弹性模量E、方向等效弹性模量E、等效剪切模量G和等效密度ρ进行优化设计，得到如下结论：

（1）在/取值确定时，方向和方向等效弹性模量、等效剪切模量和等效密度均随着/的增大而减小；在/取值确定时，方向等效弹性模量、等效剪切模量和等效密度均与/呈线性相关，但方向等效弹性模量却会随/的增大而减小。

（2）在/取较小值、/取较大值时，方向等效弹性模量、等效剪切模量和等效密度都能取到较大值；而方向等效弹性模量只在/和/均取较小值时才能取到较大值。

（3）当用多目标遗传算法对类方形蜂窝夹芯胞元尺寸进行优化设计时，尺寸参数/取114.3899、/取0.9598时，使其在等效密度增加59.52%和方向等效弹性模量减小67.37%的情况下，方向等效弹性模量增大了109.77%，等效剪切模量增加了421.94%，显著提高了其力学性能。

[1]李响，李锐，徐兴兴，等. 类蜂窝夹芯结构等效力学性能优化设计[J]. 燕山大学学报，2021，45（5）：402-408.

[2]Park J S，Joo J H，Lee B C，et al. Mechanical behaviour of tube-woven Kagome truss cores under compression[J]. International journal of mechanical sciences，2011，53（1）：65-73.

[3]魏路路，余强，赵轩，等. 内凹-反手性蜂窝结构的面内动态压溃性能研究[J]. 振动与冲击，2021，40（4）：261-269.

[4]李响，童冠，周幼辉. 超轻多孔“类蜂窝”夹层结构材料设计方法研究综述[J]. 河北科技大学学报，2015，36（1）：16-22.

[5]李响，周幼辉，童冠，等. 超轻多孔类蜂窝夹心结构创新构型及其力学性能[J]. 西安交通大学学报，2014，48（9）：88-94.

[6]童冠，李响，梅月媛，等. 类方形蜂窝夹芯结构力学性能研究[J]. 河北科技大学学报，2017，38（6）：522-529.

[7]朱凌雪，王同银，朱晓磊. 基于梯度化因子功能梯度点阵夹层结构优化设计[J]. 振动与冲击，2018，37（23）：98-103，110.

[8]许琦，阎军，蒋存存，等. 航天器点阵夹层圆柱壳构型多学科优化设计[J]. 载人航天，2020，26（2）：152-158.

[9]刘伟先，穆雪峰，曾果. 复合材料蜂窝夹层进气道结构优化设计方法[J]. 南京航空航天大学学报，2018，50（1）：86-90.

[10]Chen Y，Fu K，Hou S，et al. Multi-objective optimization for designing a composite sandwich structure under normal and 45° impact loadings[J]. Composites Part B: Engineering，2018（142）：159-170.

[11]Khalkhali A，Narimanzadeh N，Khakshournia S，et al. Optimal design of sandwich panels using multi-objective genetic algorithm and finite element method[J]. International Journal of Engineering，2014，27（3）：395-402.

[12]Gholami M，Alashti R A，Fathi A. Optimal design of a honeycomb core composite sandwich panel using evolutionary optimization algorithms[J]. Composite Structures，2016（139）：254-262.

[13]李响，王阳，杨祉豪，等. 新型类方形蜂窝夹芯结构泊松比研究[J]. 三峡大学学报（自然科学版），2019，41（3）：91-96.

[14]童冠，李响，梅月媛，等. 类方形蜂窝夹芯结构力学性能研究[J]. 河北科技大学学报，2017，38（6）：522-529.

Equivalent Mechanical Properties and Optimization of Quasi-Square Honeycomb Sandwich Cell Size

LI Xiang1,2，HUANG Huan2，DUAN Yu2，YIN Shengdi2

( 1.Hubei Engineering Research Center for Graphite Additive Manufacturing Technology and Equipment, China Three Gorges University, Yichang 443002, China; 2.College of Mechanical and Power Engineering, China Three Gorges University, Yichang 443002, China)

In order to improve the equivalent mechanical performances of quasi-square honeycombs, a mathematical model of cell optimization was established and a multi-objective genetic algorithm was used for the optimization design. With deduction of the function of dimension parameters and equivalent mechanical properties, the size parameters were taken as the design variables and the equivalent mechanical properties were taken as the optimization objectives, The optimized results show that when the/is 114.3899 and the/is 0.9598, the equivalent density rose by 59.52%, the-direction equivalent elastic modulus decreased by 67.37%. In contrast, the equivalent elastic modulus in-direction rose by 109.77% and the equivalent shear modulus rose by 421.94%. The equivalent mechanical performances of quasi-square honeycomb structure are significantly improved. The research results provide some basis and reference for the optimal design of honeycomb sandwich structures.

quasi-square honeycomb；equivalent mechanical performance；optimized design；cell size

O342

A

10.3969/j.issn.1006-0316.2023.09.001

1006-0316 (2023) 09-0001-07

2022-12-26

国家自然科学基金（51975325、51305232）；三峡大学石墨增材制造技术与装备湖北省工程研究中心开放基金（HRCGAM202108）

李响（1979－），男，湖北黄梅人，博士，副教授、硕士生导师，主要研究方向为轻量化技术、结构优化设计、数值模拟技术、结构强度与可靠性等，E-mail：lixiangcfy@ctgu.edu.cn。