基于广域多时间尺度的CVT 误差状态预测方法
2023-10-14成跃宇CHENGYueyu成国锋CHENGGuofeng
成跃宇 CHENG Yue-yu;成国锋 CHENG Guo-feng
(国网扬州供电公司,扬州 225009)
0 引言
习近平总书记指出,世界经济数字化转型是大势所趋。以数字化、网络化、智能化为特征的新一代信息技术日益创新突破,正在推动全社会进入数字化时代。当前,我国各类计量器具的监管和服务都逐步向信息化、智能化迈进,为此国务院出台《计量发展规划(2021-2035 年)》等文件,要求探索并推动计量法规数字化和管理创新化,“大力加强计量科技创新,加大基础、前沿和应用领域计量薄弱环节技术研究,推动计量产学研协同创新。探索建立新型计量监管模式和思路,推动计量制度改革,提升计量管理能力和水平。”
电容式电压互感器(Capacitor Voltage Transformer,CVT)是一种用于测量高电压系统中电压的传感器,其计量性能的可靠与稳定性直接影响电力系统保护、测控和计量的可靠性,CVT 超差故障直接导致测量失准,严重超差还可能引起继电保护装置误动作,后果严重。为此,国家出台《JJG 1189.4-2022 测量用互感器第4 部分:电力电压互感器》等检定规程,要求对CVT 开展停电校验,但传统的离线检定存在“检测不及时、停电时间长、检测成本高”等问题,亟需推动CVT 从按“周期检测”向按“状态评估”的转变。
对于CVT 误差状态预测的研究,目前主要有以下几个方向和方法:①统计模型,利用历史数据和统计分析方法,建立CVT 误差与一些关键参数(如温度、湿度、频率等)之间的关系模型。通过监测这些参数的变化,预测CVT的误差状态。常见的统计模型包括回归模型、时间序列模型等。②机器学习方法:使用机器学习算法(如支持向量机、神经网络、决策树等)来构建CVT 误差状态的预测模型。这些模型可以根据CVT 的历史数据和其他相关数据,学习CVT 误差与输入参数之间的潜在关系,并进行预测。③物理模型:基于CVT 的物理特性和工作原理,建立数学模型来描述CVT 的误差特性。这些模型可以考虑CVT 的结构、电场分布、电容器性能等因素,从而预测CVT 的误差状态和变化。
但是现有的预测方法只考虑单一粒度构建时序模型,存在数据维度单一、预测精度低的问题,为此,本文提出了基于广域多时间尺度的CVT 误差状态预测方法,从输入特征构建和预测模型优化两个角度对广域CVT 误差状态进行深入挖掘评估:在输入特征构建方面,深入挖掘CVT的二次输出数据的时序规律,采用STL 算法(Seasonal-Trend decomposition procedure based on Loess,基于局部加权回归的周期趋势分解)分解出趋势项、周期项和余项,构建了多元时间特征,解决了数据维度单一的问题;在预测模型优化方面,设计多层Transformer 结构,采用patch 尺寸来进行粒度控制,实现了任意粒度时间序列信息的建模,解决了可靠性差、预测精度低的问题。
1 CVT 误差特性
CVT 的误差特性通常可以分为2 个部分:比值差和相位差,具体定义如下:
其中,ε 表示CVT 的比值差,U1表示CVT 的一次电压,U2表示CVT 的二次电压,kr表示CVT 的额定变比,ρ表示CVT 的相位差,φ1表示CVT 的一次电压的初相位,φ2表示CVT 二次电压的初相位。CVT 的误差特性限值如表1 所示。
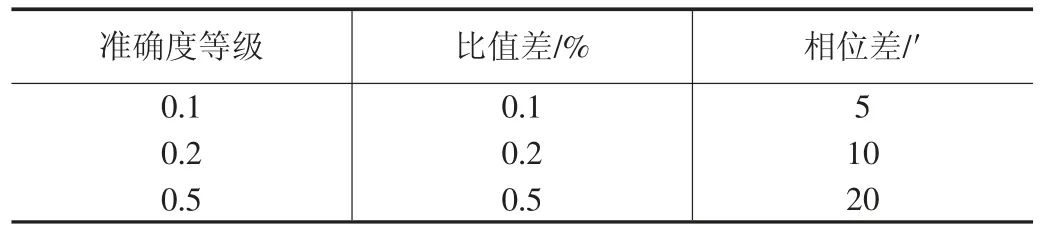
表1 CVT 基本误差限值
当CVT 的误差在基本误差限值内,CVT 属于正常状态;反之,超过基本误差限值则处于异常状态。
2 CVT 误差状态预测方法
2.1 总体技术路线
本文所提的基于广域多时间尺度的CVT 误差状态预测方法的总体技术路线如图1 所示,具体步骤如下:
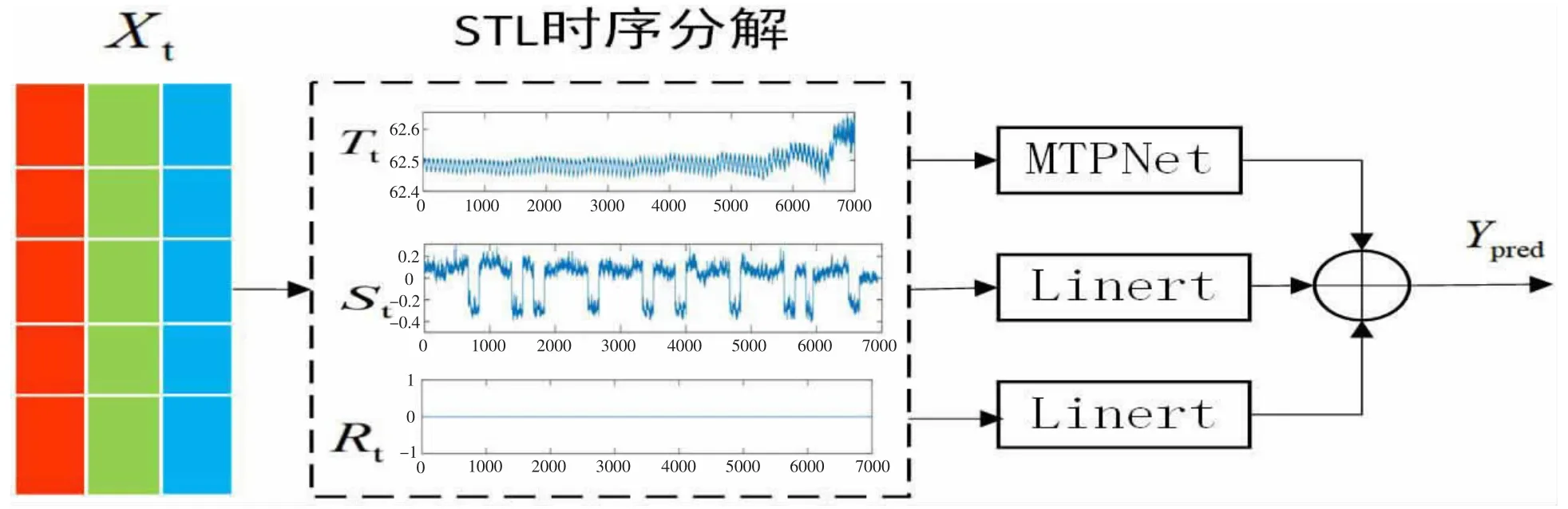
图1 总体技术路线
①数据采集:使用准确度等级为0.05 级的电压互感器在线采集装置从变电站中控室计量屏柜中采集正常CVT 二次输出数据;
②提取特征:分析广域CVT 二次输出数据的时序规律,利用STL(Seasonal-Trend decomposition procedure based on Loess,基于局部加权回归的周期趋势分解)分解出趋势项、周期项和余项,构建评估特征集;
③构建误差预测模型:采用线性模型建模趋势分量和余项,采用MTPNet(Multi-scale Transformer Pyramid Networks,多时间尺度变化的金字塔网络)模型建模周期项,然后将三个预测模型进行融合,得到CVT 误差状态预测模型;
④预测误差状态:将待测CVT 的二次输出数据经处理后输入至CVT 误差状态预测模型,实现CVT 运行误差状态的预测(正常状态、告警状态、异常状态)。
2.2 基于STL 的CVT 二次侧数据的分解
CVT 的二次侧数据Xt可被STL 分解为:
其中,Tt、St、Rt分别表示周期项、趋势项、余项。
STL 的具体分解过程可以分为2 步:即内循环和外循环。在内循环迭代时,主要是利用平滑期更新St和Tt,去除各分量的异常扰动;外循环迭代时,主要拥有计算Rt。第i+1 次迭代的过程如下:
①对CVT 的二次侧数据Xt进行去趋势项处理:
其中,Xt(detrend)表示去趋势项后的结果;Tt(i)表示趋势分量第i 次迭代结果。
②子序列平滑。对每个子序列进行局部加权回归(Lowess)平滑处理,前后各闫拓1 个时间点,组合得到新的子序列。
③采用低通滤波计算新实践序列的趋势项分量,去除周期性差异,然后由时间序列的可加性计算新时间序列的季节性分量,即:
④去除子序列中的季节分量,得到原始序列的季节分量和趋势分量,即:
2.3 CVT 误差状态预测算法模型的构建
本文设计的CVT 误差状态预测算法模型算法框架如图2 所示。
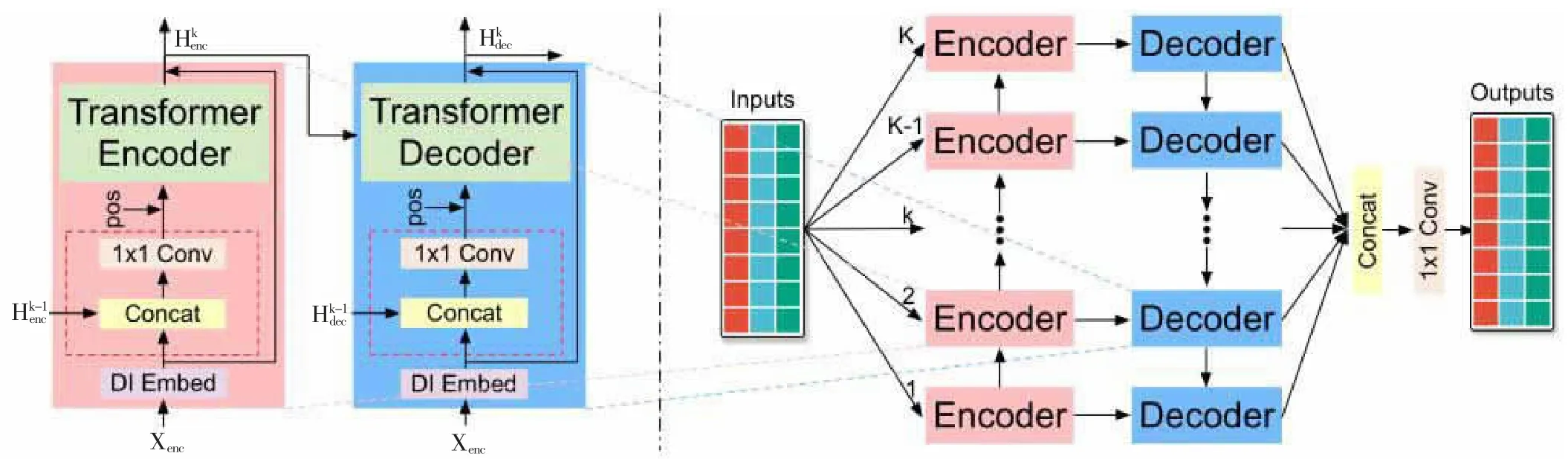
图2 算法框架
从图2 可知,MTPNet 包括多个变换器-编码器-解码器对,用于学习多个无约束尺度的时间相关性。为了实现不同粒度的建模,本文采用了patch 尺寸来控制时间粒度。K 层中每一层对应一种大小的patch size,基于这个patch size 进行DI embedding,可以实现不同粒度的信息提取。第k 层的信息会通过拼接的方式融合第k-1 层的编码结果,计算过程如下,其中H 是上一层的编码结果,X 是当前层使用对应patch size 得到的编码:
Transformer 采用的是传统的QKV 形式:
Encoder 和Decoder 都进行这种多粒度信息的建模,最终融合各个粒度的编码结构得到最终的预测结果:
3 实验验证
实验验证了本方法在测试集的预测误差,并通过与现有技术对比,证明了本文所提方法的优越性。整个误差评估实验主要包括3 个部分:①实验方案;②实验评价指标;③实验结果分析:1)基于STL 的时序数据分解实验;2)对比实验。
3.1 实验方案
本文基于变电站现场采集的数据构建建模数据集,并利用人工加差的方式构建测试数据集,通过对比预测结果与加差结果说明本方法的有效性,实验验证方案如图3所示。
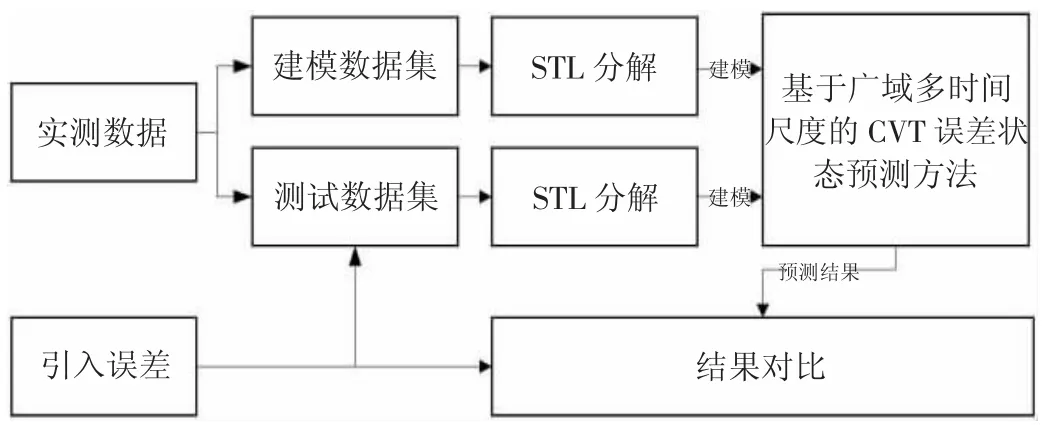
图3 实验验证方案
3.2 实验评价指标
为验证本文方法(MTPNet)的有效性,选择均方根误差RMSE 和平均绝对误差MAE 作为评价指标,RMSE 和MAE 的定义如下:
3.3 实验结果分析
3.3.1 数据来源
本实验的测试数据集采自某双母线并列运行的220kV 变电站,采样间隔为15 分钟/次,数据时间跨度为720 天,从存储数据中选择7000 点测量数据构建实验数据集,并利用软件程序直接在测试数据集的数字量上添加人为误差,构建的仿真实验用实测数据如图4 所示。
3.3.2 基于STL 的时序数据分解实验
采用STL 算法对CVT 二次输出数据进行分解,分解为周期项、趋势项、余项,如图5 所示。
3.3.3 不同输入尺度下的算法性能对比实验
为充分验证本文所提出算法模型(MTPNet)的有效性和精确性,针对同一数据集,将其切分为24 天、36 天、48天、96 天、192 天、336 天、720 天的输入长度,选择PatchTST/64、Dlinear 分别进行CVT 误差状态预测,以验证不同算法模型在误差评估问题上的准确性,对比实验结果如表2 所示。
从表2 可以看出,本文提出的算法在误差状态预测的问题上性能最佳,相比于PatchTST/64、Dlinear,RMSE 和MAE 显著降低0.7%、2.69%。
3.3.4 不同工况下的算法性能对比实验
为了进一步说明本文方法的有效性,对各个方法在不同工况下进行了前100 天的预测效果对比,如图6 所示。
从图6 可知,本文提出的算法不仅可以实时掌握CVT的动态变化趋势,还可以适应复杂工况下电压波动造成的预测曲线与实际值的偏差过大问题,适应范围广,预测精度高。
3.3.5 不同预测时间尺度下的算法性能对比实验
不同预测时间尺度下的算法性能对比实验如图7所示。
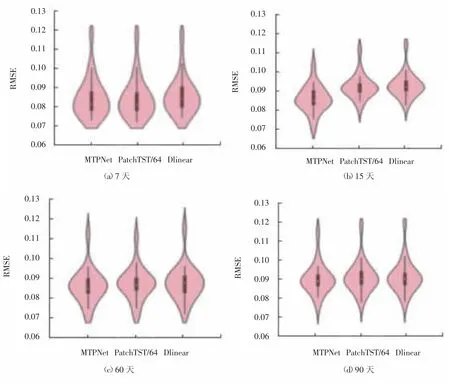
图7 不同预测时间尺度下的预测结果
本文方法在不同时间尺度预测上,预测精度和模型适应度均具有良好表现,说明本文方法在捕获二次侧输出数据的长期时间依赖性方面也具有一定的优势。
4 结语
本文提出了一种基于广域多时间尺度的CVT 误差状态预测方法,有效提高了CVT 误差状态评估精度,相关结论如下:
①深度挖掘变电站在运CVT 群体二次输出数据,提出了多时空多尺度误差状态预测技术,采用STL 将二次输出数据分解为趋势分量、周期分量和余项,构建了多元时间序列铁证;
②CVT 误差状态预测模型采用多层Transformer 结构,采用了patch 尺寸来控制,实现了任意粒度的时间序列信息建模;
③与现有的CVT 误差评估模型相比,本文所提的预测模型,能有效实现多时间尺度的CVT 误差状态预测,相比于PatchTST/64、Dlinear,RMSE 和MAE 显著降低0.7%、2.69%。
由于本方法是基于广域数据驱动方法,不依赖于物理模型,因此同样适用于CT、电能表等计量装置,具有广阔的应用前景。
