弄另水电站监测控制网稳定性研究

任威 REN Wei；宋红平 SONG Hong-ping

（①中国电建集团昆明勘测设计研究院有限公司，昆明 650000；②德宏州龙江水电开发有限公司，德宏 678400）

1 概述

水电站变形监测能够通过观测数据清晰、直观地反映被监测部位的位移情况，是水电站日常运行管理工作的重要组成部分，而变形监测控制网可以为日常变形监测提供准确、可靠的位置基准，因此，监测控制网点的稳定性对于保证监测成果的可靠性、评判水工建筑物和边坡的安全稳定状态等具有十分重要的意义[1-2]。

弄另水电站位于云南德宏傣族景颇族自治州龙江—瑞丽江中段梁河县勐养镇弄另村以东5km 的干流上，是一座以发电为主，兼有养殖、旅游等综合功能的Ⅱ等大（2）型水电工程。弄另水电站枢纽主要由碾压混凝土重力坝、引水建筑物、发电厂房等建筑物组成。总库容2.33 亿立方米，装机容量180MW。枢纽主要建筑物、挡水、泄水、冲砂建筑物和引水系统进水口建筑物为2 级建筑物，引水建筑物、发电厂房及开关站为3 级建筑物，施工导流建筑物为4 级建筑物。拦河坝采用碾压混凝土重力坝，最大坝高90.50m，坝顶长度280.00m，坝顶宽8.0m。坝体碾压混凝土29.8 万m3。坝体上游面在高程900.00m 以上直立，高程900.00m 以下坝坡为1∶0.2；坝体下游面在高程954.50m 以上直立，高程954.50m 以下坝坡均为1∶0.8。

2 监测控制网布设情况

弄另水电站平面位移监测控制网点也是日常变形监测的工作基点，控制网由8 个点组成（点号为201、202、203、204、205、206、207、JM01），主要图形为三角形、大地四边形和中点多边形，分布于枢纽区周围山坡上，左岸布置3 个控制点，右岸布置5 个控制点。所有监测控制网点均采用钢筋混凝土观测墩，墩顶安装强制对中盘。监测控制网布设等级为一等，平面坐标系统采用弄另水电站独立坐标系统，基准面（投影面）采用大坝中部高程面即919m 高程面，高程系统采用1985 国家高程基准。监测控制网布设图见图1。

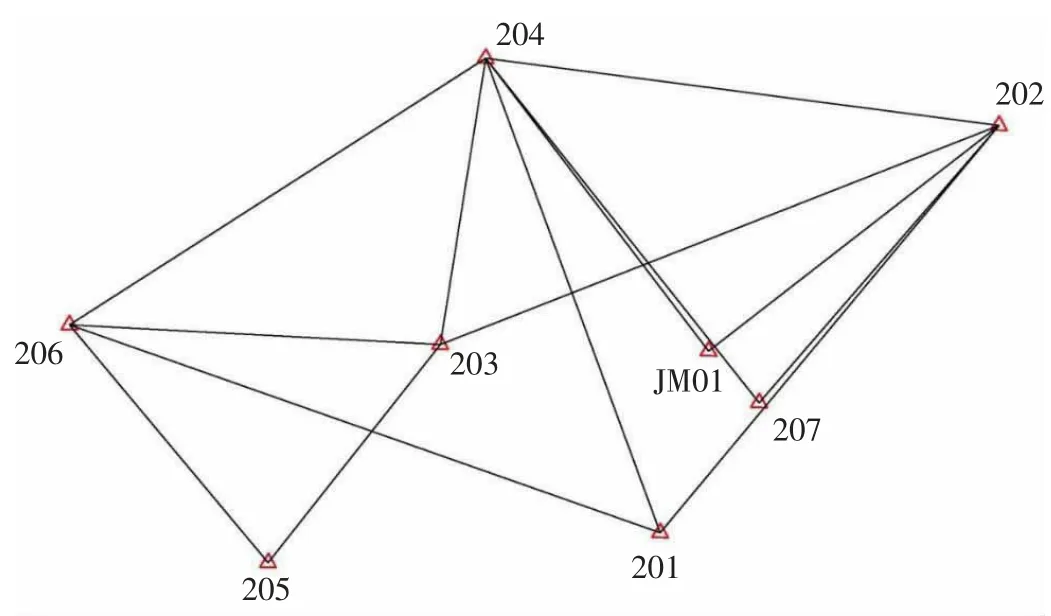
图1 弄另水电站监测控制网网形图

3 控制网复测情况

本文采用的数据为弄另水电站2022 年、2023 年监测控制网复测数据，结合2013 年控制网复测成果进行弄另水电站监测控制网稳定性分析。

弄另水电站2022 年、2023 年监测控制网复测均选取汛期来临前、水位相对稳定的5 月份进行，平面控制网测量按照一等精度进行，测量仪器采用高精度测量机器人徕卡TS60，标称测角精度为±0.5″，测距精度为±（0.6mm+1ppm×D），测量过程中同时测定温度、湿度、气压数据，以进行气象改正。

水平角观测采用全圆方向观测法，测回数为12 个测回，分两个不同时段观测，各观测6 个测回。边长观测分为两个不同时段观测，边长与方向分开观测，在同一时间段内的往测或返测，在进行方向分组观测前后各观测4 个测回。

为了能够更好地分析评价监测控制网的稳定性，每期均按照全网重心作为基准进行平差计算。按照规范要求方向先验中误差值为±0.5″，边长先验中误差值为±（1mm+1ppm）进行定权，按照最小二乘方法进行网平差计算[3-4]。

弄另水电站监测控制网测量技术路线图见图2。

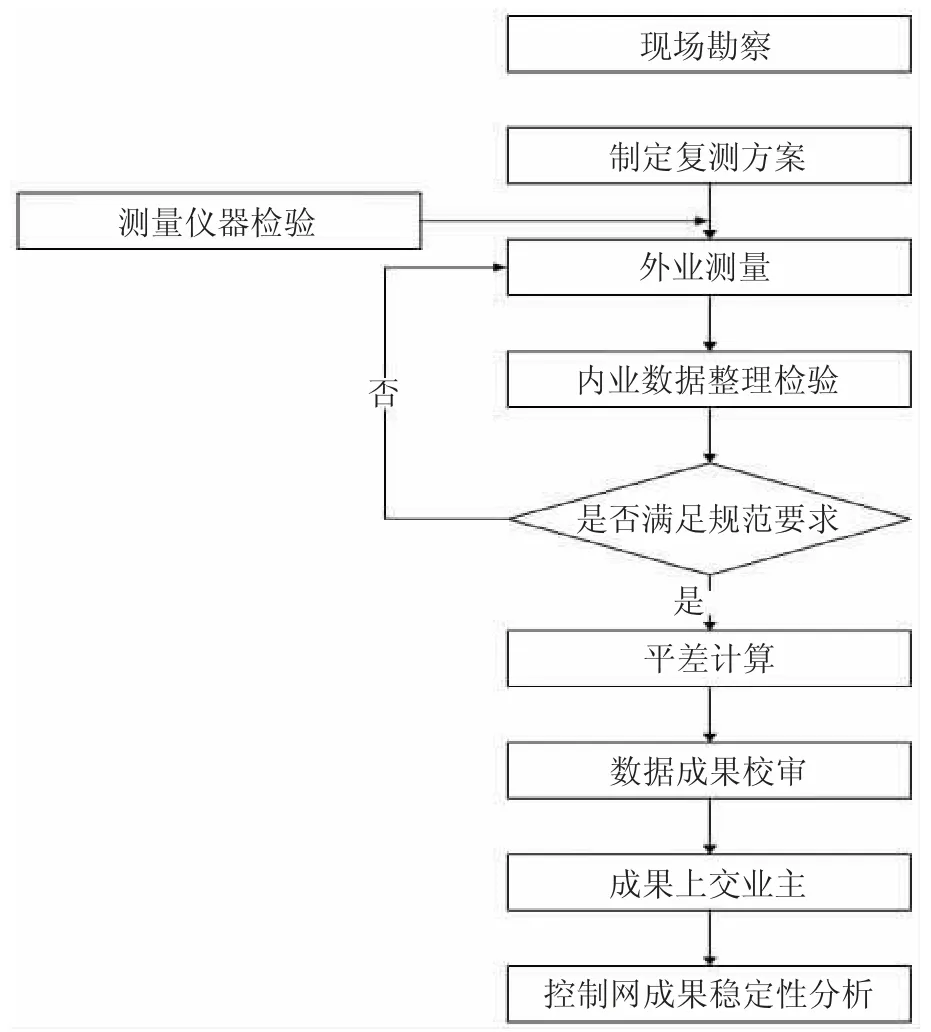
图2 弄另水电站监测控制网测量技术路线图

弄另水电站监测控制网经2022 年、2023 年两次复测，复测的精度如表1，可以看出，两次控制网复测的精度较高，满足了《水利水电工程测量规范》（SL197-2013）的要求。

表1 弄另水电站控制网复测精度

4 监测控制网稳定性分析

4.1 误差椭圆法

变形误差椭圆主要利用同一点在两期观测后得到的坐标差在不同方向上的分布规律，计算出平差后的位移矢量（Δx，Δy）及变形误差椭圆，如果位移矢量在极限变形误差椭圆内，则认为该点稳定，没有显著性位移，反之，则认为该点不稳定[5]。

两期观测后对控制网进行平差计算，得到各点的协方差矩阵，并求得变形误差椭圆，公式如下[6]：

计算出每个点的误差椭圆后，取k 倍中误差作极限误差椭圆。平面控制网观测误差一般服从二位正态分布，分布密度为：

μx、μy为数学期望，σx、σy为中误差，σxy为协方差。

用平行于XOY 的平面截取上述曲面，并将截线投影到XOY 平面，可得到一组同心椭圆：

上述椭圆即为误差椭圆，将坐标原点移到椭圆中心，再旋转θ 角，用E、F、k 分别代替σx、σy、γ，可得到一组同心椭圆Bk：

将上述公式带入二维正态分布密度函数，经简化后可得：

那么点位在误差椭圆内的概率公式为：

当k=1 时，落入误差椭圆内的概率P=0.3935；当k=2时，落入误差椭圆内的概率P=0.8647；当k=3 时，落入误差椭圆内的概率P=0.9978。根据计算概率，当k=3 时，所得椭圆即为极限误差椭圆。取长半轴3E、短半轴3F、主轴方向θ 做极限误差椭圆，当位移矢量位于极限误差椭圆内时，则认为该点没有出现显著性位移[8]。

4.2 稳定性分析

根据弄另水电站2022 年、2023 年的控制网复测数据，首先进行秩亏自由网平差计算各点的位移量，筛选出位移量较大的控制点，后进行拟稳平差，筛选出稳定的基准点组，按照拟稳平差方法求得新的基准坐标，使新基准与原基准保持一致，求得的其它点的位移量才是同一个基准下的位移量。最后进行经典自由网平差，得到2022 年、2023 年控制网复测成果并与2013 年控制网测量成果进行对比，对比结果统计见表2。

表2 弄另水电站控制网复测位移量

根据表2 的数据统计结果，2022 年的复测成果相比于2013 年的成果，点203、点204、点205、点207 的位移量相对较大；2023 年的复测成果相比于2022 年的成果，点202、点205、点206 的位移量相对较大。

因2022 年弄另水电站监测控制网网形与2013 年网形存在不同，且间隔时间较长，数据衔接性较差，进行稳定性分析的结果也不具有代表性。2023 年监测控制网复测网形与2022 年相同，使用的观测方法、观测仪器也相同，数据衔接性较好，因此根据2023 年弄另水电站复测成果采用误差椭圆法进行控制网点位的稳定性分析。

根据计算，2023 年弄另水电站监测控制网复测的点位误差椭圆见表3。

表3 弄另水电站控制网复测误差椭圆

根据表2、表3 数据，取k=3 得到极限误差椭圆，将位移量数据与极限误差椭圆进行比较，得到结果如表4。

表4 位移量与极限误差椭圆

根据表4 作出的误差椭圆与位移量并将其置于同一图形中，可以很清晰地看出点201、点204、点207、点JM01 位移量位于极限误差椭圆内，那么认为点201、点204、点207、点JM01 未出现显著性位移，点位稳定；点202、点203、点205、点206 位移量不在极限误差椭圆范围内，说明点位出现显著性位移。根据现场实际情况来看，平面位移变化最大的是位于右岸道路内侧边坡上202、206 号点和左岸的205 号点，平面变化量分别为4.66mm、3.76mm、3.22mm，位移方向为顺坡向，符合平面位移的基本趋势，与使用极限误差椭圆法进行点位稳定性分析的结果一致。（图3）

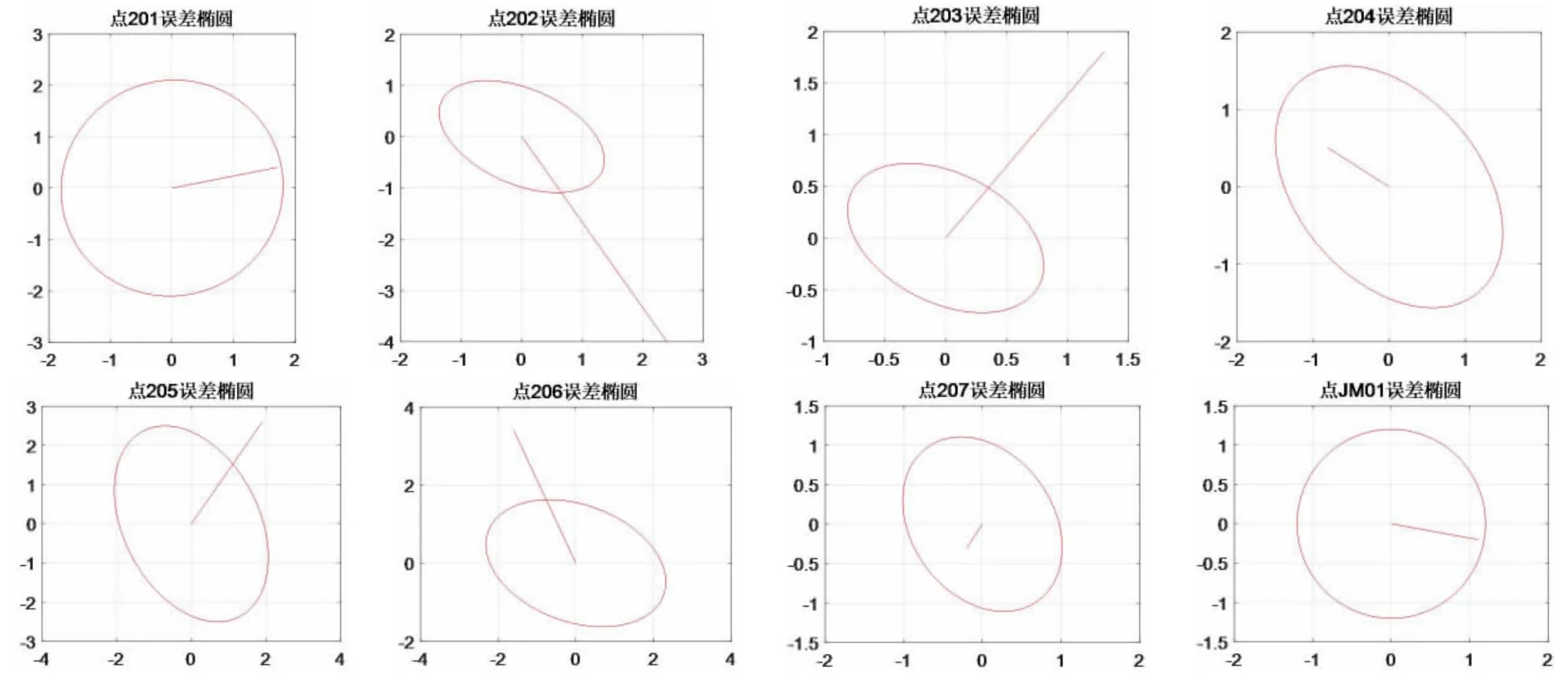
图3 各点极限误差椭圆与位移量关系图

5 结论

本文介绍了弄另水电站监测控制网布设情况及近两年的监测控制网复测成果，复测数据质量较高，各项技术指标达到规范要求。根据2022 年、2023 年复测成果使用极限误差椭圆法对控制网点进行了稳定性分析，结果显示，弄另水电站监测控制网存在显著位移点（点202、点203、点204、点206），其余各点均稳定，位移量较小。使用极限误差椭圆法进行控制网稳定性分析具有一定的实际应用价值。