二维非参数死亡率修匀模型的对比分析——基于2000—2020年中国人口死亡率数据

刘瀚文，葛建军，董 颖，李森林

（1.贵州财经大学 大数据统计学院，贵州 贵阳 550025；2.贵州省大数据统计分析重点实验室，贵州 贵阳 550025）

中国人口死亡率数据主要来源于全国人口普查和人口抽样调查，数据波动较大，故对人口死亡率修匀是十分必要的。修匀的死亡率不仅能够帮助保险公司评估保险产品的可持续性、确保盈利，还能够避免保费过高问题的出现，维护客户的利益。MILLER［1］将修匀定义为：一种可靠的方法，根据一个连续变量的不规则观察序列，用这种方法得到一个光滑的有规律的修正序列，与观察序列相和谐。从修匀的概念可以看出，修匀不仅要考虑修匀序列的光滑度，还要考虑与初始值的拟合程度。国内外关于人口死亡率修匀模型的研究主要集中于参数修匀模型和非参数修匀模型，所使用数据形式包括一维数据（考虑在年龄维度或时间维度上进行修匀）和二维数据（同时考虑年龄和时间维度）。

一、文献综述

（一）参数修匀模型

参数修匀是指在修匀过程中，用选定的特殊函数形式来表示相邻死亡率之间的先验关系［2］。Gompertz 模型［3］和Makeham 模型［4］是最早提出的死亡率修匀模型，适用于高龄组的人口死亡率修匀，对其他年龄组的人口死亡率修匀效果较差。为了满足全年龄段人口死亡率修匀的需求，HELIGMAN 和POLLARD［5］提 出 了Heligman-Pollard 模型，该模型通过增加参数的方式对Gompertz模型进行调整，填补了早期研究的空缺，并在发达国家的实证中取得了较好的效果。Carriere 模型［6］使用包含四种分布的混合参数模型来拟合美国人口死亡率，发现效果优于Heligman-Pollard 模型。以上方法是在修匀过程中函数表达式形式始终不变的整体参数修匀方法。国内的专家学者对参数修匀模型研究起步较晚，李荣敏等［7］和孙佳、吴明［8］均通过引入加权系数保证修匀结果兼具拟合度和光滑度，是一种改进的整体参数修匀方法。孙佳美、许素英［9］通过对比Heligman-Pollard 模型和Carriere模型在中国分性别全年龄段人口死亡率上的修匀效果，发现Carriere模型的拟合效果较好。

（二）非参数修匀模型

人口死亡率的非参数修匀模型主要有移动加权平均修匀模型（M-W-A）、Whittaker 修匀模型、Bayesian 修匀模型、核修匀模型等。M-W-A 模型是19 世纪提出的经典非参数修匀方法，该模型虽然计算简便，但不能进行端值修匀，且只考虑了修匀结果的拟合度。WHITTAKER［10］综合考虑修匀值的拟合度和光滑度，首次提出Whittaker 修匀模型。HENDERSON 在随后的两年对此模型作出了重大的贡献，将该模型推广到二维的情形（考虑年龄和时间）。Kimeldorf-Jones 修匀模型［11］是最早将Bayesian 修匀方法运用在人口死亡率修匀中的模型。COPAS 和HABERMAN［12］提出了核修匀方法，弥补了M-W-A 模型不能得到端值修匀值的缺陷，且可通过计算机进行高效运算。GAVIN、HABERMAN 和VERRALL［13］将核函数设置为对称函数，同样能够解决端值问题，但存在边界偏差的现象。张志强、谭鲜明和朱建平［14］基于COPAS 和HABERMAN 提出的核修匀模型，用Gamma 核来替换对称核函数，解决了边界偏差问题，并取得了较好的效果。MAZZA 和PUNZO［15］提出的离散Beta 核修匀模型通过设置非对称核函数同样解决了边界偏差的问题。

在现实的人口死亡率修匀应用中，通常需要同时考虑年龄和时间对死亡率变化趋势的影响，故关于二维修匀方法的研究应运而生。LEE 和CARTER［16］基于年龄和年份提出的动态死亡率模型可用于二维死亡率修匀。HABERMAN、RENSHAW［17］使用广义线性模型（GLM）对人口死亡率进行修匀，不仅研究了人口死亡率与年龄、年份两因子的关系，还研究了人口死亡率与年龄、保单期限两因子的关系。张连增、段白鸽［18］基于GLM 模型对比了泊松回归模型和负二项回归模型的拟合效果，发现负二项回归模型的拟合效果较好，同时也证实了二维非参数修匀模型在中国人口死亡率修匀上有一定的适用性。近些年，核方法和光滑样条法在人口死亡率修匀中得到了较好的应用［19］。MAZZA、PUNZO［20］拓展的二维离散Beta 核修匀模型和DJEUNDJE、CURRIE［21］提出的二维泊松P-样条修匀模型作为核方法和光滑样条法的代表，在多个国家的人口死亡率修匀中表现良好。赵明［19］通过对比二维离散Beta 核方法和二维泊松P-样条方法在中国男性人口死亡率上的修匀效果，发现两种二维非参数修匀模型各有优劣。

（三）文献述评

由于人口死亡率年龄跨度长，不同年龄段人口的生命特征存在较大差异，参数修匀方法需要针对不同年龄段分别建模，模型扩展能力较弱，且不能较好地反映人口死亡率随时间改善这一趋势。因此，本文认为二维非参数修匀方法更适合对全年龄段的动态生命表进行修匀。国内现有的研究均未将传统的二维非参数修匀方法加入模型对比中，且应用范围多为某一具体人口群体，缺乏对模型修匀效果的城乡及性别差异的研究［19］。故本文将传统的二维Whittaker 修匀模型以及近些年应用效果较好的二维离散Beta 核修匀模型和二维泊松P-样条修匀模型进行对比，分析各模型在中国分城乡、性别人口死亡率上的修匀效果。

二、模型简介

（一）二维Whittaker修匀模型

Whittaker 修匀方法同时考虑了修匀值的拟合度和光滑度。两个指标并非相互独立的，较高的拟合度会导致光滑度较差，较好的光滑度会使模型的拟合度受到损失。为了兼顾修匀结果的拟合度和光滑度，采用线性加成的方法对模型的修匀效果进行评估，二维Whittaker修匀模型如下式：

假设死亡率矩阵是m×n的（m为年龄范围，n为年份范围），uij表示在第j年i岁的人口死亡率，vij是模型修匀后的死亡率(i=1,2,……m,j=1,2,……n)。wij是拟合度量因子的权重，反映了原始的死亡人数和修匀后死亡人数的差别。是年龄维度光滑度度量的差分算子是时间维度光滑度度量的差分算子。α和β分别为年龄维度和时间维度的光滑水平权重。通过极小化M，就可以求出修匀后的死亡率vij。

（二）二维离散Beta核修匀模型

设d(x,y)为第y年x岁的死亡人口数，e(x,y)为第y年x岁的平均人口数，q(x,y)为第y年x岁真实但未知的人口死亡率为第y年x岁的粗死亡率，d(x,y)服从二项分布，即d(x,y)～B[e(x,y),q(x,y) ]［22］。q(x,y)的Nadaraya-Watson核估计量如下式所示：

设Z是有序且等间距的二维离散随机变量，记为集合Z={aZ,bZ}，cz=bz-az，hz为带宽。二维离散Beta核函数如式（3），标准形式见式（4）。

二维离散Beta核修匀的自适应带宽为：

（三）二维泊松P-样条修匀模型

KEIDING［23］认为在第j年i岁的死亡人口数服从泊松分布，即Yij～P(Eij,uij)。其中，Eij是第j年i岁的平均人口数，uij是第j年i岁人口的死亡率。用m×n的矩阵形式分别表示死亡人口数和平均人口数，记为Y和E。其中，矩阵行m表示年龄，矩阵列n表示年份。死亡人数和平均人口数向量分别表示为y和e。

在二维泊松数据上进行P样条修匀，需构造一个二维回归的B-样条作为回归基，可表示为克罗内克乘积：B=By⊗B（a基于年龄维度的m×ka回归矩阵Ba和基于时间的n×ky回归矩阵By）。a 是与每条B样条相关联的参数，将a 的元素排列成为一个ka×ky的矩阵A，即a=vec(A)。同理y=vec(Y)，e=vec(E)。故二维泊松P-样条修匀模型可表示为以下形式：

EILERS 和MARX［24］研究表明，可以选择一个相对较大的B样条，同时为了防止大的回归基导致过拟合，可在样条的系数a 上加一个额外的惩罚项P，使系数变化更加平稳。故定义差分矩阵Da和Dy，在样条系数矩阵A的行与列上分别添加惩罚项，如式（8）所示：

其中，λa和λy分别是年龄维度和时间维度上的平滑参数，I表示单位阵。可利用迭代重加权最小二乘法（IRWLS）计算系数a，详见CAMARDA［25］。

三、三种二维非参数死亡率修匀模型对比

（一）数据来源与预处理

1.数据来源

本文使用的2000—2020 年分城乡、性别的全年龄段人口死亡率数据来源于2001—2006 年的《中国人口统计年鉴》和2007—2021 年的《中国人口和就业统计年鉴》。

2.数据预处理

（1）将城市与镇的“分年龄、性别死亡人口状况”数据合并，乡村数据不变。

（2）全国人口普查年份和1%人口抽样调查年份的死亡率年龄上限为100+岁（尾数逢0 和5 的年份），为了统一各年的年龄范围，将死亡率年龄上限调整为90+岁，与全国1‰人口抽样调查的死亡率年龄上限保持一致。

（3）按照各年实际抽样比，将全国1%人口抽样调查数据和1‰人口抽样调查数据调整为和全国人口普查数据同一量级。

（4）将各年分城乡、性别的全年龄人口死亡率数据分别合并。采用在时间维度上进行线性插值的方法来解决人口抽样调查年份的数据缺失问题。

表1 2000—2020年人口抽样调查比

（二）死亡率修匀的光滑度对比

图1—图4 分别展示了2000—2020 年城镇男性、城镇女性、乡村男性和乡村女性的全年龄段（0 岁～90+岁）粗死亡率与修匀后死亡率的变化趋势。三种二维非参数修匀模型在2000—2020 年分城乡、性别的人口死亡率修匀中均表现出了一定的修匀效果。在各人口群体中，二维Whittaker 修匀结果的光滑度最佳。但在不同年份的城镇女性5岁～7岁组、乡村男性5岁～7岁组及乡村女性4岁～8岁组会出现一些负值（为了便于展示，将所有负值调整为0）。

图1 城镇男性死亡率修匀结果的光滑度对比

图2 城镇女性死亡率修匀结果的光滑度对比

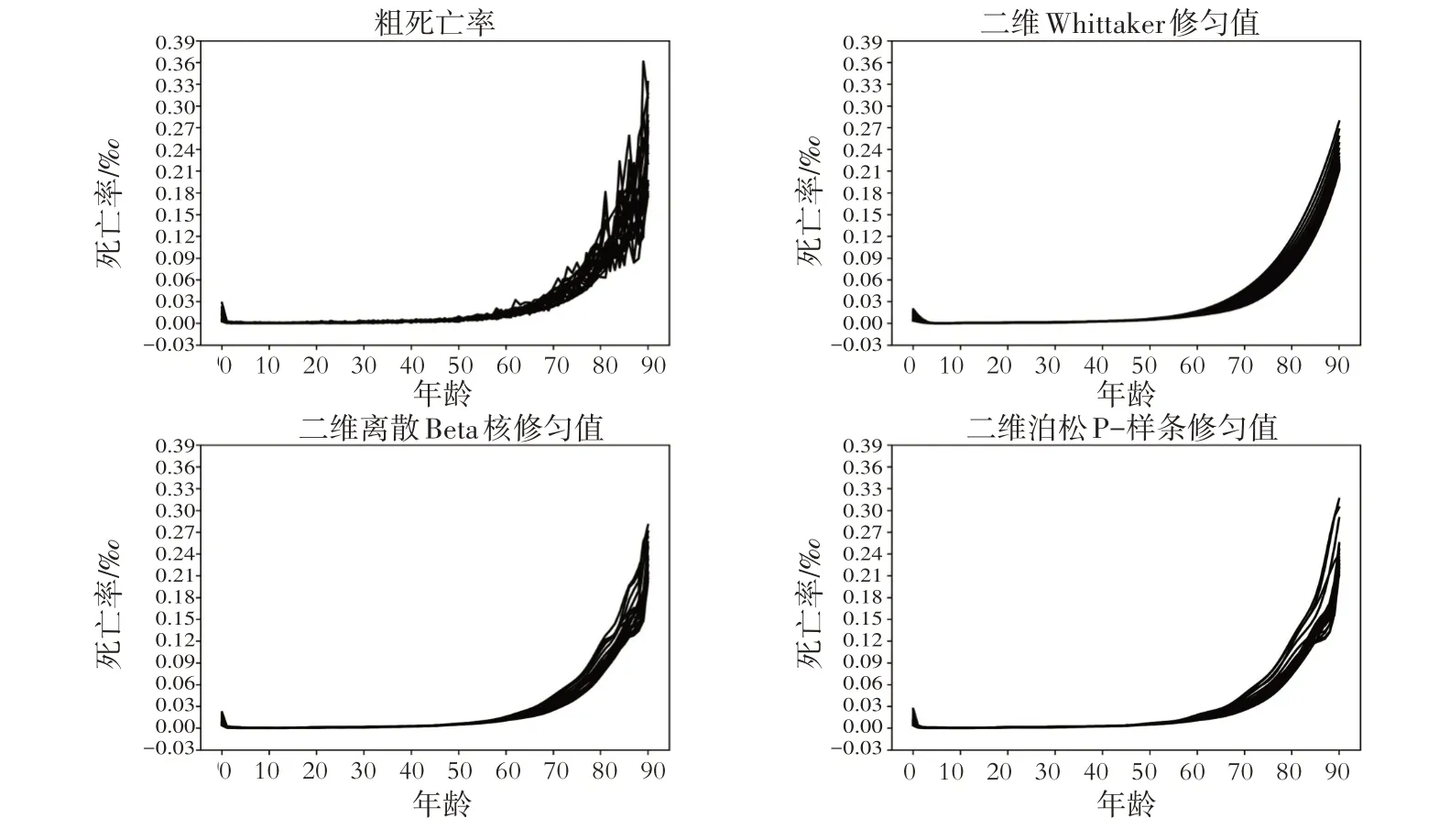
图3 乡村男性死亡率修匀结果的光滑度对比

图4 乡村女性死亡率修匀结果的光滑度对比

除了修匀光滑度表现最佳的二维Whittaker 修匀模型以外，二维泊松P-样条修匀模型在城镇男性和城镇女性死亡率修匀上表现出良好的光滑度，二维离散Beta 核修匀模型次之。对比乡村人口死亡率修匀效果发现，二维离散Beta核修匀模型和二维泊松P-样条修匀模型的修匀结果光滑度表现良好，且无显著差异。

（三）模型在边端年龄处的修匀效果对比

在对死亡率进行修匀时，还要适当考虑模型对边端年龄的修匀效果。张为民和崔红艳［26］指出，第五次全国人口普查死亡率漏报率约为8%。张文娟和魏蒙［27］的研究发现，在第六次全国人口普查数据中婴幼儿和老龄人口存在严重的死亡漏报。李婷、郑叶昕和闫誉腾［28］的研究结果显示，在第七次全国人口普查中，婴儿死亡漏报率在70%以上，老龄人口死亡率也有漏报问题。综上所述，研究人员发现近三次全国人口普查均出现低龄人口和老龄人口死亡率漏报的现象。边端年龄人口的死亡率本就可能存在漏报现象，如果修匀模型严重低估边端年龄处的死亡率，将会影响对未来人口死亡率发展趋势的判断。故对比不同模型在各人口群体中的边端年龄修匀效果十分有必要。

通过观察图1-图4发现，三种二维非参数修匀模型在修匀边端年龄时均存在低估的现象，但是各人口群体的低估程度稍有不同。具体来看，二维Whittaker 修匀模型在低龄组和高龄组的修匀效果过于平滑，导致低龄及高龄组的死亡率被远远低估。二维离散Beta 核修匀模型在修匀城镇人口的边端年龄死亡率时，其结果更靠近真实值；二维泊松P-样条修匀模型在修匀乡村人口的边端年龄死亡率时，其结果要更贴近真实值。

（四）死亡率修匀的拟合度对比

死亡率修匀的拟合度检验借助TSAI、LIN［29］的平均绝对百分比误差方法（AMAPE），其中[T1,T2]指代的是年份范围，[t1,t2]指代的是年龄范围。代表在x年y岁死亡率的修匀值，mx,y代表在x年y岁的粗死亡率。AMAPE 的值越小，代表死亡率修匀的拟合效果越佳。

1.总体拟合效果对比

在分城乡、性别的模型拟合度对比中，二维离散Beta核修匀模型展现了最好的总体拟合效果，其次是二维泊松P-样条修匀模型，最差的是二维whittaker修匀模型（见表2）。因为人口粗死亡率的“噪声点”较多，经模型修匀以后，死亡率的变化趋势更符合现实规律，故导致三种模型的AMAPE 值普遍较大。

表2 三种修匀模型的拟合度对比（占比/%）

2.不同年份的拟合效果对比

观察各年分城乡、性别的模型拟合度发现，二维离散Beta 核修匀模型展示了最好的拟合效果。在全国人口普查年份2000 年和2020 年，城镇人口死亡率修匀结果的拟合度要明显优于其他年份；在普查年份2000、2010和2020年，乡村人口死亡率修匀结果的拟合度也要明显优于其他年份，即普查年份的人口粗死亡率数据异常波动更小（见表3）。同样，全国1%人口抽样调查年份（尾数逢5 的年份）的修匀结果拟合度普遍优于全国1‰人口抽样调查年份（除了尾数为0 和5 的剩余年份），从侧面反映出全国人口普查的人口死亡率数据质量优于全国1%人口抽样调查数据，全国1‰人口抽样调查的数据质量次之。

表3 各年分城乡、性别的模型拟合度对比（占比/%）

3.不同年龄的拟合效果对比

对比各年龄分城乡、性别的模型拟合度发现，除了乡村人口的0 岁组以外，二维离散Beta 核修匀模型在所有年龄组的拟合效果都是最优的。60 岁以上年龄组的修匀结果拟合度普遍优于其他年龄组（见表4）。

表4 各年龄分城乡、性别的模型拟合度占比

四、结论

通过对比二维Whittaker 修匀模型、二维离散Beta 核修匀模型和二维泊松P-样条修匀模型在2000—2020 年中国分城乡、性别人口死亡率上的修匀效果，得出以下结论。

1.三种死亡率修匀模型的结果均具有一定的光滑度，但光滑效果存在差异。二维Whittaker 修匀模型的修匀结果的光滑度最好，代价是损失了部分真实信息，导致城镇女性和乡村人口的死亡率修匀结果出现负值。在对城镇人口死亡率进行修匀时，二维泊松P-样条修匀结果的光滑度要优于二维离散Beta 核修匀模型。在对乡村人口死亡率进行修匀时，二维离散Beta 核修匀结果和二维泊松P-样条修匀结果的光滑度无显著差异。

2.从总体上看，二维离散Beta核修匀模型具有最好的拟合度。从年龄和时间两个维度来对比三种模型在各人口群体上的修匀结果拟合度发现，二维离散Beta 核修匀模型的修匀结果不仅在各年份上获得了最优的拟合度，在除0 岁组乡村人口以外的其他年龄组也获得了最优的拟合度。

3.三种死亡率修匀模型均存在低估边端年龄死亡率的问题，但低估程度略有差异。观察各模型在边端年龄处的死亡率修匀效果发现，二维离散Beta 核修匀模型在城镇人口的边端年龄修匀结果更靠近原始值，二维泊松P-样条修匀模型在乡村人口的边端年龄修匀结果更靠近原始值。

在进行人口死亡率修匀时，应权衡模型光滑度和拟合度的效果。根据不同模型的特点，选择一种或多种模型进行人口死亡率修匀。文章只对较为经典的二维Whittaker修匀模型以及近些年在多个国家人口死亡率数据上得到验证的二维离散Beta核修匀模型和二维泊松P-样条修匀模型进行了比较，后期研究应将更多人口死亡率修匀模型进行对比，探究各模型在中国人口死亡率修匀上的适用性。