Two-proton radioactivity from excited states of proton-rich nuclei within Coulomb and Proximity Potential Model

De-Xing Zhu · Yang-Yang Xu · Li-Jia Chu · Xi-Jun Wu · Biao He · Xiao-Hua Li,5,6,7

Abstract In the present work, we extend the Coulomb and Proximity Potential Model (CPPM) to study two-proton (2p) radioactivity from excited states while the proximity potential is chosen as AW95 proposed by Aage Withner in 1995.Demonstration reveals that the theoretical results acquired by CPPM exhibit a high level of consistency with prior theoretical models such as the unified fission model (UFM), generalized liquid-drop model (GLDM) and effective liquid-drop model (ELDM).Furthermore, within the CPPM, we predicted the half-lives of potential 2p radioactive nuclei for which experimental data are currently unavailable.The predicted results were then assessed, compared with UFM, ELDM and GLDM models, and examined in detail.

Keywords 2p radioactivity · CPPM · Half-lives · Excited state

1 Introduction

Except for the well-knownα,β,γand cluster decays, etc.[1–10], there exist some exotic modes of radioactivity in proton-rich nuclei [11–13], such as proton and two-proton(2p) radioactivity [14–18].2p radioactivity is an extremely exotic mode that is energetically possible in less massive nuclei near the proton-drip line [19–25], and it can reveal abundant information of nuclear structure, including the nuclear radius, wave function of the emitted two protons,spin and parity, deformation effect and so on [26–28].This novel decay mode was firstly predicted by Zel’dovich and Goldansky in 1960s [29–31].Based on the pioneering work of Zel’dovich and Goldansky, an extensive range of theoretical models have been proposed to describe this exotic decay process [32–35].However, due to the limitations in radioactive beam facilities and detection technology, 2p radioactivity was not experimentally confirmed until the observation of45Fe →43Cr+p+p decay by Giovinazzo et al.at GANIL (France) and independently by Pfützner et al.at GSI (Germany) in 2002, which provided the first experimental evidence of this decay mode [36, 37].Since then 2p radioactivity has been recognized as the significant decay mode for proton-rich nuclei [38], and it has been detected and studied in several nuclei, such as the resonant ground state of6Be [39, 40] and12O [41], and in the excited state selectively populated in6Be [40] and14O [42], etc.

Numerous studies have shown that the 2p radioactivity not only occurs from ground state but also from short-lived excited state.Jänecke was the first to discuss the possibility ofβ-delayed 2p (β2p ) radioactivity [38], while Goldansky predicted the occurrence ofβ2p radioactivity could be found inβ2p emitters ofZ=10-20.In 1983, Cable et al.reported the first experimental observation ofβ2p radioactivity [43].Subsequently, an increasing number ofβ2p emitters have been detected using silicon detector telescopes, making it possible to measure the energy of two individual protons with high precision.Since Cable et al.[43] discovered theβ2p radioactivity from22Al, shortly they observed moreβ2p radioactivity from26P [44] and35Ca [45].Hereafter, several otherβ2p nuclei were found, including23Si [46],27S [47],31Ar [48],39Ti [49],43Cr [50, 51] and50Ni [52].In addition to populating excited state 2p radioactivity viaβdecays, 2p radioactivity has also been observed from excited state fed by nuclear reactions such as pick up, transfer or fragmentation, including14O [42],17,18Ne [53–57],22Mg [58, 59] and28,29S [60, 61].In 2006, Mukha et al.first reported 2p radioactivity from94Ag in an experiment at GSI [62].

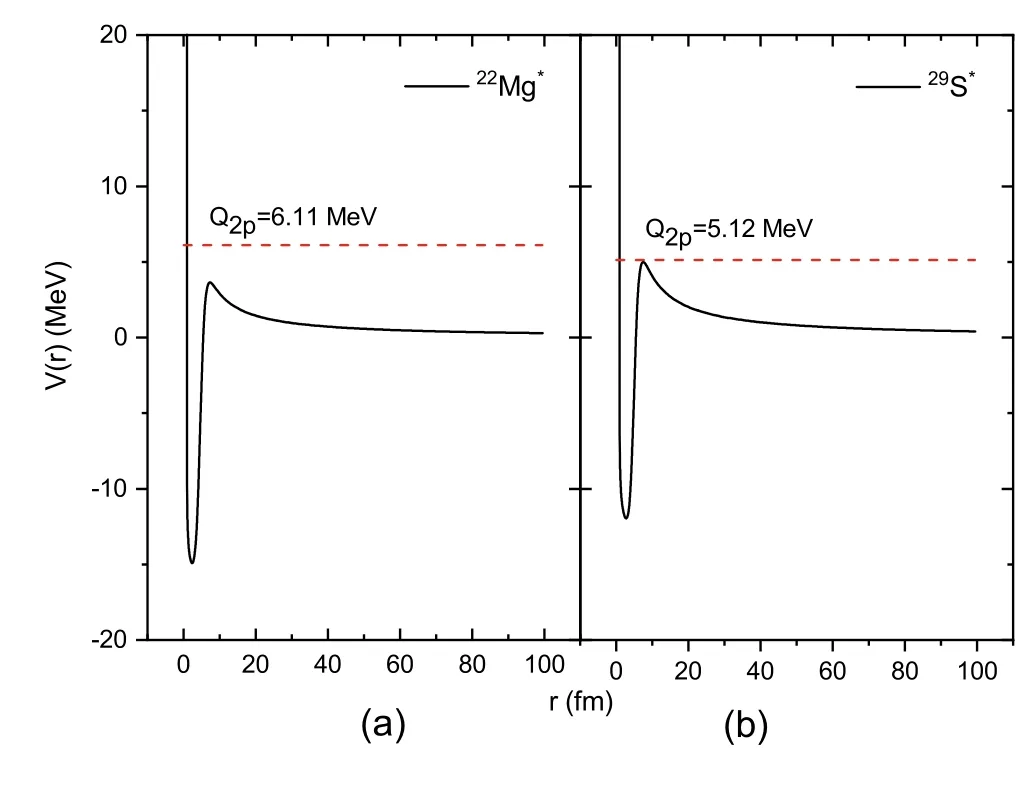
From a theoretical perspective, several methods have been proposed over the past few decades to study the mechanism of 2p radioactivity, including both microscopic and phenomenological models.In general, there are three distinct ways for proton-rich nuclei to emit two protons: (1) two-body sequential emission, (2) three-body simultaneous emission and (3) diproton emission (also called2He cluster emission).The2He cluster emission is an extreme scenario with the two strongly correlated protons that can only survive for a brief time before splitting after passing through the Coulomb barrier.Recently, based on the CPPM, Yao et al.[64] and Ghodsi et al.[65], as well as Deng et al.[66] and Santhosh et al.[67], performed comparative studies of various proximity potential formalisms to studyαdecay, proton radioactivity and cluster radioactivity, respectively.Considering that the 2p radioactivity decay process shares the same theory asαdecay and proton radioactivity, i.e., barrier penetration[68–73], we extended the CPPM presented in Ref.[74] to account for ground state 2p radioactivity.It was found that both the calculated and predicted results were highly consistent with experimental data and results from other theoretical models.In fact, except for theoretical models the empirical formulae are excellent tools for investigating 2p radioactivity involving a four-parameter empirical formula provided by Sreeja et al.[34] and a two-parameter empirical formula proposed by Liu et al.[63].Consequently, a desirable question is whether 2p radioactivity from excited states can be regarded as2He cluster emission and described by the CPPM.To address this question, we systematically studied the half-lives of 2p radioactivity from excited states within the CPPM for nuclei with 8

This paper is organized as follows: In Sect.2, the theoretical framework of 2p radioactivity half-life and the CPPM formalism are described briefly.In Sect.3, detailed calculations and discussion are presented.Finally, a summary is given in Sect.4.

2 Theoretical framework

2.1 The 2p radioactivity half-life formalism

In CPPM, the nuclear potential is replaced by proximity potential.A detailed description of the proximity potential will be provided in Sect.2.2.

Assuming a homogeneous spherical charge distribution for the daughter nucleus, the Coulomb potentialVC(r) is postulated to be the potential of a uniformly charged sphere with radiusR.It is expressed as follows:

where ℓ is the orbital angular momentum taken away by the emitted two protons.

2.2 The proximity potential formalism

The phenomenological proximity potential was first proposed by Blocki et al.[77] in 1970s for heavy-ion reactions.It provides a simple formula for the nucleus–nucleus interaction energy as a function of the separation between the surfaces of the approaching nuclei, with adjustable parameters that makes use of the measured values of the nuclear surface tension and surface diffuseness.In the CPPM, the potential energy barrier is modeled as the sum of Coulomb potential, proximity potential and centrifugal potential for both the touching configuration and separated fragments.In this work, we select the AW95 proposed by Aage Withner in 1995 [78] as an example to replace nuclear potential.This set of proximity potential can be expressed as

where the coefficientsγ0= 0.95 MeV/fm2andks= 1.8.HereAi,ZiandNi(i=1,2 ) are the mass number, proton number and neutron number daughter nucleus and emitted two protons, respectively.

3 Results and discussion

Blocki first presented the proximity potential in 1977 to characterize the interaction potential between any two nuclei in the separation degree of freedom, based on the proximity force theorem [77].Hence, numerous nuclear proximity potentials have been widely used in nuclear physics research [79–83].The CPPM is a phenomenological model that is commonly used to study the two-body problem in the context of 2p radioactivity.It considers the interaction potential between the parent and daughter nuclei as the sum of the nuclear potential, Coulomb potential and centrifugal potential.Unlike other models, the CPPM utilizes the proximity potential, which replaces the nuclear potential with a simplified formalism based on the proximity force.This provides the model with the advantage of adjustable parameters, making it simple yet accurate.In our previous work [74], we extended the CPPM to study 2p radioactivity from the ground state, the main intention of this work is to further extend the CPPM to investigate 2p radioactivity from excited states.

Firstly, we performed the calculations on 2p radioactivity half-lives for14O∗,17Ne∗,18Ne∗,22Mg∗,29S∗and94Ag∗(∗represent the excited state), all of the calculated results are listed in Table 1.In this table, the former four columns represent the 2p decay process, experimental 2p radioactivity released energy, spin and parity of the initial and final state of the nucleus, angular momentum taken away by the emitted two protons, respectively.The fifth column is the experimental half-lives of 2p radioactivity of excited state.From the sixth to ninth columns, they represent the logarithmic form of 2p half-lives obtained by CPPM, ELDM,GLDM and UFM, respectively.In general, from this table,it is obviously seen that the theoretical half-lives obtained by CPPM are highly consistent with other theoretical models,except for the nuclei22Mg∗(with theQ2p=6.11 MeV) and29S∗(with theQ2p=5.12 MeV).In order to intuitively explain this phenomenon, we plot the interaction potential curve of22Mg∗and29S∗in Fig.1.In Sect.2.1, the half-lives of 2p radioactivity are depended on penetration probabilityPwhich is obtained by Eq.3 and conditionsV(rin)=V(rout)=Q2p.

Unfortunately, in Fig.1, the whole interaction potential curve of22Mg∗and29S∗can’t satisfied the conditions mentioned above, so that we can’t calculate correspondingP, naturally, the half-lives can’t be obtained.

Fig.1 (Color online) The whole interaction potential of 22Mg∗ and 29 S∗

Fig.2 (Color online) Comparing the half-lives of the nuclei which obtained by CPPM in Table 1 with other theoretical models

For the reason of this phenomenon, we turn our attention to remarkable deformation effect.In fact, the half-lives of 2p radioactivity are highly sensitive to proton–proton interaction due to the paring effect of valence protons.The quasi-classical2He model can’t account for the experimentally observed proton–proton correlations, which indicate back-to-back proton emission.Moreover, for the nucleus22Mg∗and29S∗, their spin-parity of the initial state of the parent nuclei are uncertain, and the values ofQ2pare floating,all of these factors have nonnegligible impact onV(r) curve.

In order to describe the agreement of the half-lives for the 2p radioactivity of excited state which calculated by CPPM,partial theoretical results are plotted in Fig.2.In this figure, the logarithmic half-lives of the 2p radioactivity of excited state obtained by ELDM, GLDM and UFM are compared with our calculations [84, 85].For the14O∗, in Table 1, its experimental data are given as log10T1∕2> -16.12 s, the calculated halflives by CPPM are very close to those from ELDM, GLDM and UFM, simultaneously the calculated results are better than from the some empirical formulas such as R-matrix theory[42], Sreeja formula and Liu formula [85], whose half-lives are -18.12 s, -19.94 s and -16.85 s, respectively.In order to intuitively discuss the influence of angular momentum ℓ and release energyQ2pon the half-lives of the 2p radioactivity from excited state, we select14O∗and94Ag∗as an example to analyze their contribution to the half-lives.In Table 1, it is obviously found that the half-lives of14O∗obtained by CPPM for the same value of ℓ nearly have three magnitudes deviation with different released energyQ2pvalue (Q2p=1.20 MeV andQ2p=3.15 MeV).Simultaneously, for the94Ag∗, identicalQ2pbut different ℓ also have three magnitudes, while the value of angular momentum are 6–10.In fact, this conclusion is same with our previous work [87].It is obviously found that eitherQ2por ℓ has a nonnegligible contribution to the14O∗and94Ag∗for their corresponding theoretical half-lives within CPPM,ELDM and GLDM.The reason for this phenomenon is the theory of these models are similar, the penetration probabilityPare calculated by WKB approximation.In other word,these theoretical models have a strong dependency withQ2pand ℓ , and we suspect the corresponding experimental data are not precise enough.Configuration mixing and three-body dynamics are commonly utilized in nuclear and molecular physics to describe systems with numerous interacting particles.However, due to the limitations of the phenomenological theoretical model, which fails to account for configuration mixing and three-body dynamics, our calculations treat the two emitted protons as strongly correlated, thus reducing them to a two-body problem.As a result, CPPM cannot provide comprehensive information on particle dynamics.Up to now,the experimental 2p radioactivity data of excited state are rare,the reason is that it is hard to observe this decay process due to the extremely short half-lives.From the scheme of these excited nuclei, it is evident that one-proton (1p) radioactivity also exists alongside two-proton radioactivity during their decay process, as well as three-proton (3p) radioactivity decay process.Therefore, the branching ratios between 1p and 2p decay serve as a crucial index for comprehending the abundant information on nuclear structure of these nuclei and merit further investigation.

4 Conclusion

In this work, we extend the CPPM to study the excited 2p radioactivity of14O∗,17Ne∗,18Ne∗,22Mg∗,29S∗and94Ag∗.It is found that the theoretical values obtained by CPPM are highly consistent with corresponding experimental data andtheoretical values obtained by ELDM and GLDM.For the nuclei22Mg∗and29S∗(with theQ2p=5.12 MeV), the CPPM is not suitable, the reason for this phenomenon perhaps caused by the angular momenta are not available because the spin-parity of the initial state of the parent nuclei has not determined.In addition, the uncertain values ofQ2palso provided strong influence on calculated results.Simultaneously, it is found that the half-lives of excited 2p radioactivity have a strong relationship withQ2pand ℓ.Comparing with the theoretical results obtained by ELDM, GLDM and UFM, the half-lives of the excited 2p radioactivity by CPPM are reliable, it maybe as a positive guideline for future experiments.

Table 1 Comparison between the experimental 2p radioactivity half-lives of excited state and those within different theoretical models

Author contributionsAll authors contributed to the study conception and design.Material preparation, data collection and analysis were performed by Yang-Yang Xu, Li-Jia Chu, Xi-Jun Wu, Biao He and Xiao-Hua Li.The first draft of the manuscript was written by De-Xing Zhu,and all authors commented on previous versions of the manuscript.All authors read and approved the final manuscript.

Data availabilityThe data that support the findings of this study are openly available in Science Data Bank at https:// www.doi.org/ 10.57760/ scien cedb.j00186.00160 and https:// cstr.cn/ 31253.11.scien cedb.j00186.00160.

Declarations

Conflict of interestThe authors declare that they have no competing interests.