Dynamic scaling characteristics of single-phase natural circulation based on different strain transformations

Jia-Ning Xu · Xiang-Bin Li · Zhong-Yi Wang · Yu-Sheng Liu · De-Chen Zhang · Qiao Wu

Abstract To understand the dynamical system scaling (DSS) analysis theory, the applicability of DSS β- and ω-strain transformation methods for the scaling analysis of complex loops was explored.A simplified model consisting of two loops was established based on the primary and secondary sides of a nuclear reactor, and β- and ω-strain transformation methods were used to analyze the single-phase natural circulation in the primary circuit.For comparison with the traditional method, simplified DSS β- and ω-strain methods were developed based on the standard scaling criterion.The strain parameters in these four methods were modified to form multiple groups of scaled-down cases.The transient process of the natural circulation was simulated using the Relap5 code, and the variation in the dynamic flow characteristics with the strain numbers was obtained using different scaling methods.The results show that both the simplified and standard DSS methods can simulate the dynamic characteristics of natural circulation in the primary circuit.The scaled-down cases in the simplified method exhibit the same geometric scaling and correspond to small core power ratios.By contrast, different scaled-down cases in the standard DSS method correspond to different geometric scaling criteria and require more power.The dynamic process of natural circulation can be simulated more accurately using the standard DSS method.

Keywords Dynamical system scaling analysis · β-strain transformation · ω-strain transformation · Natural circulation

1 Introduction

Scaling analysis is an important method for the safety analysis of nuclear power plants.In most cases, using full-scale experimental facilities is unnecessary.It is typically used in engineering to obtain a set of scaling criteria and establish experimental facilities based on these criteria.Several experimental facilities have been designed and utilized for this purpose [1].Examples include the loss of fluid test (LOFT)[2, 3], Purdue University multidimensional integral test assembly (PUMA)[4–6], Simulatore per Esperienze di Sicurezza (SPES) [7], and advanced core-cooling mechanism experiment (ACME)[8, 9] facilities.To continuously improve thermal–hydraulic experimental facilities, scaling analysis methods have also been developed,including linear scaling [10], power–volume [11, 12], and threelevel scaling analysis [5] methods.Zuber et al.[13] proposed the H2TS analysis method to analyze more complex fluid systems, particularly, the comprehensive multiphase flow systems.The scaling analysis of each component of the model system was performed using the phenomena identification and ranking table (PIRT) [14–16].To obtain various scaling analysis methods, there are a series of treatments for the system balance equations [8, 17, 18].Ishii et al.[19–21] obtained the scaling criteria for single- and two-phase natural circulations based on the natural circulation in rectangular loops by dimensionless processing of the governing equations.Lu et al.[22, 23] further discussed natural circulation on this basis, and a set of scaling criteria applicable to both single- and two-phase systems was summarized.

Table 1 Scaling methods based on two-parameter transformations

The transient condition of the reactors is an important research direction [24, 25].In recent years, a series of new methods have been proposed to measure the dynamic process of thermal fluid phenomena [26, 27].Zuber et al.[28]developed a fractional scaling analysis (FSA) method, in which the time process was expressed using the geometric size and flow properties of the model.This method can be used to study relatively complex accident transient states[29].Based on the H2TS and FSA methods, Reyes proposed a new dynamic scaling analysis theory [30].Five scaling criteria were obtained by expressing the physical process as a two-parameter affine transformation in a normalized coordinate system.Compared to traditional methods, the DSS method can optimize the simulation of dynamic processes.Li et al.[31] used the DSS method to analyze the gravity-driven drainage process.On this basis, the singlephase natural circulation in a simple rectangular loop was studied using DSS identity transformation[32, 33].Liu et al.[34] used the dynamic scaling analysis method to analyze the single-phase integral effect test facility and obtained the corresponding scaling criteria from the system, component,and process levels.The applicability of the DSS method to the design of integral effect test facilities was evaluated.Similarly, Yoshiura et al.[35] applied this method to the energy distribution component of a thermocline thermal energy storage system in the Dynamic Energy Transport and Integration Laboratory (DETAIL).

In previous studies, simple rectangular loops were typically used to study scaling analysis methods [36, 37].Examples include the primary reactor circuit or core makeup tank [38].To accurately simulate the actual situation and better reflect the coupling effect between the primary and secondary circuits, the reactor can be simplified into a model formed by the coupling of the two circuits.Li et al.[39] designed a full-pressure natural circulation experimental device (FITY) based on pressurized water reactors.A simplified model was established using Relap5 code to verify whether the program could effectively simulate the natural circulation process in the experimental facility.Based on the simplified primary and secondary reactor circuits, Li et al.[40] used the DSS identity transformation method and obtained a set of simplified scaling criteria based on an actual situation.The Relap5 code was used to set the cases for the numerical calculation, and a natural circulation dynamic process corresponding to the scaling cases was obtained.

In this study, the scaling analysis criteria were derived by applying the DSS β- and ω-strain transformations.In addition, a group of simplified β- and ω-strain scaling criteria were obtained for comparison with previous studies.Various cases were set for each scaling criterion by varying the strain parameters.Taking the FITY experimental facilities as a reference, we constructed a model using the Relap5 code to analyze the changes in natural circulation dynamic characteristics with the corresponding variables under each scaling case and subsequently evaluated the differences.

Fig.2 a Scaling number curve based on β- and ω-strain transformations, b Power scaling of the DSS method

2 DSS scaling analysis based on primary and secondary reactor circuits

2.1 Natural circulation model

Natural circulation is a key technology that can be used in passive systems [41].Based on the full-pressure natural circulation experimental facility, a natural circulation model that includes the primary and secondary reactor circuits was established [39, 40].The model is illustrated in Fig.1.The primary circuit is primarily composed of a reactor core simulator, steam generator, pressurizer, reactor coolant pump,pipes, and valves.The secondary circuit primarily consists of the secondary side of the steam generator, a C-type heat exchanger, pressurizer, horizontal pipes, and vertical pipes.In the primary circuit, the core simulator provides heat to the coolant, and the steam generator is used for cold sink simulation to cool the fluid through a heat exchange process with the secondary side.Finally, the single-phase natural circulation is formed in the primary loop.

To simplify the analysis, the Boussinesq approximation hypothesis was adopted for the entire natural circulation loop.In addition, the fluid in the pipe was considered to be one-dimensional, the core heating was regarded as the point heat source, and the heat loss through the pipe was ignored.

2.2 DSS scaling criteria based on strain transformation

As described in previous research, an affine transformation in β-ω coordinate phase plane was applied to the DSS scaling analysis theory, and two strain parametersλAandλBwere used to perform the coordinate transformation [30]:

Five different transformation methods were obtained as follows (Table 1):

These five scaling methods are subsets of the two-parameter affine transformation.β- and ω-strain transformations are essentially unidirectional dilation transformations.The β-strain transformation applies a constant scale factorλAto the β coordinate while leaving the ω coordinate unchanged.Conversely, the ω-strain transformation applies a constant scale factorλBto the ω coordinate while leaving the β coordinate unchanged.

Fig.3 Nodalization of the primary and secondary reactor circuits

In this study, β- and ω-strain transformations were used to derive their respective scaling standards.The treatment of momentum and energy equations has been comprehensively discussed in a previous study [32]; only the key steps are described here.

The momentum integral equation of the loop is as follows:

Fig.4 (Color online) a Normalized mass flow in the primary loop under different cases, b Normalized temperature difference in the primary loop under different cases

The fuel grid spacing and heat pipe diameter for the reactor core and steam generator were considered equal [36, 40].By substituting the strain parametersλAandλB, the following set of scaling criteria can be obtained:

The corresponding scaling standard can be determined by varying the strain parameters.Let the length scalelR= 0.25 and the strain parameters vary between 0.5 and 1.5; the similarity criterion can be obtained.As shown in Fig.2a, the scaling criterion varies with the strain parameters.

The two scaling criteria demonstrate different trends with changes inλ.For β-strain transformation, the scaling ratio of the diameters increases with an increase in the strain numbers.Meanwhile, the geometric dimension of the loop for ω-strain transformation only slightly changes with the strain numbers.Owing to the differences in geometric dimensions, significant differences between the different scaling methods in terms of heat flux exist.The two different methods show similar and relatively small scaling ratios for the powerQrequired by the core simulator assembly, which is conducive to actual situations.

In a previous study, the H2TS method was used to obtain the scaling criteria of natural circulation [39].For comparison, Li et al.[40] used a simplified DSS identity transformation method to analyze the scaling cases.The scaling method was simplified to be consistent with the H2TS method on a geometric scale; further details were presented in [40].Therefore, to better reflect reality and comprehensively evaluate DSS methods, simplified β- and ω-strain criteria were obtained in the same manner:

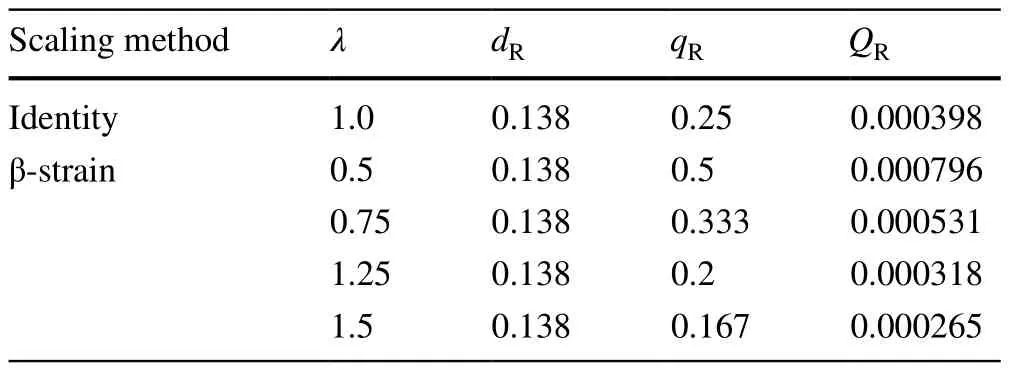
Table 3 Scaling criterion based on the simplified DSS β-strain method

By contrast, the simplified DSS scaling criteria can determine the geometric dimensions of all scaled-down cases after the length ratio is selected.In the model cases,different strain numbers will affect the power ratio.Owing to the difference in the geometric scale of the core simulator, the power scaling based on the simplified DSS method is different from that of the standard one.As shown in Fig.2b, simplified DSS methods require minimal core power in scaled-down cases, which can be beneficial for optimizing the design of thermal experimental facilities.

3 Numerical model

3.1 Node model

The dynamic process of natural circulation in the loops shown in Fig.1 was simulated using the Relap5 code.A node diagram is shown in Fig.3.The reactor core was simulated using pipe structures 102, 104, 106, 108, and 110, which reflect the coolant path in the pressure vessel.Similarly, the pipe components were used to simulate the primary and secondary sides of the steam generator and represent the heat transfer process between the two loops.The heat of the secondary circuit was released by the heat exchanger components represented by pipes 216 and 217.To realize the pressure environment, time-dependent control volumes TDV300 and TDV600 were set for the two loops.

The discrete method was used to solve continuous processes in the Relap5 code.In this case, the number of nodes has a certain impact on the calculation results[42].Therefore, conducting a node sensitivity analysis of the key components is necessary [43].The reactor core and steam generator were analyzed, and their nodes were determined to be 11 and 9, respectively.

3.2 Dynamic cases of natural circulation

The single-phase natural circulation was simulated in the primary loop until the steady state was reached, after which the heating power was adjusted.The loop entered a dynamic process until the next steady state was formed.To compare the flow characteristic parameters for different scaling cases, the dynamic process must be dimensionless.First,it is necessary to evaluate the effect of the power change mode on the dynamic process.Therefore, a series of different dynamic cases are listed in Table 2.

In cases 1, 2 and cases 3, 4, the increase and decrease in power were compared, and different power change modes were set for cases 1, 3 and cases 2, 4.In general, all cases exhibit the same power change rate.The effect of the power change rate was discussed in previous studies [39, 40], concluding that the effect of the power change rate on the normalized curve is not significant when the initial power and final power of several cases are similar.

Figure 4 shows the dynamic process of the normalized mass flow rate and temperature difference between the cold and hot sections in the primary loop in the above cases.Figure 4a shows the mass flow rates of the four cases, with the small figure at the lower-right portion showing the curves of the first three cycles.The horizontal ordinate in the figures representst∗, which is defined ast∗=t∕t0.t0is the time required for the fluid to complete a cycle.The dynamic process of increasing power is slightly faster than that of decreasing power.In all cases, the power change modes have minimal effect on the dynamic process.A similar conclusion can be drawn regarding the normalized dynamic change in the temperature difference between the cold and hot legs of the primary circuit, as shown in Fig.4b.

In summary, Relap5 was used to set such a dynamic process.That is, the power begins to decrease linearly when the single-phase natural circulation reaches the first steady state.Before the circulation reaches the second steady state,the loop presents a dynamic process, and the DSS β- and ω-strain methods are used to set corresponding dynamic scaled cases based on different scaling criteria.

4 Results and discussion

4.1 Results based on the simplified DSS scaling method

First, the simplified methods were used for the simulation by selecting a common length scalelR=0.25.The scaling cases corresponding to the β-strain method are listed in Table 3:

Using this transformation method, each case has the same geometric scale.The selection of the strain numbers is the main difference between the scaling methods.Furthermore,the results show that the β-strain transformation becomes the identity transformation whenλ=1.

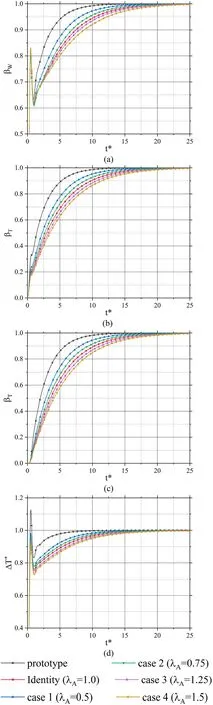
Fig.5 (Color online) Transient curve in the primary loop based on the simplified DSS β-strain method.a Normalized mass flow rate, b Normalized temperature of the hot section, c Normalized temperature of the cold section, d Normalized temperature difference

The single-phase natural circulation in the primary loop is discussed below.Figure 5a shows the dynamic process of the normalized mass flow rate for each scaled-down case.The ordinate was defined asβW=(W1-W)/(W1-W0).In general, there are similar dynamic processes between the prototype and each scaled-down model.The same oscillation process occurred at the beginning of power reduction.For example, the normalized flow rate curve rapidly reached 0.8–0.85 and subsequently decreased by approximately 0.6.This process was completed in the first cycle of power changes.Subsequently, the normalized flow curve gradually increased until the second steady state was reached.Note that the change in the curve from 0 to 1 in the figures represents the degree of the dynamic process.When the curves reach 1, the dynamic process is considered complete.

For all scaled-down cases corresponding to the simplified DSS β-strain method, the process of reaching the steady state is obviously slower than that of the prototype case.Moreover, with an increase in strain number, the speed of reaching the steady state of the scaled-down model is slowed down.When the geometric dimensions of the models are similar,smaller strain numbers correspond to larger power scaling;thus, the steady state can be reached faster.In approximately 20 cycles, the normalized mass flow rate under all scaleddown cases reaches the steady state.

Figures 5b and c show the normalized temperature changes in the hot and cold sections of the model loop in the dynamic process.The temperature at the outlet of the reactor pressure vessel was used to represent the hot section, whereas that at the inlet represents the cold section.The ordinate represents the change in the normalized temperature, which is defined asβT=(T1-T)/(T1-T0) ,whereT0andT1represent the initial and final temperatures,respectively.This reflects the cooling process after the power reduction in each case.Figure 5b shows the change in the normalized temperature at the outlet of the pressure vessel.When the power drops, the temperature curve rapidly reaches approximately 0.35 for the prototype case and gradually reaches a steady state.It is slower for all scaled-down cases than the prototype in the entire cycle, and the initial step change is also less than that of the prototype.Compared with the process of the normalized flow rate, the normalized temperature changes more smoothly with no large oscillations.Furthermore, the relationship between the strain numbers of the dynamic process is similar to that of the normalized flow rate, and all operating cases reach stability after approximately 20 cycles.Figure 5c shows the temperature changes in the cold section at the inlet of the pressure vessel.The difference between the cold and hot sections is mainly reflected in the initial stage.The dynamic process in the cold section becomes significantly slower than that in the hot section.It can be easily explained that the change in core power first acts on the flow characteristics of the fluid at the core outlet and subsequently at the core inlet at the end of the loop.

Fig.6 (Color online) Relative error based on the simplified DSS β-strain method.a Normalized mass flow rate, b Normalized temperature of the hot section, c Normalized temperature of the cold section,d Normalized temperature difference

Figure 5d shows the normalized temperature difference between the hot and cold sections in the dynamic process.As shown on the ordinate, ΔT∗represents the normalized temperature difference, which is calculated asSimilar to the temperature changes, subscripts 0 and 1 represent the temperature differences corresponding to the initial and stable stages,respectively.In the initial stage of the dynamic process, the normalized value also shows an obvious oscillation, and its amplitude is greater than that of the mass flow.This can be observed from the dynamic curve of the normalized temperature of the cold and hot sections.In the initial stage,the temperature change in the cold section has a hysteresis effect, while the fluid temperature at the outlet of the pressure vessel changes immediately.This causes a large distortion in the initial temperature difference.In the following 1 to 2 cycles, the normalized temperature difference reaches a normal value and gradually changes until a steady state is reached.Under the simplified β-strain transformation method, the corresponding scaled-down cases with different strain numbers exhibit similar oscillating processes.The temperature difference reaches the steady state earlier than the normalized flow rate and temperature by approximately 15 cycles.This is because the temperature difference between the hot and cold sections is an important factor causing natural circulation.Therefore, a change in temperature difference causes other flow characteristics to change.

Figure 6 shows the relative errors in the normalized mass flow rate, temperature, and temperature difference between the hot and cold sections.Figure 6a shows the dynamic process of the flow errors over the entire cycle.After the initial oscillation, the deviation begins to increase.In thethird to fourth cycles, the dynamic deviation reaches a maximum value between 10 and 20% and subsequently begins to decline steadily.After the fifth cycle, the dynamic deviation in all cases is less than 15%, the errors tend to zero after 20 cycles.Except for the initial stage, the dynamic deviation in each case also decreases with decreasing strain numbers.The scaled-down case with a strain number of 0.5 has the minimum dynamic deviation with a maximum value of 10%.Figures 6b and c show the normalized temperature dynamic deviations at the outlet and inlet of the reactor core during natural circulation.When the power changes, the temperature errors increase rapidly.In addition, they are larger than the errors in the flow rate.The maximum error for the hot section is between 25 and 50%, whereas that for the cold section is slightly larger – at 30% to 60%.They also decrease rapidly with the number of cycles and finally approach zero.Compared with the mass flow rate, the cycle corresponding to the error peak of the temperature occurs relatively earlier,which can be explained by Figs.5 a–c.There is an obvious oscillation phenomenon during the initial moment, while the normalized parameters of each scaled-down case begin to change steadily at the end of the first cycle.The errors in the flow rate shown in Fig.6a exhibit an irregular oscillation in the first cycle.For the temperature, there is little oscillation in the initial stage of the dynamic process in all cases.Therefore, the curves in Figs.6b and c show the regularity of each case more rapidly.

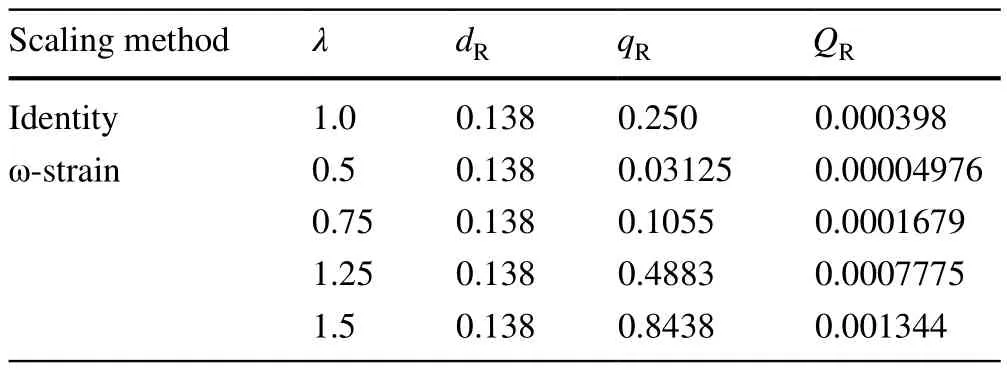
Table 4 Scaling criterion based on the simplified DSS ω-strain method

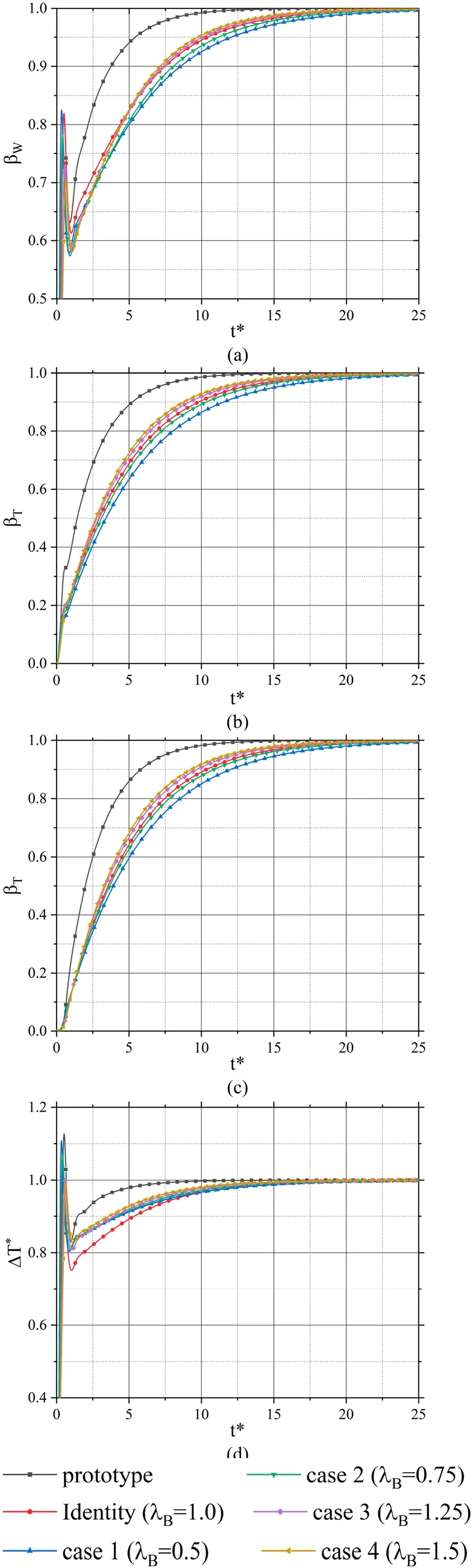
Fig.7 (Color online) Transient curve in the primary loop based on the simplified DSS ω-strain method.a Normalized mass flow rate, b Normalized temperature of the hot section, c Normalized temperature of the cold section, d Normalized temperature difference

Figure 6d shows the dynamic errors in the temperature difference between the cold and hot sections.They have a similar variation range, with a flow rate of 10% to 20%.The errors decrease as the strain numbers increase.A more evident oscillation can be observed at the beginning of the dynamic process, which is equivalent to that shown in Fig.5d.The errors in the temperature difference tend to zero faster than those in the mass flow rate.

Simplified DSS ω- and β-strain methods have the same geometric parameters, which can greatly simplify the setting of scaled-down cases.In addition, the power variation of the ω-strain scaling method is significantly different from that of the β-strain method.The detailed parameters are listed in Table 4.

Fig.8 (Color online) Relative error based on the simplified DSS ω-strain method.a Normalized mass flow rate, b Normalized temperature of the hot section, c Normalized temperature of the cold section,d Normalized temperature difference

The analysis presented herein still focuses on the primary loop.The normalized mass flow rate is shown in Fig.7a.At the beginning of the dynamic process, there is an oscillation similar to that shown in Fig.5a, reaching 0.8 to 0.85.The simplified DSS ω-strain method differs from the β-strain method in the steady ascending stage.As shown in Fig.7a,the ω-strain scaled-down cases during the first five cycles exhibit an almost similar curve of the mass flow rate.The change rate of the flow corresponding to the identity transformation is slightly faster than that of the other cases but remains slower than that of the prototype.After five cycles,the flow rate curves tend to stabilize faster with an increase in strain numbers, which differs from the law corresponding to the β-strain method.This is probably because the scaleddown cases corresponding to the two methods have similar geometric dimensions, whereas the trends of the power changes with strain numbers are opposite (Fig.2).In addition, the rangeability of the normalized mass flow rate for the simplified DSS strain method caused by the change in the strain number is less than that of the β-strain method.

Figures 7 b–d show the normalized temperature and temperature difference.For the temperature, the dynamic process rapidly approaches the steady state with an increase in the strain numbers.However, for the temperature difference between the cold and hot sections, there is a phenomenon different from that of the β-strain method; that is, the normalized value of caseλ=1 (Identity transformation) in the first 10 cycles should be less than that of the other cases where the strain numberλ≠1.Whenλ≠1 , the normalized temperature difference curve gradually approaches that of the prototype with an increase in the strain numbers.

Figures 8 a–c show the errors in the mass flow rate and temperature.After the initial oscillation, the errors decrease with an increase in the strain numbers.For the ω-strain method, the range of dynamic errors between different cases is smaller when the strain numbers change in the same interval.Figure 8d shows the errors in the temperature difference.In the first 10 cycles, the errors of casesλ≠1 are clearly smaller than that of caseλ=1.

4.2 Results based on the standard DSS scaling method

The corresponding criteria for the simplified DSS method were based on the relevant parameters of the experimental facility and the H2TS method.Therefore, the relative scaling of the geometric parameters obtained using the DSS scaling criteria was ignored, which is conducive to the design of experimental facilities.For further comparison, the prototype case based on the standard DSS method was analyzed,and the influence of different strain numbers on the geometric parameters of the scaled-down cases was retained.Each scaled-down case has a corresponding diameter ratio.

For comparison purposes, the length ratiolR= 0.25 was still selected.The scaled-down cases based on the standard DSS β-strain method are summarized in Table 5.

Compared to the simplified method, the standard criterion has different diameter ratios.Larger diameter ratios indicate that the reactor core simulator requires more power.According to the design standard of the FITY facility, a fuel assembly was used to provide the power required by the reactor core simulator [39].The scaled condition obtained using the standard DSS method satisfies the maximum power limit.Therefore, the power scaling criterion obtained by standard DSS transformation is of practical significance.

Figure 9 shows the dynamic curves of the normalized flow, temperature, and temperature difference in the primary loop based on the standard DSS β-strain method.The figures on the right show an enlarged view of the dynamic process curves of the 5th to 10th cycles.In contrast to the results in Fig.5, there are better agreements between the scaleddown model and the prototype in all cases.Compared to the simplified DSS method, the standard DSS method accurately simulates the dynamic process of natural circulation.All cases reach stability around the 15th cycle for flow and temperature, whereas the time is advanced to the 10th cycle for the temperature difference.The time at which all cases reach the steady state is earlier than that of the simplified DSS method.The dynamic processes tend to stabilize faster with a decrease in the strain numbers; however, this trend is not significantly obvious.

Figure 10 shows the corresponding dynamic errors, with Fig.10a illustrating the normalized mass flow rate.Except for the initial numerical oscillation, the deviation in the entire dynamic process is within 5%.Compared to the cases using the simplified scaling method, the errors are significantly reduced, which are more consistent with the prototype case.The dynamic process of the prototype during power reduction is well restored.The temperature errors in the cold and hot sections are also small.After the fifth cycle,the errors in all cases are within 10%, and the errors in the temperature difference can be less than 3%.The reduction in strain numbers further reduces the deviation; however, the reduction amplitude is not significant compared with that of the simplified DSS β-strain transformation method.

Finally, the same method was used to obtain the standard DSS ω-strain transformation scaling criterion (Table 6).

Fig.10 (Color online) Relative error based on the standard DSS β-strain method.a Normalized mass flow rate, b Normalized temperature of hot section, c Normalized temperature of cold section, d Normalized temperature difference

Fig.11 (Color online) a Transient temperature difference in the primary loop based on the standard DSS ω-strain method, b Relative error of the temperature difference in the primary loop based on the standard DSS ω-strain method

Table 5 Scaling criterion based the on standard DSS β-strain method

Table 6 Scaling criterion based on the standard DSS ω-strain method

The DSS ω-strain transformation method was used to perform the same calculations.As shown in Fig.11, the results obtained using the standard DSS ω-strain transformation method for the normalized mass flow rate and temperature behave similarly to those obtained using the standard β-strain transformation method, including the variation trend and error range of the normalized curves.For the normalized temperature difference, the situation is slightly different; that is, the errors decrease with an increase in the strain numbers.However, this phenomenon is not obvious because all the curves of the scaled-down cases are significantly close to those of the prototype case.When the fifth cycle is reached, the deviation in the temperature difference among all the cases becomes less than 3%.Generally, the standard DSS ω-strain transformation method can also accurately analyze the dynamic process of the prototype case.

5 Conclusion

A numerical reactor model coupled with two loops was established based on the FITY experimental facility and analyzed using DSS β- and ω-strain transformation methods.Moreover, taking the H2TS method as a reference, the DSS method was idealized, and a group of simplified DSS β- and ω-strain methods were obtained.The scaled-down cases were set based on the scaling criteria and different strain parameters, and Relap5 codes were used to analyze the dynamic process.The following conclusions were drawn:

1.The simplified DSS β- and ω-strain transformation methods can be used for the scaling analysis of natural circulation.Owing to the different scaling criteria, the reactor core power required for all scaled-down cases corresponding to the simplified DSS method is significantly lower than that of the cases based on the H2TS method.This can simplify the conditions required for scaling experiments.

2.For the simplified DSS β-strain transformation, the speed of reaching the steady state after power change gradually slows down with an increase in strain numbers, whereas it accelerates for the ω-strain method.The speed of reaching stability in all scaled-down cases is slower than that of the prototype.When the variation range of strain numbers is similar, the variation ranges of the dynamic errors of the simplified ω-strain method are smaller than those of the β-strain method.

3.According to standard DSS methods, different scaleddown cases correspond to different geometric scaling criteria.The pipe diameters in the scaled-down cases changes with strain number.Because of the different scaling criteria, the core power required by the scaled model is greater than that required by the simplified DSS method.The cases based on the standard DSS method accurately reflect that of the prototype.The deviation in various dynamic parameters is significantly small.

In future work, the research will focus on different length ratios and two-phase natural circulation, and relevant experiments will be conducted based on the thermal–hydraulic bench.Thus, the theoretical research on dynamic scaling analysis methods can be enhanced and improved.

Author contributionsAll authors contributed to the study conception and design.Material preparation, data collection and analysis were performed by Jia-Ning Xu, Xiang-Bin Li.The first draft of the manuscript was written by Jia-Ning Xu and all authors commented on previous versions of the manuscript.All authors read and approved the final manuscript.

Data AvailabilityThe data that support the findings of this study are openly available in Science Data Bank at https:// www.doi.org/ 10.57760/ scien cedb.j00186.00172 and https:// cstr.cn/ 31253.11.scien cedb.j00186.00172.

Declarations

Conflict of interestThe authors declare that they have no competing interests.