考虑两端实际约束的隧道施工诱发邻近桩基响应解析解

2023-10-13孙影杰施成华王祖贤张轩煜郑晓悦

中南大学学报（自然科学版） 2023年8期

孙影杰，施成华，王祖贤，张轩煜，郑晓悦

(中南大学土木工程学院，湖南长沙，410075)

城市地下隧道穿越建筑物密集区域时，将不可避免地对邻近既有桩基产生影响。隧道施工扰动周围土体，进而导致邻近桩基产生附加变形和内力，严重时可能影响上部结构稳定，危及上部结构安全。因此，如何较准确地预测桩基响应对于指导现场施工具有重要意义。隧道施工对邻近桩基的影响的实质是隧道-土体-桩基之间相互作用，目前研究手段主要有现场实测[1-3]、物理模型试验[4-6]、数值模拟[7-9]和理论解析[10-12]。相较于前几种方法，理论解析物理意义明确、计算方便快捷，是解决该问题的有效手段之一[13-14]。当前，基于解析法研究隧道施工诱发邻近桩基响应问题时，主要采用两阶段分析法[11,15-16]，即首先计算隧道施工后桩位处土体自由场位移，然后将土体位移以附加荷载的形式作用在桩基上，并根据地基梁理论建立桩基变形的控制微分方程，继而基于边界条件求得控制方程的严格解析解或半解析解。但该问题的控制方程往往为四阶非齐次微分方程，当荷载形式较复杂时，在数学上要得到其严格解析解存在一定的困难。相对而言，有限差分法可以避免高阶微分方程在数学求解上的困难，且对复杂荷载形式和层状地基均具有良好的适用性，目前被广泛应用于桩基响应问题的研究[17-19]。值得注意的是，为便于差分方程的求解，既有研究往往将桩基视为桩顶无约束、桩端自由的有限长梁[10-11,13,16,20]。将摩擦桩的桩端视为自由边界是可行的，但对于端承桩特别是嵌岩桩，岩层对桩端的约束不可忽略。另外，工程中除部分隔离桩外，桩顶通常嵌入承台或筏板基础，将其简化为自由边界与实际情况不符。求解微分方程实质上是求解处理边值问题，边界条件是求解微分方程的决定性因素。由此可见，考虑桩基两端的实际约束状态是很有必要的。

现阶段，桩-土相互作用问题解析模型的构建仍然依赖于弹性地基梁理论，即将桩基视为弹性地基中的有限长梁，由此结合不同的地基模型和梁理论即可建立多种解析计算模型。目前，常用的地基模型中Winkler地基模型未考虑地基弹簧间的剪切效应，尽管Pasternak 地基模型弥补了这一不足，但采用Pasternak 地基模型计算时土体剪切参数主要凭借经验确定，既有研究成果中参数取值差别较大。相较于前2种地基模型，Vlasov地基模型能够反映土体剪切特性，且参数取值更具理论依据[13]。与Euler-Bernoulli梁相比，Timoshenko梁能同时反映弯曲和剪切特性，故将桩基等效为Timoshenko梁更具广义性。

隧道近接施工诱发邻近桩基横向附加响应，为此，在既有研究的基础上，采用两阶段法并考虑桩基两端的实际约束状态，将桩基视作Vlasov地基中端部为任意弹性约束的Timoshenko 梁，建立桩基横向变形的广义解析计算模型，基于有限差分法获得桩基附加变形和内力的半解析解。

1 计算模型

隧道-土体-桩基的相互作用模型如图1(a)所示，其中，Hi为第i层土层厚度，ki和ti分别为第i层土层的地基反力系数和荷载传递率，R和H分别为隧道半径和轴线埋深，Lp和Dp分别为桩基长度和直径，y0为隧道轴线与桩基水平间距。桩基在附加荷载作用下产生附加变形和内力。考虑桩顶承台(或筏板基础)及桩端岩土体对桩基两端的实际约束，将桩基视为两端受水平弹簧(刚度分别为Kt0和Ktn)和转动弹簧(刚度分别为Kθ0和Kθn)约束的弹性地基梁，如图1(b)所示，其中q(z)为桩位处土体横向位移产生的附加荷载，p(z)为地基反力。

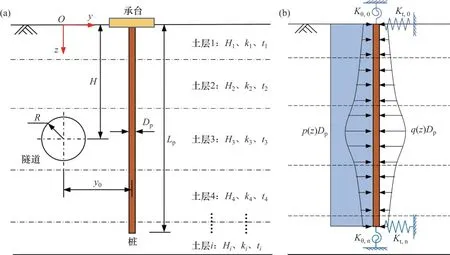
图1 隧道-土体-桩基简化计算模型Fig.1 Simplified calculation model of tunnel-soil-pile

2 理论推导

2.1 基本假定

本文仅分析隧道施工完成后邻近桩基的变形和内力，不考虑隧道施工过程对桩基响应的影响。首先进行如下假定：

1) 桩基等效为可同时反映弯曲和剪切特性的Timoshenko梁；

2) 采用Vlasov 地基模型描述桩-土相互作用关系；

3) 忽略桩基和土体之间的摩擦且两者变形协调。

2.2 解析模型的控制方程

对于Vlasov 地基，地基中任意一点的地基反力p与该点位移w的关系为[21]

式中：k和t分别为地基反力系数和荷载传递率[22]；Es和μs分别为土体弹性模量和泊松比；He为地基弹性层厚度，LIANG 等[23-24]建议其取桩径的2.5 倍；h=h(z)，为描述位移沿竖向变化的函数，一般可按线性或指数函数的形式取值，为便于计算，本文采用如下线性函数形式表示：

式中：z为计算点埋深。

根据Timoshenko 梁的本构方程[25]，桩基变形和内力的关系为

式中：M、Q、w和φ分别为桩基弯矩、剪力、挠度和截面转角；EI和κGA分别表示截面抗弯刚度和剪切刚度，E为弹性模量；I为截面惯性矩；G为剪切模量；A为截面面积；κ为剪切修正系数，对于圆形截面，取κ=0.89。

图2所示为桩微段单元受力示意图，由静力平衡和弯矩平衡可得：

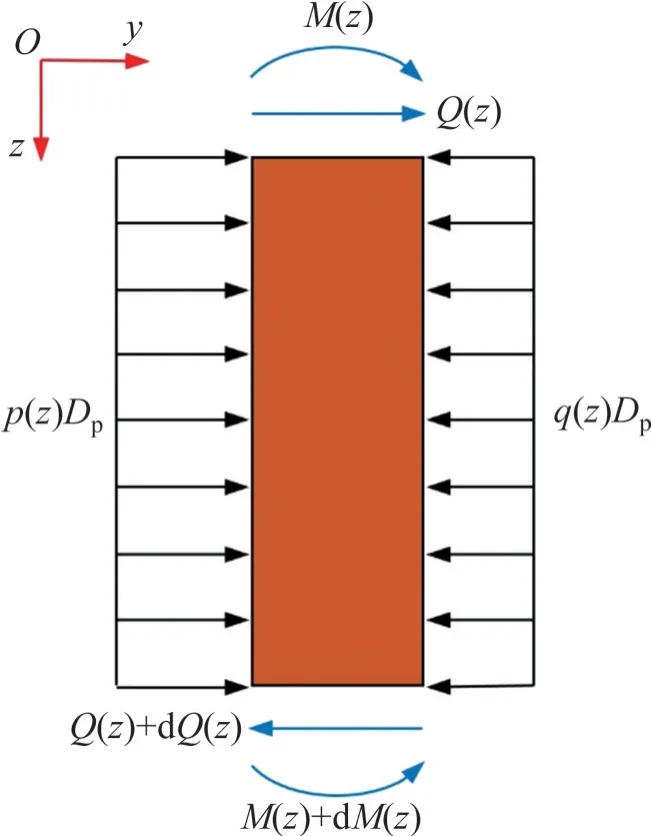
图2 桩微段受力示意图Fig. 2 Diagram of forces analysis of pile element

忽略二次高阶项(dz)2，将式(1)和(4)代入式(5)和(6)，建立桩基横向变形w和转角φ的平衡微分方程：

对式(7)和(8)进行解耦，令C=κGA，D=EI，K=kDp，T=2tDp，化简后可得桩基横向变形的控制微分方程为

其中，q(z)可按下式计算确定：

式中：u(z)为隧道开挖引起的桩位处土体自由场横向变形，可采用LOGANATHAN 等[26]提出的土体位移解析式求解。隧道开挖后地层中任意一点的横向变形u为

式中：ε为等效地层损失率；y为计算点至隧道轴线水平距离；z为计算点埋深。

2.3 控制方程的求解

式(9)为四阶非线性微分方程，为进一步考虑土体层状特性，借助有限差分法展开求解。图3所示为桩基离散示意图。由图3可知：沿轴向将桩基离散成n个长为l的梁单元，为便于构建差分方程，桩基两端各增加2 个虚节点，编号分别为-2、-1、n+1 和n+2。采用中心差分原理构造差分方程，得到控制微分方程式(9)的有限差分表达式为

图3 桩基离散示意图Fig. 3 Discrete diagram of pile

式中：wi和qi表示节点i处桩基横向变形和附加荷载；l为梁单元长度。

求解式(12)即可得到隧道开挖引起的邻近桩基横向变形。结合式(4)、(7)和(8)可得桩基横截面转角φ、弯矩M和剪力Q，并将其写成如下差分形式，为

由式(12)可得n+1个独立方程，但未知量有n+5 个，需根据桩基两端内力边界条件补充4 个独立方程。为此，以桩顶为例，取节点i=0～1之间的单元作为分析对象。图4所示为节点0～1隔离体微段受力分析图。由图4 可知：i=0 节点为柔性支座，i=1 节点为梁截断点；qm为节点i=0～1 之间的附加荷载，计算时可取两节点处附加荷载的平均值。

图4 节点0～1隔离体微段受力分析图Fig. 4 Diagram for force analysis of the micro-section of isolator at nodes 0-1

由力法方程可得节点i=0 处桩基弯矩M0和剪力Q0：

式中：δ11、ΔP11、ΔP21分别为单位荷载、地基反力pDp、附加荷载qDp单独作用时在节点i=0 处产生的位移；δ21、ΔP12、ΔP22分别为单位荷载、地基反力pDp、附加荷载qDp单独作用时在节点i=1处产生的位移，且

结合式(14)和(16)，可得虚节点位移w-1和w-2：

式中：

将式(12)表示为矩阵形式：

式中：

2.4 算例验证一

XU 等[27]采用边界元程序GEPAN 分析了隧道近接施工后地层损失率ε对既有桩基的影响，得到ε分别为1.0%、2.5%和5.0%时桩基横向变形和弯矩的数值解。隧道与单桩相对位置关系及桩基响应计算参数如图5所示。不考虑土体分层特性和竖向荷载作用，假设均质土体弹性模量Es=24 MPa，泊松比μs=0.5，隧道半径R=3 m，轴线埋深H=20 m；桩基弹性模量Ep=30 GPa，桩长Lp=25 m，桩径Dp=0.5 m，隧道轴线与桩基水平间距y0=4.5 m。假定桩基两端为自由端，计算时取Kt0=Ktn=1×10-9kN/m，Kθ0=Kθn=1×10-9kN·m/rad，模拟桩顶和桩端不受任何约束。

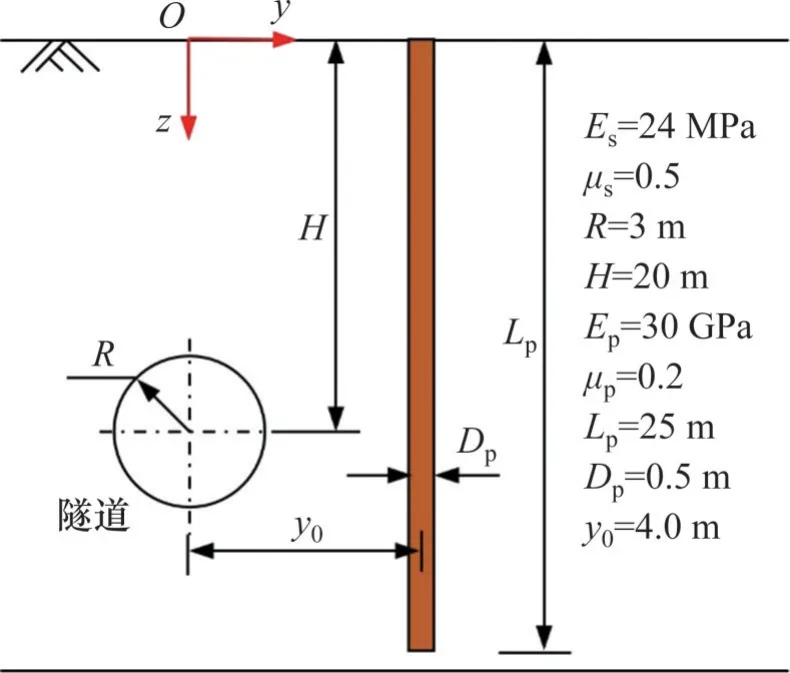
图5 隧道与单桩相对位置及均质土计算参数Fig. 5 Relative position and calculation parameters of tunnel and single pile of homogeneous soil

图6所示为均质土桩身横向变形和弯矩对比曲线。由图6 可见：当地层损失率为1.0%、2.5%和5.0%时，本文解析解与数值解整体变化趋势基本一致，桩身最大横向变形和弯矩发生在隧道中心线附近，说明本文方法对不同程度的地层损失均具有一定的可靠性。本文方法计算所得桩身横向变形与数值解非常接近，但略微高估了桩身弯矩；当地层损失率为5.0%时，本文方法和边界元法计算所得桩身最大弯矩分别为310 kN·m 和290 kN·m，相对误差约为6.9%。

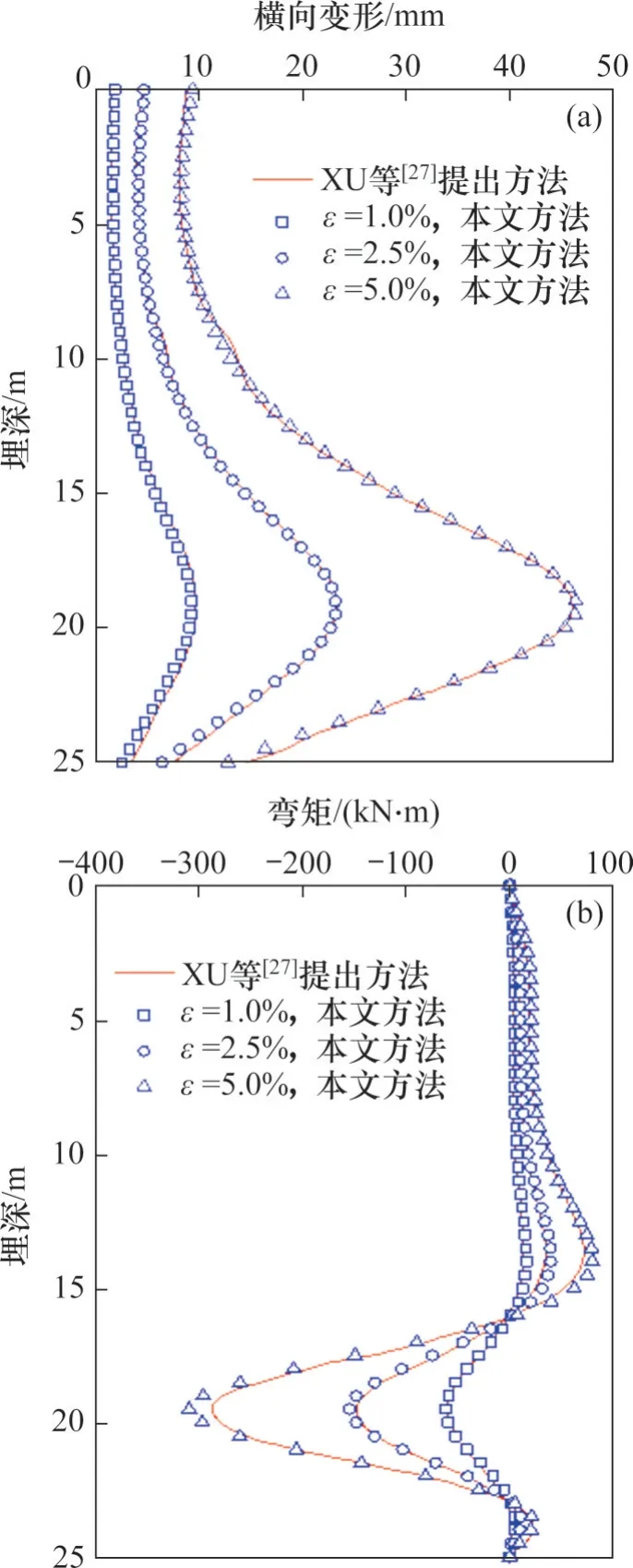
图6 均质土桩身横向变形和弯矩对比曲线Fig. 6 Comparison curves of transverse deformation and bending moment of pile of homogeneous soil

2.5 算例验证二

MU 等[28]采用位移控制有限元法DCFEM 探究了隧道施工对邻近桩基变形和内力的影响。考虑地基土体分层特性，桩基埋深范围内简化为两层土体，上层土厚为10 m，其余计算参数见图7。

图7 隧道与单桩相对位置及成层土计算参数Fig. 7 Relative position and calculation parameters of tunnel and single pile of layered soil

本文方法计算所得桩身横向变形和弯矩与MU等[28]的有限元数值解的对比见图8。由图8 可见：本文方法与MU等[28]的计算结果整体变化趋势基本一致，说明本文方法可较准确地预测层状地基中既有桩基对邻近隧道施工的响应。图8中，在埋深10 m 处，桩身弯矩发生轻微跳跃，这是由于该位置处于土层交界面，土体弹性模量从12 MPa 突变至24 MPa。

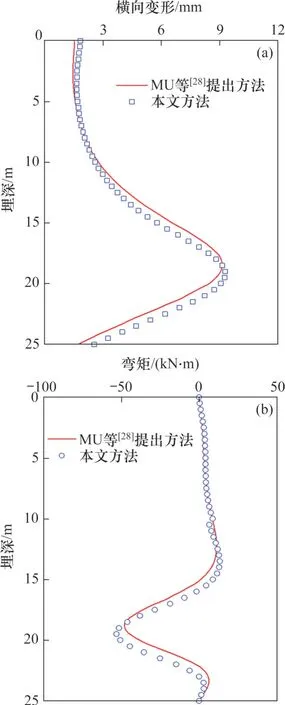
图8 成层土桩身横向变形和弯矩对比曲线Fig. 8 Comparison curves of ransverse deformation and bending moment curves of pile of layered soil

3 桩顶及桩端约束对桩基响应的影响

采用2.4节中算例，针对ε=2.5%这种工况，探究桩基两端约束条件对其变形和内力的影响规律。当桩基两端自由(Kt0=Ktn=1×10-9kN/m，Kθ0=Kθn=1×10-9kN·m/rad)和固定(Kt0=Ktn=1×109kN/m，Kθ0=Kθn=1×109kN·m/rad)时，桩身横向变形和内力曲线如图9 所示。从图9 可见：与桩基两端自由相比，当桩基两端固定时，桩身横向变形和弯矩在桩基两端附近存在显著差异，尤其是桩顶和桩端位置处。由计算结果可知，当桩基两端自由时，桩顶和桩端横向变形分别为w0free=4.68 mm 和wnfree=6.40 mm；当桩基两端固定时，桩顶和桩端弯矩分别为M0fix=302.9 kN·m和Mnfix=824.8 kN·m，桩顶和桩端剪力分别为Q0fix=411.7 kN 和Qnfix=-826.0 kN。由此可见，在实际工程中，将桩基两端简化为自由边界可能会带来较大计算误差，需根据现场情况合理确定桩顶和桩端约束状态。

图9 桩身横向变形和内力曲线Fig. 9 Transverse deformation and internal force curves of pile

3.1 桩基两端实际约束状态的简化计算方法

对于低桩承台基础，桩顶水平位移约束主要来源于两部分，即承台侧面土体弹性抗力和承台底面摩阻力。桩顶水平弹簧刚度Kt0可按下式简化计算：

式中：S侧为埋入土体中的承台侧面积；μ为承台底与地基土间的摩擦因数，可参考规范文献[29]取值；Pc为承台底土体承受的竖向荷载；n为桩的数量；Cz为地基水平抗力系数，可按Cz=mz计算确定，其中水平抗力系数的比例系数m据文献[29-30]综合取值。

桩顶转动弹簧刚度Kθ0可按下式近似计算：

式中：EI为承台的抗弯刚度。

桩端水平弹簧刚度Ktn和转动弹簧刚度Kθn可按下式简化计算：

式中：A为基桩底面积；I为桩端截面惯性矩；Cx和Cφ分别为地基抗剪和抗弯刚度系数。《工程地质手册》[31]给出了Cx、Cφ与地基抗压刚度系数Cz的关系，Cx=0.7Cz，C=2.15Cz，其中Cz可由现场试验确定或根据天然地基的承载力近似取值。

3.2 桩顶实际约束对其变形和内力的影响

桩顶横向变形、弯矩和剪力随水平弹簧刚度Kt0和转动弹簧刚度Kθ0的变化曲面见图10。假设任意边界条件下桩顶横向变形、弯矩和剪力分别为w0、M0和Q0，对桩顶横向变形和内力进行归一化处理，得到桩顶横向变形比w0/w0free、弯矩比M0/M0fix和剪力比Q0/Q0fix。

图10 桩顶横向变形和内力曲面Fig.10 Transverse deformation and internal force surfaces of pile top

由图10(a)可知：相较于水平弹簧刚度Kt0，转动弹簧刚度Kθ0对桩顶横向变形的影响较小；当Kt0=1 kN/m 时，随着Kθ0增大，桩顶横向变形从w0free减小至0.96w0free；当Kθ0一定时，桩顶横向变形随Kt0的增大而减小，且当1×103103kN·m/rad 且Kt0>1×103kN/m 时，桩顶弯矩随Kt0和Kθ0的增大而增大，且Kt0和Kθ0越大，桩顶弯矩增幅越明显。由图10(c)可知：当Kt0<1×103kN/m 时，桩顶剪力很小，几乎不随Kθ0的变化而变化；当Kt0>1×103kN/m 时，桩顶剪力随Kθ0的增大而增大，且当Kt0>1×106kN/m时，桩顶剪力随Kθ0显著变化；当Kt0为1×109kN/m 时，随着Kθ0增大，桩顶剪力从0.53Q0fix增大至Q0fix；当Kθ0一定时，桩顶剪力随Kt0的增大而增大，且Kθ0越大，桩顶剪力增幅越明显。

综上可知：当Kt0<1×103kN/m 且Kθ0<1×103kN·m/rad时，桩顶横向变形为w0free，桩顶弯矩和剪力几乎为0，近似于桩顶自由；当Kt0>1×107kN/m 且Kθ0>1×107kN·m/rad 时，桩顶几乎不发生横向变形，且桩顶弯矩和剪力均达到最大值M0fix和Q0fix，可按桩顶固定简化计算。

3.3 桩端实际约束对其变形和内力的影响

采用3.1节中桩端水平弹簧刚度和转动刚度的计算方法计算本文算例，所得桩端转动刚度约为水平弹簧刚度的1/18，在此基础上，研究桩端约束条件对其变形和内力的影响规律。假设任意边界条件下桩端横向变形、弯矩和剪力分别为wn、Mn和Qn，对桩端横向变形和内力归一化处理，得到横向变形比wn/wnfree、弯矩比Mn/Mnfix和剪力比Qn/Qnfix。

桩端横向变形和内力随桩端水平弹簧刚度的变化如图11 所示。由图11 可知：当Ktn<1×103kN/m时，桩端近似于自由端；当1×103≤Ktn≤1×106kN/m时，桩端横向变形随弹簧刚度的增大而减小，当Ktn=1×106kN/m 时，横向变形减小至0.043wnfree；当Ktn≥1×104kN/m时，桩端剪力随弹簧刚度增大而增大；当Ktn≥1×105kN/m时，桩端弯矩随弹簧刚度的增大而增大，当Ktn=1×107kN/m时，弯矩和剪力分别增大至0.85Mnfix和0.90Qnfix；当Ktn达到1×108kN/m 时，桩端横向变形和内力不再变化，桩端近似为固定端。