基于改进蒙特卡洛树搜索的无人机目标分配与突防决策方法
2023-10-13熊韫文魏才盛许丹周亮薛晓鹏
熊韫文,魏才盛,许丹,周亮,薛晓鹏
(1. 中南大学 自动化学院,湖南 长沙,410083;2. 中南大学 空天智能控制研究中心,湖南 长沙,410083;3. 国防科技大学 系统工程学院,湖南 长沙,410073;4. 航天科工集团智能科技研究院有限公司,北京,100144)
无人机协同作战表现出独特的飞行性能和打击效果,被广泛应用于战场侦察、防空压制、纵深扣击等军事任务中。同时,反无人机技术也不断发展,越来越智能化,且具有成本低、拦截效率高、动态适应力强等特点[1],这对多无人机协同作战任务规划技术提出了新挑战。目前,国内外学者针对多无人机任务规划问题展开了大量研究,这些研究大多将任务规划中的各阶段问题进行分开求解,未考虑问题间的耦合关系。WANG等[2]针对异构多无人机系统任务分配问题,在考虑任务时间、收益、损耗等优化目标的基础上,提出了一种多目标量子粒子群算法对问题进行求解。HU等[3]针对严重不确定性条件下的空对地攻击任务,提出了一种无人机鲁棒决策集成框架。CHEN等[4]为解决不同状态下无人机构型变换过程中的实时航迹规划问题,提出了一种融合Dubins 轨迹与粒子群优化算法的方法。近年来,一些研究者针对任务规划问题间的耦合关系进行了研究,针对问题间的耦合性提出了一些统一求解的方法,王然然等[5]基于分布式合同网拍卖和A*算法,在目标分配阶段对航路进行初规划,确定最佳任务执行次序。赵明等[6]针对三维环境下无人机集群目标分配问题,对各种目标分配模型统一建模,设计了一致的模型处理方法,能够有效解决三维环境下不同模型的多机多目标分配问题。这些研究将目标分配与航迹规划进行统一建模,为并行解决目标分配与突防决策问题提供了思路。对于目标分配与突防决策问题,前者基于后者的结果选择最优的目标,后者基于前者的目标信息对突防动作进行决策,只有两者相互耦合,将其统一建模并求解才能凸显无人机作战任务规划的合理性。
目标分配和突防决策本质上是组合优化问题,该类问题一般是在一个有限的离散集合中找到某一组合,直观上可用暴力穷举的方式得到最优解,但随着问题复杂程度加大,计算复杂度呈指数级增加[7]。为提升规划问题求解的时效性,一些研究者提出了其他方法进行求解。例如,王雅琳等[8]针对交通运输领域中的装卸货任务分配问题,提出了一种用于求解该类问题的离散微粒群算法。苏丽颖等[9]针对信息量大、数据处理复杂的多机器人任务分配问题,对该问题进行形式化描述,并提出了一种基于组合拍卖法的分布式建模方法。邹子缘等[10]针对空间飞行器集群对抗中的多对多目标分配问题,提出了基于深度优先搜索生成目标分配指导表的方法。朱建文等[11]针对导弹集群多目标分配问题,建立了导弹综合攻击性能评估标准,并利用Q 学习算法对导弹选择以及分配形式进行智能决策。
然而,针对目标分配和突防决策问题,两者的优化函数、决策变量和约束各不相同,上述方法不能对该问题进行同时求解。为此,本文作者在充分厘清目标分配与突防决策优化函数内在联系的基础上,对无人机协同任务规划问题进行描述和建模。为了能够同时实现对目标分配和突防决策问题求解,在多种约束下分阶段构建协同任务规划问题的状态空间、动作空间与奖励函数,并提出一种改进的蒙特卡洛树搜索(Monte Carlo tree search, MCTS)强化学习算法,在求解最大收益目标函数下,获得对多无人机目标分配和突防决策问题的优化求解。
1 目标分配与突防决策统一建模
以多无人机协同攻击地面静态目标群为背景,考虑地面防御部署,建立多无人机目标分配和突防机动决策统一目标函数。
1.1 无人机攻击优势度和目标威胁度
在无人机群协同攻击过程中,为了有效攻击目标,无人机群通常需要考虑攻击角度和协同攻击时间[12],针对上述因素分别建立攻击优势度评估函数。
无人机在攻击目标时需满足终端入射角约束。假设无人机初始航向角为γ0,攻击目标的终端入射角为γf。在侧向平面中,无人机控制的目标主要是消除航向角和终端入射角之间的误差,所以,当初始航向角和终端入射角之间的误差越小时,控制也就越容易实现,这意味着攻击优势度越大。攻击角度优势度AUγ为
协同攻击时间也是影响无人机群攻击效率的重要因素,单架无人机攻击目标的时间与协同攻击时间相差太大将影响打击任务完成质量,因此,优势度评估需考虑时间。假设T0为综合考虑无人机群机动能力而确定的协同攻击时间,t为单架无人机攻击时间,则攻击时间优势度AUt为
同时,以较直观的目标战略价值作为目标威胁评估的标准,多个目标具有不同的战略价值,目标的战略价值越大,则受威胁程度越大。假设共有NTar个目标,νTar,j为第j个目标的战略价值,目标的威胁度ATar为
根据上述攻击角度优势度、攻击时间优势度和目标威胁度,可建立综合优势度模型A为
式中:λγ、λt和λν分别为攻击角度优势度权重因子、攻击时间优势度权重因子以及目标威胁度权重因子,λγ+λt+λν=1。可针对不同目标分配任务中的不同侧重点,人为地选择这3个权重因子。
1.2 无人机目标分配优化函数建模
假设在无人机集群协同作战过程中,共有NU架无人机和NTar个目标,基于上述优势度评估函数,建立无人机对目标的优势度矩阵Aij,该矩阵中第i(i=1,2,…,NU)行、第j(j=1,2,…,NTar)列的值表示无人机i对目标j的综合优势度。同样,为了直观地表示目标决策结果,建立无人机对目标的目标分配矩阵Xij,该矩阵中元素为1表示将无人机i分配给目标j,矩阵元素为0 则代表无人机i不分配给目标j。为了得到最优的目标分配矩阵,建立以下目标分配优化函数:
式中:Jdis,i为无人机i的目标分配优化函数。在目标分配过程中,每架无人机只能被分配给1 个目标,并且需要保证每个目标至少分配1 架无人机,因此,可建立以下约束模型:
1.3 无人机突防问题描述
在多无人机突防过程中,假想敌通常是以目标为核心,建立纵深、多道反制装备部署[13]。根据多无人机突防战术特征,按照纵深梯次部署顺序主要考虑以下防空杀伤因素。
1) 侦察与监视系统。该系统主要包括探测雷达和防空预警指挥系统,将对无人机群进行定位,并将信息提供给队属防空兵器、中程地空导弹、远程地空导弹等杀伤类防空系统。
2) 队属防空兵器系统。该系统部署在战斗接触线前,由近程低空导弹系统构成,主要用来防御低空目标。
3) 中程地空导弹系统。该系统部署在队属防空兵器后,其拦截高度更高和拦截速度更快,能够建立密集杀伤区。
4) 远程地空导弹系统。该系统部署于中程地空导弹系统,主要用于掩护目标。
目前,各国都十分重视反无人机群技术的开发和使用,设计了反无人机系统与指控系统用于探测和对抗无人机[14-15]。本文分别用探测概率和被击毁概率表征防空系统对无人机的探测能力和拦截能力,如表1所示。

表1 各防空系统探测或击毁概率Table 1 Detection or destruction probability of defense system
无人机突防行为主要表现在对上述纵深梯次防空系统区域的探测或攻击作出隐身或机动动作,以降低被探测概率或被摧毁概率。假设无人机主要拥有5种突防动作,包括隐身、转弯机动、跃升机动、俯冲机动和蛇形机动,其中,转弯机动、跃升机动、俯冲机动和蛇形机动统称为机动动作。文献[16-21]通过建立无人战斗机飞行动力学和导弹导引飞行控制模型,研究了无人战斗机在导弹威胁情况下各种机动动作的逃逸概率。基于文献[16-21],建立无人机突防动作对各防空杀伤因素的突防概率表,分别如表2、表3所示。

表2 突防动作对侦查与监视系统的突防概率Table 2 Probability of penetration action to investigation and monitoring system
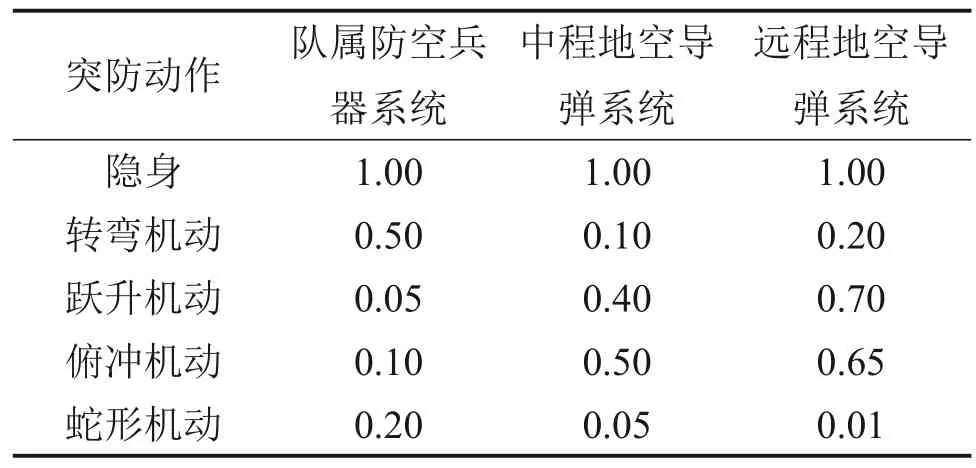
表3 突防动作对防空杀伤系统的突防概率Table 3 Probability of penetration action to defense system
1.4 无人机突防决策优化函数建模
无人机突防动作决策是对目标优化分配后的无人机进行下一步突防动作决策优化。首先,假设不同目标部署的各防空区域数量不同,即第j个目标共有Nd,j个防空区域,包含Ndr,j个侦察与监视系统、Ndsm,j个队属防空兵器系统、Ndmm,j个中程地空导弹系统以及Ndlm,j个远程地空导弹系统,无人机共有NA个突防动作供选择,经过每一个防空区域选择一个动作进行突防。其次,以突防概率表2、表3为基础,建立突防概率矩阵Pmk,该矩阵表示执行突防动作m(m=1,2,…,NA) 在第k(k=1,2,…,Nd,j)个防空系统区域里的突防概率。最后,通过优化获得无人机突防动作矩阵Mkm。若无人机在第k个防空系统区域里选择突防动作m,则矩阵元素为1,否则为0。可建立如下无人机突防动作决策优化函数:
式中:Jpene,i为无人机i的突防动作决策优化函数,其含义是无人机若被对空侦查与被监视系统探测到,则需要对各防空系统进行突防,否则可以对目标直接进行攻击,因此,该函数由两部分概率组成。同时,根据无人机的物理特性,在无人机突防过程中,对所有突防动作和机动动作的选择次数进行约束,即每种动作选择不超过b1次以及机动动作选择不超过b2次。突防动作决策问题约束为
1.5 无人机目标分配与突防决策统一目标函数建模
无人机集群目标分配问题和突防动作决策问题相互耦合,目标分配基于突防动作决策优化得出的概率进行最优化匹配,突防动作决策则是在目标分配的基础上选择最优突防动作序列。两者在任务模型上是一个问题的2个阶段,前者为后者提供任务需求关系,后者实现前者的期望目标[6]。上述2个问题本质上是一个组合优化问题,即在离散决策空间对决策变量进行最优选择,其决策变量的选取与强化学习的动作选择十分契合[22],因此,利用线性加权法将两者的优化函数转化成一个单目标优化问题,并利用蒙特卡洛树搜索算法对该多阶段决策问题进行统一求解。
首先,对于第i架无人机,基于式(5)中的目标分配优化函数和式(7)中的突防动作优化函数,建立统一目标函数:
式中:ζ1、ζ2为用于平衡目标分配和突防决策之间的参数。基于上述单无人机统一目标函数,利用线性加权法将多目标优化问题转化为单目标优化问题,得到协同任务规划统一目标函数:
式中:ρ1、ρ2、…、ρNU为权重因子,可人为地根据任务目标进行选择,并且ρ1+ρ2+…+ρNU=1。最后,统一目标函数的约束由式(6)和式(8)组合而成:
2 基于改进MCTS算法的问题求解
MCTS 是强化学习算法中的一种,其性能在AlphaGo智能机器人上得到验证[23]。MCTS在给定域中通过对决策变量进行随机采样来寻找最优解,其搜索过程呈现出树的特征,即树的边代表决策变量的选取状态,以节点的形式存在树中[24]。
该算法使智能体不断地试错,并根据人为设定的奖励函数指导学习出一个最优策略。该策略的输入为状态,输出为动作,最终得到一个最优的动作序列。算法主要包含选择、扩展、模拟和反馈共4步[25]。对于当前状态节点,算法根据选择策略选择动作;执行这个动作;获得新状态,若这个状态已经在树上则评估这个状态,否则就将新节点插到树上,并从这个状态出发运行随机模拟策略,直到终止状态;最后,通过反向回溯来更新路径上每个状态的回报值。
为了平衡探索和利用之间的关系,将UCB(upper confidence bound)方法与树搜索策略相结合,形成了UCT(upper confidence bound apply to tree)算法[26]。在UCT算法中,N(v)为该节点的访问次数,Q(v)为经过该状态节点所获得的回报。UCT 算法的选择策略公式如下:
式中:vfather为节点v的父节点;Cp为常量,用于权衡探索和利用的取向关系。在搜索达到最终状态节点时,将得到的奖励总和通过以下公式对路径上所有节点进行回溯更新:
式中:ΔQ为1轮模拟得到的回报。
针对多无人机目标分配和突防动作决策问题,其求解过程是从一个可数有限的0-1排列组合中寻找一组排列,这类组合优化问题旨在找到极值点。然而,UCT 算法优先选择具有最高平均回报的分支,因此,式(12)使用均值选择动作的策略不适用于组合优化问题的求解。同时,文献[27]指出UCT算法中的均值搜索策略需要大量迭代才能优化出最优动作序列。
2.1 强化学习建模
首先,针对本文所需求解的问题用马尔科夫决策过程(Markov decision processes, MDP)进行建模。
状态是智能体与环境信息的表征,在迭代过程中,智能体根据状态来选择动作,所以,状态的选取对训练结果有十分重要的影响。本文所求解的问题由目标分配和突防两阶段组成,目标分配为突防的前提阶段,只有在无人机选择完目标后才能根据目标所部署的纵深梯次防空系统依次进行突防。为了解决该问题,将目标分配当作初始状态,并与后续防空系统状态相结合进行统一状态空间建模。对第j个目标,其状态空间可建立为
其中:Sdis为无人机处于目标分配阶段的状态变量;Sr为无人机在突防阶段经过对空侦察与监视系统的状态变量;Ssm1,Ssm2,…为无人机在突防阶段经过队属防空兵器系统的状态变量;Smm1,Smm2,…为无人机在突防阶段经过中程地空导弹系统的状态变量;Slm1,Slm2,…为无人机在突防阶段经过远程地空导弹系统的状态变量。状态间转移是离散和确定的,可根据目标部署的防空系统态势信息建立。综合所有目标的状态空间,总状态空间可表示为
无人机在目标分配与突防过程中的状态存在差异性,其动作也不同。在目标分配阶段,动作为目标选择,无人机只能选择1个目标,其结果可用离散化的向量表示,即adis=[0 1 0 … 0]。若存在NTar个目标,则目标分配阶段有NTar个动作可供选择。在突防阶段,动作为5种突防动作,无人机在任意一个突防阶段仅选择1个突防动作。将5种突防动作用向量表示,向量中的元素依次代表隐身、转弯机动、跃升机动、俯冲机动和蛇形机动,如apene=[1 0 0 0 0]表示无人机选择了隐身动作。基于上述分析,无人机动作表示为
奖励函数是强化学习中最核心的部分,它指导智能体进行学习。针对本问题,只有智能体到达最终状态即决策出完整的目标分配矩阵和突防动作矩阵后,才能根据统一目标函数对上述决策结果进行评价,因此,针对该问题只设计终局奖励。基于统一目标函数和约束,设计联合奖励函数如下:
式中:当目标分配矩阵X和突防动作矩阵M1,…,MNU所表征的决策变量不满足约束时,给予惩罚-0.2;否则给予奖励,奖励值为协同任务规划统一目标函数值。
基于统一目标函数(式(11)),建立本文所需求解问题的MDP模型。MDP的动作序列构成了统一目标函数中的决策变量,同时,其奖励函数中的奖励项由统一目标函数来表征。
2.2 改进的MCTS算法
对每一架无人机建立1棵蒙特卡洛树,对每棵树进行独立搜索,将搜索结果组成联合动作集,并代入联合奖励函数进行评价,最终将得到的奖励值返回至每一棵树,对每一棵树的结果节点进行回溯更新。
为了避免平均模拟结果对该问题求解结果产生影响,对式(12)中Q(v)/N(v)项进行改进,同时,保留式(12)中探索部分来避免局部最优解。改进的MCTS选择策略为
式中:Q(v)为基于所有无人机分配和突防决策得到结果。当某一无人机的突防动作矩阵不满足约束时,联合奖励函数会给所有的无人机策略赋予-0.2的惩罚值,这会导致其他结果较好的无人机策略得到一个较小的收益值,最终造成算法收敛变慢或者无法收敛的情况。为了解决此问题,让每棵搜索树同时记录该搜索树的单无人机统一目标函数值Ji,并将其作为选择策略的一部分来指导搜索。针对无人机i的搜索树,其选择策略可进一步改进为
式中:ξs和ξm分别为单无人机目标函数值权重因子和多无人机目标函数权重因子,其和为1。同时,对回溯更新公式(13)进行改进,在所提出的算法中,不再对节点信息中回报值进行累加,而是记录迭代学习过程中的最大值,并且记录每架无人机的单目标函数Ji的最大值。因此,改进的回溯更新公式可建立为
式中:ΔJi为第i架无人机在一轮模拟中得到的单无人机目标函数回报值。改进的MCTS 算法搜索框架如图1所示。
改进的MCTS算法伪代码如算法1所示。

算法1 改进的MCTS算法输入:建立NU棵蒙特卡洛树,输入其根节点1:while 当前学习步数小于预设总学习步数 do 2:for i in 1 to 无人机总数NU do 3:获得初始状态Sdis 4:while 当前节点状态v 非终止并且其动作已遍历选择过 do 5:通过式(19)选择下一节点v′6:v=v′7:end while 8:if v非终止 then 9:随机选择动作,扩展新节点v′10:使用随机模拟到达终止状态,获得单无人机的动作序列和ΔJi 11:end if 12:end for 13:构建目标分配矩阵X和突防动作矩阵M1,…,MNU,获得ΔQ 14:for i in 1 to 无人机总数NU do 15:通过回溯更新公式(20)从叶子节点向父节点更新16:end for 17:end while 18:最优目标分配矩阵X和突防动作矩阵M1,…,MNU
3 仿真验证
本文以50 架无人机(U1~U50)攻击5 个目标(T1~T5)为例,验证所提出的统一目标函数和改进MCTS算法的有效性。考虑目标威胁度和部署态势信息不同,给出目标威胁度和态势信息,如表4所示,其中,νTar代表目标的战略价值,Ndr、Ndsm、Ndmm、Ndlm分别代表目标依次部署的防御系统的数量。同时,每架无人机其初始航向角和对每个目标的协同攻击时间不同,不失一般性,随机产生各个无人机的航向和时间误差。部分无人机对目标的航向误差和时间误差如表5 所示。取λγ=1/3,λt=1/3,λv=1/3,由此可建立优势度矩阵A,在突防决策阶段,设置每种动作选择不超过b1=2 次以及机动动作选择不超过b2=6 次,式(10)中权重因子ρ1、ρ2、…、ρ50均取1/50。算法中Cp=,ξs=0.4,ξm=0.6,算法运行环境为i5-9400F 处理器,2.90 GHz,仿真环境为python3.6,总迭代步数设置为30 000步。

表4 目标价值和部署态势数量Table 4 Target value and deployment situation

表5 无人机对目标的航向和时间误差Table 5 Heading angle and time error of UAV to target
针对上述仿真问题的搜索空间为NUNTar×(NdNA)NU,则该工况的搜索空间为505×(75)50。显然,传统穷举法很难实现问题的优化求解。为此,本文使用原UCT 算法作为对比,以验证所提出算法的有效性。
3.1 实验1:改进的MCTS算法
经过30 000 步学习训练,训练总耗时为222.834 4 s。改进的MCTS 算法训练结果如表6 所示。为了方便动作序列的表示,用数字1至5分别表示隐身、转弯机动、跃升机动、俯冲机动和蛇形机动,用一维向量表示无人机依次经过部署区域所做出的动作序列。根据联合动作,综合目标分配和突防决策结果,得到最优统一目标函数值为J*=0.889 5。

表6 改进MCTS算法训练结果Table 6 Training results of improved MCTS algorithm
训练过程中每架无人机根据自身启发式因子进行独立搜索。以无人机U10、U20、U30、U40和U50 为例,得出训练过程中搜索深度和单无人机统一目标函数值Ji。图2所示为部分无人机在训练过程中的树搜索深度,在该问题中搜索深度表示无人机经过防空系统的数量。从图2 可以看出:在训练10 000 步后,树搜索能达到最大深度,说明无人机策略能在前期训练中根据奖励函数并基于随机模拟得到一个最优解的范围,在后面的训练中,主要在该范围中搜寻最优解。
部分无人机在训练过程中的目标函数值Ji如图3 所示。从图3 可见:在前期的训练中搜索深度较小,此时,搜索树靠随机模拟来获得回报值,但随着搜索深度增大,树将获得的较优解存储在节点信息中,并依靠启发式策略不断去搜寻最优解。在训练后期搜索过程出现了震荡现象,这是因为访问次数较少的节点的收益值大于了当前较优解的收益值,策略选择了访问次数较少的节点,以此来避免陷入局部最优。
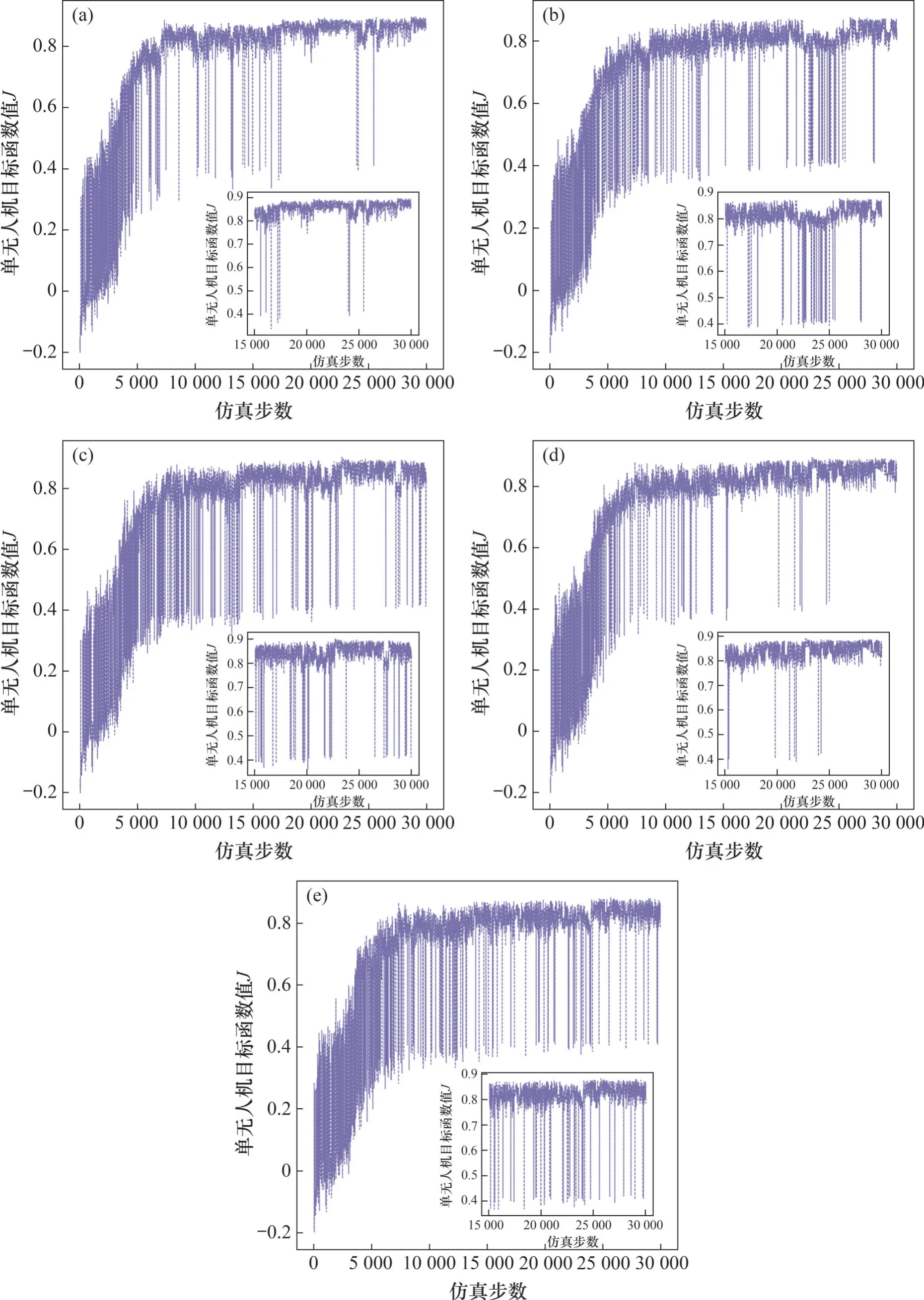
图3 部分无人机搜索树的目标函数值JiFig. 3 Objective function value Ji of partial UAV search trees
3.2 实验2:UCT算法
与所提出算法进行对照实验,同样设置总迭代步数为30 000 步,训练耗时为261.7256 s,UCT算法训练结果如表7 所示,得到统一目标函数值J*=0.857 2。对照实验部分结果如表8所示。
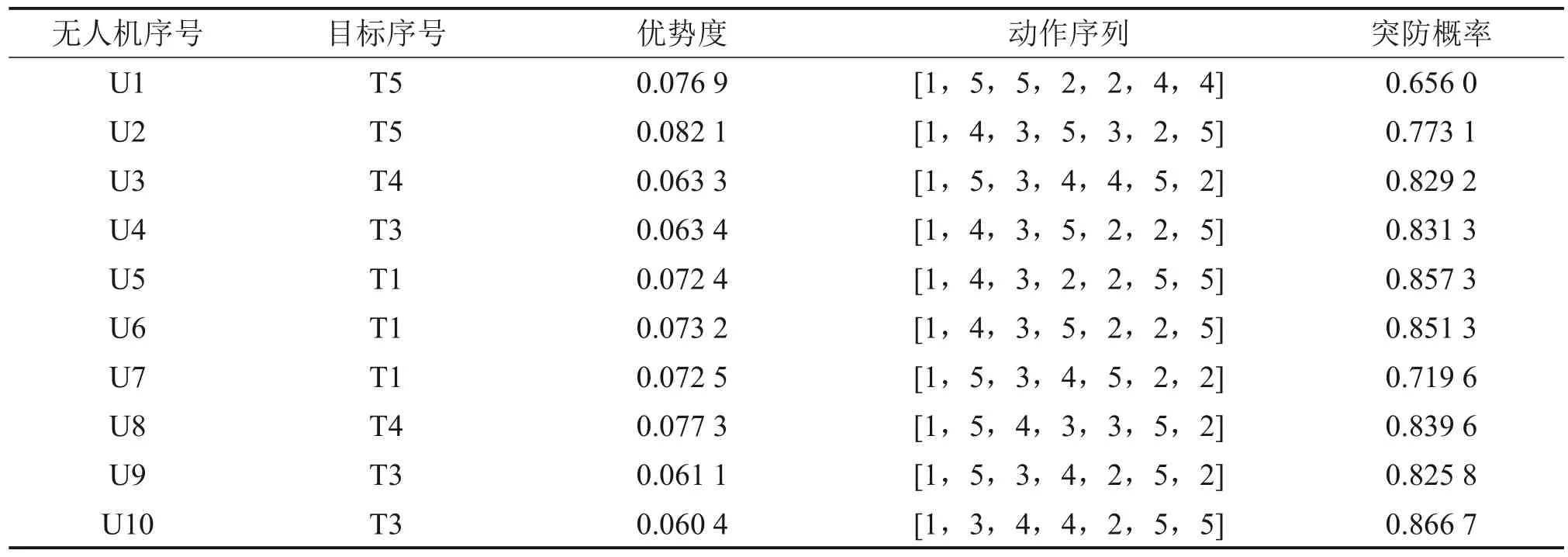
表7 UCT算法训练结果Table 7 Training results of UCT algorithm

表8 训练结果对比Table 8 Comparison of training results
从表8 可见:与UCT 算法相比,本文所提出的方法在收敛程度以及训练时间上更有优越性。其中,鉴于改进的MCTS 算法对选择策略和回溯更新公式进行了改进,其更符合组合优化问题的求解特点;同时,在相同迭代步骤下,相比于UCT,所提出算法的训练时间减少了15%左右。这是因为传统UCT 算法在迭代过程中需要更多的累加和除法计算,改进算法舍弃了这些步骤,因此,所设计的统一目标函数能有效指导改进算法进行学习。
4 结论
1) 探讨了多无人机目标分配问题和突防决策问题之间的耦合关系。基于无人机协同突防中的优势度模型和突防概率,构建了一种多无人机作战任务规划统一目标函数。同时,分阶段建立了该问题的强化学习框架,并提出了一种改进的MCTS算法,对目标分配和突防决策2个问题进行了统一求解。
2) 在对比仿真实验中,所设计的统一目标函数能有效指导改进的MCTS 算法进行学习。该算法的收敛效果好,相比于传统的蒙特卡洛搜索算法,训练时间减少了近15%。
