高中物理习题详解文案的编制

摘   要：结合教学实际，以2022年高考湖南卷第14题为例，详细介绍了以学情诊断为基础，以思维显化为关键，以推理建模为核心，以拓展变式为辅助的习题详解文案编制。通过详解文案中審题、建模、表示、计算等关键要素的处理，解决学生懂而不会、会而不对、对而不全、全而不美的问题。同时也为教师在有限课堂教学时间中处理情境多变、过程复杂、计算繁琐的习题提供教学参考。

关键词：学情诊断；思维显化；推理建模；拓展变式

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2023）9-0042-6

收稿日期：2023-03-29

基金项目：重庆市渝中区教育科学“十三五”规划2019年度课题“核心素养导向下普通高中物理教科书‘做一做’栏目的运用研究”（2019-14）；重庆市渝中区教育科学“十四五”规划2021年度课题“基于‘双新’背景下的高中物理新教材情境化习题的应用研究”（2021-YB-03）。

作者简介：李峥（1985-），男，中学高级教师，主要从事高中物理教学工作。

1    问题的提出

习题教学是物理教学的关键环节，是形成物理观念、培养科学思维最为有效的方式和手段。然而，课堂教学中却普遍存在高速而压缩化的课堂教学进度与缓慢而复杂的学生学习历程的落差，习题教学中的问题主要体现在以下方面：

（1）从教学目标的角度看，教师以习题解答的过程为要点，而忽略了习题对概念建构、知识关联、能力培养的显性作用。教师缺乏对学生学习需求的分析，弱化了习题对培养学生理解能力、推理论证、模型建构、科学探究及创新思维等方面的功能。

（2）从教学内容的角度看，教师较为注重对习题的过程分析，而对学生如何将物理情境转化为物理问题，再将物理问题转化为数学问题的思维显化过程不够重视，对习题的总结、归纳、提炼不够，很难实现举一反三、触类旁通的目的。

（3）从教学进度的角度看，教师较为注重习题讲解的完成度，而学生的思维进度往往较为滞后，很容易出现教师讲授与学生学习进度不相匹配，导致学习任务的跳跃式过程，容易形成学生思维上的堵点和阻点。

（4）从教学设计的角度看，教师往往以自我教学经验为中心，较少从促进学生的学习角度上进行学习设计，使得学生学习过程中形成大量的“不懂或不理解”的“夹生”，导致学生陷入无法解决、不能突破、无法澄清的学习困境。

（5）从教学效果的角度看，习题教学主要以教师的讲授为主，学生很难对解答过程进行复盘，更谈不上课后进行自我的巩固和复习，特别是当参考答案和教师讲授不一致时，更容易导致学生陷入“迷思”。长此以往，学生会缺乏解决问题的能力和信心。

2    习题详解文案的编制

习题详解文案是在充分了解学生学情的基础上，结合教学实际，编制学生能够“看得懂”“跟得上”“用得来”的习题教学案。其显著特征是将习题解答的“隐性”思维过程通过文字说明、公式表达等“显性”呈现出来，帮助学生明确如何进行信息提取、模型建构、逻辑推理和数学表达。通过审题、建模、表示、计算等关键要素的处理，帮助学生厘清习题的难点及易错点，形成相应的解答规范和通解通法。利用变式训练和拓展练习，帮助学生完成思维进阶，形成对此类型题目的深度认知和理解。

2.1    基于学情诊断，强化需求把握

学情诊断是习题详解文案编制的基础。常用的方式为调查访谈、课堂反馈及作业批改。从教学实际看，造成学生习题解答懂而不会、会而不对、对而不全、全而不美的原因主要有以下两方面：

（1）学科知识方面：知识遗忘，知识碎片化或概念规律理解不深；

（2）素养能力方面：不能有效进行题目信息提取，不能基于真实的情境建构物理模型，学科逻辑思维不够严密，计算能力、表达能力欠缺。

而要真实把握学习需求，还需要基于精准数据的学情分析，从2022年湖南卷第14题年级测试结果来看，0～5分占比为70.5%，5～10分占比为24.55%，10～15分占比为4.95%。结合审题、建模、表示、计算等解题要素，设计调查问卷如表1所示。

对应的数据统计表如图1所示。

通过数据分析，审题要素中存在问题占比最高的为过程分析，有56.5%的学生不能有效建立过程联系；在建模要素中，有52.7%的学生无法将真实情境抽象成物理问题，有61.1%的学生无法关联对应的物理模型；在表示要素中，有48.9%的学生不能将文字条件转化为数学条件，有51.9%的学生在运用运动学公式或功能关系公式中出现错误或疏漏；在计算要素中，有49.6%的学生不能有效进行等比数列的递推运算，而有62.6%的学生在解答过程中不能有效地进行多字母未知量的代换，导致浪费了大量的计算时间。

而学生普遍对“N次拍击，每次给大小相等的冲量I”和“拍击一次，给NI大小的冲量”是否等效存在困惑，虽然能够感性地认识到碰撞过程中存在能量的损耗，但是没有上升到理性的认知，存在理解的阻点。

2.2    注重思维显化，细化推理建模

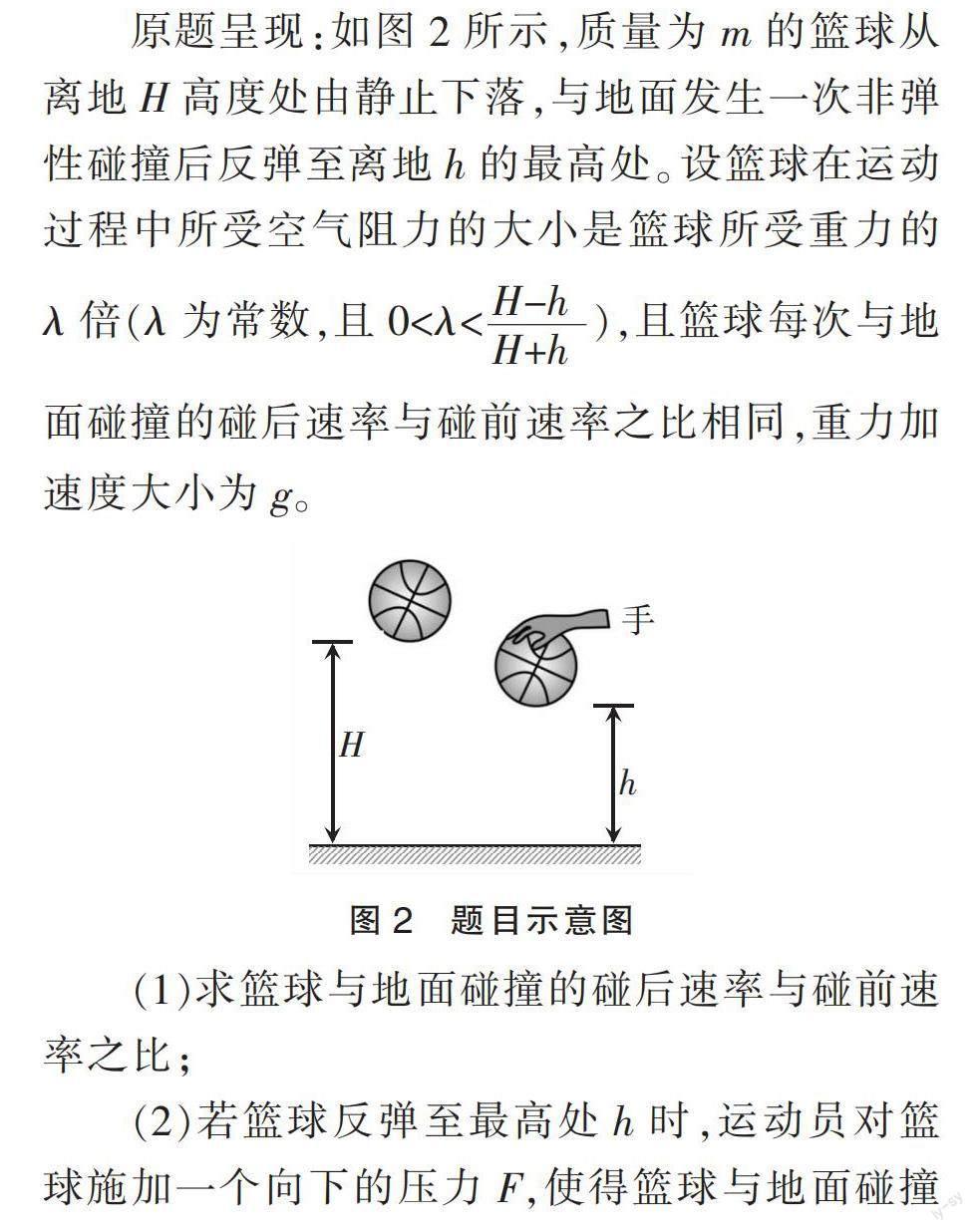
原题呈现：如图2所示，质量为m的篮球从离地H高度处由静止下落，与地面发生一次非弹性碰撞后反弹至离地h的最高处。设篮球在运动过程中所受空气阻力的大小是篮球所受重力的λ倍（λ为常数，且0<λ<），且篮球每次与地面碰撞的碰后速率与碰前速率之比相同，重力加速度大小为g。

（1）求篮球与地面碰撞的碰后速率与碰前速率之比；

（2）若篮球反弹至最高处h时，运动员对篮球施加一个向下的压力F，使得篮球与地面碰撞一次后恰好反弹至h的高度处，力F随高度y的变化如图3所示，其中h0已知，求F0的大小；

（3）篮球从H高度处由静止下落后，每次反弹至最高点时，运动员拍击一次篮球（拍击时间极短），瞬间给其一个竖直向下、大小相等的冲量I，经过N次拍击后篮球恰好反弹至H高度处，求冲量I的大小。

问题1：题目的已知条件是什么？需要求解的問题是什么？

已知篮球质量为m，静止释放高度为H，反弹高度为h，空气阻力为λmg，需要求解碰后和碰前的速率之比，力F0的大小，冲量I0的大小。

问题2：篮球与地面碰前、碰后的速率如何计算？

设篮球与地面碰前的速率为v，碰后速率为v，下降过程中的加速度大小为a，上升过程中的加速度大小为a，根据牛顿第二定律可得mg-λmg=ma，a=（1-λ）g；mg+λmg=ma，a=（1+λ）g；v=2（1-λ）gH，v=2（1+λ）gh；碰后与碰前的速率之比k==。

问题3：从力F随高度y的变化关系可求出什么物理量，如何表示？

从力F随高度y的变化关系可求出力F所做的功W，根据图像面积可得W=（h-h0）F0。

问题4：如何求F0的大小，选用什么公式或定理？

可以利用动能定理，设外力作用后篮球与地面碰前的速率为v'，则碰后的速率v'=kv'，从外力作用到篮球落地，mgh+W-λmgh=mv；从篮球落地到反弹到最高点，-mgh-λmgh=0-mv，联立可得F0=。

问题5：拍击时间极短如何理解？给篮球的冲量I相当于提供了什么？

由于拍击时间极短，重力的冲量可忽略不计，则根据动量定理有I=mv，即每拍击一次篮球将给它一个速度v。

问题6：第一次拍击后篮球下降的高度h和反弹上升的高度h如何表示，它们之间存在怎样的关系？

设第一次拍击后篮球与地面碰前速度为v1，碰后速度为kv1，则v-v2=2（1-λ）gh，（kv1）2=

2（1+λ）gh，代入k=可得

问题7：能否推理得到第二次、第三次……第N次拍击后篮球反弹上升高度和最初下降高度之间的关系？

设第二次拍击后篮球与地面碰前速度为v2，碰后速度为kv2，第三次拍击后碰前速度为v3，碰后速度为kv3……第N次拍击后碰前速度为vN，碰后速度为kvN，篮球运动的情境如图4所示。

问题9：“N次拍击，每次给大小相等的冲量I”和“拍击一次，给NI大小的冲量”是否等效？

若拍击一次，根据动量定理NI=mNv，相当于给篮球Nv的初速度，拍击后篮球与地面碰前速度为v'1，碰后速度为kv'1，则

分析可知，阻力不是影响两种形式是否等效的因素。

设计意图：利用问题驱动显化思维过程，帮助学生明确推理逻辑。利用情境图像，建立等量关系，帮助学生建构运动模型。针对学情诊断，聚焦难点、阻点，帮助学生厘清迷思概念。

2.3    利用拓展变式，优化思维进阶

拓展（1）：若H=h，在不施加外力的情况下，求经过多少次碰撞篮球上升的最大高度小于H？

因为=，所以篮球每次与地面碰撞前后的高度之比是个定值，所以hn=H（）n，经三次碰撞后篮球上升的高度为h3=H（）3=H<。

变式（1）：（2020年全国Ⅱ卷25题）如图5所示，一竖直圆管质量为M，下端距水平地面的高度为H，顶端塞有一质量为m的小球。圆管由静止自由下落，与地面发生多次弹性碰撞，且每次碰撞时间均极短；在运动过程中，管始终保持竖直。已知M=4m，球和管之间的滑动摩擦力大小为4mg，g为重力加速度的大小，不计空气阻力。（第1问略）（2）管第一次落地弹起后，在上升过程中球没有从管中滑出，求管上升的最大高度；（3）若管第二次落地弹起的上升过程中，球仍没有从管中滑出，求圆管长度应满足的条件［1］。

解析 设第一次弹起过程中球相对管的位移为x1，在管开始下落到上升H1这一过程中，由动能定理有Mg（H-H1）+mg（H-H1+x1）-4mgx1=0。结合第二问中的计算结果（计算过程略）H1=H，代入题给数据得x1=H。

同理可推得，管与球从再次下落到第二次弹起至最高点的过程中，球与管的相对位移x2为x2=H1。

设圆管长度为L。管第二次落地弹起后的上升过程中，球不会滑出管外的条件是x1+ x2≤L，L应满足的条件为L≥H。

拓展（2）：冲量I的求解是否还有其他的方法？

变式（2）：（2015年天津卷12题）现代科学仪器常利用电场、磁场控制带电粒子的运动。在真空中存在着如图6所示的多层紧密相邻的匀强电场和匀强磁场，电场和磁场的宽度均为d。电场强度为E，方向水平向右；磁感应强度为B，方向垂直纸面向里。电场、磁场的边界互相平行且与电场方向垂直，一个质量为m、电荷量为q的带正电粒子在第1层电场左侧边界某处由静止释放，粒子始终在电场、磁场中运动，不计粒子重力及运动时的电磁辐射。

若粒子从第n层磁场右侧边界穿出时，速度的方向与水平方向的夹角为θn，试求sinθn。

解析 设粒子在第n层磁场中运动的速度为vn，轨迹半径为rn（各量的下标均代表粒子所在层数，下同）。则有

粒子进入第n层磁场时，速度的方向与水平方向的夹角为αn，从第n层磁场右侧边界穿出时速度方向与水平方向的夹角为θn，粒子在电场中运动时，垂直于电场线方向的速度分量不变，有

由图7可以看出

联立（2）（3）（4）式可得

由（5）式看出r1sinθ1，r2sinθ2，…，rnsinθn为一等差数列，公差为d，可得

当n=1时，由图8看出r1sinθ1=d（7）

本题也可以利用正则动量进行求解，粒子从第n层磁场右侧边界穿出时，x方向在磁场中的位移为nd，与y方向上速度变化量Δvy的关系为qBnd=m·Δvy，若出磁场时速度方向与水平方向夹角为θn，则［2］

设计意图：利用问题拓展，挖掘习题资源，培养学生创新思维。利用变式练习，强化类型训练，培养学生思辨能力。

3    小  结

习题详解文案的编制首先需要“精细化”，即将解题的思路通过问题引导，结合详细的情境图示或文字说明，让学生能够“听得懂”“跟得上”，即便课堂“掉线”也能在对应的环节进行标记，方便课下及时复盘和弥补；其次需要“个性化”，即要做到一题一案或一类一案，要能针对性地解决学生个性化或共性化问题，同时要注重类型问题的总结、归纳、提炼、延伸和拓展；最后需要“重复性”，即要形成电子文档，能够根据教学要求不断进行调整和补充，形成可持续、可发展的教学资源。

习题详解文案的编制要通过数据分析强化学情诊断，通过有效设问显化思维逻辑，通过细化解析突破重点、难点，通过变式拓展实现思维进阶。而编制过程中则要结合审题、建模、表示、计算等要素进行精细化设计，从而帮助学生走出课堂困境，实现物理学科能力的提升。

参考文献：

［1］李勇.2020年高考物理全国Ⅱ卷第25题的多种解法探析［J］.物理教学，2020，42（12）：61-63.

［2］崔琰，马朝华.2015年天津高考物理压轴题第2问的巧解［J］.物理教学探讨，2015，33（12）：41-42.

（栏目编辑    陈  洁）