横缝对高拱坝系统非线性地震响应的影响分析

杜成斌 李 云 杜宁宇 江守燕

(1.河海大学 力学与材料学院, 南京 211100;2.河海大学 河海里尔学院, 南京 210098)

拱坝作为一种特殊的混凝土结构,其抗震性能受到很多因素的影响,包括拱坝的形状、大小、材料、基础等.因为拱向作用的影响,坝体上的荷载从大坝的中心分向两侧的坝肩.为了减少混凝土浇筑产生的大量水化热的影响,拱坝结构一般设计若干条横缝,同时为了增加坝体的整体性,横缝内又设置一些键槽.徐强等[1]以相对位移、横缝开度和损伤体积比作为评价指标,评估了在强地震动作用下坝体混凝土材料的随机性对拱坝抗震性能的影响;秦礼君等[2]以白鹤滩拱坝为例,考虑30条坝体横缝建立了拱坝-地基三维有限元模型,以基于坝段的抗滑安全系数及抗滑安全系数持时作为局部安全评价指标,研究了两个指标随地震动峰值加速度的变化规律及其沿坝段高程的分布规律;马天骁等[3]考虑了坝体混凝土及坝基岩体的损伤等材料非线性问题以及横缝开合等接触非线性问题,研究了特高拱坝—坝基的动力损伤行为;陈灯红等[4]研究了库水压缩性及分缝布置对拱坝非线性地震响应的影响,探讨了设有13条横缝和不设横缝对坝体动力响应的影响;李晓娜等[5]通过采用局部连续-非连续变形动态接触算法,考虑横缝、裂缝接触非线性,无限地基的辐射阻尼效应,以及坝体-库水的相互作用,对某高拱坝抗震性能进行了分析.由于横缝条数越多,数值模拟的难度也就越大,以前曾有学者得出3条或5条横缝可大致得出横缝的最大开度,但显然这个结果与横缝位置布置、径向摩擦情况等都有关系,需要进一步研究,以便对横缝对大坝整体的地震响应有正确的认识和把握.

横缝的抗拉强度非常小,甚至没有抗拉强度,地震作用下横缝会反复地张开-闭合,为了保证大坝分析结果的可靠性,有必要同时考虑几何和材料的非线性来研究大坝结构性能.论文为探究拱坝遭遇强震时的非线性地震响应规律,建立拱坝-地基-库水相互作用的有限元模型,采用混凝土损伤塑性本构模型模拟材料的非线性特性,指数型动接触本构模型模拟各个坝段之间的横缝接触作用,分析探讨横缝数量、径向不同摩擦因数对拱坝非线性地震响应的影响.

1 混凝土损伤塑性本构模型

混凝土损伤塑性本构模型[6]适用于模拟循环荷载作用下混凝土的特性.该模型认为混凝土材料有两种主要的破坏机制:拉伸开裂和压缩破坏.

在塑性增量理论中,总应变张量ε被分解为弹性部分εe和塑性部分εp,即

假设变量为{εe,εp,κ}的非线性局部问题的状态在时间t已知.应力张量由下式给出

式中:E0是材料初始(未损坏)弹性刚度;d是刚度退化变量(标量),取值范围为0(未损伤)到1(完全损伤).与混凝土破坏机制(开裂与压碎)相关的损伤导致弹性刚度的降低,弹性刚度被认为是由拉伸和压缩损伤变量组成的一组内部变量κ的函数,即κ={κt,κc}.

用单轴拉伸下的应力-开裂应变曲线和单轴压缩下的应力-压损应变来定义弹性、塑性和损伤行为.现行规范[7]规定了混凝土单轴受压与受拉下的应力-应变曲线以及损伤参数的计算公式.混凝土单轴受拉的应力-应变曲线方程可按下列公式确定

式中:αt(αc)为混凝土单轴受拉(受压)应力-应变曲线下降段的参数值,按现行规范[7]中表C.2.2(C.2.3)取用;f*t(f*c)为混凝土的单轴抗拉(抗压)强度;εt(εc)为与单轴抗拉(抗压)强度f*t(f*c)相应的混凝土峰值拉(压)应变,按现行规范[7]中表C.2.2(C.2.3)取用;dt(dc)为混凝土单轴受拉(受压)损伤演化参数.

2 横缝缝面接触本构模型

2.1 法向接触行为

采用指数型接触本构模型模拟缝面之间的法向接触行为,接触压力p-嵌入量h之间的本构关系如图1所示,可表达为

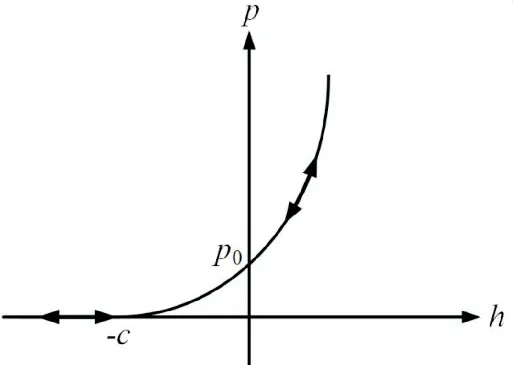
图1 法向接触压力-嵌入量(p-h)关系

式中:p0为嵌入量h=0时的接触正应力,取p0=50 GPa;c为接触间隙,是判断接触状态的指标,取c=5 μm.

2.2 切向接触行为

采用库伦摩擦模型模拟切向接触行为,实际工程中为提高设置横缝后坝体的整体性,分段浇筑时会在各个横缝之间设置键槽.常见的键槽形式有梯形键槽、球形键槽等,但实际键槽建模时会存在一定的困难.论文将键槽作用进行简化,采用缝间设置弹簧单元来近似模拟键槽的切向限制作用,这些弹簧单元连接相邻坝段之间接触面上的节点,在切向设置较大的弹簧刚度限制坝段之间切向的相对滑动,如图2 所示.

图2 切向约束弹簧示意图

2.3 接触模型验证

如图3(a)所示,一刚性梁竖直放置在刚性地基上并与其接触.根据输入地面加速度¨ug(t)、宽高比B/H和摩擦因数μ的不同,其运动模式可能包括滑动、翻转及其混合模式.图3(b)中θ为模型底面与地基的夹角,当θ＞0时,物体顺时针旋转.

图3 刚性梁及其运动示意图

梁的密度取100 kg/m3,接触主表面选择为地基,从表面为梁的底面,法向接触行为如2.1节所述.地基设置竖向约束,水平向为加速度边界.输入的地面加速度[8]如图4所示.

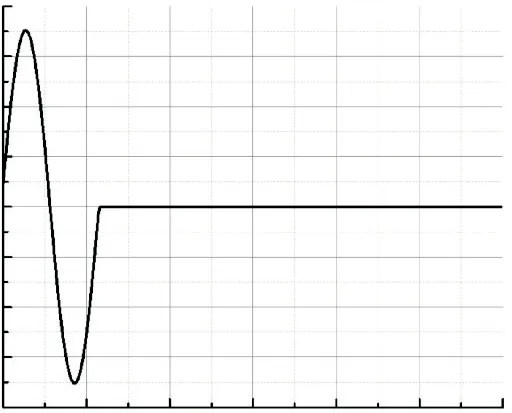
图4 输入的地面加速度时程

图5给出了模型底面与地基的夹角θ随时间变化的曲线,并与文献结果[8]进行了对比.从图中可以发现,模型首先向左旋转,夹角θ为负值,随着地面运动逐渐顺时针旋转.采用前述动接触模型模拟的结果与文献[8]较为接近,可以验证动接触模型在模拟面与面接触时的准确性.

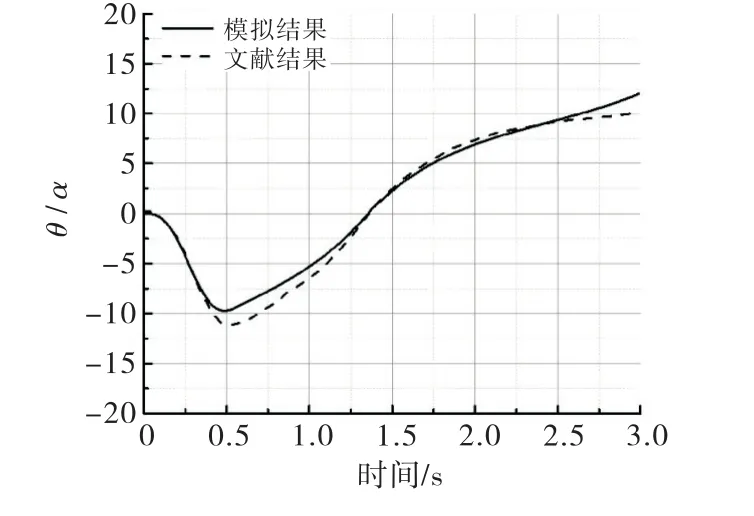
图5 模型旋转响应时程曲线

3 某高拱坝系统的地震响应分析

3.1 有限元模型

以某混凝土高拱坝为例,该混凝土拱坝为抛物线形变厚度双曲拱坝,共设置了40 条横缝,最大坝高292 m.拱坝-地基-库水整体模型有限元网格如图6所示,地基范围延伸约2倍最大坝高,整体模型单元数为28966,结点数为35968,其中坝体单元数为5248,结点数为7 865.

图6 拱坝-地基-库水系统有限元模型

坝体、地基材料参数取值[9]见表1,参照现行规范[10],动力分析时坝体混凝土弹性模量取为静弹模的1.5倍.混凝土损伤塑性模型部分参数见表2.

表1 材料参数

表2 混凝土损伤塑性模型部分参数

图7为计算中采用的混凝土单轴拉伸(压缩)本构/损伤曲线.坝体采用瑞利阻尼假设,阻尼比取为5%;坝基采用无质量地基模型;大坝-库水动力相互作用采用规范规定的附加质量法进行简化.为了得到较为显著的横缝非线性特性,模拟运行低水位工况,水深228 m.地震输入加速度时程曲线如图8所示,顺河向、横河向峰值加速度约为0.308g,竖直向取为水平方向的2/3.

图7 混凝土单轴拉伸(压缩)本构/损伤曲线

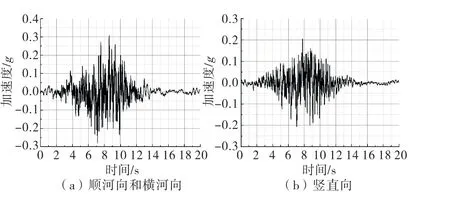
图8 输入地震加速度时程曲线

为探讨横缝数量对坝体地震响应的影响,设置了7种工况(见表3),模拟的横缝数量最多为40条.

表3 横缝分布工况

3.2 横缝数量对大坝地震响应的影响

1)横缝开度

图9～10给出了不同横缝数量与不同间距的各个工况下上下游横缝顶部开度极值曲线,横缝数量从1条到40条,间距从80～20 m,共设置了7种不同工况.从图中可以看出,上游面与下游面的整体规律是一致的,同一条横缝的上游与下游面的差值较小,基本都在1 mm 以内.

图9 1-11条横缝工况下的横缝开度极值

从图9可以看出,1和3条横缝的工况并未产生明显的开合.再往外增加两条时,也就是5条横缝的时候,靠近左岸的一条横缝有些许张开的迹象,但是开度值较小,只有5 mm 不到,这表明该工况下坝体左岸受到的响应可能大于右岸.7条横缝工况下靠近两岸的两条横缝张开程度较大,且相较于11条横缝工况中相同的两条横缝,其极值还要大一些.

进一步的验证可以从图10得到,图10给出了3种均布横缝的工况,包括11、21以及40条横缝3种,横缝间距分别是80、40以及20 m.首先观察整体可以发现3种工况大体上的极值分布规律相同,中间横缝开度较小,靠近两岸的横缝开度较大.对比3条曲线可以看出,11条横缝工况的开度极值总体上大于21和40条横缝的工况,即随着间距以及数量的增加同一位置处的横缝开度极值会有一定的下降.而且可看出,7条横缝的最大开度基本同11、21和40条横缝的最大开度相近,且位置大致相同,均为靠近左右坝肩的横缝.

图10 11-41条横缝工况下的下游横缝开度极值

2)坝体损伤分布

图11给出了7种工况下坝体最终损伤云图,损伤主要分布在坝体底部,且两边损伤程度大于中间部位.从底部损伤云图分布可以看出,左岸的损伤程度大于右岸.1、3 和5 条横缝工况的损伤情况较为接近,因为这几种工况横缝均设置在坝体中部区域,由前文可知该模型中部的横缝非线性效应较弱,所以3种工况损伤情况接近也较为合理.

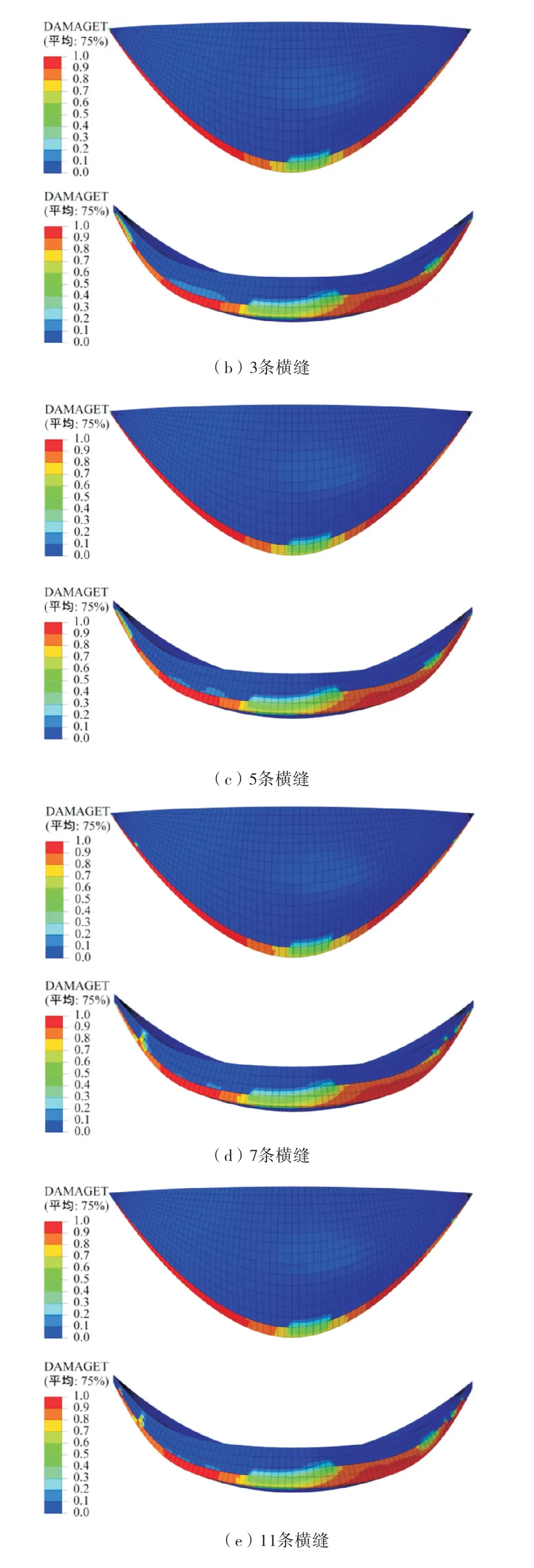
图11 不同横缝分布工况下坝体损伤云图

当横缝增加到接近岸边的区域时,损伤分布情况有一定的变化.首先从7条横缝工况开始,观察上游面损伤云图可以发现,随着横缝数量的增加以及间距的减小,坝体接近岸边部位的损伤有所下降.但是由于两边设置了横缝,在地震作用下横缝张开时虽然释放了拱向的拉应力,但是增大了梁向的作用,从底部损伤图可以看出,底部损伤面积有所变大,但是损伤的程度有所减小.横缝数量与间距对坝体遭遇地震时的非线性响应有明显的影响,在仿真模拟中不可忽视,增加横缝数量且缩小相邻横缝的间距可以显著降低坝体的损伤程度.

3.3 径向取不同摩擦因数时横缝开度和大坝响应

为研究径向取不同摩擦因数时横缝开度和大坝的地震响应情况,将加速度峰值放大1.5倍,这里不计坝体材料非线性.以7条横缝工况为例,计算考虑的荷载组合同前(低水位+地震).图12给出了摩擦因数分别取0.0,0.2,0.4,0.6,0.8时的第1条横缝(J1)和第4条横缝(J4)的张开闭合过程.表4为取不同摩擦因数时,各种情况的横缝开度极值和顺河向的位移极值.

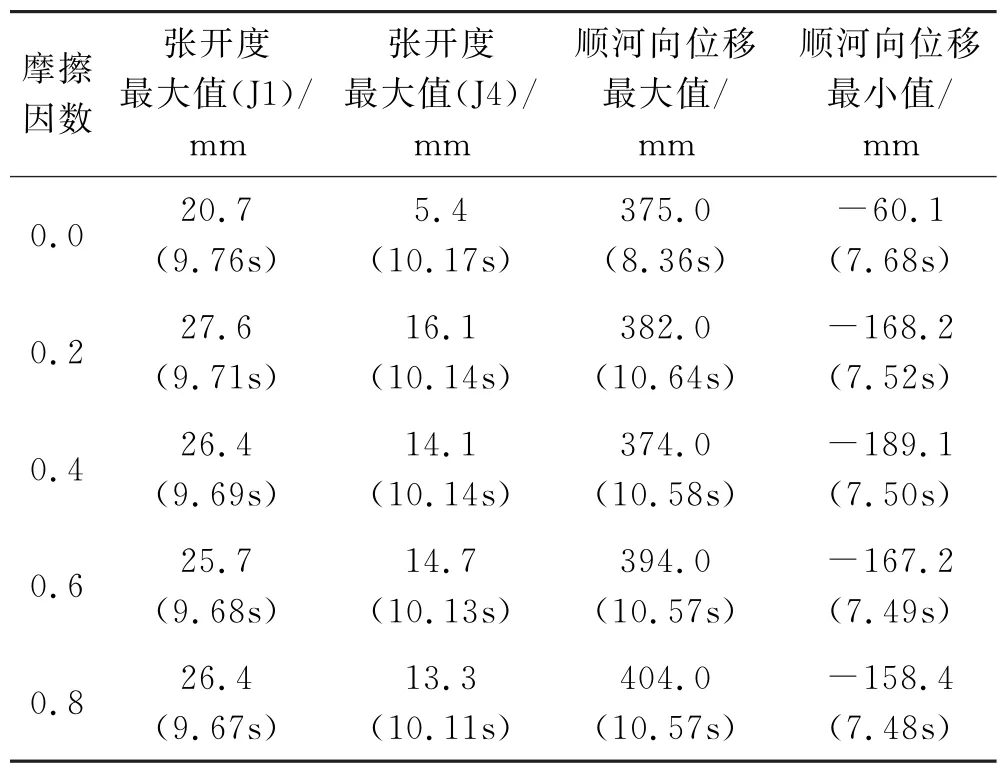
表4 不同摩擦因数时横缝开度极值和顺河向位移极值(单位:mm)

图12 横缝坝顶张开闭合曲线

由图12知,不同摩擦因数时,J1和J4缝的张开闭合规律都非常一致,出现极值的时刻也比较接近,结合表3知,径向自由时横缝开度极值要小于缝面有径向摩擦的情况,摩擦因数取0.2 时张开度最大,比径向自由时的J1 和J4 缝张开值分别大33.3%、198.1%左右;这符合大坝系统振动能量分布规律,即假定大坝系统振动能量为一定值时,径向自由时大坝径向振动的能量要大于横缝径向有摩擦情况,就有可能导致后者的横缝张开闭合运动大于前者;随着摩擦因数的逐渐增大,总的趋势是横缝开度极值略有减小.不考虑横缝径向摩擦因数,由后面的时程曲线知,有较大的向下游位移,在这样的初始条件下,大坝的向上游和向下游的动位移相对小于径向有摩擦情况.尽管有摩擦因数时坝体顺河向位移的极值有所差别,但每种情况的极值的变化范围基本一致,在550.2～563.1 mm 左右,其中摩擦因数0.2时极值的变化范围最小.

图13给出了不同摩擦因数时拱冠处的顺河向和横河向位移响应.

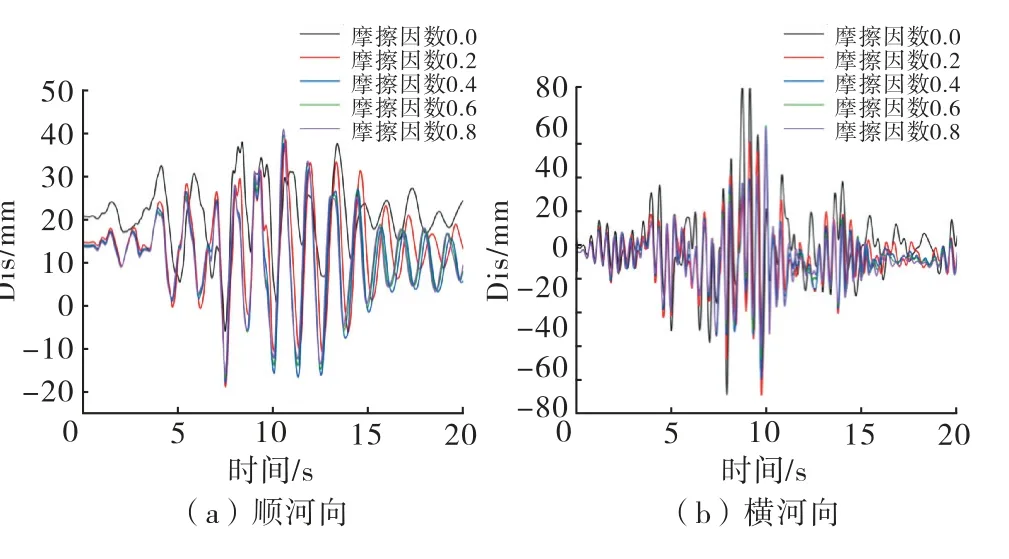
图13 上游面坝顶拱冠处位移时程曲线

选取坝体上游面靠近坝顶拱冠位置的拱向应力,靠近中间横缝的坝踵位置的梁向应力,列如表5 所示.

表5 坝体上游面的最大拱向、梁向应力(单位:MPa)

由图13知,缝面径向自由时,在静荷载下,顺河向的初始位移就明显大于缝面径向有摩擦的情况,摩擦因数越大,初始位移越小;缝面自由时横河向位移响应明显要大于径向有摩擦时的情况.当摩擦因数增大到一定数值后,顺河向、横河向位移响应逐渐趋于一致.

坝体上游面顺河向位移向下游面最大时,梁向拉应力较多出现在坝踵靠近中间横缝的位置,拱向压应力较多出现在坝体中间偏上的位置、或坝顶左右;坝体上游面顺河向位移向上游最大时,梁向压应力较多出现在坝踵中间偏左的位置,拱向拉应力较多出现在坝体坝肩的位置.由表4可知,考虑横缝的张开,上游面的最大拱向拉应力均很小,考虑径向有摩擦因数时,拱向压应力有所增加,梁向拉应力有所增加.

4 结 论

本文对某高拱坝-地基系统进行了地震作用下的非线性地震响应模拟,重点探究了高拱坝在遭遇强震时横缝的非线性效应.研究得到以下结论:

1)7条横缝模拟时的最大开度与11、21和40条横缝模拟的结果接近,对于实际有几十条横缝的高拱坝,可以用少量的、合理布置的横缝进行模拟,给出合理的横缝开度值.

2)最大开度的横缝不一定在拱冠位置,在靠近左右坝肩附近的横缝,由于坝肩端部约束的影响,也会使接近端部约束的横缝产生较大的开度.

3)缝面考虑径向摩擦因数的横缝开度要大于径向自由的横缝开度.

4)摩擦因数增加到一定时,顺河向位移响应曲线基本一致.

实际拱坝的横缝是带有球形键槽的,横缝的张开、闭合和滑移是一个复杂的非线性过程.影响高拱坝地震响应的因素还有非均匀地震动输入、坝水相互作用等,今后需继续研发先进的计算理论、建立精细化的力学模型,继续进一步深入探究复杂条件下带横缝高拱坝的地震响应,为高拱坝抗震安全评估提供可靠的依据.

(致谢:本文在拱坝建模与计算中得到了河海大学李斌硕士的帮助,特此表示感谢.)