防屈曲支撑外伸连接段破坏失效机理及试验研究

2023-10-12吴克川戴必辉余文正张龙飞

工程科学与技术 2023年5期

吴克川，陶忠，潘文，戴必辉，兰香，余文正，张龙飞

(1.昆明学院建筑工程学院，云南昆明 650214；2.昆明理工大学建筑工程学院，云南昆明 650500；3.西南林业大学土木工程学院，云南昆明 650224)

防屈曲支撑（BRB），是一种兼具耗能与承载双功能的消能减震构件[1]，主要由核心耗能单元与外围约束单元组成，其通过限制核心单元的受压失稳获得较高的稳定承载力[2]。具有足够的稳定性、良好的低周疲劳特性及合理的构造措施是防屈曲支撑发挥优越滞回性能的前提。目前，防屈曲支撑的稳定设计方法[3]及设计理论[4]较为成熟，整体稳定性[5]及局部稳定性[6]均较易保证，低周疲劳寿命也随着低屈服点钢材的应用而逐步提高。同样，研究者们针对防屈曲支撑的组成提出了各种不同的构造形式，以保证和提高其稳定工作性能[7]，但大多数研究集中在防屈曲支撑截面构造形式[8]、约束部件构造形式[9]及板件比例尺寸构造[10]的合理性上。尽管防屈曲支撑有较为成熟的设计方法，但其仍时常出现外伸连接段的失稳破坏[11]，主要包括过渡段的平面内失稳破坏[12]及平面外失稳破坏[13]、全钢BRB约束单元端部的平面内破坏[14]及过渡段根部的破坏[15]。

针对防屈曲支撑外伸连接段的失稳破坏，Zhao等[16]基于边缘纤维屈服准则建立了BRB外伸连接段的稳定设计准则；Takeuchi等[17]对比了外伸段长度、约束非屈服段长度、外伸段刚度等因素对其稳定性的影响，并提出了限制外伸段失稳破坏的设计方法；朱博莉等[18]分析了荷载偏心对防屈曲支撑外伸段失稳破坏的影响，并进行了有限元验证分析；Hikino等[19]通过振动台试验验证了BRB较小的外伸段刚度及较小的约束非屈服段长度将降低其外伸段的稳定性能。观察已有研究[11-15]中出现外伸段失稳破坏BRB连接端部的构造形式及破坏形态，发现各BRB的部分过渡段处于无约束状态，是BRB的轴向薄弱环节，并且各BRB大都采用具有较大连接长度的高强螺栓方式进行连接。

基于Das[20]、Kinoshita[21]、郭彦林[22]、Sitler[23]及Takeuchi[24]等试验过程中出现的BRB外伸段破坏形式及特征，分析BRB外伸连接段的破坏失效机理，提出改善外伸连接段稳定性能的端部构造形式，建立相应的外伸连接段稳定分析模型；设计并制作3根端部构造形式改进后的全钢防屈曲支撑，通过拟静力试验验证所提出端部构造形式的合理性以及稳定分析模型的有效性，以供BRB产品设计参考。

1 BRB外伸连接段破坏失效机理

1.1 失稳破坏过程

防屈曲支撑组成及其高阶多波屈曲如图1所示。由图1（a）可见，防屈曲支撑主要由核心耗能单元与外围约束单元组成。其中，核心耗能单元由外伸连接段、过渡段及耗能段串联而成。由图1（b）可见，当支撑两端作用的轴向力P超过其屈服承载力时，耗能段将出现高阶多波屈曲模态[25-26]，这可能是引起支撑端部转动的最直接原因。

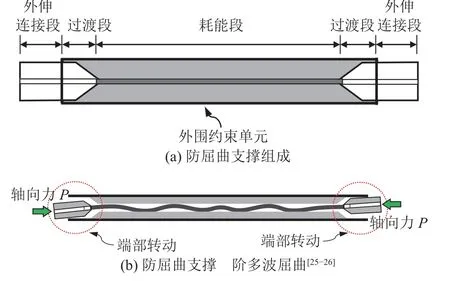
图1 防屈曲支撑组成及其高阶多波屈曲Fig.1 Composition of BRB and its high-order multi-wave buckling mode

由于耗能单元与约束单元间存在一个微小的间隙，当支撑端部的转动变形尚未超过该间隙值时，支撑端部可以自由转动；随着轴向力P的增大，支撑端部的转动变形也随之增加，直至支撑外伸连接段与约束单元边缘产生横向点接触，并产生横向接触力，出现BRB外伸连接段失效模式1，如图2所示，此时该转动变形受到约束单元的限制。由图2可见：当支撑外伸连接段具有较大的抗弯刚度时，在支撑受压过程中，约束单元在接触部位将产生切向摩擦力作用，该局部位置同时承受切向摩擦力及横向接触力，因此可将该部位看做一压弯构件（承受压弯作用效应），其控制截面为约束单元开槽位置的底部（全钢防屈曲支撑）或过渡段末端对应约束单元位置（钢管混凝土约束防屈曲支撑）；当压弯作用效应增大到该控制截面的极限状态后，约束单元对支撑端部的转动变形失去限制作用，支撑端部的转动变形将出现跳跃现象，最终支撑端部由于产生过大的转动变形而屈曲破坏。

图2 BRB外伸连接段失效模式1Fig.2 Failure mode 1 for the unrestrained connecting segment of BRB

当防屈曲支撑约束单元具有足够的强度和刚度时，往往可以避免失效模式1的出现。同样，在支撑受压过程中，伴随着端部产生转动变形，轴向力P也随之产生相应的附加偏心距，从而产生相应的附加弯矩作用，出现BRB外伸连接段破坏失效模式2，如图3所示。此时，可将支撑外伸连接段视为一压弯构件，即同时承受轴向力P与附加弯矩作用（压弯作用效应）。文献[27]对BRB外伸段的失稳破坏进行了试验和理论研究，结果表明：当压弯作用效应逐渐增大并达到外伸连接段控制截面的边缘纤维屈服应力时，支撑端部转动变形中将出现塑性变形成分，此时支撑根据塑性的发展程度仍可继续承受荷载，直至压弯作用效应增大至该控制截面的极限状态，进而失去继续承载的能力。

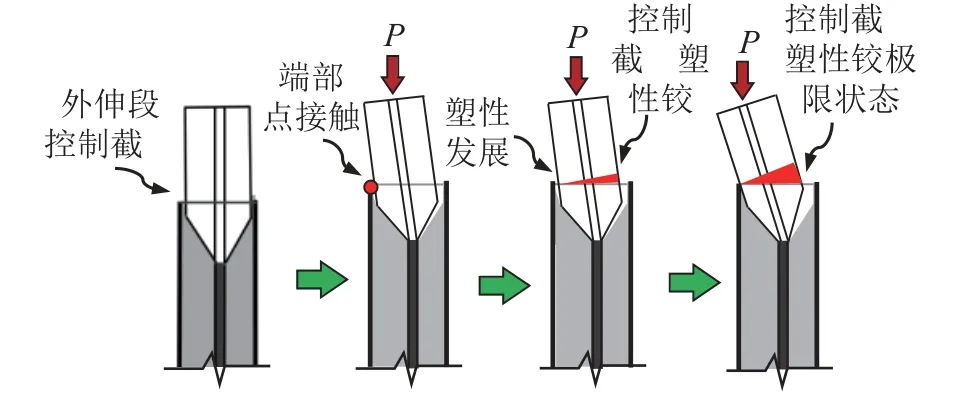
图3 BRB外伸连接段失效模式2Fig.3 Failure mode 2 for the unrestrained connecting segment of BRB

1.2 失稳破坏影响因素

1.2.1 失效模式1

通过对防屈曲支撑连接端部失效模式的分析容易看出，失效模式1是由于支撑端部转动产生的横向接触力Fh过大，致使约束构件失去对支撑端部转动的限制作用而失效，即横向接触力Fh的大小直接决定着失效模式1是否发生。外伸连接段失效模式1分析模型如图4所示。设支撑外伸连接段长度为Ll，过渡段长度为Lt，支撑端部发生转动前的简化计算模型如图4（a）所示。端部与约束构件间的横向接触力为Fh，约束单元控制截面处的弯矩为Mr；支撑在受压过程中时，接触部位还将产生切向的摩擦力Fµ，e为偏心距；文献[27]通过试验研究提出了BRB端部产生转动变形θ后的“两点接触”效应，如图4（b）所示。

图4 外伸连接段失效模式1分析模型Fig.4 Analysis model for failure mode 1 of unrestrained connecting segment

以支撑过渡段及外伸连接段为研究对象，对图4（b）中外伸段及过渡段列力平衡方程可得：

式中，c为核心耗能单元与约束单元间的间隙，µ为核心耗能单元与约束单元间的摩擦系数。

为分析外伸连接段长度及过渡段长度对横向接触力的影响，令

将式（2）代入式（1），得：

定义RF为横轴力比，即横向接触力Fh与轴向力P之比；定义Rc为间长比，即间隙c与L（连接段与过渡段长度之和）之比，即：

则式（3）可改写为：

在Rc不同取值下，根据式（5）绘制横轴力比RF与ξ间的关系曲线如图5所示。由图5可以看出：横向接触力Fh随ξ的增加呈非线性增大变化，即外伸连接段长度越长或过渡段长度越短时，Fh越大；当外伸连接段及过渡段长度确定时，Fh随Rc的增加而增大，即间隙c的取值越大，Fh越大；随着Rc取值的增加，RF的变化对外伸段长度和过渡段长度比例的改变更为敏感，也即对Fh的影响更为显著。从以上分析不难看出，当外伸段与过渡段长度比例设置不当（ξ取值较大），且间隙c的取值也较大时，Fh可达轴向力P的0.8倍左右，此时支撑较易出现失效模式1的破坏。由此可见，减小外伸段长度、增加过渡段长度及减小间隙c的取值，可提高支撑外伸连接段的稳定性。

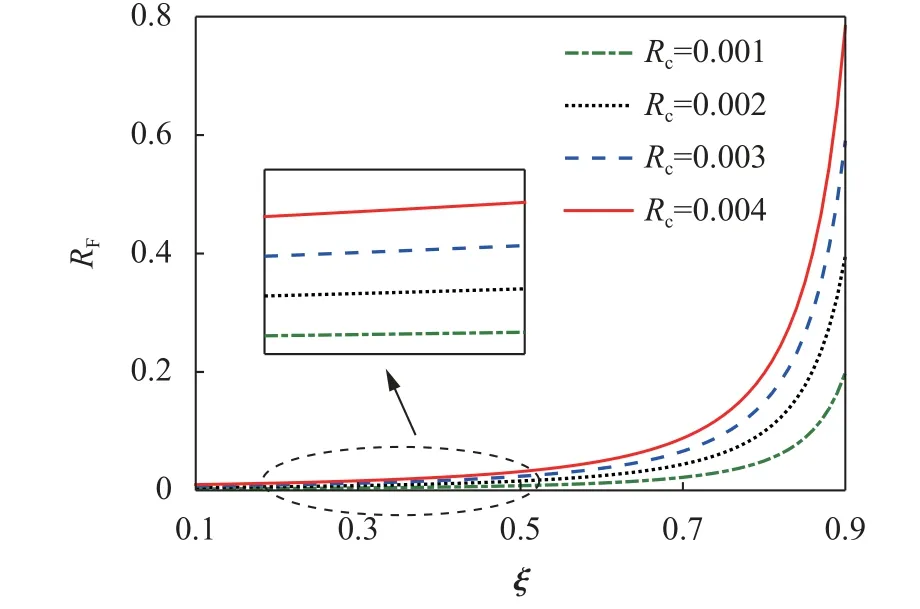
图5 横轴力比RF与 ξ关系曲线Fig.5 Relationship between the RF andξ

1.2.2 失效模式2

当失效模式1通过合理设计及合理构造被避免时，支撑端部的失效主要表现为外伸段底部控制截面出现可转动的塑性铰。此失效模式的主要原因是控制截面上的弯矩作用效应超过了该截面的极限承载力，因此控制截面上的弯矩大小是失效模式2的关键影响因素。以图4（b）中外伸连接段为研究对象，对连接段底截面列力矩平衡方程可得：

式中，Mcp为支撑外伸连接段底截面处的附加弯矩，θ为支撑外伸连接段转动变形后与竖直方向的夹角。

根据式（6），在间隙c不同取值下，BRB外伸连接段底控制截面附加弯矩Mcp与ξ的关系曲线如图6所示。

图6 外伸段控制截面弯矩Mcp与 ξ关系曲线Fig.6 Relationship between the Mcp andξ

由图6可以看出：附加弯矩Mcp随ξ的增加呈非线性增大，即外伸连接段越长或过渡段越短时，Mcp越大；当ξ的取值确定，即外伸段及过渡段长度确定时，Mcp随间隙c的增加而增大；随着间隙c的增大，外伸段和过渡段的比例对Mcp的影响越为显著。从以上分析可知，外伸段与过渡段的比例及间隙c的取值影响Mcp。当防屈曲支撑外围约束单元具有足够的强度和刚度时，即失效模式1被限制时，较大的外伸段、较小的过渡段及较大的间隙值对外伸连接段的稳定控制越为不利；反之，可提高支撑外伸连接段的稳定工作性能。

2 BRB外伸连接段改进构造形式

由防屈曲支撑外伸连接段失效模式及其影响因素的分析可知：1）加强端部约束单元刚度和强度以及采取相应措施减小横向接触力Fh均可有效避免失效模式1的出现；2）减小外伸连接段底截面处的附加弯矩Mcp有利于控制底截面处的压弯作用效应，即控制支撑在受压过程中产生的端部转动变形尽可能小，则可避免失效模式2的出现。基于此，本文提出如图7所示的改善外伸连接段稳定性能的端部构造形式，该构造形式将BRB中常见的无约束过渡段置于约束单元内部，在减小外伸连接段长度的同时增加过渡段的长度。设计制作3根端部改进后的全钢防屈曲支撑进行拟静力试验，以验证该端部构造形式的合理性及有效性。

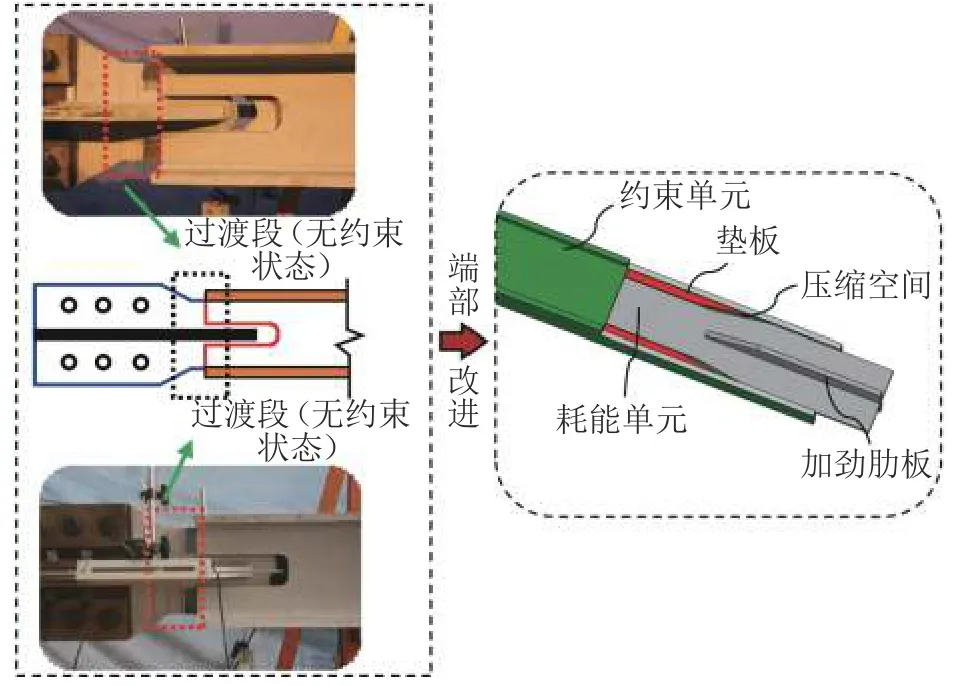
图7 BRB端部改进构造形式Fig.7 Improved construction form for the end of BRB

3 BRB外伸段稳定分析模型

失效模式1及失效模式2，均为压弯作用效应下相应控制截面处的内力超过其极限承载力的失效，如图8所示。

图8 失效模式1、2统一分析模型Fig.8 Unified stability analysis model for failure mode 1 and 2

文献[28]给出了压弯作用效应下基于边缘纤维屈服准则的稳定设计公式，两种失效模式下的外伸段稳定设计准则可采用式（7）进行统一表达。

式中，N为控制截面上的轴力，M为控制截面上的附加弯矩，Ap为控制截面的面积，Wp为控制截面的截面模量，fy为材料屈服强度。轴力N与附加弯矩M应分别对应BRB约束单元控制截面或外伸连接段控制截面上的内力进行取值，即N与M应分别针对失效模式1或失效模式2进行取值。根据图4及式（1）、（6）可得N及M为：

失效模式1：

失效模式2：

根据式（8）～（11）初步计算出控制截面上的压弯作用效应，并代入式（7）中；同时针对失效模式1及失效模式2验算是否满足相应的稳定设计条件。

4 BRB外伸段稳定性试验验证

4.1 试验设计

根据支撑端部改进后的构造形式，设计并制作3根满足式（7）稳定条件的全钢防屈曲支撑进行低周往复荷载试验，验证端部改进构造形式的合理性及稳定分析模型的有效性。3根试件材料均采用Q235钢，总长度相同，且耗能单元截面形式为“一”字型，如图9所示。3根试件的屈服承载力、弹性刚度及耗能单元宽厚比均不相同，各试件分别编号为ABRB1、ABRB2及ABRB3。

图9 端部改进后防屈曲支撑构造组成Fig.9 Composition of the BRB for end improvement

采用式（7）对失效模式1及失效模式2进行试件参数验算。验算过程中，摩擦系数µ取0.3，间隙c取1 mm，支撑轴向荷载P取1.5倍屈服承载力。各试件几何参数见表1。试件的低周往复加载制度采用位移控制的加载模式，以试件的总长度l为基准，分别为在l/800、l/600、l/300、l/200、l/150、l/100位移幅值下往复循环加载 3 次；此外，在l/80位移幅值下循环加载直至试件断裂破坏。

表1 试验试件几何参数Tab.1 Geometric parameters of specimensmm

4.2 测点布置

支撑端部转角变形通过布置在支撑弯曲变形平面内（弱轴平面）靠近加载端的2个位移计（D1、D2）进行量测，采用文献[27-28]中的转角测量计算方法进行计算，支撑端部转角变形测量及计算示意图如图10所示。由图10可知，将2个移计所测得的位移δl、δr的绝对值相加，除以2个位移计间的距离b，结果即为实测的支撑端部转角变形。因为支撑端部转动变形直接关系到外伸连接段的稳定性，因此，从测得的支撑端部转角变形量可初步判断外伸连接段在各级别荷载作用下的大致工作状态，从而评价其稳定工作性能。

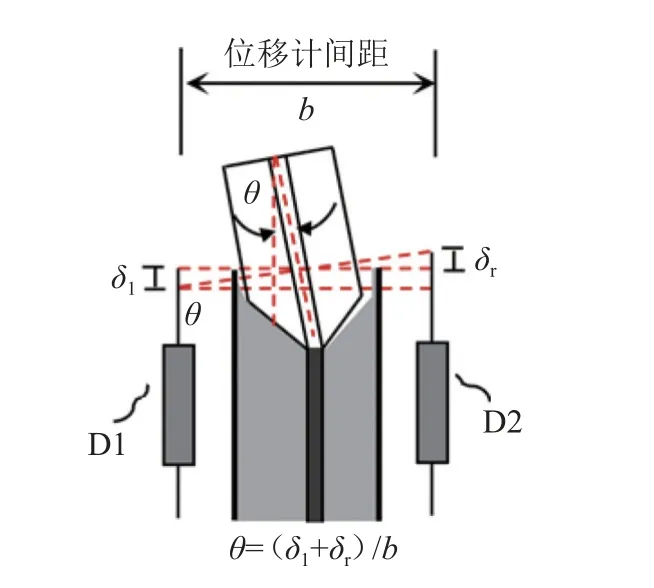
图10 支撑端部转角变形测量及计算[27-28]Fig.10 Measurement and calculation for rotational deformation at the end of BRB[27-28]

4.3 试验结果及分析

4.3.1 试验现象

3个试件的耗能单元在试验加载完毕后的屈曲变形形态如图11所示。由图11可以看出：各试件在轴向荷载作用下均出现了高阶多波屈曲模态，这是防屈曲支撑克服受压失稳获得较高受压稳定承载力的主要原因，同时也是引起支撑端部转动的一大因素；靠近支撑端部位置的屈曲波长较其他位置的屈曲波长更短，且屈曲幅值也更大，这是由于在轴向荷载作用下，核心单元与约束单元间的摩擦力所致，如图12所示。图12中，lw为曲波长，lwmin为屈曲波长最小值。整个试验过程中，3个试件外伸连接段均保持稳定工作状态，未出现失效模式1及失效模式2的失稳破坏现象，这在一定程度上验证了本文所提出端部改进构造形式的合理性以及稳定分析模型的有效性。

图11 加载完毕后试件耗能单元屈曲变形形态Fig.11 Buckling deformation morphology of core element of specimens after loading

图12 BRB屈曲波长分布Fig.12 Buckling wavelength distribution of BRB

图13为加载完毕后3个试件最终的破坏失效形态。由图13可见，试件ABRB1及ABRB2的约束单元在靠近支撑端部附近出现局部失稳现象，主要是由于摩擦力的存在，耗能单元产生高阶多波屈曲模态后，靠近支撑端部位置的屈曲幅值更大。在相同条件下，支撑端部附近位置更易出现局部失稳，因此，核心耗能单元也更易在该位置发生断裂破坏。试验中，3个试件核心耗能单元的断裂破坏位置均发生在支撑端部附近，且均为受拉过程中的断裂破坏。也即最终的破坏失效形式并非外伸连接段的失稳破坏，这也在一定程度上说明本文所提出端部改进构造形式合理可行。

图13 支撑失效破坏形态Fig.13 Failure modes of BRB

4.3.2 支撑端部转角变形分析

图14为3个试件在各级加载位移幅值处的实测转角变形与轴向荷载的关系曲线。图14中，轴向荷载用支撑各级加载首圈位移幅值处的实测轴向荷载P与屈服荷载Py的比值表征。

图14 支撑轴向荷载与转角变形关系Fig.14 Relationship between axial load and rotation deformation of BRB

由图14可以看出：支撑端部转角变形随着加载位移幅值的增加而增大，且3个试件的端部转角变形均处于很小的范围内，即支撑端部未出现明显的转动变形，这与观察到的试验现象相符；各试件转角变形曲线上有一较为明显的拐点，这主要是由于支撑在较大轴向荷载作用下将产生高阶多波屈曲的变形模态，此时支撑端部由于转动变形而产生附加弯矩作用，这种转动变形随着轴向荷载的增加不断增大。当支撑端部转动变形大于2倍间隙值c时，支撑端部将与约束单元产生点接触，两者相互接触后，转角变形虽然随着轴向荷载的增加继续进一步增大，但其抵抗转动变形的能力要强于接触前的自由转动状态。

4.3.3 支撑端部压弯作用效应分析

试验过程中，通过力传感器采集得到支撑两端的轴向荷载P，进而计算出支撑外伸连接段控制截面上的轴力N及附加弯矩M，得到外伸段控制截面上的压弯作用效应。为分析试验过程中支撑外伸段的实际工作状态，需分析其控制截面上的弹塑性承载力与实际压弯作用效应间的关系。采用文献[28-30]给出的方法计算控制截面纯压作用下的轴向塑性承载力Np与纯弯作用下的弯曲塑性承载力Mp，从而得到塑性承载能力关系曲线。

图15为3个试件在各级加载下，每一级最大加载位移幅值处的压弯作用效应N-M与支撑外伸连接段控制截面上的塑性承载力Np-Mp的关系。由图15可以看出，各试件在各级荷载作用下的压弯作用效应均分布在弹性区域范围内，表明支撑端部的转动变形很小，因而由该转动变形引起的支撑端部附加弯矩作用也较小。这与整个试验过程中各试件外伸连接段均未出现失稳破坏的试验现象相吻合，也在一定程度上说明本文提出的支撑端部稳定分析模型及改进构造措施能较为有效地保证支撑端部的工作性能稳定，并在一定程度上限制支撑端部产生过大的转动变形。