单层楼阁式木架动力与耗能性能试验研究

孙祚帅，贾良玖,2*，张宏泰，万 佳，项 平

(1.同济大学 土木工程学院，上海 200092；2.同济大学 土木工程防灾国家重点实验室，上海 200092；3.太原理工大学 土木工程学院，山西 太原 030024)

中国现存传统楼阁式木构较少，代表性建筑包括应县木塔和天津蓟县观音阁。日本的五重塔和三重塔也属于楼阁式木构，其建造技术在隋唐时期从中国传到日本。传统楼阁式木构经受了多次强震强风等自然灾害后依然保存下来，表明其具有独特而优越的防震机制。典型传统楼阁式木架可分为4层：柱基层、柱架层、铺作层和屋架层（附加质量层）[1]。柱通常浮搁于础石上，当受到较大的侧向力时，柱脚可绕础石滑动或提离；阑额和柱通过榫卯连接[2]，这些连接通常可滑动和摇摆，既不是刚性连接，也不是半刚性连接，连接的刚度和承载力通常比阑额和柱的刚度和承载力小[3-4]，允许梁和木柱在一定程度上转动和变形。连接构造使得楼阁式木架在地震时可通过柱摇摆、柱脚滑移和构件间的摩擦实现卓越的防震性能。同时，自重可提供恢复力，在一定位移和变形范围内实现结构自复位，从而使楼阁式木架具有一定的自复位特性。如今，受自然和人为因素等影响，中国传统楼阁式木构面临着许多保护和修缮问题亟待解决。

日本学者对五重塔的研究已持续一个世纪之久，且已建立了较为完善的五重塔、三重塔数据库。Chiba等[5]进行了古代五重塔的1/5缩尺模型振动台试验。Masaki等[6]对木架足尺模型进行了静力试验和振动台试验，指出木架恢复力主要由梁的抵抗弯矩和柱摇摆时的自重提供，同时证明了木架主要依靠重力自复位。国内对楼阁式木架的研究主要涉及木材材性[7]、榫卯连接[8]、斗栱铺作和整体木架[9]。王明谦等[10]为预测木材复杂的受力行为，建立了木材3维弹塑性损伤本构模型。基于燕尾榫试验研究，姚侃等[11]提出燕尾榫的最终破坏模式为榫头从榫眼中拔出，并给出了燕尾榫节点弯矩-转角关系理论计算公式。隋䶮等[12]对透榫和燕尾榫木架模型进行了水平低周反复加载，得到了透榫节点和燕尾榫节点滞回曲线，试验结果表明木架具有较好的变形能力。此外，薛建阳等[13]对有无填充墙板的穿斗式木架房屋进行了振动台试验研究。宋晓滨等[14]以7层传统楼阁式木塔为研究对象，对 1/5 缩尺模型进行了振动台试验，验证了木塔良好的抗震性能且发现木塔存在固接状态和摇摆状态的切换。姚侃等[15]在分析历史建筑柱基和柱连接形式与特点的基础上建立了柱脚滑动摩擦隔震模型，给出了柱脚滑移准则。Fang等[16]对木架动力特性进行了理论研究，为木架变形机理研究奠定了基础。Wan等[17]的研究丰富了木架摇摆理论，将木架变形划分为4个阶段，并利用有限元模型进行了验证。

Xiang等[18]受楼阁式木架摇摆响应启发进行的多重摇摆钢框架研究，将现代钢结构与古代木结构结合，阐明了多重摇摆钢框架机理和响应[19]。然而，楼阁式木架具有高度非线性，变形机制比单一的摇摆结构更为复杂[20]。目前，多数研究集中于对木架构件独立抗震性能研究，包括叉柱造斗栱节点竖向荷载受力试验研究[21]、宋式斗栱节点水平荷载试验研究[22]、斗栱节点滞回特性和滞回模型研究[23]、榫卯节点尺寸效应试验研究[24]、榫卯节点转动性能及滞回模型研究[25]、整体木架抗震试验研究[26]、整体木架抗震机理研究[27]及滞回性能研究[28]，并建立了木架损伤分析模[29]。当前针对具有4个结构层的楼阁式木架整体抗震性能研究较少且主要为分层独立研究，同时对各层的协调工作机制、动力及耗能性能未详细阐明，相关研究不能完全反映楼阁式木架整体性能。本文以典型3层木构楼阁为原型，在不考虑木材损伤情况下对单层1/16缩尺楼阁式木架进行了振动台试验；基于楼阁式木架地震力作用下的变形及运动状态理论分析结果[1]，研究单向地震激励下木架响应，并进一步分析木架的滞回曲线和累积耗能机理，为传统楼阁式木架抗震机理的研究提供理论和试验研究基础。

1 试验概况

原型结构为始建于公元984年的天津蓟县观音阁，高23 m，是一座3层木构楼阁，建筑尺寸参考文献[30]。其中：第1层与第3层为明层，除柱脚连接形式外，上部构造一致；第2层为暗层。第1层木架柱脚与柱基层为浮搁式连接，第3层木架柱脚与第2层铺作层为叉柱连接，第3层木架柱脚与下部结构连接形式与第2层木架一致。为了研究柱基层与柱架层复合抗震性能及浮搁式柱脚连接形式的工作机制，同时综合考虑振动台加载能力和台面尺寸，选择第1层明层对应的楼阁式木架中间跨为研究对象，设计并制作1/16的缩尺模型。缩尺模型相似比见表1。为了阐明这种复杂体系的动态响应，试件制作尽量与原型结构构造一致。鉴于小模型软木加工难度大，试件用材为核桃木（硬木），榫卯节点基本紧配。

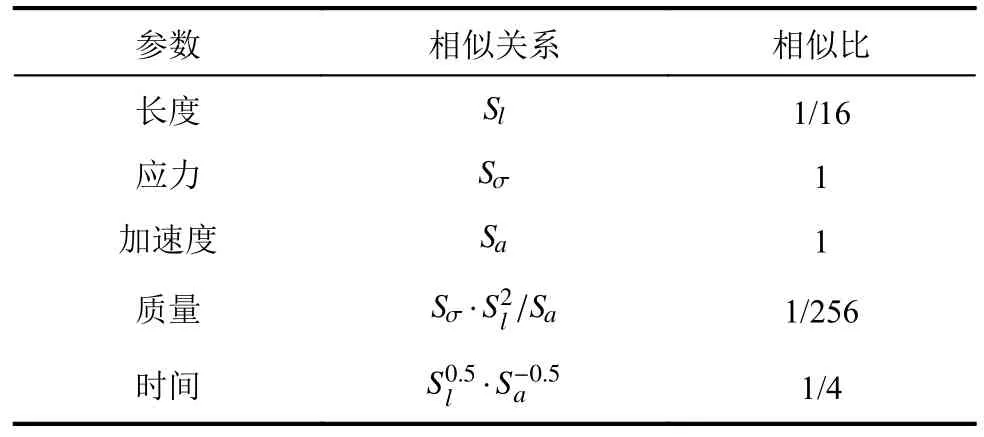
表1 缩尺模型相似比Tab.1 Similarity factors of scaled model

试件构造及试验布置如图1所示。由图1可见：铺作层和柱架层与原型结构构造一致；柱基层采用础石，础石材料为青石，尺寸为100 mm× 100 mm× 30 mm，保证试验过程中柱脚滑移不超过础石尺寸；柱础间摩擦系数为0.3。柱架层及上部重量采用附加配重布置，根据配重同木架质量比与原型结构质量比一致来计算配重，并将配重固定在铺作层上，柱架层承接铺作层与础石，阑额与柱为榫卯节点连接，柱脚浮搁于础石上，础石通过夹具固定在振动台台座上。

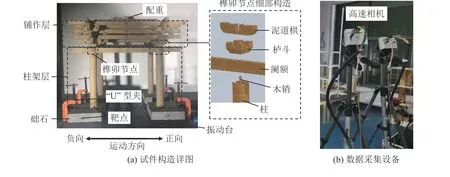
图1 试件构造及试验布置Fig.1 Overview of specimen structure and test setup

缩尺试件柱架层平面尺寸为255 mm× 180 mm，柱高222 mm，铺作层层高85 mm。由于木销作用，水平地震力下阑额只发生水平平动且与柱无相对水平位移，柱可绕榫卯节点转动，且榫卯节点最大正向转动角和最大负向转动角受试件加工精度影响有所不同。基于试验测试，试件正向柱架层层间位移角达到0.95%时榫卯节点卡住，负向达到1.13%时榫卯节点卡住。

选取PSL180波、CAP000波和FRN224波作为试验输入的单向地震动激励，地震波信息见表2，加载方向如图1（a）所示运动方向。

表2 输入地震波信息Tab.2 Summary of input ground motions

自由摇摆的刚体的频率与响应的位移振幅有关，位移导致频率的巨大变化，故选取3条具有不同卓越周期的地震波阐明这复杂体系的动态响应。由于本文进行的是楼阁式木架原理性试验，为保证缩尺模型与原型结构非线性地震响应相似性，试件缩尺比对地震波时间按照1/4进行缩尺。分别调整地震动峰值加速度（PGA）至0.07g、0.20g和0.40g对应小、中、大震；将PSL180波PGA调幅至0.60g的工况进一步研究试件响应。3条地震波加速度反应谱及平均值与规范谱的对比如图2所示。

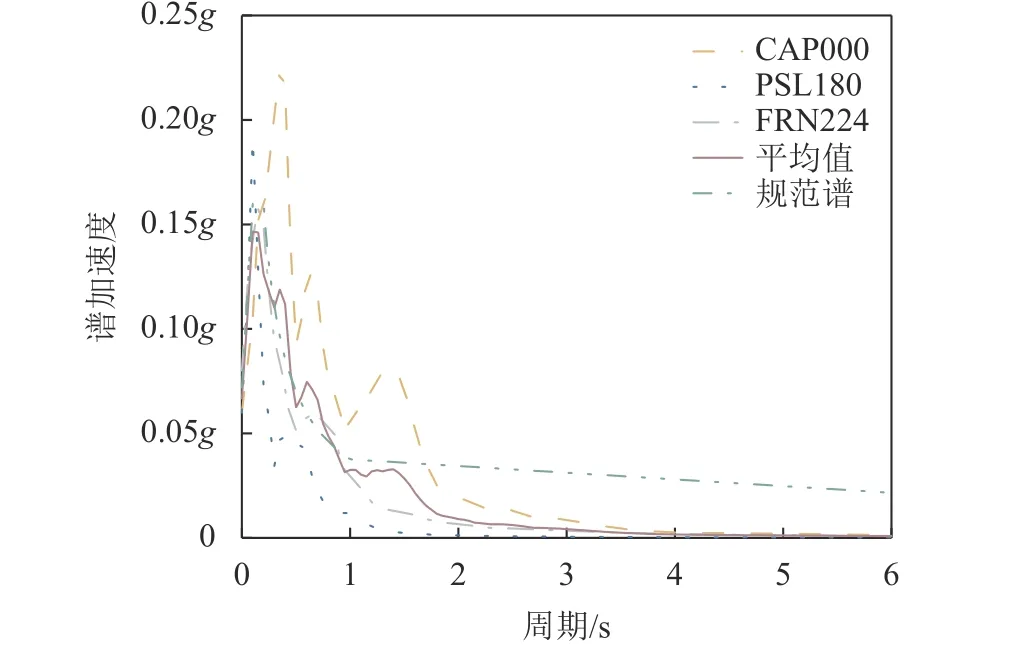
图2 地震波加速度反应谱Fig.2 Acceleration response spectrum of seismic waves

每次地震波加载前需保证试件初始位置一致，利用水平尺校准柱与础石垂直且加载方向上每2根柱在同一平面内，并在础石上做出位置标记。在关键位置布置靶点并利用图1（b）所示的高速相机进行靶点跟踪，即通过DIC（Digital Image Correlation）进行数据采集，设置相机采集频率为100 Hz，可获取靶点处位移及加速度等数据。

2 试验结果及分析

2.1 试验现象

Sun等[1]提出柱摇摆、柱脚滑移和柱脚提离等运动状态的判别公式为：

式中：ax为阑额水平加速度；g为重力加速度；α为柱重心和柱脚边缘连线与柱轴线夹角；µ为柱底与础石间的静摩擦系数，通过摩擦角法得到实测值为0.3；S为柱脚抬起高度；B为柱半径；2H为柱高。分析坐标系是以振动台为参考基点的非惯性系。

输入PSL180波、CAP000波和FRN224波，试验木架均出现了柱摇摆、柱脚滑移和柱脚提离等关键运动状态，且均适用于判别式（1）～（3）；同时，3条地震波定性分析结果一致，因此在考虑试验加载工况后，以PSL180地震波为例进行阐述。PSL180地震波激励时，0.07g工况下，整个时程内试件响应较小，式（1）～（3）均不满足，柱无法起摆的同时不产生柱脚滑移且无柱脚提离；0.20g工况下，部分时刻地震响应满足式（1），发生柱摇摆，但在峰值加速度时刻不满足式（2），因此无柱脚滑移；0.40g工况下，同时满足式（1）和（2），柱可摇摆且柱脚产生滑移，柱脚滑移现象如图3（a）所示；进一步分析0.60g工况下，试件出现柱摇摆、柱脚滑移和柱脚提离现象，柱脚提离现象如图3（b）所示，即整体木架摇摆。

图3 试验现象Fig.3 Test phenomenon

PSL180地震波0.60g工况下的试件加速度响应和层间位移角响应如图4所示，多个时刻的加速度响应满足式（1）和（2），即可产生柱摇摆和柱脚滑移，同时在峰值加速度附近满足式（3）。图4中，θlim为榫卯卡住时木架层间位移角。同样以PSL180为例进行分析：当PGA≤0.40g时，榫卯节点不会卡住，也不会产生柱脚提离现象；当PGA达到0.60g时，层间位移角达到榫卯节点卡住条件后出现柱脚提离现象。榫卯节点卡住前，发生柱摇摆；榫卯节点卡住后，发生木架摇摆，即受拉侧柱脚提离。当水平地震力较大时，柱摇摆位移对应的摇摆角达到榫卯节点间隙容许值，水平地震力再增大后不再产生柱摇摆位移，此时判定榫卯节点已卡住。榫卯节点是否卡住是判别柱脚提离现象的关键，当榫卯节点卡住且满足式（3）时，才会出现木架受拉侧柱脚提离现象。图4（a）中有3个典型时间点满足式（3），对应于图4（b）位移响应时，正向2个时间点满足式（3）且满足榫卯节点卡住的条件，因此位移正向时产生柱脚提离；负向1个时间点满足式（3）但并不满足榫卯节点卡住的条件，因此位移负向时不产生柱脚提离。

图4 PSL180地震波PGA 0.60g工况响应Fig.4 Response under seismic excitation PSL180 with PGA of 0.60g

2.2 位移响应分析

3条地震波作用下木架铺作层与柱架层层间位移数据见表3，其中，柱架层层间位移为阑额水平位移与柱脚水平位移的差值，铺作层层间位移为顶梁水平位移与阑额水平位移的差值。由表3可知，地震作用下，铺作层层间位移较小，柱架层层间位移较大，且随着РGA增大，铺作层层间位移占比减小，柱架层层间位移占比增大。试验结果表明，木架水平位移主要由柱架层贡献，因此本文仅分析柱架层的位移响应。РSL180地震波激励下不同РGA的对应柱架层层间位移角及对应最大层间位移角贡献如图5所示。

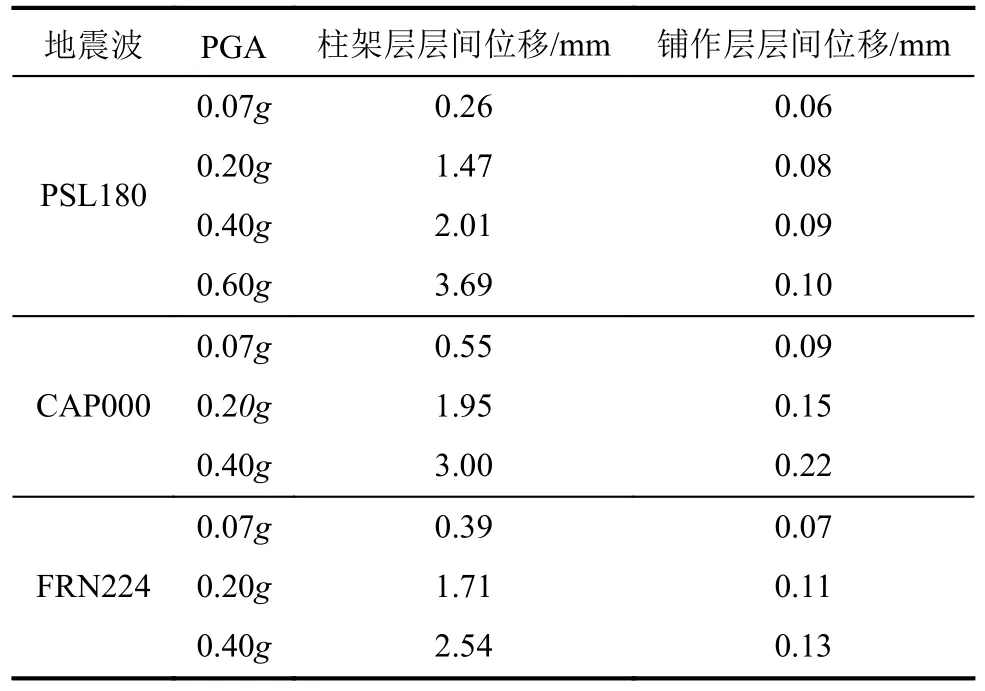
表3 输入3条地震波作用下木架位移响应Tab.3 Displacement response of timber frame under 3 input seismic waves

图5 PSL180波不同PGA对应位移响应Fig.5 Displacement response under seismic excitation PSL180 with different PGAs

由图5可见：РGA为0.60g时，最大层间位移角主要由柱摇摆贡献，占比60%，柱脚提离贡献占比40%。试验中，正向柱架层层间位移角达到0.95%时榫卯节点卡住，负向达到1.13%时榫卯节点卡住。榫卯节点卡住前发生柱摇摆，一旦榫卯节点卡住，柱摇摆不再发生。由试验结果可知，在不考虑材料塑性的前提下，柱摇摆和柱脚提离是中、大震下楼阁式木架位移响应的主要模式，且榫卯节点卡住与否是楼阁式木架状态切换的关键影响因素。

2.3 滞回曲线

РSL180地震波激励下不同工况柱架层滞回曲线如图6所示。图6中：横坐标为柱架层层间位移角，定义为阑额绝对位移-柱脚绝对位移间的差值与柱高的比值；纵坐标为阑额处水平地震力Fe=max，其中，m为楼层质量。由图6可见：输入激励较大的0.40g和0.60g工况下，滞回曲线饱满；输入激励较小的0.07g和0.20g工况下，滞回曲线包围面积较小。РGA为0.07g时，试件响应较小，滞回曲线近似表现为线弹性曲线；РGA为0.20g和0.40g时，出现柱摇摆，滞回曲线包络线近似为双线性，柱摇摆后表现为减小的2阶刚度；РGA为0.60g时，柱摇摆和柱脚提离会相继发生，大层间位移角下滞回曲线包络线表现为柱脚提离后的负刚度。

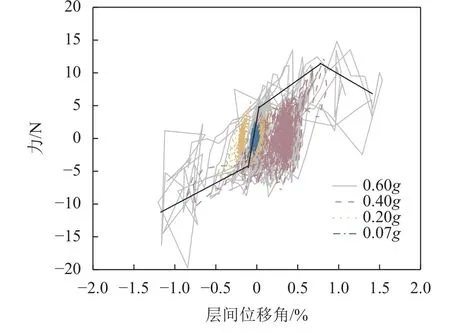
图6 PSL180波不同PGA对应柱架层滞回曲线Fig.6 Hysteretic curves of timber frame under seismic excitation PSL180 with different PGAs

根据0.60g工况的黑色骨架曲线线形，计算3段刚度k1、k2、k3，结果见表4。由表4可知：2阶刚度k2约为初始刚度k1的18%；柱脚提离后，滞回曲线呈现负刚度k3，约为初始刚度k1的20%。

表4 PSL180地震波不同PGA对应结构刚度值Tab.4 Structural stiffness under seismic excitation PSL-180 with different PGAs N·mm-1

柱脚提离后柱架层层间位移角、阑额水平地震力和柱脚提离高度如图7所示。阴影部分表明柱脚提离后，柱架层层间位移角增大，水平地震力减小，对应滞回曲线的负刚度段。

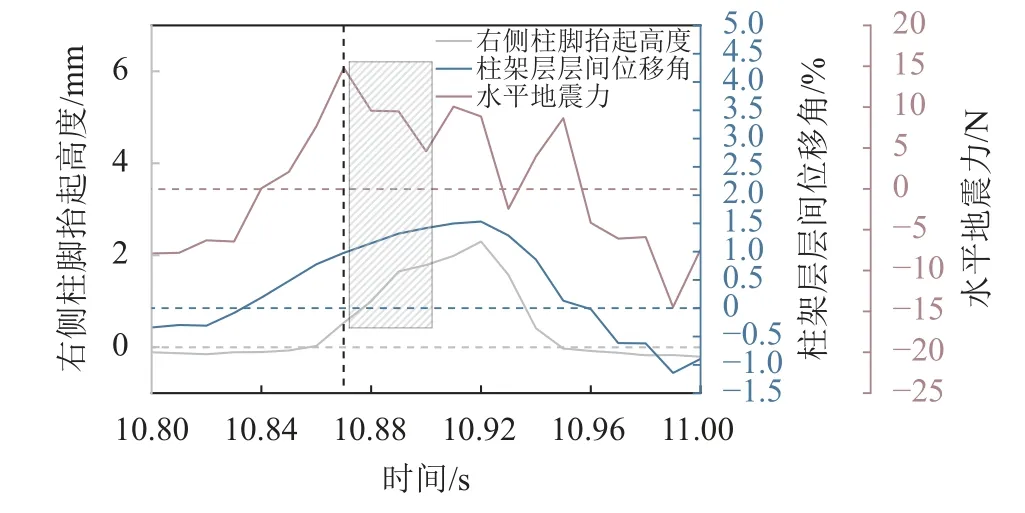
图7 柱脚提离后柱架层响应Fig.7 Response of timber frame after column uplifting

2.4 累积耗能

滞回曲线面积表示试件累积耗能量，按试件各部分滞回曲线面积计算PSL180地震波各工况累积耗能时程，分析试件各部分累积耗能如图8所示。图8中，柱架层摇摆及榫卯节点摩擦耗能、铺作层构件抬落及摩擦耗能和柱脚滑移耗能为3个耗能机制。

图8 PSL180波不同PGA对应各部分累积耗能Fig.8 Cumulative energy dissipation of components under seismic excitation PSL180 with different PGAs

由图8可见，随PGA增大，各部分累积耗能增大，试件总累积耗能增大。PGA为0.07g和0.20g时，未发生柱脚滑移，柱脚滑移累积耗能近似为0；PGA为0.40g和0.60g时，发生了柱脚滑移，且柱脚滑移耗能占比最大，见表5。进一步分析柱架层和铺作层累积耗能：0.07g工况下试件响应小，理论上不会产生各种非线性响应，累积耗能近似为0，而实际柱底不平整也会导致在较小地震动下柱架层产生位移；0.20g工况下，柱架层仅在部分加速度较大时刻发生柱摇摆，并伴随榫卯节点组件间的摩擦及相对转动，而铺作层通过斗栱各构件间的摩擦及复位行为耗能，铺作层累积耗能大于柱架层累积耗能，且铺作层耗能占比最大；0.40g和0.60g工况下，柱架层摇摆、榫卯摩擦及柱脚提离等非线性响应导致柱架层累积耗能大于铺作层累积耗能，且当PGA≥0.40g时，PGA越大，柱架层累积耗能占比越大，铺作层累积耗能占比越小。

表5 不同PGA地震波作用下各部分累积耗能及占比Tab.5 Cumulative energy dissipation and proportion of energy dissipation of components under input seismic waves with different PGAs

3 结 论

1）本文通过缩尺振动台试验研究了楼阁式木架的非线性动力响应及耗能性能。随输入地震波加速度增大，楼阁式木架会发生柱摇摆、柱脚滑移和柱脚提离等非线性响应；在不考虑结构自身变形的情况下，榫卯节点卡住前，柱架层层间位移由柱摇摆模式控制，榫卯节点卡住后，柱架层层间位移由柱摇摆和柱脚提离两种模式共同控制。

2）柱摇摆前，滞回曲线包络线呈现较大初始刚度；柱摇摆后，滞回曲线包络线呈现2阶刚度，且2阶刚度约为初始刚度的18%；柱脚提离后，滞回曲线呈现负刚度，约为初始刚度的20%。

3）当РGA≤0.20g时，楼阁式木架各部分累积耗能较小，框架响应较小；当РGA≥0.40g时，柱摇摆、柱脚滑移和柱脚提离等非线性响应明显，柱脚摩擦滑移成为最主要的耗能形式；РGA越大，柱架层耗能占比越大，铺作层耗能占比越小。

由于试验中质量缩比导致木材未发生塑性变形，后续将进一步开展大型振动台试验，深入研究缩比效应以及多层楼阁式木架的减隔震机理，为中国传统楼阁式木架古建的保护、修缮以及重建提供技术依据。