基于同步时频特征分析的配电网接地故障定位方法
2023-10-12高朋高宏宇王岩高扬乔建
高朋, 高宏宇, 王岩, 高扬, 乔建
(1.东北电力大学 电气工程学院,吉林 吉林 132012;2.国网吉林供电公司,吉林 吉林 132001)
0 引 言
小电流接地系统中,发生单相接地故障后,故障特征不显著,导致故障检测准确度低。由于暂态量含有的信息丰富,比稳态量具有更大的优势。文献[1]通过暂态信号功率方向比较原理构造定位判据。文献[2]指出故障点两侧暂态电流极性不存在明显特征,因此基于极性特征实际使用效果并不好。折射波和反射波的存在使得行波法[3]检测复杂化,现场应用中还需要进一步验证。文献[4]利用小波提取故障特征量,但方法依赖小波基函数的选取,抗干扰能力差。文献[5]提取首容性频段内的信号用于后续算法的使用。随着目前信息采集技术的发展,广域同步测量系统在配电网中得到了有效的利用,通过同步相量测量装置获得同步低延迟和高分辨率的测量数据,给定位技术的发展带来了契机。借助同步相量测量装置,本文利用广义S变换进行时频分析,提出故障区段识别的新方法。
1 零序网络阻抗特性分析
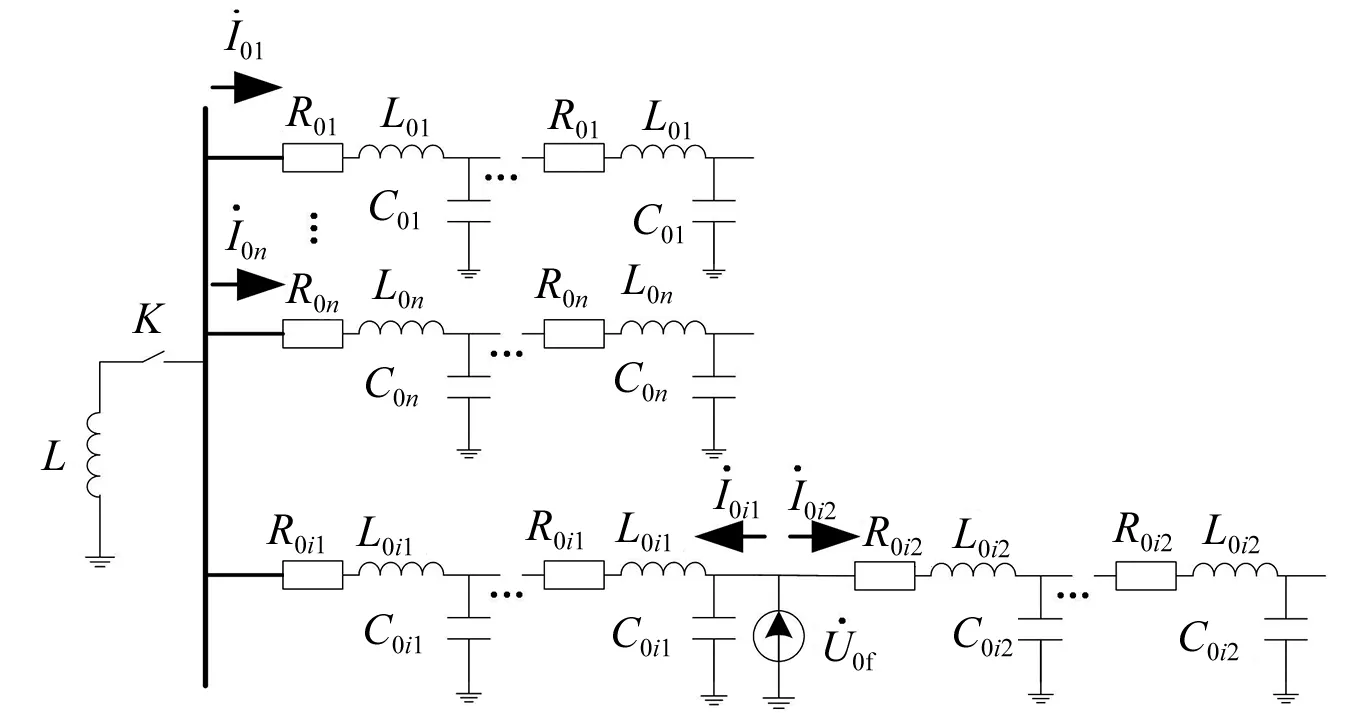
图1 系统零序网络拓扑
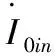
对于单条健全线路来说,线路k始端的输入零序阻抗为:
(1)
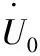
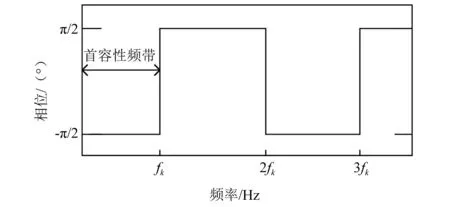
图2 线路k的相频特性
线路k首次发生串联谐振的频率fk[6]为:
(2)
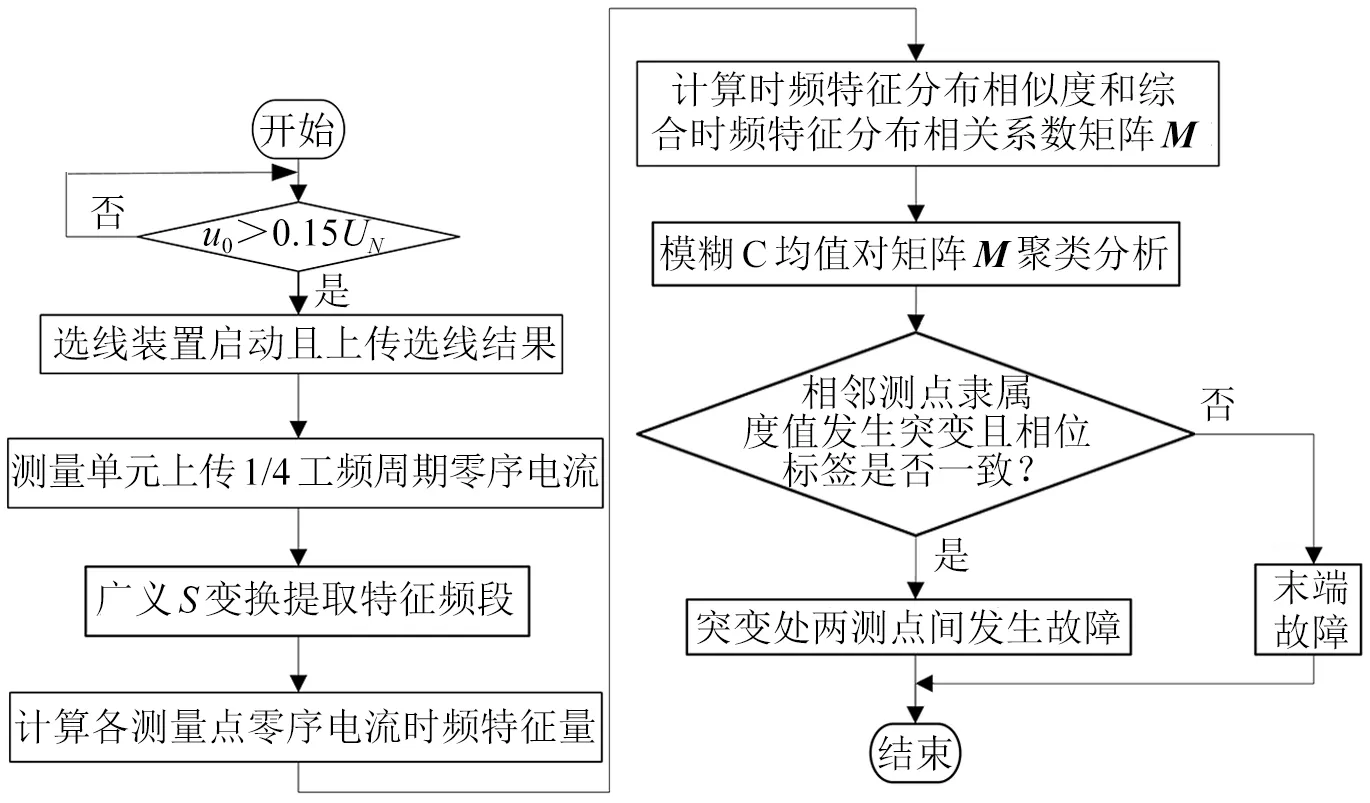
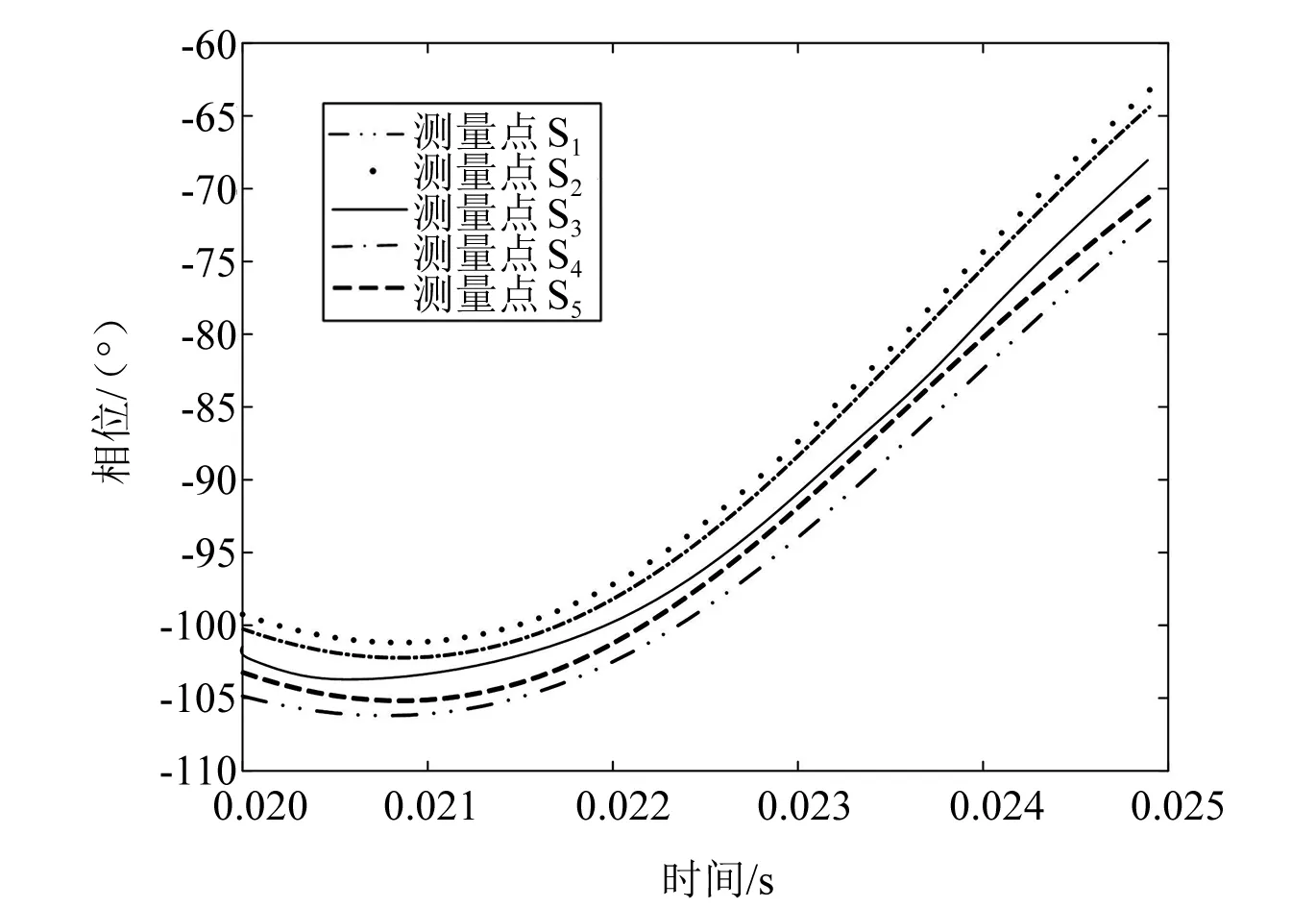
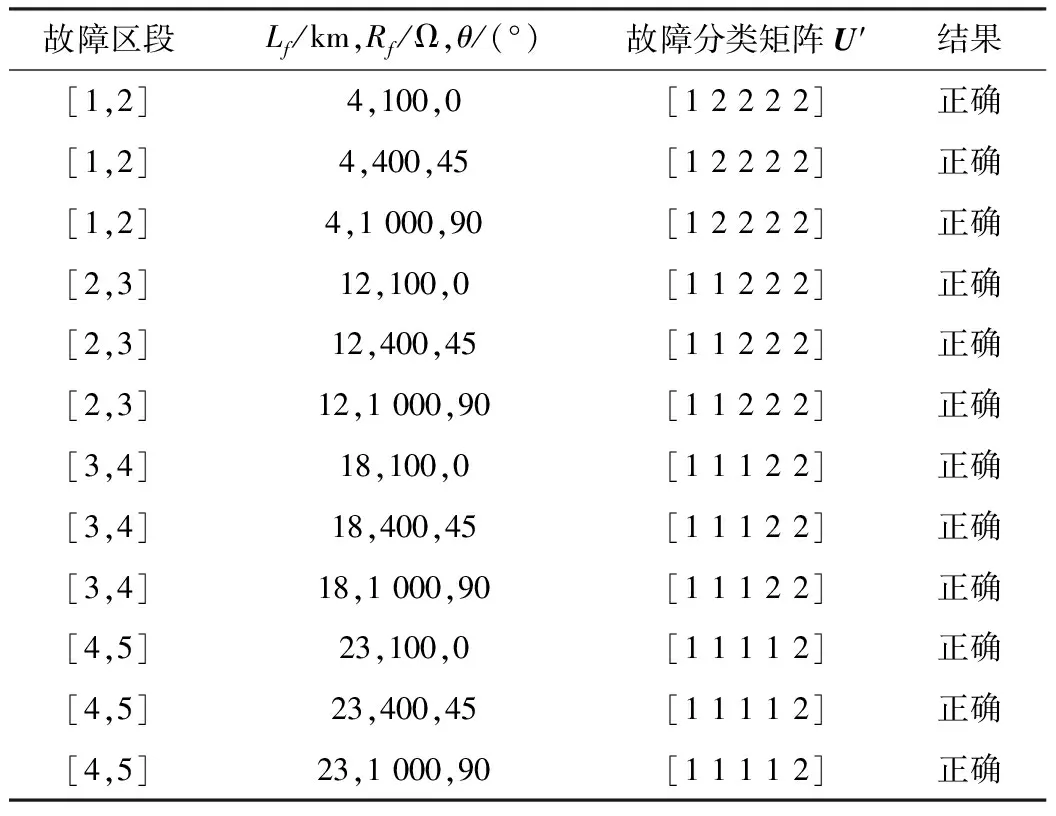
对于谐振接地网络,在f′ 零序电流信号x(t)广义S变换[8]的离散结构可表示为: (3) 经过处理后得到复时频矩阵S[p,q],该矩阵由复数元素构成,矩阵的每一行元素表示某一频率下信号的时域分布特性,每一列元素表示某一时间下信号的幅频分布特性。 由第1节所述,求得针对某一谐振接地系统的特征频段范围,将零序电流信号经式(3)处理后,得到矩阵S[p,q]。假设矩阵S[p,q]的第i行到第j行表示特征频段,那么定义S[p,q]第k行对应的幅值为: (4) 式中:abs(·)为求模运算;N为采样数据的长度,同时也是矩阵的列数;k∈[i,j]。现定义故障线路第R个测量点在特征频段内的暂态零序电流时频特征量为: FR=[Ai,Ai+1,…Ak,…,Aj] (5) 为了衡量相同数据窗内信号的时频分布特征,定义故障出线测量点R和测量点L的时频特征分布相关系数为: (6) 式中:FR、FL分别为测量点R和L的暂态零序电流时频特征量;COV(·)为协方差;D(·)为方差。相关系数的取值大小反映了信号之间的相似程度。 考虑到发生弱故障时,由于暂态高频分量小、信号衰减快,可能导致频段内不同检测点之间的相关系数值差别小,因此借助时频能量的观点对式(6)进行改进,把改进后的定义为时频特征分布相似度,见式(7)。 (7) 式中:E(FR)、E(FL)分别为FR、FL的数学期望。 为便于比较不同测量点之间时频特征的关联程度,提高对故障判别的可信度,同时将故障特征最大化,定义任一测量点i的综合时频特征分布相关系数为: (8) 模糊C均值聚类通过迭代修正使样本空间中样本数据对某一聚类中心的隶属度加权距离和最小化,进而实现柔性聚类划分。利用模糊C均值聚类将故障线路所有测量点构成的综合时频特征分布相关系数矩阵M分成两类,即故障与非故障,使得聚类损失函数最小。聚类损失函数表示为: (9) 最终获得2×l阶最优模糊隶属度矩阵U,l为故障出线测量点的数目。行表示两个类别,列对应各个测量点,矩阵中的元素表示测量点到聚类中心的隶属度。 末端故障时,接地处只有一个测量点,采用前述方法会出现误判。为了提高算法的适用性,结合第1节的内容,特征频段内零序电流的相位是相反的。利用式(3)得到的矩阵对相应的特征频段进行重构,后对其求相角运算,则第i个测量点在特征频段[e,g]内相位随时间变化的曲线为: (10) 式中:N为采样点长度。 特征频段内故障点两侧零序电流相位反向,那么对应着的相位变化曲线一定是:一条曲线值都为正,另一条曲线值都为负。则第i个测量点相位离散序列Phi=[θ1,θ2,…,θN]。 图3 定位流程图 图4为MATLAB仿真软件搭建的10 kV谐振接地系统的简化模型。图4中:L1-1~L4的长度分别为6 km、14 km、12 km、16 km、32 km;S1~S5为数据同步测量装置。系统的补偿度为10%,采样频率为10 kHz。线路单位长度参数为R1=0.096 Ω、L1=1.22 mH、C1=0.011 μF、R0=0.23 Ω、L0=3.66 mH、C0=0.007 μF。 图4 配电网仿真模型 图4所示网络特征频段范围为150 Hz~1 000 Hz,对应着复数矩阵中的第3行到第21行。设0.02 s时出线L4A相经200 Ω电阻接地,故障点f1距离母线18 km,故障初相角为90°。仿真得到故障出线各测量点的暂态零序电流,如图5所示。 图5 各测量点零序电流 利用式(3)进行处理,可以得到各测量点信号在特征频段内的复数矩阵,计算特征频段内各测量点之间的时频特征分布相似度,得到由全部测量点组成的综合时频特征分布相关系数矩阵M。 (11) 经过模糊C均值聚类之后得到隶属度矩阵U。 (12) 隶属度值在第3列与第4列间发生突变,说明故障点在测量点S3和S4之间。为更清晰看出故障点所在位置,对隶属度矩阵进行简化,将没有发生数值突变前的所有测量点分别记为1,将发生数值突变后的所有测量点分别记为2,得到故障分类矩阵为: (13) 当线路L4末端发生故障,故障初相角为90°,过渡电阻为800 Ω,通过模糊C均值聚类得到的隶属度矩阵为: (14) 此时分类错误,通过式(3)得到的复数矩阵在特征频段内进行重构,后取相角运算,得到各测量点在特征频段内相位随时间变化曲线,如图6所示。 图6 各测量点相位变化曲线 从图6可知,各测量点的相位都为负值,那么S1~S5测量点的相位标签记为Ph=[2 2 2 2 2],以此推断线路末端发生故障。不同故障情况下故障定位结果如表1所示。 表1 典型故障区段定位结果 本文提出了一种基于时频特征分析的配电网区段定位方案。在零序网络特征频段基础上,利用广义S变换对特定频段数据窗进行时频分析,从时域和频域的角度,揭示了故障点上游和下游在该数据窗内时频特征和相位差异,综合判据的使用大大提高了故障检测的准确度。经仿真验证,该方法能够准确地定位出故障点所在区段,克服末端故障的死区问题,且该方法抗弱故障能力强,故障识别准确度高。2 基于时频特征分析的区段定位
2.1 广义S变换
2.2 特征量时频特征分析
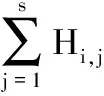
2.3 模糊C均值聚类实现区段定位
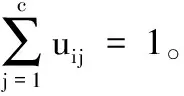
3 线路末端故障分析
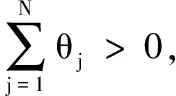
4 算例分析
4.1 仿真模型

4.2 仿真分析

5 结束语
