考虑广域行波信号强噪声干扰的输电线路故障定位
2023-10-12黄南天刘洋蔡国伟
黄南天, 刘洋, 蔡国伟
〔现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学),吉林 吉林 132000〕
0 引 言
准确定位输电网故障位置,可以有效减少停电时间,避免不必要的经济损失[1-2]。目前常用的故障定位方法有行波法和阻抗法。其中,行波法的故障测距精度高,不受过渡电阻和故障类型等因素的影响,在工程实践中得到了广泛的应用[3-4]。为了抑制行波噪声,文献[5]采用S变换提取行波首波头高频分量累加值作为定位判断依据,并利用小波Teager能量算子精确测距。文献[6]利用小波变换对行波进行处理,该方法具有较好的局部特性,抗噪声性能较好,但面对不同采样率与数据窗口,自适应性较差。上述方法对噪声的抑制起到了较好的效果,但缺少对各测点噪声数据的联合分析,忽略了测点间量测数据的时-空关联特性。
针对上述分析,提出了一种考虑行波测点强噪声数据干扰的输电网故障定位方法,从时间及空间耦合角度对各节点故障时段数据进行多级去噪。从而降低量测数据中噪声信息对故障定位精度的影响。在此基础上。利用时-空图卷积网络(spatial-temporal graph convolutional network, S-TGCN)及故障时段各测点行波信号构成的图数据,建立考虑输电网全局特征感知的故障定位模型。
1 行波信号时-空多级去噪
1.1 行波信号时-空基础去噪
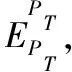
(1)
对EpT中的所有序列分别进行1-D离散余弦变换,然后对变换后的子序列矩阵进行2D离散小波变换,获得估计的相似子序列集合的稀疏表示ZpT。即:
ZpT=T-1F-1{R{F[T(EpT)],η·λth2D}}
(2)
式中:T为1-D离散余弦变换算子;F为2-D酉变换算子;λth2D为阈值参数;R为硬阈值滤波算子。对于中心位于pT的目标子序列获取其估计权重ωpT,即:
(3)
式中:Nht为硬阈值滤波后非零的变换系数数量。估计权重ωpT和补偿权重ωA(pm)用于聚合所有估计的相似子序列。基础去噪结果zht(pi)由加权聚合得到,即
(4)
式中:pm为相似子序列集合EpT中的采样点;χpm为中心位于pm的子序列对应的同尺寸特征函数。
1.2 行波信号最终去噪
行波信号最终去噪的流程与基础去噪大致相同,区别在于:最终去噪通过式(5)计算子序列匹配的相似度距离d,用维纳滤波器代替硬阈值滤波器,利用式(6)计算维纳滤波算子WpT,通过式(7)获得相应的估计权重ωpT。
(5)
(6)
(7)
2 广域行波信号和S-TGCN相结合的故障定位方法
为充分挖掘故障位置与各测点行波特征间的非线性映射关系,构建广域行波信号与S-TGCN相结合的故障定位总体架构如图1所示。
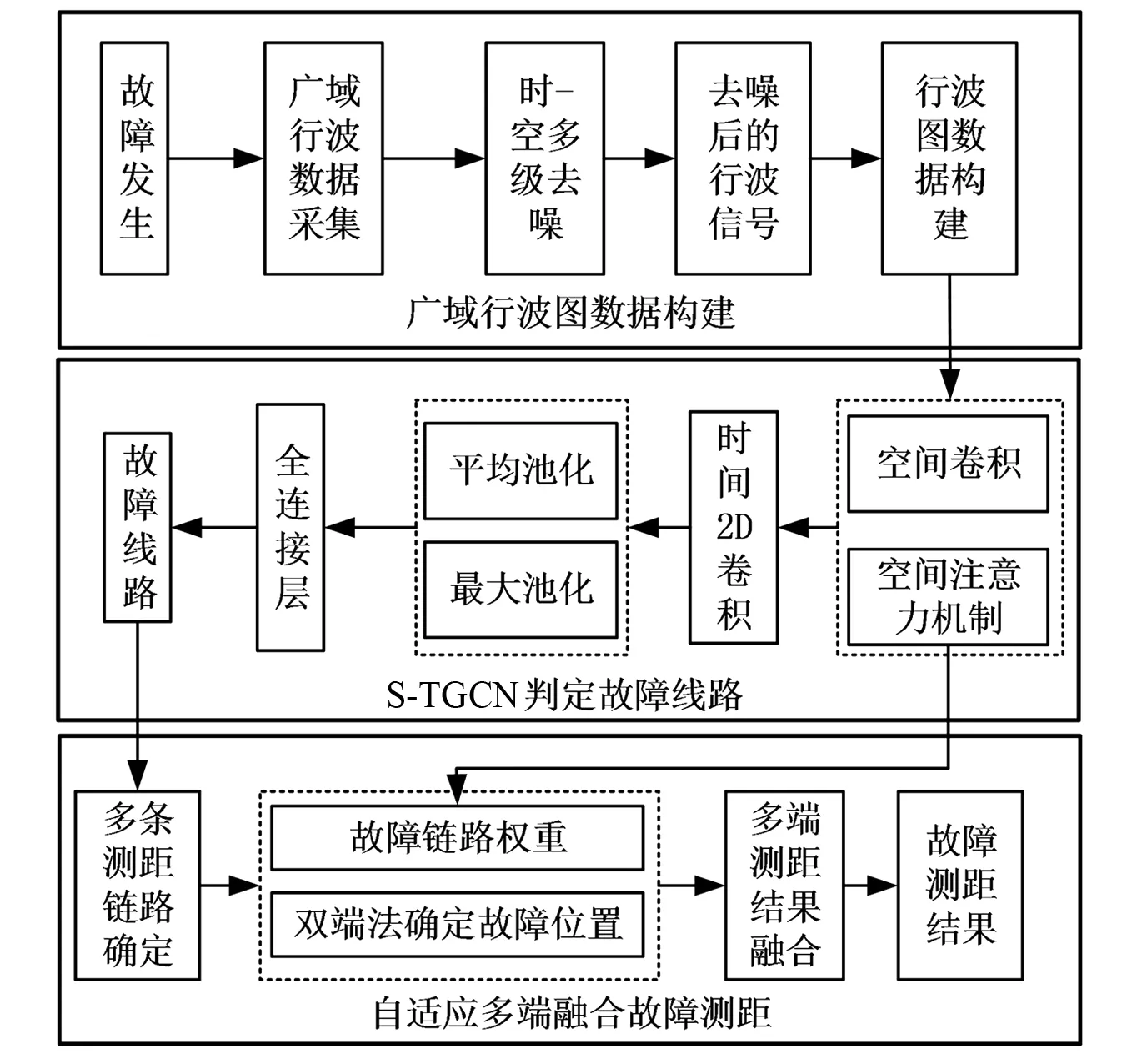
图1 S-TGCN故障定位总体架构
2.1 广域行波图数据构建
设输电网行波测点安装在母线处。广域行波图数据由两部分组成,一部分为反应各母线联结关系的邻接矩阵A,另一部分为去噪后各母线电压的行波线模量矩阵X={x1,x2,…,xN}。
(8)
式中:i,j∈{1,2,…,N}。若i节点与j节点直接相连时,ai,j=1,否则为0。对于任意节点xi,采用波头最先到达的测点为基准,截取各母线行波到达前0.05 ms和到达后0.95 ms内的三相电压,采样率为1 MHz,并通过凯伦贝尔变换获得行波线模量。
2.2 S-TGCN判定故障线路
采用S-TGCN对广域行波图数据进行特征提取及故障线路识别。首先利用时-空图卷积层对输电网全局时-空故障特征进行提取,然后通过全连接层输出故障线路。其中,空间注意力机制会得到各节点的自适应权重,参与到故障测距计算中。时-空图卷积由空间图卷积和标准时间卷积组成。
采用基于谱的图卷积运算提取输电网各测点行波空间维度上的空间特征。基于K-1阶切比雪夫图卷积的定义为:
(9)
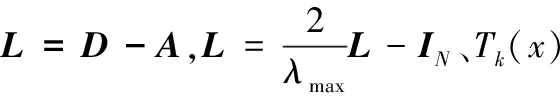
利用一个标准的2D卷积层来提取时间特征。第l层上的时域卷积运算定义为:
X(l)=ReLU{Φ*[ReLU(gθ*GX(l-1))]}
(10)
式中:ReLU为激活函数;Φ为卷积核的参数;*为标准卷积运算。
空间注意力机制通过空间注意力矩阵参与图卷积层的运算。空间注意机制定义如下:
P=Vp·σ[(X(l-1)Z1)Z2(Z3X(l-1))T+bp]
(11)
式中:Vp、bp、Z1、Z2、Z3为模型的可训练参数;σ为sigmoid激活函数;X(l-1)为第l层的输入,X(l-1)=(X1,X2,…,XTl-1)∈RN×Cl-1×Tl-1;P为空间注意力矩阵。
2.3 自适应多端融合故障测距
为确定故障点的具体位置,根据故障线路构成多条测距链路,借助空间注意力机制输出的自应权重融合多条链路的测距结果,提高测距精度。具体步骤如下。
(1) 对各测点行波信号的线模量xi(t)引入Teager能量算子进而准确确定首波到达时刻:
(12)
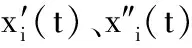
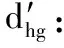
(13)
式中:c为行波线模波速;lgh为测点h到g之间的电气距离。
(3) 计算任意i-j链路的权重Wi,j,多链路的测距结果加权平均求取最终故障测距结果dp。
(14)
3 仿真验证
3.1 仿真介绍
在PSCAD/EMTDC中搭建图2所示电压等级为220 kV的输电网。输电线路采用频率相关相域模型。输电线路的长度如图2所示,单位为km。每个母线上安装行波信号测点。
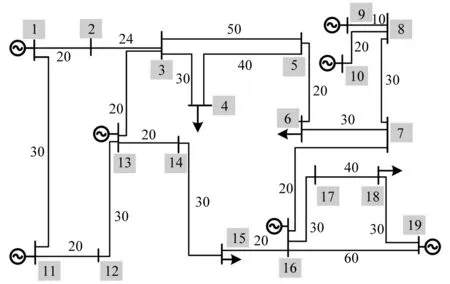
图2 仿真系统图
对每条线路模拟144次单相接地故障,故障位置在线路上均匀分布。故障初相角δ为75°~105°的随机值,接地阻抗为0~100 Ω,每10 Ω递增。共形成3 168个图数据样本,其中用于模型训练、验证和测试的样本比例为6 ∶2 ∶2。
3.2 噪声场景对故障线路定位的影响
为评估时-空多级去噪对噪声的抑制效果,选取希尔伯特黄变换(Hilbert-Huang transform,HHT)和Kalman滤波方法,作为对比方法进行分析。去除噪声数据后S-TGCN对故障线路的识别率R作为去噪效果的评价指标。
(15)
式中:TP为故障线路中识别正确的样本;FP为故障线路中识别错误的样本;FN为被误判为故障线路的其他线路样本;TN为其他线路识别正确的样本;C为全网线路总数。
对测试集数据添加不同的噪声水平,经不同方法去噪后输入到S-TGCN故障定位模型中所得到的故障定位结果,如表1所示。可以观察到,在不采取任何去噪措施时,当噪声水平到达20 dB信噪比时,故障定位模型的准确率仅为92.3%。可见,强噪声严重影响故障定位的精度。在三种去噪方法中,HHT具有显著的模态混叠现象,在强噪声的影响下,很难分辨出强噪声的变化。时-空多级去噪方法在去噪过程中考虑了相邻节点相似行波,当信噪比从40 dB增为20 dB过程中,识别率仅降低了1%,但Kalman滤波方法下降了4.4%。可见,时-空多级去噪方法对噪声有较强的抑制作用,能够适应复杂的环境干扰。

表1 不同噪声水平下去S-TGCN故障识别率
3.3 故障测距分析
为验证自适应多端融合故障测距方法的准确性。随机、分散地在输电网的多个不同位置F1~F6进行故障仿真。各故障位置及其定位结果如表2所示。可以看出,本文方法具有可靠的故障测距能力,识别结果均与实际故障情况相吻合。测距误差均小于100 m,表现出了较高的测距准确性和稳定性。
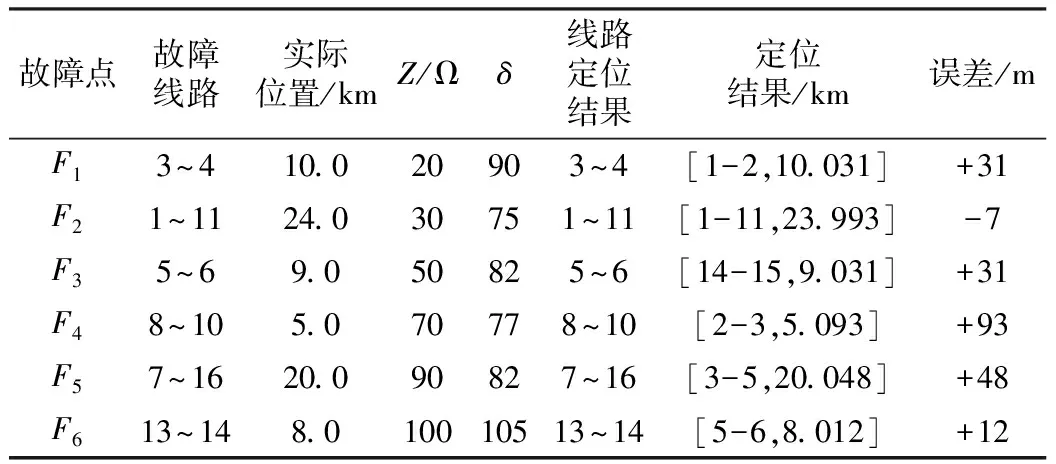
表2 不同故障点的故障定位试验结果
4 结束语
本文提出了一种基于时-空多级去噪和S-TGCN结合的输电网故障定位模型。利用时-空多级去噪方法有效地抑制了各测点的噪声数据,提高了故障线路定位精度。利用自适应多端融合故障测距方法,输电网的故障测距误差小于100 m。本文所提方法定位误差小,可降低巡线工作的人力物力,提高输电网运行的经济性。
