扑翼微型飞行器翼杆惯性载荷识别

孙世祥，徐塬皓，张雨浓，吴江浩，杜 锋*

（1. 北京航空航天大学交通科学与工程学院，北京 102206；2. 北京空天技术研究所，北京 100071）

1 引 言

扑翼微型飞行器的扑翼受载特征与飞行器的飞行特征密切相关，故而是领域内的研究热点。Zhao 等的研究表明扑翼后缘和扑翼柔性对其气动力的表现有显著影响，并建立了详细的气动力数据库［1］。Kang 等测试了弦向、展向和各向同性柔度对扑翼推力产生和推进效率的影响，并指出扑翼在共振频率附近拍打可以获得最大的推进力，而在固有频率的一半左右拍打可以获得最佳的推进效率［2］。Nicholas 等则提出了机翼突发俯仰运动的精确解，建立了包含柔度修正的推力和效率的表达式［3］。David 等通过实验证明了柔性翼膜的展向物性参数对推力的影响较大［4］。Arora 等建立了流固耦合条件下的扭转柔性模型［5］，该模型能够代表扑翼的真实运动和求解翼膜运动过程中的柔性变形。受流固耦合及非定常流动的影响，目前难以对扑翼受载进行准确建模或定量测试，这严重制约了飞行器的结构优化与气动效能的提升。例如Phan 等通过测量扑翼微型飞行器的功率，间接揭示扑翼的气动效能［6-7］。Coleman 等设计了300多种不同的柔性扑翼结构来筛选和优化扑翼气动性能［8］。这表明需要一种高效和准确测量扑翼受载的实验测量手段。

仿生扑翼由弹性翼杆和柔性翼膜构成，翼杆作为柔性扑翼的骨架结构，能够维持翼膜外形和承受载荷。在扑翼微型飞行器工作时，翼杆主要受到惯性载荷及气动载荷作用。翼杆在受载时，发生弯曲变形。因此可以通过翼杆的弹性变形特征来反演翼杆的受载行为。本文提出通过翼杆的变形来识别翼杆的受载特征的实验方案，研究裸翼杆在拍动过程中的惯性受载特征。

在翼杆的扑动过程中，其变形可以被非接触测量手段准确识别，如机器视觉测量。Krzysztof等通过高速摄像机识别悬臂梁的变形，比较视觉测量和加速度计的识别效率，验证其方法的精确性［9］。根据翼杆的变形来识别翼杆的受载特征是工程领域的力学反问题，考虑到实验测得的运动及变形参数必然含有噪音，此类反问题在多数情况下是不适定的，直接求解会显著放大噪音，导致噪音淹没真值，求解的结果没有参考意义。Fajardo-Fontiveros 等讨论了含有噪音的反问题，提出了理论上的噪音程度的上界限，一旦超过该界限，问题将不可解［10］。对此，一些学者采用将载荷重构为基函数向量和其系数向量的方法，将该反问题转化为求解或者拟合系数向量的优化问题［11-13］。其中，Ronasi 等采用正则化方法识别了列车车轮和铁轨接触时产生的周期性变化载荷［13］。同其他求解或拟合方法相比，正则化方法有诸多优势，如计算结果更加容易收敛，抗干扰能力更强，消耗的计算资源小。因此，使用正则化方法处理不适定问题具有独特优势。

以裸翼杆的拍动运动为载体，本文建立采用翼杆弹性变形特征来识别翼杆受载特征的实验方法，研究扑翼的翼杆在拍动过程中的惯性受载行为。首先采用机器视觉测量技术获取翼杆运动过程中的形貌特征，进而获取其弹性变形信息。其次建立了基于Tikhonov 正则化的翼杆载荷识别方法，基于悬臂梁模型，将未知载荷重构为幂级数的展开形式，转而计算其系数向量。通过广义交叉核实法确定正则化系数，最终通过翼杆挠度散点推演出翼杆上的载荷分布，得到了翼杆在一段时间内的载荷变化过程和角位移跟踪曲线。以此来研究翼杆运动过程中的惯性载荷演化行为，揭示其演化规律。

2 扑翼微型飞行器介绍

用于本文研究的扑翼微型飞行器主要由三部分组成，即动力系统、扑翼机构和控制系统。碳杆支撑扑翼外形，同时作为扑翼的骨架和前缘，起到了增加扑翼局部刚度和承受载荷的作用。图1所表示的是扑翼飞行器的总体布局。图1（a）为不带翼的模型图，所有部件均安装在机身固定座上。飞行器采用定制的空心杯电机驱动，由两节3.7 V的锂电池供电。空心杯电机工作电压在3.5～6.5 V 之间。当电机输入6.5 V 电压时，额定空载电流为0.08 A，额定空载转速约为54000 rpm，带翼扑动频率约为22 Hz，能够产生46～50 g 的升力。图1（b）为扑翼飞行器的真实布局，总质量约35 g，最大翼展为22 cm，高度为15 cm。翼杆的材质为碳纤维，直径为1 mm，其设计扑动角度为130°。在实际运行过程中，由于零件装配间隙和构件弹性变形的存在，翼杆的实际扑动角度约为170°。针对此，课题组前期的研究揭示了机构弹性［14］、间隙［15］和翼杆弹性［16］对扑翼运动的影响。

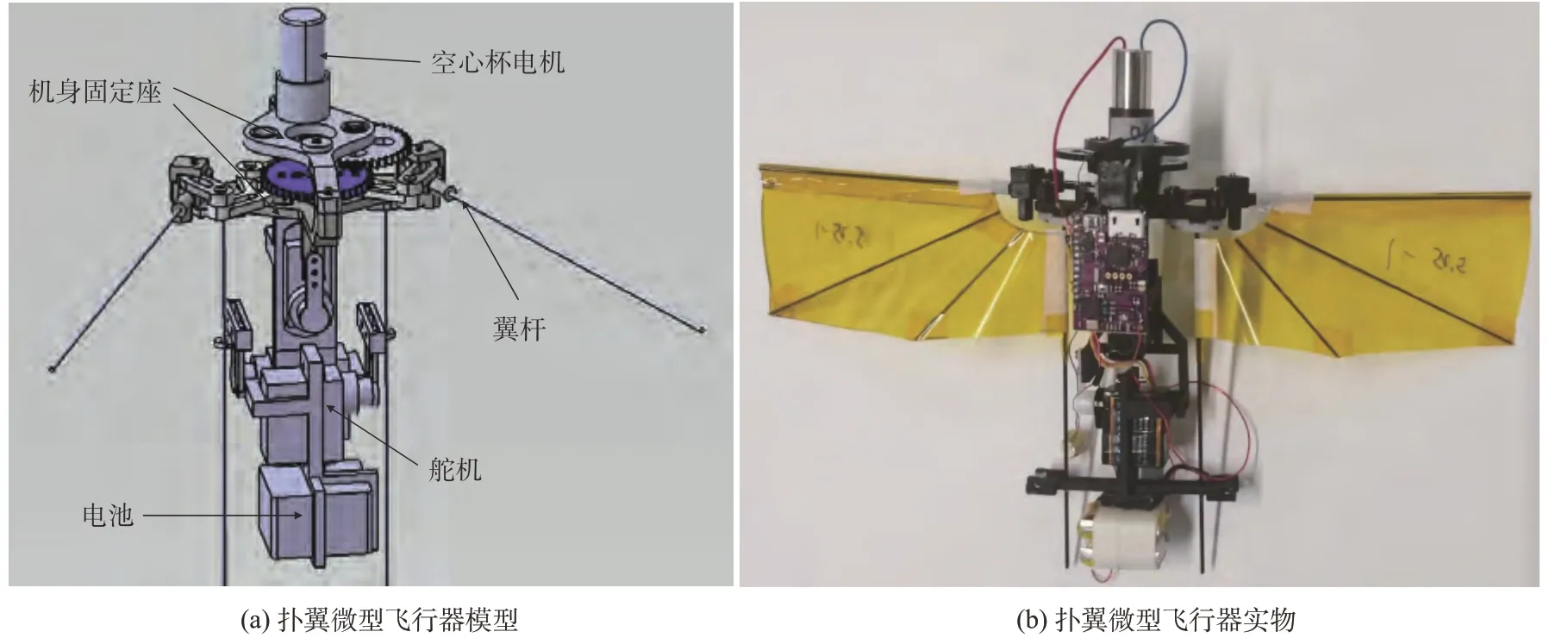
图1 扑翼微型飞行器的总体结构布局Fig.1 Overall structural layout of flapping-wing MAV

在扑翼飞行器实际运行过程中，翼杆作为扑翼的支撑结构，会时刻受到惯性载荷和气动载荷的作用，从而发生弯曲变形。因此，通过翼杆的变形特征，反演翼杆受到的载荷在理论上是可行的。本文将通过翼杆变形来识别翼杆载荷，建立基于翼杆变形特征的扑翼受载识别方法，用于扑翼飞行器在不带翼膜的情况下的翼杆惯性载荷识别。

3 翼杆轮廓和载荷识别方法

3.1 翼杆变形轮廓识别方法

3.1.1 提取翼杆轮廓

高速摄像机能够拍摄和记录扑翼微型飞行器翼杆的运动姿态，进而获得翼杆的变形轮廓，如图2 所示。翼杆的运动视为始终处在垂直于其转动轴的平面内，并且忽略其他方向的小变形和运动，因此单机位摄像机即可满足需求。摄像机输出的是扑翼微型飞行器的灰度图像，需要对其进行二值化处理。局部自适应的二值化方法能够将图像进行分块，再使用像素邻域的局部灰度计算每个像素的阈值，解决了因图像目标与背景阈值的差异而导致的图像处理形态不完善或者与背景发生混淆的问题［17］。若亮度和背景纯净条件得到保证，就能得到高质量的扑翼机构俯视图。

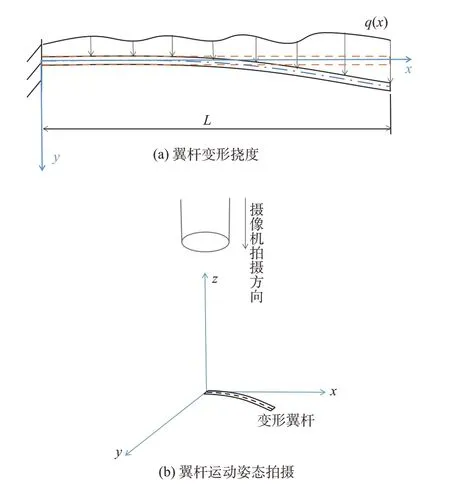
图2 通过相机拍摄获取的翼杆变形轮廓Fig.2 Deformation contour of wing rod obtained through camera photography

为了从整个扑翼机构的运动图像中提取出翼杆的运动姿态，本文使用帧间差分算法［18］，其基本原理为将相邻两帧或更多帧的图像进行差分运算，将不同帧的图像中对应的像素点灰度值相减，判断得到的灰度差是否超过设定的阈值，若超过该阈值，则可以判定为运动目标，静止的图像被消去。其算法为

式中，C(x，y，t1)是图像上任意像素点在t1时刻的灰度值，C(x，y，t2)是对应像素点在t2时刻的灰度值，H为阈值的设定值，Gp(x，y)为该像素点经过帧间差分算法后得到的图像值。经处理后就可以得到较为清晰的翼杆轮廓，过程如图3（a）～（c）所示，分别为灰度图像、二值化图像和经过帧间差分处理后的图像。

图3 提取翼杆轮廓的过程Fig.3 The process of extracting the contour of the wing rod

3.1.2 翼杆轮廓中心线识别算法

图像在进行帧间差分法处理后，仍会存在一些孤立色块以及缺陷，如图4（a）所示，因此要对图像进行优化和完善。在经过统计算法和开闭运算的处理后，就可以得到清晰的翼杆轮廓图像。从图4（b）中可以看出，翼杆轮廓图像描述的是翼杆在短时间内转动一定角度的过程，因而外形呈现扇形，干扰了翼杆变形轮廓识别。为此，本文采用了基于Steger 算法的中心线提取算法［19-20］，先通过施加二维高斯滤波将翼杆图像转化为类似正态分布线结构光的灰度分布，其效果如图4（c），再通过计算Hessian 矩阵的特征值和特征向量，实现对翼杆图像中心线的提取，并用中心线代表这段时间内的平均变形和平均位置，图4（d）中的实线代表识别得到的中心线。

图4 提取翼杆中心线的过程Fig.4 The process of extracting the centerline of the wing rod

最后，经过标定，即可将拍摄得到的中心线转化为翼杆变形轮廓的中心线坐标Sk。经过批量处理，则可得到一段时间内翼杆变形轮廓中心线的所有坐标值，作为载荷识别方法的输入量。有关图像处理过程的更多细节可参照张雨浓等的工作［21］。

3.2 翼杆载荷识别方法

翼杆转动时，可以简化为一个悬臂梁系统，如图2（a）所示。翼杆长度设为L，受到分布载荷q的作用，发生弯曲变形，符合小变形假设，均质且各截面大小相同。测量得到翼杆中心线的一组间隔均匀的挠度散点Sk(xk，yk)(k= 1，2，3，…，m)，在翼杆的几何形状和材料性能已知的情况下，通过挠度散点Sk识别其受到的分布载荷q(x)。但是由于Sk中含有噪音，该问题无法直接求解，因而使用基于Tikhonov 正则化方法［22］的优化框架解决该问题。

3.2.1 分布载荷q重构

直接求解分布载荷q较为困难，将其形式重构，写成幂级数的形式

式中，T1×(n+1)是n+1 维行向量，其中的每个元素t(j)=xj-1（j=1，2，…，n+1） 表示基函数项；R(n+1)×1=(r1，r2，…，rn+1)T为基函数对应的系数项，n是幂级数展开的阶数。此时，求解q的问题转化为求解系数向量R。只要得到一组R，就能够得到分布载荷q。

3.2.2 Tikhonov正则化方法

为求解分布载荷系数项R，引入基于Tikhonov正则化方法

式中，‖ * ‖表示求向量的2 范数。A(x)m×(n+1)为系数矩阵。Ym×1=(y1，y2，…，ym)T为m维列向量，在已知挠度Sk的情况下，可以完全确定A和Y。λ为Tikhonov正则化参数，已知系数矩阵A时，可以通过广义交叉核实法（GCV方法）计算得到。

翼杆的杨氏模量E和惯性矩I均视为常数。翼杆满足小变形条件，受到载荷发生变形时，其载荷和变形满足

式中，M为其上的力矩分布。为了得到M，使用微分方程求解

式中，F为悬臂梁上内力的分布。为了求解式（5）还需要确定其边界条件B(x)。对于悬臂梁系统，已知挠度y和转角y'在固定端为0，悬臂梁受到的力矩M和内力F在自由端为0。此时，边界条件可以用4个条件方程表示

式中，下角标表示选取的挠度散点，如y1表示第1个挠度散点的挠度值，Mm表示第m个挠度散点的力矩值。加入边界条件后，通过式（6）可以求解得到悬臂梁的挠度曲线y(x)。设有yk，经过微分方程组求解后，可以表示为

式中，向量W(xk)为基函数项T(xk)经过微分方程组运算后的形式。显然，对于一组挠度散点Sk(xk，yk)，可以通过求解式（5）～（7）得到系数矩阵A

3.2.3 确定正则化参数λ

引入Tikhonov 正则化方法后，增加了新的参数λ。有关选取参数λ的方法已有一套成熟的理论。本文选择应用广泛的广义交叉核实法［23］（GCV 方法）。GCV 方法给出了有关参数λ的验证函数

式中，I为元素均为1 的向量，trace 表示求矩阵的迹。当G(λ)取最小值时，取λ=λ0，其物理含义为寻找扰动误差和正则化误差之间的最优解。使用GCV 方法的最大优势是应用范围广泛，适用于绝大多数情况。

综上所述，通过翼杆的一组挠度散点Sk，可以通过基于Tikhonov 正则化方法的优化框架计算出其上的分布载荷的系数项R，进而求得分布载荷q。对高速摄像机拍摄得到的翼杆挠度图像进行批量处理，即可得到翼杆的载荷分布随时间演化的规律。

4 实验和结果

4.1 实验装置和实验台架布置

为保证有效采集翼杆运动时的变形轮廓，实验用扑翼机构去掉了扑翼飞行器的翼膜和控制硬件部分，只保留动力系统和翼杆部分。实验设置有专用夹具，并由3D 打印加工得到，可以保证机构中其他部分不会产生变形和位移，从而提高拍摄翼杆的精度。机构装配完成后的效果如图5 所示。由于翼杆空转时带负载较小，为了更好地模仿扑翼飞行器正常运作时的惯性载荷，输入电压设定为4 V，扑动频率约为20 Hz，与6.5 V 电压下，扑翼飞行器带翼扑动频率相接近。

图5 测试用扑翼机构Fig.5 Flapping-wing mechanism for testing

高速摄像测量平台用于拍摄记录翼杆的运动过程，该平台主要由高速摄像机、三脚架、扑翼机构支撑架、摄像机支撑架、补光灯、带夹具的扑翼机构、外界稳压电源以及计算机组成，此外还包括数据传输电缆、柔光布、背景白布等组件。高速摄像测量平台的布置如图6 所示，一台摄像机从扑翼的正上方竖直向下拍摄，可以观测到翼杆在拍动过程中的所有姿态。高速摄像机使用20 mm 的定焦镜头，光圈设置为4，拍摄帧率设置为4000 帧，分辨率为1024×1024 像素。本实验选用的高速摄像机为FASTCAM UX100 MINI，稳压电源使用UNI-T UTP1310直流稳压电源。

图6 高速摄像平台Fig.6 High-speed camera platform

测试用扑翼机构固定在支架上，通过两侧构件结合螺栓将其卡死，并结合底部的螺栓将扑翼机构固定在独立的光学实验板上，保证翼杆在正常运动的同时，方便拍摄。除此之外，扑翼机构支撑架和摄像机支撑架完全分离，避免调整扑翼机构支撑架时，触碰支撑架或高速摄像机，导致标定后的高速摄像机出现轻微位移，影响运动测量的精确度。高速摄像机支撑架采用高强度金属支撑架，可以很好地支撑和固定高速摄像机。背景白布、补光等组件能够保证视野的纯净度，将翼杆与背景进一步区分开，确保最终在图像处理阶段能够更好地获取翼杆图像。

4.2 实验参数选取

在翼杆载荷识别过程中，采用不同阶数的幂级数展开项，会对计算载荷结果的敛散性产生显著影响。对此，可以从低阶幂级数展开项开始测试，对于同一段扑翼飞行器的运动过程，计算每一阶的分布载荷。理论分析可知，幂级数的阶数过低，计算得到的载荷分布无法很好的跟踪真实载荷分布的变化；幂级数的阶数过高，计算结果容易发散。这两种情况都会造成载荷随着时间推移发生较大的突变，这显然不符合实际情况。比较不同阶数的幂级数计算得到的结果，选取载荷随时间变化连续性最好的结果，最后得到幂级数的展开阶数n= 3。

将翼杆根据其中心线的弧长方向，分为22份，即分为23 个挠度散点。因此，挠度散点数量m=23 。实验所使用的翼杆材质为碳纤维杆，看作均质杆。经过测量和计算，碳纤维杆的物性参数如表1所示。

表1 碳纤维杆的物性参数表Table 1 Physical parameters of carbon fiber rod

4.3 实验结果及分析

4.3.1 翼杆变形挠度

经过处理高速摄像机拍摄的视频，得到约0.5 s 内翼杆运动过程的高质量灰度图像，使用翼杆的轮廓识别方法，得到了每一帧翼杆变形轮廓和中心曲线。图7 展示了经过上述处理后得到的翼杆中心线挠度散点的分布情况：不同形状散点代表翼杆所处不同时刻的挠度信息，其中方形、圆形、三角形和菱形依次代表拍动时间增加0.5 ms的翼杆挠度散点。

图7 翼杆在不同时刻的挠度分布Fig.7 Deflection distribution of wing rod at different moments

为了探究翼杆挠度在时域上的变化，从前文所提及的23 个挠度散点中选择2 个观测点， 分别为自由端点和内部一点，记录其随时间的挠度变化。注意，这里的挠度变化是以翼杆未变形时的原始形状作为参考，即移除了翼杆转动带来坐标位置变化的影响。如图8（a）～（b）所示，分别表示自由端点和内部点的挠度随时间变化曲线。翼杆的挠度随时间分布具有很强的周期性，其频率约为20 Hz，符合机构本身的扑动频率，其最大挠度发生在自由端点，其值平均为0.015 m，且在一个周期内，大多数时间挠度值均在0.005 m 以下。Yang 等的研究表明，悬臂梁系统的挠度在相较于总长占比小于0.3 时，小变形假设带来的误差小于10%［24］。因此，此处使用小变形假设是合理的。挠度突变处代表翼杆撞击限位装置，远离撞击时刻的挠度小幅振动则源于翼杆上载荷的复杂性，主要包括由齿轮啮合带来的持续振动激励，由运动副带来的摩擦力矩，由翼杆限位装置带来的冲击载荷等。

图8 观测点挠度随时间变化曲线Fig.8 Observed point deflection over time

4.3.2 翼杆上分布载荷识别

图9（a）为根据某一时刻的挠度分布，使用载荷识别方法得到的GCV 曲线。通过GCV 曲线分布，取函数值最小时对应的λ值，即此时λ0=1.36 × 10-6。图9（b）为依据图7 中的挠度分布，识别得到的翼杆的载荷分布。载荷随着时间增加，逐渐由负值向正值转变，其物理含义为翼杆上载荷逐渐减小为0，直到反方向增加，这决定了图7中的挠度有同样的变化趋势。图9（c）中的曲线为根据图9（b）中各个时刻的识别载荷，通过悬臂梁的变形正向推导得到的翼杆变形挠度，散点则来自于图7。为定量比较识别挠度的精度，先计算出识别挠度相较于真实挠度的残差，再用翼杆长度L进行无量纲化，得到平均相对误差分别为3.6 × 10-5， 3.7 × 10-5， 1.4 × 10-5， 3.3 × 10-5，总平均相对误差为3 × 10-5。

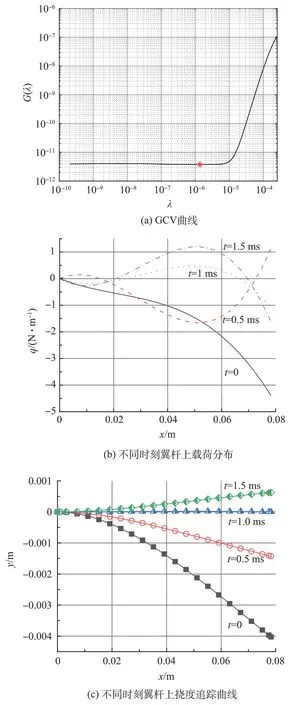
图9 识别载荷和识别挠度Fig.9 Identified load and identified deflection

4.3.3 翼杆在时域上的载荷分布

在经过翼杆挠度散点分布反演获得翼杆分布载荷后，对每一帧的图像进行批量处理，就可以得到分布载荷随着时间变化的规律。在观测点处识别得到的翼杆载荷随时间变化曲线如图10 所示。其中图10（a）表示自由端点受到的载荷，图10（b）表示内部点受到的载荷，其受到冲击力时刻的平均最大载荷分别约为30 N·m-1和17 N·m-1，在远离冲击载荷的时刻，其振动幅值较小，分别在±10 N·m-1内和±5 N·m-1内波动。可以看出，两个观测点处的挠度曲线和载荷曲线有着很强的关联性，翼杆受到的惯性载荷决定其变形。

图10 观测点载荷随时间变化曲线Fig.10 Observed point load over time

由于翼杆视为均质，线密度可视为常数，其上任意一点的垂直于翼杆的角加速度可以求出

式中，Lp为该点到转动中心的距离。再通过数值积分，最终得到观测点的角位移变化曲线，如图11 所示。图11（a）～（b）分别表示翼杆自由端点和内部点的识别角位移曲线。图中蓝色虚线代表通过翼杆载荷识别方法处理得到的曲线，而黄色实线是通过高速摄像机拍照记录的翼杆自由端的真实角位移。理论上，由四连杆机构输出的角位移曲线近似于三角函数，但是由于扑翼微型飞行器存在装配间隙和齿轮啮合现象，同时翼杆两侧转动角度最大位置处分别设有限位装置，导致翼杆运动时存在冲击和振动，使得其角位移曲线近似为三角波形。两个观测点处的跟踪曲线较好地贴合真实曲线，转动周期几乎完全吻合，局部最大误差容易出现在曲线的幅值点处，两个观测点处幅值点处的平均相对误差分别为17.6%和11.9%，总的幅值点平均相对误差为14.8%。

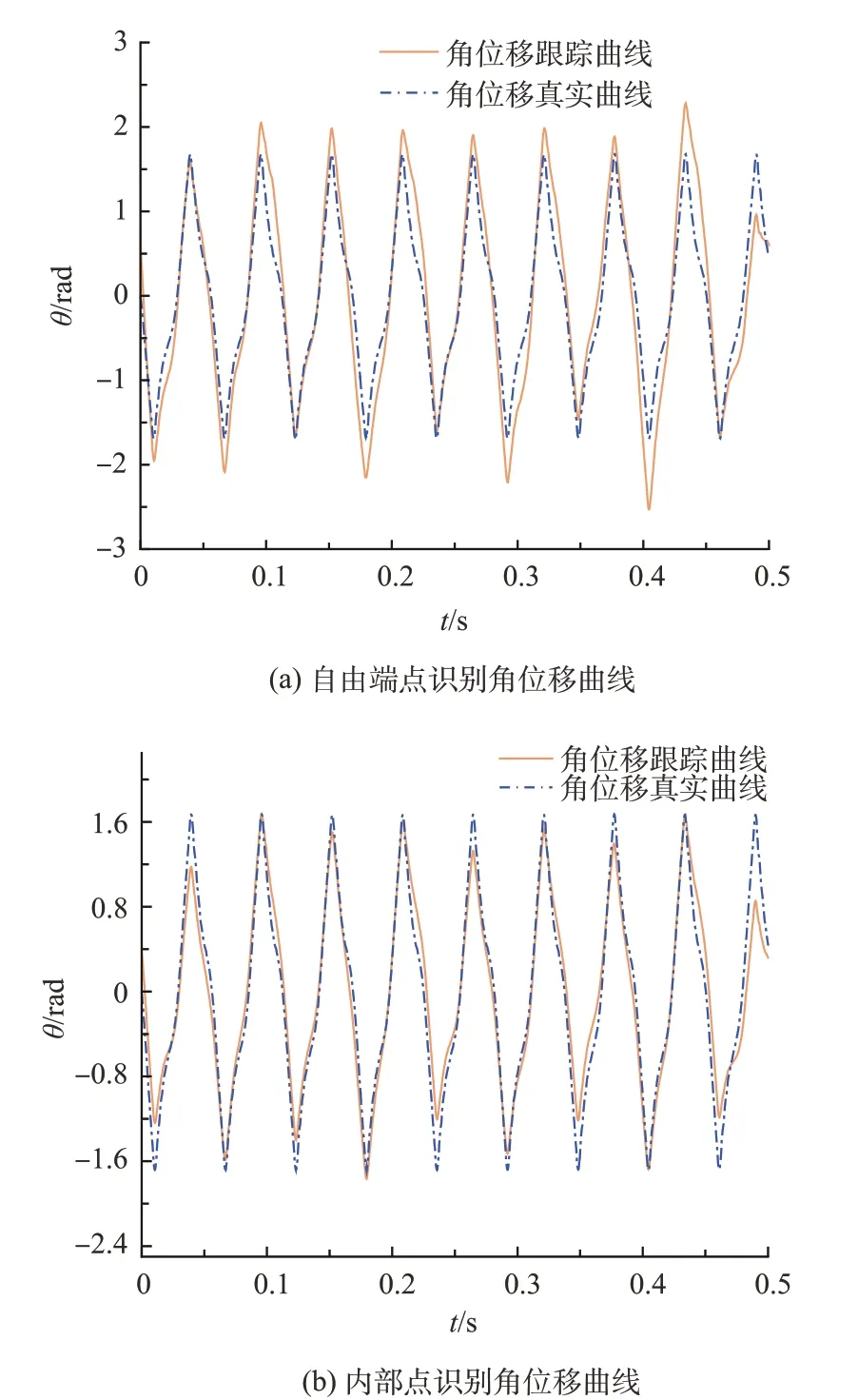
图11 识别角位移曲线Fig.11 Identified angular displacements

4.3.4 翼杆识别载荷在不同周期内的分布

扑翼飞行器工作时，其翼杆的周期运动可以分为四个阶段：从平衡位置到上极限位置、从上极限位置到平衡位置、从平衡位置到下极限位置和从下极限位置到平衡位置。实验中观测和记录翼杆每个周期内从上极限位置到平衡位置的过程，并标记翼杆转动中的三个位置，分别为：1上极限位置、2中间位置和3平衡位置，其示意图见图12。

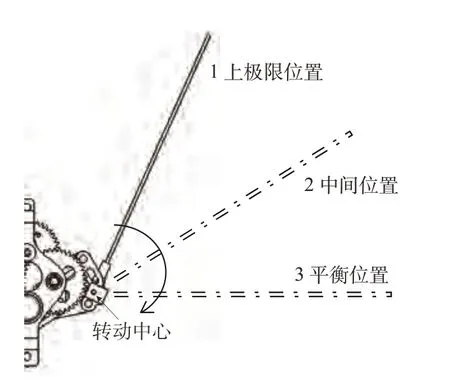
图12 翼杆运动至不同位置示意图Fig.12 Schematic diagram of the different positions of the wing rod

图13 中曲线表示在每个周期内，翼杆处于标记的三个位置时的载荷分布。其中，图13（a）表示翼杆处于位置1，此时翼杆所处时刻为撞击完成的瞬时，受到冲击载荷的影响，切向加速度处于最大值，翼杆上的载荷突变，其最大值集中在30～40 N·m-1之间。图13（b）表明翼杆处于位置2，此时翼杆所处时刻为向平衡位置的过渡时刻，切向加速度正在减小，撞击造成的影响仍然不容忽视， 载荷分布呈波形， 最大载荷集中在10～13 N·m-1之间。图13（c）则显示了翼杆处于位置3，即平衡位置时，此时切向加速度已经衰减至最小值，载荷整体较小，能够看出，从翼杆固定端到自由端，载荷逐渐增大，最大载荷集中在1.6～2.3 N·m-1之间。从图13 可以看出，在不同拍动周期内，基于翼杆挠度识别的载荷分布在三个位置处的一致性较好，这表明翼杆在每个周期内挠度分布和受载相似。

图13 翼杆上的分布载荷Fig.13 Distributed load on the wing rod

5 结 论

本文基于本课题组自行研发的扑翼微型飞行器，设计了基于翼杆弹性变形来识别翼杆惯性受载的实验方法。一方面，提出了运动翼杆的变形轮廓识别方法，包括采用二值化处理和帧间差分法提取翼杆轮廓，利用Steger算法和高斯滤波确定翼杆中心线，通过标定，最终得到翼杆变形挠度散点。另一方面，提出了基于Tikhonov 正则化方法的载荷识别方法，通过重构分布载荷为幂级数的方法，使用GCV 方法确定正则化参数，最终实现根据翼杆的挠度散点来识别翼杆上载荷分布的目的。

以扑翼飞行器不带翼膜的翼杆运动为对象，通过翼杆轮廓识别方法和翼杆挠度识别方法求得了0.5 s 内翼杆上分布载荷随时间的变化过程，确定翼杆实际扑动频率约为20 Hz；通过识别载荷得到的识别挠度能够很好地跟踪真实挠度，其平均相对误差为3 × 10-5；取得了翼杆上两个观测点的角位移识别曲线，其所有幅值点相较于真实角位移的平均相对误差为14.8%；分析了翼杆上不同周期的分布载荷，在不同周期的相同时刻，其分布载荷变化趋势相同，数值相接近。

在本文中，翼杆在运动时，同时受到扑翼机构系统内干扰和外部干扰，其载荷分布表现为多个要素叠加后的结果，主要包括由齿轮啮合带来的持续振动激励、由运动副带来的摩擦力矩、由翼杆限位装置带来的冲击载荷等，使得载荷识别得到的结果并非是理想周期驱动载荷的表现形式。为了识别带翼飞行器的真实气动载荷，有必要分别识别和确定不同载荷和激励的各自贡献。未来的研究将致力于实现翼杆上各种载荷和激励的解耦以及实现带翼飞行器翼杆的变形轮廓识别和载荷识别。