响堂铺2号大桥钢槽梁顶推施工导梁落梁方案分析
2023-10-12王晓磊刘畅张鹏刘焕举
王晓磊,刘畅,张鹏,刘焕举
(1.河北工程大学土木工程学院,邯郸 056107; 2.中国华冶科工集团有限公司,北京 100176)
当前桥梁的顶推施工中,往往通过钢导梁和临时支架等辅助性结构改善主梁在顶推过程中的受力情况[1-2],而导梁落梁是顶推施工的一个重要环节,将直接影响到工程的施工安全与施工进度。导梁落梁方案的科学设计可有效降低主梁结构的最大弯矩值,减轻顶推施工对钢桥主体结构的不利影响,减少工程事故的发生。因此对步履式顶推施工中导梁落梁方面的研究十分必要。
长期以来桥梁顶推技术的研究备受关注,前人为此做了大量的相关研究。张涟英等[3]考虑了导梁的截面形状及连接方式,发现导梁变截面点与顶板束锚固点的位置对主梁最大负弯矩峰值影响较小,导-主梁连接束大小对峰值影响较大。张亚丽等[4]针对钢拱桥顶推复杂的施工环境,提出了一系列步履式顶推的保障措施,有效解决了大悬臂顶推受力复杂、变形大等问题。靳锐勇[5]采用了长导梁法高位顶推技术,并通过工程施工验证了顶推过程中导梁落梁各阶段的施工步骤与技术要求,可为今后工程提供借鉴。高波[6]以某跨线工程为例,通过对比施工方案的科学性,选择最优方案,从而使得桥梁施工的安全隐患大大降低。时晓晔等[7]通过有限元软件对导梁结构建立多个模型,对比分析后得出了最优的导梁加固方案,为今后导梁局部的设计提供了理论依据。姜早龙等[8]为了保障大桥的安全施工,利用有限元软件和现场监测等多种手段验证了设计方案的可行性,同时表明在结构计算值未达到标准时,可通过对构件的优化,来达到规范的相关要求。
然而,现阶段的钢桥顶推施工中,在非对称式布置的支架上进行导梁落梁时,仍具有很大的风险,并且相关研究多为空白[9-15],因此对这方面的研究具有重要的现实意义。现采用MIDAS/Civil有限元软件对响堂铺大桥步履式顶推施工建立有限元模型,通过对导梁在非对称式支架上落梁的两种施工方案进行分析计算,确定最优的导梁落梁方案。
1 工程概况
响堂铺2号大桥为青兰高速公路40+62+40 m钢-混组合箱梁桥,主梁截面钢槽梁底宽为3.5 m,横断面为单箱单室,悬臂长度1 m,桥面板宽16.5 m。钢槽梁跨越青兰高速公路。桥梁设计基准期为100年,设计安全级等级为一级,适用环境类别为Ⅱ类,全桥采用整联步履式顶推施工法,施工立面布置如图1所示。

图1 顶推立面布置图
顶推导梁纵向长35 m,由2片等高度工字形实腹板钢板主梁组成,两片主梁之间由钢管组成的横向联系和上、下平面联系,导梁与钢槽梁通过焊接方式连接。钢槽梁和导梁均为Q345钢材,钢梁顶推到位后,采用整体落梁的施工方案,顶推施工中临时支架布置情况见图2。
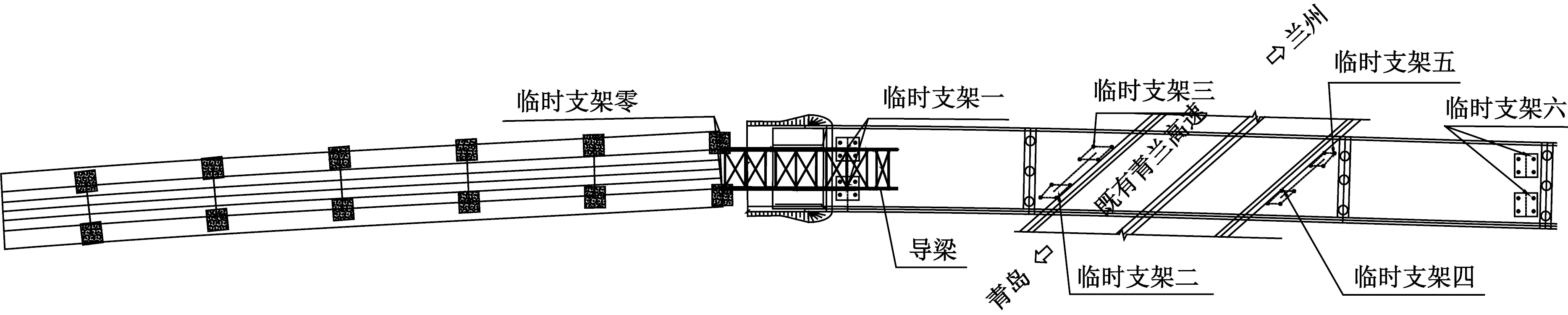
图2 临时支架平面布置图
当导梁从临时支架一顶推到临时支架四与五时,即导梁顶推至40~94 m并落梁的阶段,此时由于临时支架分布不均匀且顶推距离不断增加,若继续顶推,则会使导梁桁架破坏的风险增大,整体顶推系统可能会突发倾覆出现工程事故,阻断下方高速通行,给车辆和人员带来安全隐患,故此顶推阶段较为危险,选择出科学合理的落梁方案极有必要。在以往的顶推施工方案中,主梁往往采用一次性顶推到位,并整体落梁的方式,而在大跨度顶推施工中,则采用延长临时支架的纵向长度,减少导梁悬臂距离的方式[11]。针对响堂铺2号大桥的特殊情况,故依据经验并结合现场情况,设计出的方案一与方案二。方案一为顶推时导梁于40、45、49、86、90、94 m处每前进一次便进行一次落梁。方案二为顶推时导梁大部分处于悬臂状况,仅在支架处进行落梁。通过采用数值模拟手段对提出的两种方案进行对比分析。
2 顶推数值模型建立
为进一步对两种方案的合理性进行对比分析,现采用有限元模拟软件MIDAS/Civil建立桥梁顶推施工的有限元模型。以钢桥此前进行的顶推施工时导梁悬臂28、35和39 m监测数据为依据,验证数值模型,从而保证数值模型的真实性与可靠性。
2.1 模型搭建
根据结构设计图纸,对导梁结构进行划分后,通过搭建两工字梁间的桁架结构,建立起导梁的有限元模型。依照钢槽梁的工艺设计图和现场梁段的长度和焊接次序,建立出主梁结构单元,最终将主梁与导梁进行刚性连接,从而得出顶推施工的有限元模型,如图3所示。
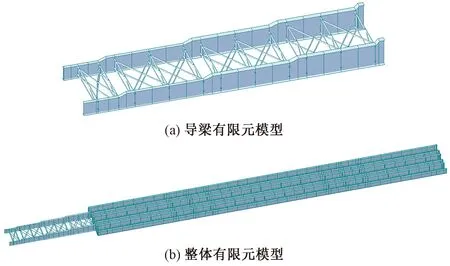
图3 顶推施工有限元模型
在模型边界条件的搭建方面,由于实际工程中,主梁是受自重作用而落在临时支架上的,两者并无焊接关系,故主梁结构与临时支架之间采用仅受压的弹性连接[16-17]。因为顶推施工中每次顶推距离有限,故有限元模型可以简化为前端悬臂的超静定连续梁,各步履式千斤顶可以认为与主梁之间为铰接,主梁后侧由钢架承台支撑部分的边界条件可认为是固定端[14]。
在模型分析方法的选取上,参考当前业界针对顶推施工中,利用数值模拟进行分析计算的两种类型:“倒退算法”和“前进算法”[6,15]。由于“倒退算法”中的节点不发生改变,因此更容易提取和记录主梁结构应力与挠度的数值,故本文中采取“倒退算法”对顶推施工的有限元模型进行分析和计算。
2.2 数值模型验证
通过调整边界条件,建立导梁悬臂距离分别为28、35和39 m的有限元模型,由有限元软件MIDAS/Civil分别计算出主梁结构的应力与挠度,并将其与实际监测值进行对比,如表1和表2所示。
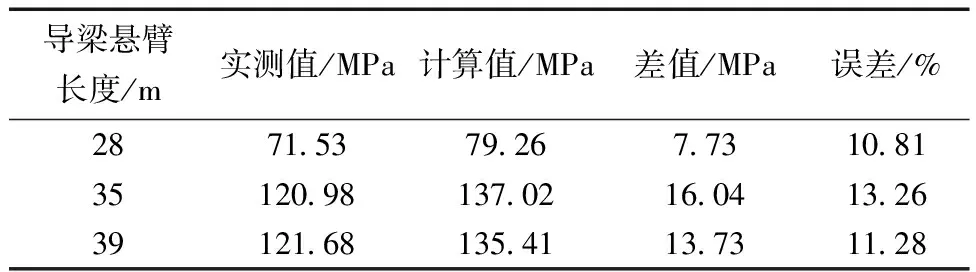
表1 顶推过程中导梁根部应力值
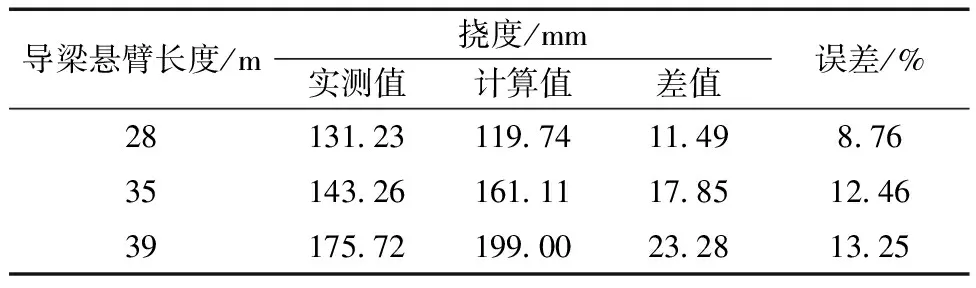
表2 顶推过程中导梁端部挠度值
由表1和表2可知:通过有限元模型分析出的结构应力及挠度值与实际监测数值基本吻合,应力值的误差分别为10.81%、13.26%、11.28%,挠度值的误差分别为8.76%、12.46%、13.25%。数据存在误差主要是两点原因:①焊接工艺的高温性和复杂性使主梁结构产生了无法消除的残余应力。②施工现场长期存在的风荷载。经查阅相关文献[14]发现误差值在15%以内,均属正常情况,而本模型计算的应力值与挠度值的误差均维持在13.5%以内,因而能够认定该有限元模型的计算结果应用于实际的桥梁顶推施工中是切实可行的。
在桥梁顶推过程中,主梁的受力随顶推的进行不断发生改变,为防止钢槽梁倾覆,现通过此模型分别模拟两种施工方案,对比分析导梁与钢槽梁的稳定性,最终确定顶推的可行性方案。
3 导梁落梁方案对比
3.1 方案一导梁落梁分析
方案一为顶推时导梁于40、45、49、86、90、94 m处每前进一次便进行一次落梁,总共落梁六次,由于两组非对称式临时支架为平行排列,两组支架间的最大距离达到44 m,主梁结构在两次落梁中,结构内力变化存在不同,故应对前后两次主梁落梁进行区分。将40~49 m设定为第一阶段,86~94 m设定为第二阶段,每阶段均独立建模[18]。通过计算得出的主梁应力及挠度结果如图4所示。
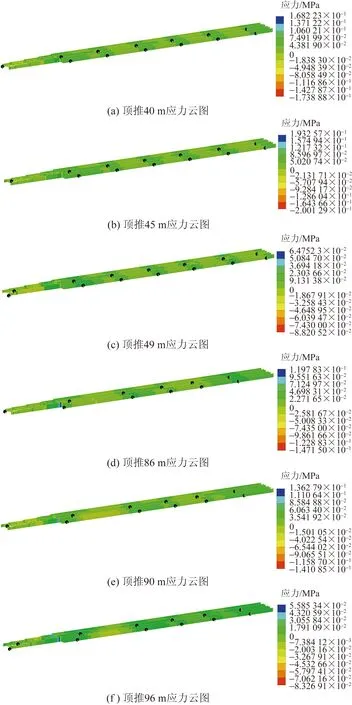
图4 方案一顶推40~94 m时的主梁应力
由图4可知,在方案一的第一阶段中,最大的应力为200.13 MPa,其出现在顶推至45 m并落梁时,并且应力最大值出现在导梁的多处桁架连接处,受拉与受压应力交替出现,其内部应力情况比较复杂,且导梁桁架的峰值应力比钢槽梁的峰值应力大约高116%,在实际的焊接工艺下,此种情况较为危险。而在方案一的第二阶段中,结构的峰值应力均控制在了150 MPa以内,最大应力也仅为147.15 MPa,并且最大应力为第二阶段的第一次落梁,往后的几次落梁中,应力值均呈下降的趋势。有限元模型在各工况下的计算结果见表3。

表3 方案一有限元方法计算结果
在方案一的第一阶段顶推施工过程中,钢槽梁主梁结构支撑位置发生改变,导致其截面的受力状态不断变化。导梁部分由于大部分处于悬臂状态且支撑点不对称,在重力影响下其应力数值较大且分布不均,相比主梁其他部分的结构应力,其数值高出20%~30%,同时导梁前端在落梁过程中总是有最大挠度值,随跨度增大而增大。而第二阶段与第一阶段恰恰相反,在第二阶段的非对称式落梁中,结构应力趋于稳定,无特殊应力出现。
3.2 方案二导梁落梁分析
方案二为导梁顶推过程中不予落梁,仅在第一阶段及第二阶段的顶推结束时,即49 m与94 m处进行落梁,悬臂长度分别为49 m和45 m,通过有限元模型对导梁悬臂的最不利情况进行模拟计算,从而分析出方案二钢槽梁的稳定性。图5为方案二中第一阶段的钢槽梁应力云图。

图5 方案二导梁悬臂为49 m时主梁应力及位移
通过计算可知方案二中钢槽梁的最大应力发生在导梁根部,数值为134.16 MPa,最大挠度为285.16 mm。而第二阶段的钢槽梁的最大应力发生导梁根部的桁架结构,最大拉应力为246.22 MPa,最大压应力为242.27 MPa,最大挠度为321.72 mm,结果如表4所示。

表4 方案二有限元方法计算结果
3.3 导梁落梁方案对比分析
通过总结上述两种落梁方案的计算结果,由表5可知方案一的第一阶段中,钢槽梁的结构应力过大,且分布复杂,可能会影响到施工的安全进行。而阶段二中,最大应力值却能均低于150 MPa,应力值反而较阶段一减少36%,此阶段比上一阶段更为安全。在方案二的第一阶段中,最大应力仅为134.15 MPa,与方案一相比结构应力最大值降低约33.50%且应力分布均匀[18]。导梁挠度虽为285.17 mm,但由于本工程采用步履式千斤顶等设备进行顶推施工,在整个顶推过程中可通过调整步履式顶推设备向上顶升来抵消钢槽梁及导梁向下的挠度,故方案二中所增加的导梁末端挠度值可通过顶推设备降低影响。然而由于主梁支座数骤降、跨度增加等原因,使得此方案第二阶段应力峰值骤增。相较之下,第二阶段中的方案二远不及方案一安全可靠。

表5 落梁方案计算结果对比
最终经两种结果对比分析,可知临时支架采用特殊布置方案时,导梁的落梁方案应采取不同的施工方法,当非对称的相邻支架为同侧最近时,采用一次性落梁的方案最佳,当相邻支架为同侧较远时,分布式落梁的方案最佳。因此响堂铺2号大桥的顶推落梁方案为:第一阶段选择方案二,第二阶段选择方案一。此种方案搭配,有效解决了非对称式支架布置的情况下导梁落梁的难题,减少了导梁落梁时的安全隐患。而且通过有限元模拟等手段,在积累经验与数据的同时,也节省了大量的时间成本,有效增加了桥梁施工的经济效应。图6为导梁悬臂时现场照片。

图6 方案二现场施工情况图
4 现场监测控制
施工监测是施工控制中尤为重要的技术手段[19],在顶推施工的工程中,常常对钢槽梁的结构应力及形变进行实时监测。在实际顶推过程中将钢槽梁与步履式顶推配套设备连接节点所在横截面设为关键截面,借助对钢槽梁应力进行实时监测的科学手段,判断其结构有无超过材料容许设计值,以达到保障钢槽梁施工安全的目的。根据有限元软件计算结果,将钢槽梁的跨中、四分之一处以及导梁的根部、中部和端部设为关键截面,通过安装应力应变计对其进行现场监测[20],钢槽梁标准截面应变计布置如图7所示。
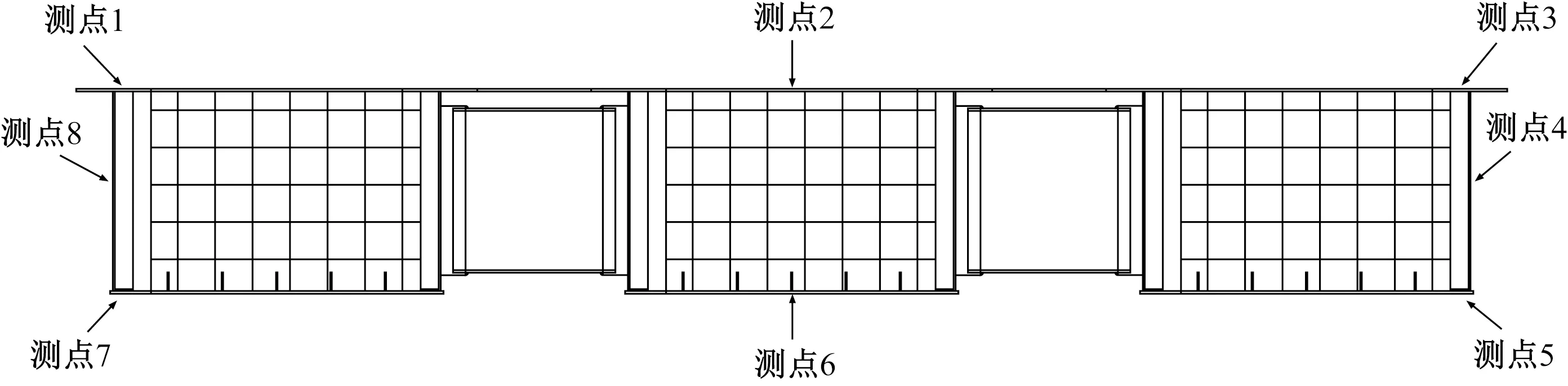
图7 钢槽梁标准截面应变计布置
表6给出了在实际顶推过程中各阶段的关键截面峰值应力实测值与计算值的对比结果。由分析可知:本文所建立的桥梁有限元模型得到的应力数值与现场实际监测值吻合情况良好,最大偏差仅为13.32%,且两者应力峰值所对应的截面均为导梁根部。
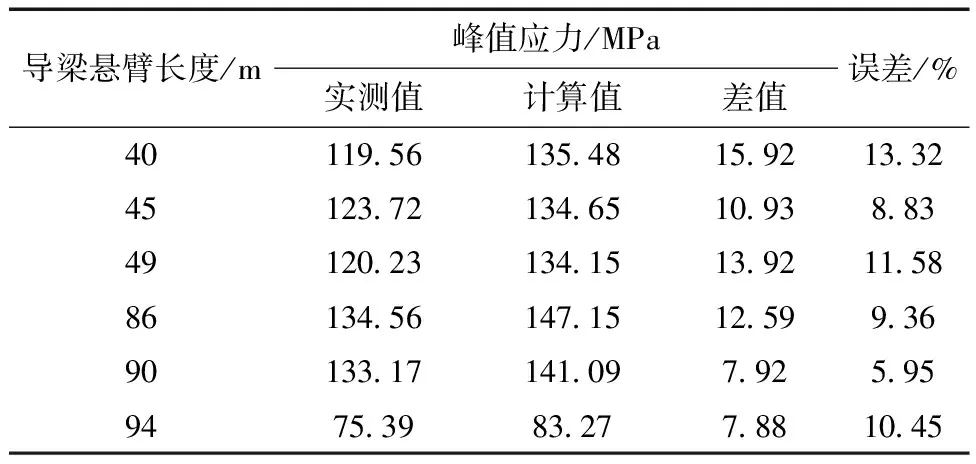
表6 顶推过程关键截面峰值应力
分析表6可知,在顶推施工中,顶推长度为86 m时实测值最大,为134.56 MPa,计算值为147.15 MPa,误差为9.36%。实测值跟计算值大致相同且实测值相对计算值较小,其误差产生的主要原因是:①焊接工艺的高温性和复杂性使主梁结构产生了无法消除的残余应力。②施工现场长期存在的风荷载。
在桥梁顶推施工过程中,钢槽梁自始至终处于运动状况,随着顶推的逐步进行其各截面的挠度也在逐渐发生相应变化,故而对导梁末端的挠度变化进行实时监测同样是保障临时支架和主梁安全施工的重要控制手段。表7给出了顶推施工过程中导梁前端到达临时支架并进行落梁时挠度的实际监测值与有限元模型计算值的数值大小与比较。

表7 顶推过程中主梁结构的最大下挠量
由表7能够看出,针对响堂铺大桥顶推施工所建立的有限元模型在计算导梁前端最大挠度方面具有极为良好的精准性,所得计算值与监测值的误差均不超过15%。由此可见本模型所得导梁前端挠度数据对实际工程施工是具有一定科学指导意义的。同时本模型用于判断导梁落梁方案是否可行,也是较为合理的。
5 结论
基于响堂铺2号大桥的特殊情况,通过分析两种方案下钢槽梁的受力特点,结合有限元模型对主梁应力值及下挠量的计算结果,在施工实测数据反复验证后,得出以下结论。
(1)针对响堂铺大桥的落梁施工,由两种方案分阶段组合而成的施工落梁方案更为合理,即第一阶段采用一次性落梁,第二阶段采用分步式落梁的落梁方案。
(2)在桥梁施工中,基于监测数据验证后的有限元模型,其误差能控制在15%以内。此种科学的建模方法,有利于得出结构真实的应力状态和挠度状态,能有效地对施工方案进行对比设计,提高工程效率,保障施工的安全平顺。
(3)通过现场监测与有限元模拟等手段的充分结合,最终使得导梁落梁方案达到最优,结构应力的实测值和理论值均可控制在150 MPa以内,此种分析方法可为今后类似工程提供参考。
(4)在非对称式支架落梁中,结构峰值应力一般多集中于导梁根部桁架处,顶推时应积极采取实时监测等应力控制措施。
