基于串并混联的机械手运动数学模型建立与数值仿真

汪再如

(安徽粮食工程职业学院 机电工程系,合肥 230011)

工业机械手无论是在工作效率还是控制精度,都远超过人工装配或半自动装配[1-4]。此外,机械手还可以在高危环境、极端环境及有毒有害环境下替代人工劳动,避免意外事故的发生[5]。从结构设计上来分析,机械手设计包括串联结构[6]、并联结构[7]和串并混联结构[8],其中串联式机械手设计具体包括直角坐标式、圆柱坐标式、关节式3种类型,串联机械手具有占地空间小、灵活度高、响应速度快等优点[9]。但串联机械手的整体刚度和承受能力有限,制造和采购成本也过高,限制了其应用范围。

并联机械手采用闭环式的结构设计,由上下运动平台和运动支链构成,使整个机械手结构具有了多个可操作的自由度[10]。按照自由度和机械结构的复杂程度,并联机械手可分为二自由度机械手、三自由度机械手,最高至六自由度机械手。除了结构结实耐用、购置成本低的优势之外,并联式机械手还具有刚度大、稳定性强、工作精度高等优点。鉴于串联机械手和并联机械手各自的优点,对将两者优点融合于一身的串并混联机械手研究,逐渐成为了机器人领域内的研究热点之一。本文从研究串并混联机械手的结构入手,以五自由度机械手结构为例,基于优化Denavit-Hartenberg(D-H)表示法在笛卡尔空间内构建机械手运动数学模型,并将机械手的运动过程进行了数值仿真,利用机构精度算法提升和改善混联机械手的控制精度。

1 结构设计与空间位姿变化

串并混联的机械手结构设计应满足工作空间和自由度的基本要求。首先,在机械手工作半径区域内避免存在障碍物,预留出3个轴向足够的半径空间;其次,依据具体的工况设定好机械手的工作节律;最后,根据机械手的用途和复杂程度设计机械手的自由度[11]。将等效串联结构中的承载部分替换成并联结构,以提高机械手整体的刚度和承载能力[4],替换后的机械手结构简图如图1所示。

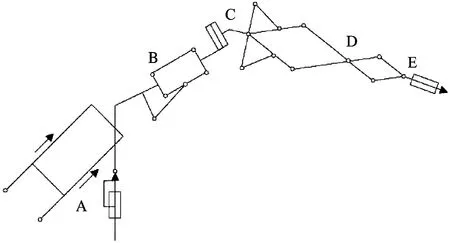
A—底座;B—机器人大臂;C—中臂;D—上臂;E—机械手终端。图1 五自由度机械手串并联结构简图

底座与U型件连接实现机械手与底座之间的二维转动,中臂匹配H型连杆分别与大臂及上臂连接,并实现360°自由旋转;上臂的伺服电机控制机械手伸缩和旋转[12],及机械手对标的物的抓取和摆放[13]。参数的输入与输出将决定终端机械手的空间位置关系,对于混联机械而言等效串联的部分需要进行下一步的位置正解,并联部分无须正解。基于D-H法构建五自由度机械手的等效串联关节空间坐标系,将核心参数设置为:Li为第i个机械手连杆的长度;βi为第i个机械手连杆之间的转角;γi为第i个机械手连杆的扭角;κi,i-1为第i个机械手连杆与相邻的第i-1个机械手连杆之间的偏置。

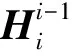
在正解求解过程中依据所列出的等效串联机械连杆参数,可依次计算出相邻连杆的空间位姿变化。从理论上讲,自由度越高,机械手的柔性越好,能做出更复杂的动作。但机械手的结构设计过于复杂、自由度越高,在求解反解时就越复杂,最终会导致混联机械手控制过程的难度过大,进而影响控制精度。

2 运动参数建模及动力学特性分析

构建串并混联机械手运动数学模型可以模拟出机械手运动过程中关节和连杆的运动过程,更有助于实现对末端执行器运动轨迹的精准控制[14]。在五自由度的机械手结构中,由于底座的运动对整体轨迹精度控制的影响较小,且终端关节运动的数值变化量较小[15],为了在运动数学模型构建过程中降低过程模拟与仿真的总体复杂度,在不影响总体动力学特征的前提下,仅讨论图1中机械手的B、C、D3个自由度的运动。以拉格朗日动力学方程为基础,将机械手运动过程中的驱动向量分解,即将其拆分成惯性矩阵A、离心力耦合矩阵φ和重力矩阵G的和,分解的过程为:

ξ=A(li)ai+φ(li,vi)vi+G(li)。

(1)

式中:ξ为广义坐标系下的驱动向量;li为广义坐标空间内第i个关节的位置变量;vi为第i个关节的运动速度;ai为第i个关节的运动加速度。机械手驱动向量受A、φ、G等3个因素及li、vi、ai的影响,这3个因素的具体影响过程分解为:

(2)

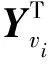
式中,χ为与机械手运动变化质量因素相关的定常向量。

机械手大臂采用并联结构,主要的功能是驱动串联的中臂、上臂,传递平台的动力。受到并联机构设计布局和动力学参数的影响,需要随时对机械手的运动方向做出调整。当机械手的丝杠螺母机构输入固定的运动矢量值时,动平台中心对应来自不同方向的运动输出,且分布在以坐标原点为中心的椭圆形轨迹上。由式(1)和式(2)可知,各个关键在运动中都会受到重力矩、离心力和耦合惯量的影响。当机械手处于静止状态时机械手的各关节转动惯量,如表1所示。

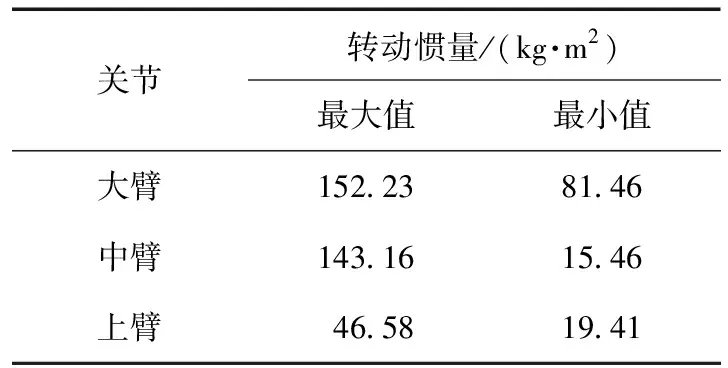
表1 机械手静止时各关节的转动惯量

在图1的串并混联机械结构中,大臂并联机构具有各向同性的特性,故本文的机械手性能分析主要围绕着大臂展开。通过空间位姿变化的分析,能够得到各关节角度与末端执行器之间的空间位姿关系,而机械手各关节的运动速度也会影响到机械手运动轨迹的偏离程度。针对于串并混联的机械手,本文模型具有较强的通用性,使用过程中依据D-H矩阵所构建的参数组合,可以计算出各关节的运动位置和旋转角度。雅克比矩阵求解是获取D-H参数值和空间运动位姿的关键步骤,通过空间位置方程推导出雅克比矩阵的解。在笛卡尔空间内机械手各个关节的线速度和角速度之间的关系,可以用雅克比矩阵描述(仍旧只考虑大臂、中臂、上臂3个关节)。

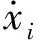
引入固定坐标系角速度的概念,并利用其分解坐标系旋转角速度,坐标系的分解过程如图2所示。

图2 坐标系旋转角速度的分解

机械手绕多个空间轴旋转,最终姿态控制为各关节旋转角速度的矢量和,在笛卡尔空间内机械手运动的最终角度ωend表示为:

式中:η2为大臂关节旋转的单位向量;η3为中臂关节旋转的单位向量;η4为上臂关节旋转的单位向量。

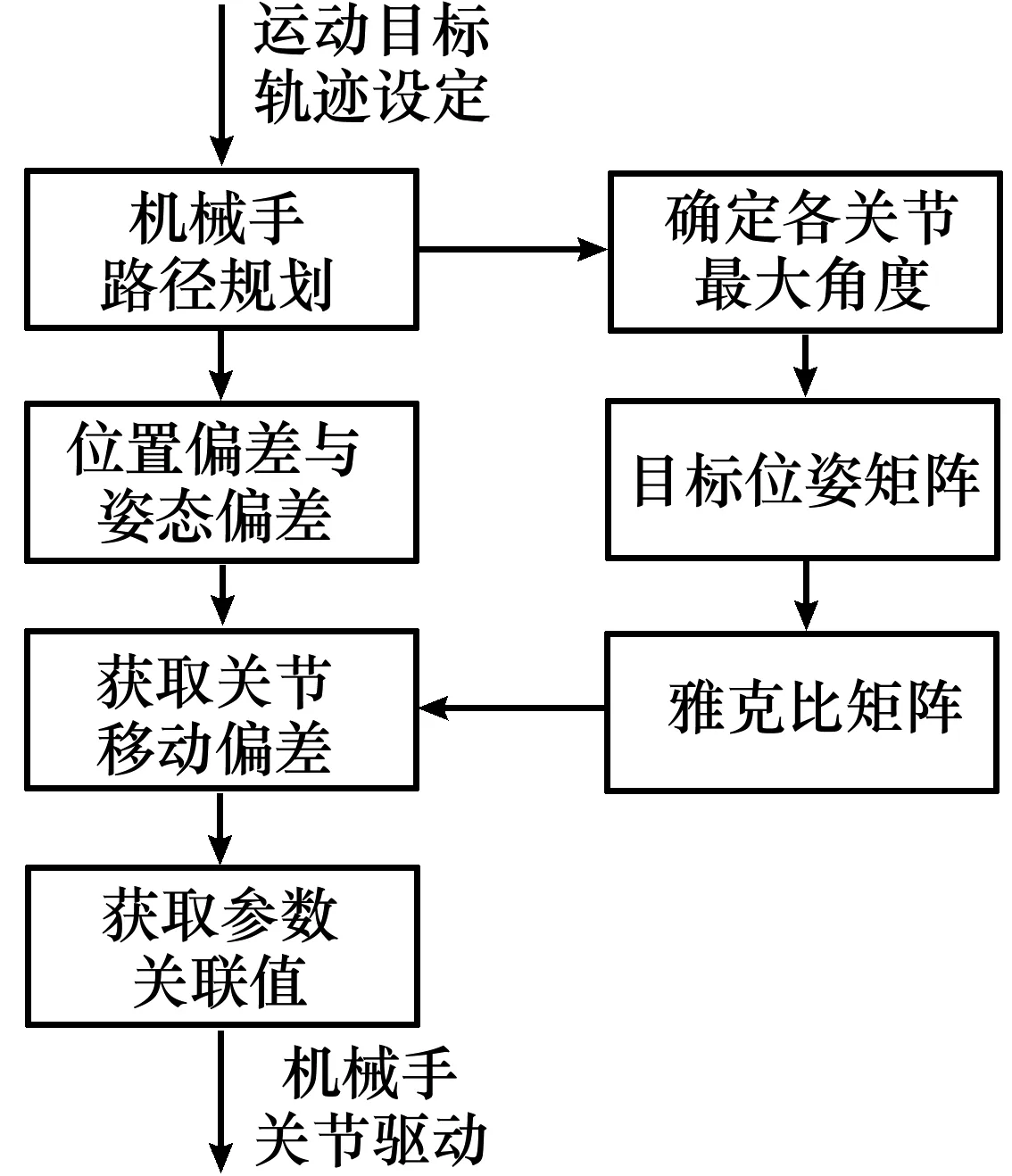
图3 串并混联机械手运动控制流程

3 数值模拟与仿真

3.1 系统调试

借助Matlab软件对本文模型做仿真测试,模型控制的仿真原理图如图4所示。

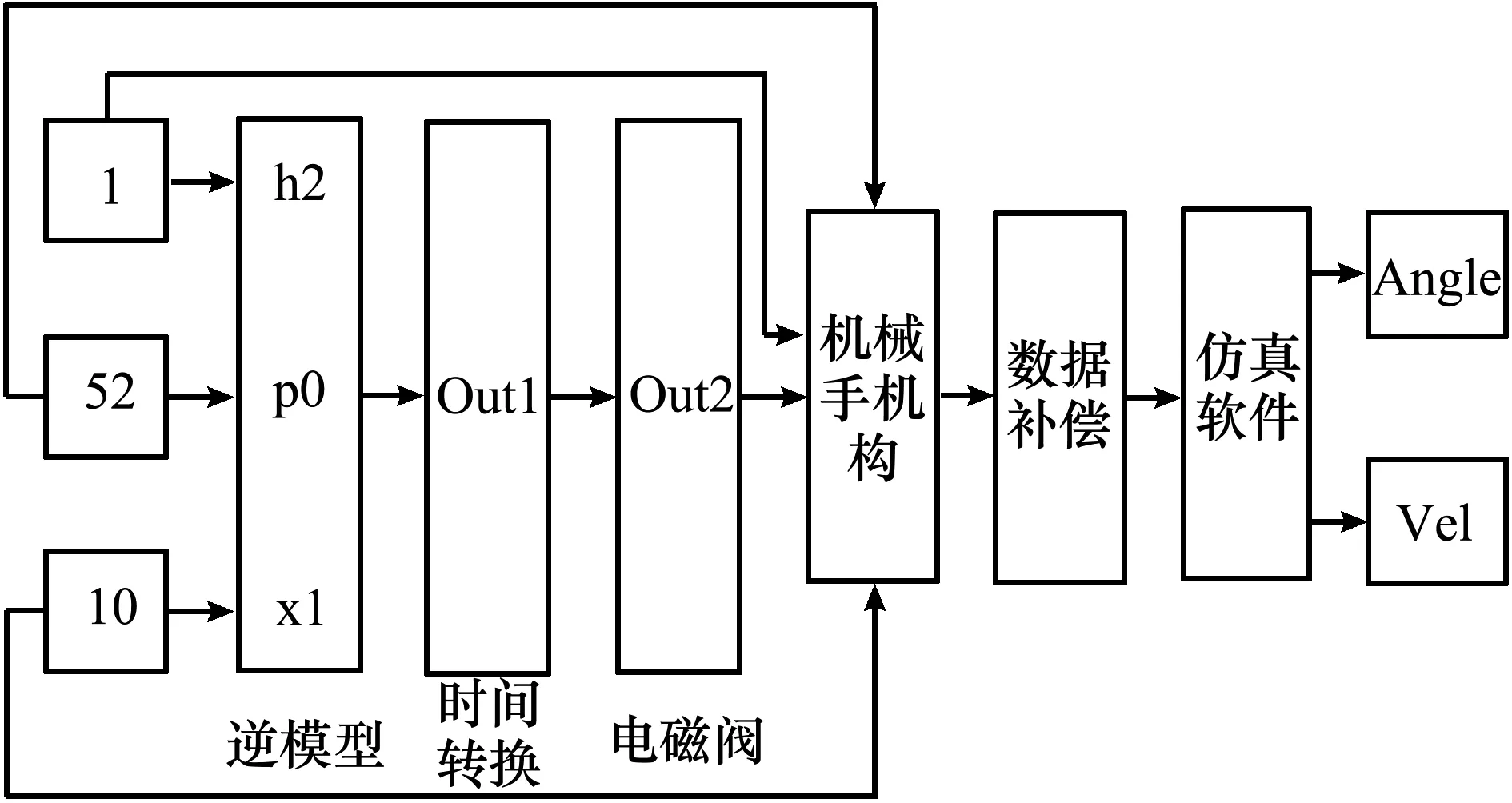
图4 串并混联机械手模型控制原理

将机械手传感器采集到的数值作为目标值输入模型,并与理论值进行比对,设定好串并混联机械手控制系统的初始状态。将逆模型控制系统的输出值调整为10 ms,并将通电脉冲的幅值调整为20 mm。如图5～7所示,在仿真环境下串并混联机械手运动模型的电压曲线、幅值曲线和转角曲线变化情况都在可控范围之内,未出现异常的波动,表明系统具有良好的稳定性。

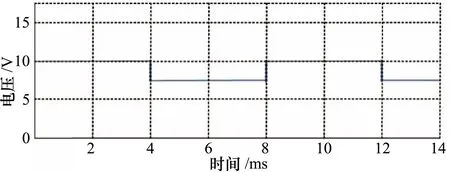
图5 控制电磁阀通电电压变化

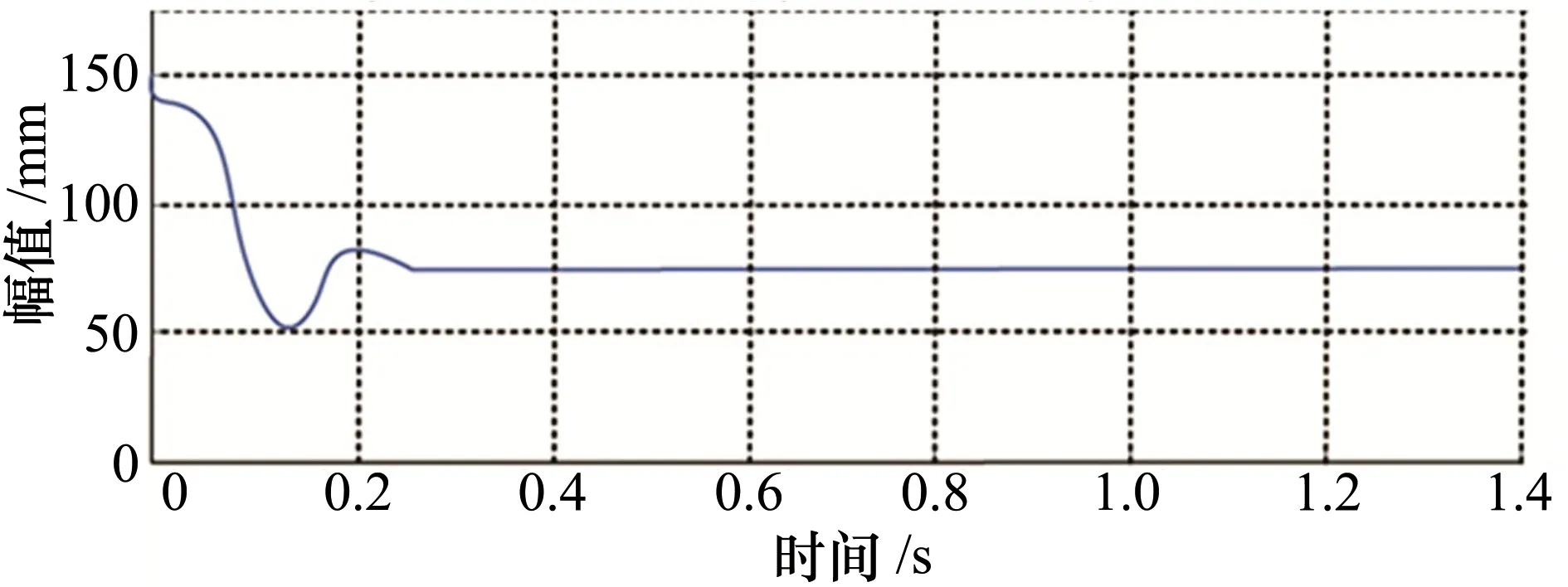
图6 幅值补偿曲线变化

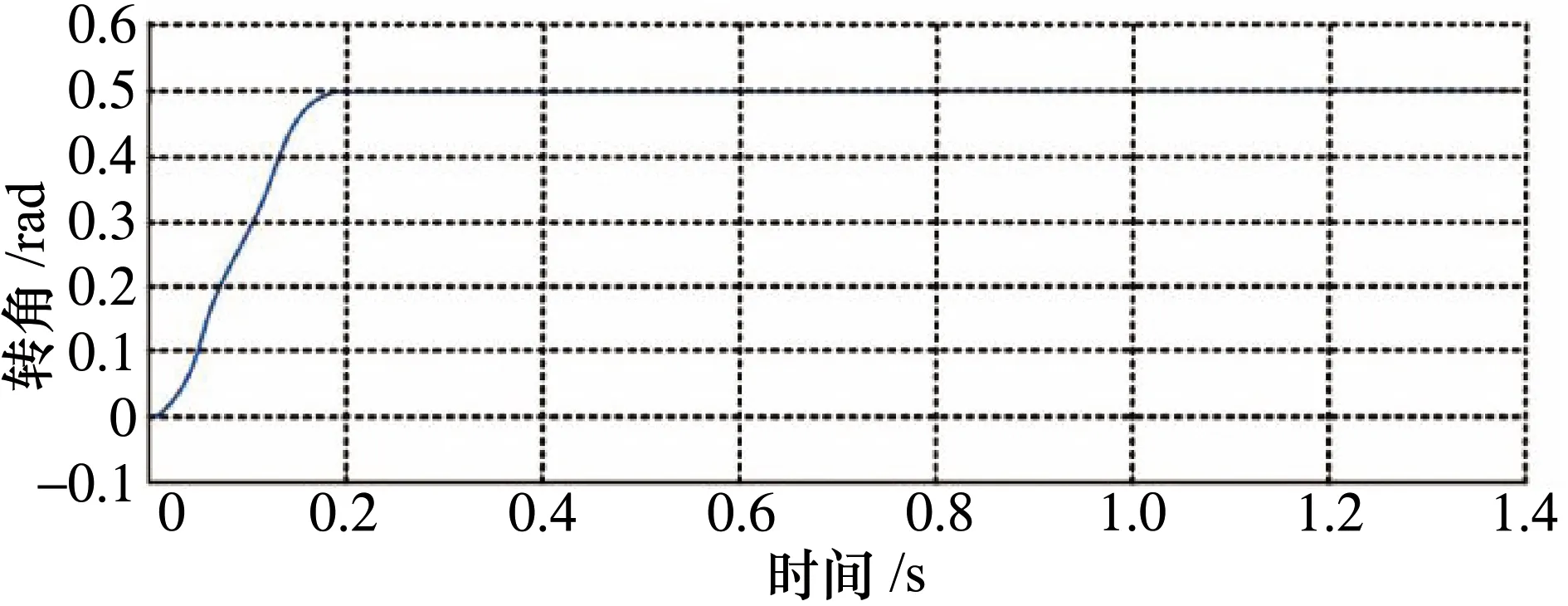
图7 运动转角曲线变化

3.2 数值仿真结果分析

在Matlab仿真环境下,验证串并混联机械手终端执行器在轨迹位移偏差控制、行进速度控制和加速度控制等方面的具体表现,同时引入传统串联控制方式参与对比,仿真结果如图8～10所示。

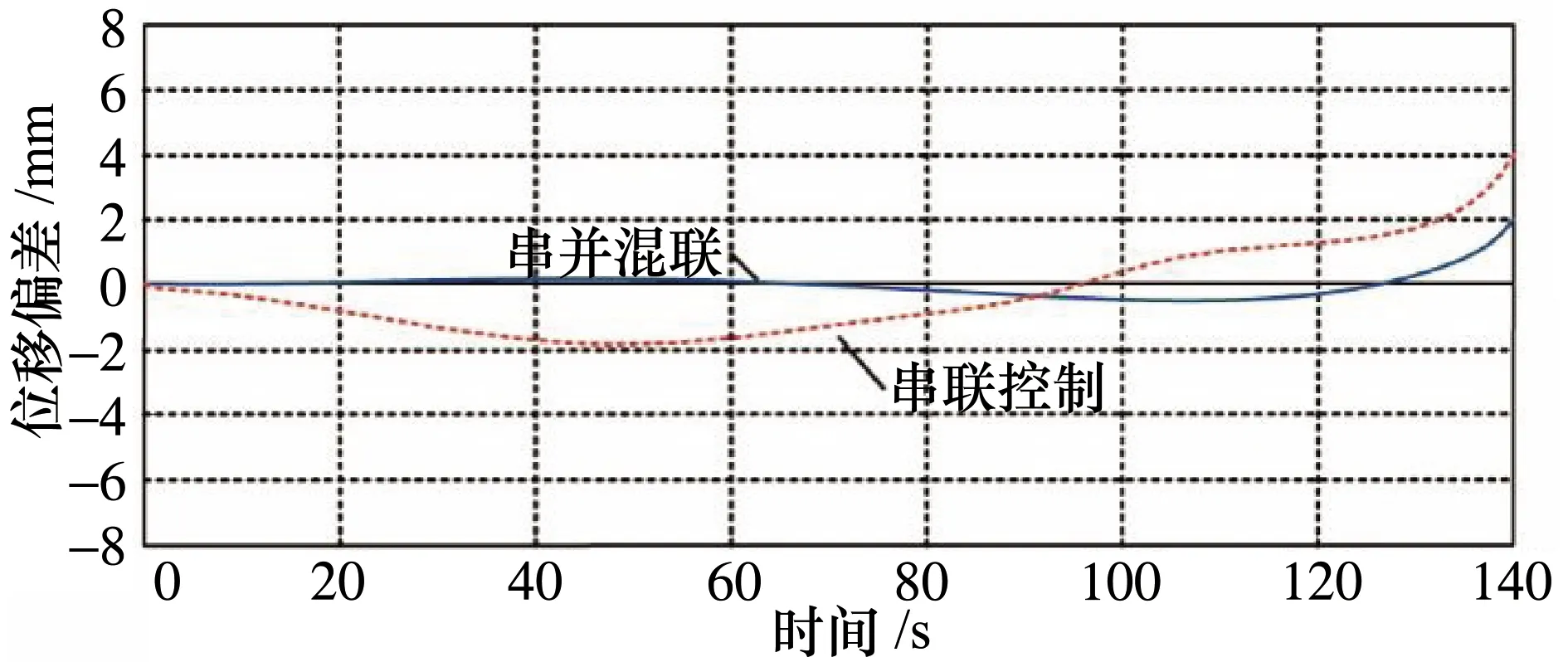
图8 终端位移偏差控制效果

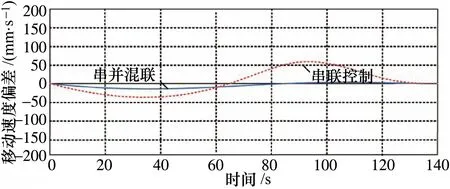
图9 终端速度偏差控制效果

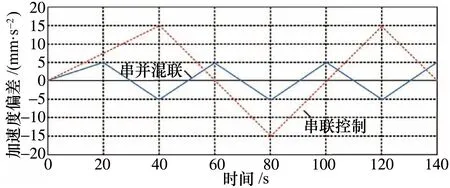
图10 终端加速度偏差控制效果

从位移偏差控制的角度来看,前120 s串并混联机械手的轨迹控制效果较好,轨迹规划趋近于理论值,120 s以后出现了控制偏差,需要通过后续的程序调整或算法补偿纠偏;而受到平台控制稳定性的影响,传统以单一串联方式控制,从20 s开始就出现了较大的控制偏差,仿真效果较差。从串并混联机械手速度控制和加速度控制稳定性来看,也要明显优于单一串联机械手的控制方式。尽管串联机械手在响应速度上更快,但由于稳定性较差,需要进行大量的算法补偿,控制成本过大,也无法获得更高控制精度。

在Matlab仿真环境下从机械手行进的理论轨迹中随机选定20个测试点,观测在整个过程控制中的轨迹偏离程度,如表2所示。

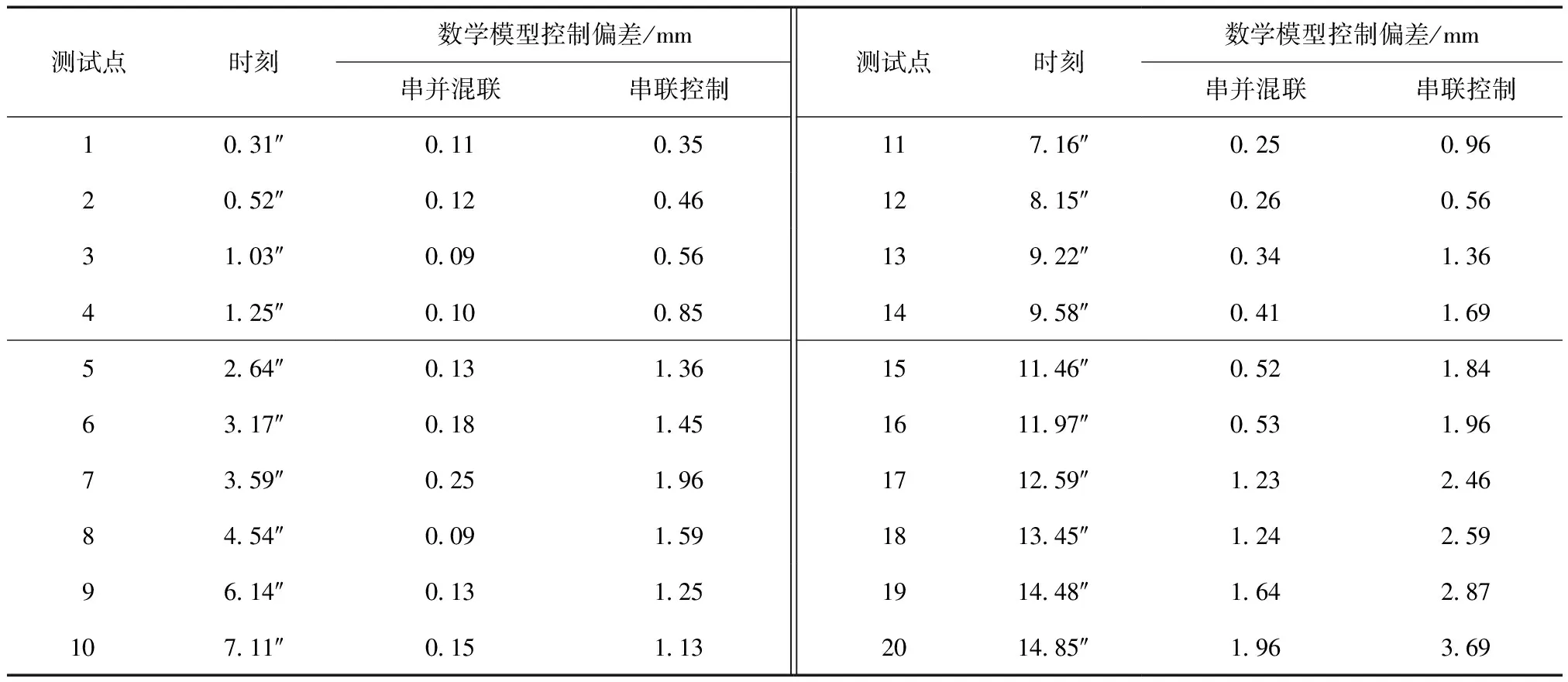
表2 控制过程中的轨迹偏差程度

从轨迹偏差的控制结果来看,所选取的20个测试点中,每个测试点串并混联机械手的控制偏差都要低于串联控制模式,这表明融合并联机械手的结构优势以后,机械臂的稳定性得到了提高。再仿真出串并联机械手5个关节在3个轴向的旋转角度偏差,仿真结果如表3所示。

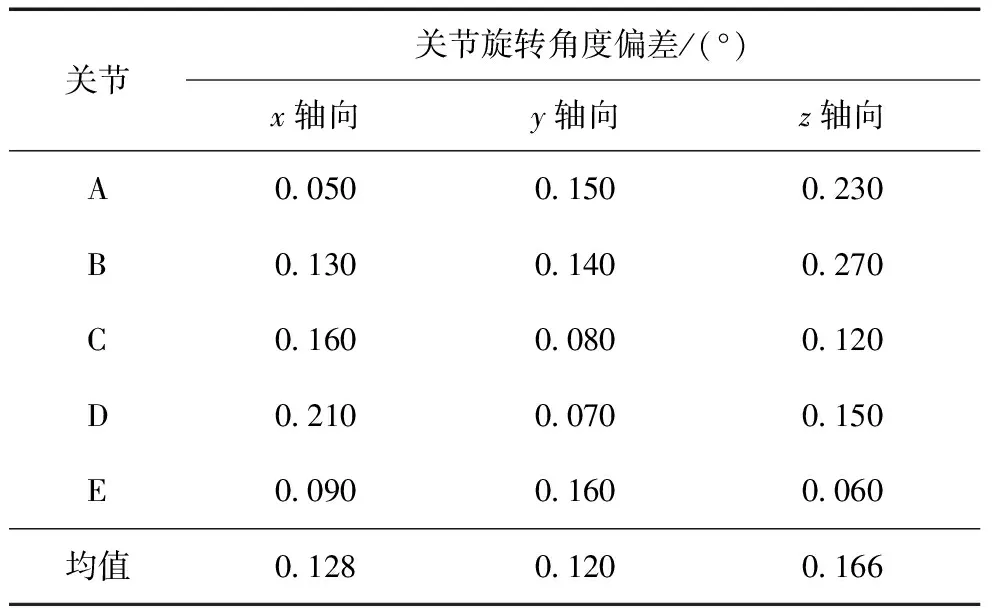
表3 串并联机械手各关节3个轴向的角度旋转偏差

仿真结果显示,串并混联控制模式下总体上5个关节在3个轴向的角度偏差均值分别为0.128,0.120,0.166°,关节旋转角度出现的偏差较小,趋近于理论上的运动轨迹。

4 结语

本文在仿真环境下构建了机械手运动数学模型,通过数值仿真的方式探究串并混联机械手的最佳控制方式。从仿真结果来看文中设计的仿真模型在电压控制、幅值补偿及旋转角度补偿等方面都具有一定合理性,在机械手的控制稳定性及控制精度上优于传统的串联控制方式。