流体惯性效应和裂隙几何属性对非达西系数的影响
2023-10-11汪慧香张昊明
汪慧香, 马 雷, 邢 坤, 张昊明
(合肥工业大学 资源与环境工程学院,安徽 合肥 230009)
裂隙介质中流体流动的非达西系数β的确定,对研究裂隙水污染运移、放射性废物地下储存和石油工程中的流体非达西流动具有重要意义[1-4]。对于流体在地质多孔介质中流动的β的影响因素和定量计算方法,相关研究成果较丰富[5-7]。文献[8]通过将介质和流体的性质与Forchheimer的系数联系起来,改进了用于描述多孔介质中非达西流动的Forchheimer方程,同时,首次将β作为湍流因子引入Forchheimer方程中。改进的Forchheimer方程为:
(1)
其中:P为压力;x为流动路径的长度;ρ为流体密度;g为流体重力加速度;J为总压降;Jv为黏滞力导致的压降;Ji为惯性力导致的压降;a1为黏性项系数;b1为惯性项系数;v为流体平均速度;μ为流体的动态黏度;k为介质的渗透率;β为流体流动时所受到的惯性阻力,也称为非达西系数或Forchheimer系数。
然而,文献[4,9]已经证明裂隙中的非达西流是由足够大的流体惯性效应引起的。参数β被广泛接受为“非达西系数”或“惯性阻力系数”,β作为直接决定Forchheimer方程中非线性系数大小的参数,对于量化和表征多孔介质中非达西流动具有重要意义。
基于实验室实验,文献[10-11]研究表明,多孔介质中的β仅取决于多孔介质的几何属性,与流体性质无关。文献[12]将多孔介质中β与渗透率之间的关系统一归纳为负幂律关系,即
(2)
其中:A为比例因子;b为无量纲幂指数(b>0);ko为仅取决于介质几何属性的固有渗透率。
相关研究结果表明,多孔介质中β的经验表达式通常与多孔介质的渗透率和孔隙度有关[13]。
近年来,含有ko和β的改进的Forchheimer方程被广泛应用于单裂隙的研究中[14-15]。为得到裂隙介质中β的量化模型,需要研究β与裂隙几何属性之间的关系。文献[16]研究得到围压条件下β与水力开度eh之间的负幂律关系;文献[6]研究单裂隙的几何属性对裂隙中非达西流动的影响,发现粗糙度对β有显著影响;文献[17]通过分析围压下不同裂隙的几何形状对β的影响,发现连通孔隙区域的不均匀分布对β会产生影响;文献[18]研究表明,eh仅取决于单裂隙的几何特性,且与流体惯性效应无关;文献[5]通过使用表观渗透率ka取代固有渗透率ko,将式(2)应用于单裂隙介质中。单裂隙的表观渗透率ka计算公式为:
(3)
eh=[12μQ/(Pw)]1/3
(4)
其中:Q为流量;w为裂隙宽度。
上述研究结果表明,单裂隙的几何属性(如粗糙度、开度等)决定β的大小,β与eh之间的数值关系也表明其与单裂隙几何属性的联系密切。然而,需要注意的是,无论是在多孔介质还是裂隙介质中,已有研究结果大多是在忽略流体惯性效应条件下的相关实验或数值模拟结果。由于流体惯性效应对β的影响几乎可以被忽略,β只表现出与裂隙几何属性密切相关的特性。一旦流体流动不再遵循达西定律,或者流体惯性效应不能被忽略,β是否仍然仅取决于介质的几何性质,目前尚不清楚。
理论上,含有β的Forchheimer方程的二次项系数代表流体因惯性力而产生的能量耗散,因此流体惯性效应与β可能密切相关。关于流体惯性效应对β的影响,相关研究中有一些间接证据。文献[2]通过用砂和玻璃珠填充的柱实验发现,β的变化可能与流体流态的转变相关;文献[19]认为β可能与流体性质有关;文献[20]通过数值模拟发现,单裂隙的ka会随着雷诺数的增加,即流体惯性效应的增加而降低;文献[21]进一步证明粗糙单裂隙的ka减小与足够大的流体惯性效应有关。由于ka与β之间的密切关系,流体惯性效应对ka的影响将进一步影响β。
本文通过揭示流体惯性效应对粗糙单裂隙中β的影响,提出在考虑流体惯性效应条件下β的量化模型。
1 数值模拟方法
1.1 二维单裂隙物理模型的建立
本文采用数值模拟的方法来探究流体惯性效应对单裂隙β的影响。虽然三维数值模拟在维度上更接近于真实裂隙,但是三维数值模拟方法需要大量的计算机资源和计算时间[22-23];相对于三维数值模拟,二维数值模拟虽然在维度上与真实裂隙维度有一定的差距,但大量研究表明,其结果也是可靠的[20],并且所需的计算机资源和计算时间也大大缩短,因此本文采用二维数值模拟方法。
在COMSOL Multiphysics软件中建立二维粗糙单裂隙的物理模型,物理模型参考文献[24]。为了实现单裂隙的不同几何属性,通过插入多边形粗糙元(梯形、矩形和三角形)、复制变换和布尔分割获得粗糙的裂隙上壁面,将下壁面设置为光滑壁。文献[24]研究表明,在类似具有规则粗糙元的单裂隙数值模拟中,粗糙元的密度D(即两个粗糙元之间的间隔与粗糙元的凸起度Δ之比)也会影响流体流动。为了消除D的影响,本文将具有不同凸起度(Δ分别为1.0、0.8、0.4 mm)的3种不同形状(矩形、梯形和三角形)的粗糙元密度设置为一个定值(D=6)。为获得足够的数据量,通过设置单裂隙的水力开度(eh)、粗糙元的形状和Δ,共获得45条具有不同几何属性的二维粗糙单裂隙。
为了量化单裂隙的几何属性,使用文献[5]提出的裂隙几何属性量化方法。二维粗糙单裂隙几何属性取值见表1所列。

表1 3种形状粗糙元二维粗糙单裂隙几何属性取值
表1中:em为机械开度;Rp为峰值粗糙度;RSD为相对粗糙度,用相对标准偏差(relative standard deviation)表示;Rrms为均方根粗糙度;bmax为最大开度。
1.2 裂隙流数值模拟
为符合裂隙流动的实际条件,选择层流模型作为整个数值模拟的模型框架,此模型将单裂隙中的流体设定为不可压缩牛顿流体,由流体连续性方程和Navier-Stokes方程共同控制,控制方程分别为:
ρ(u)u=μ2u-P
(5)
u=0
(6)
其中:u为速度向量,u=[uxuy];为微分算子。
数值模拟中使用的材料(水,默认为不可压缩的牛顿流体)需要在构建物理模型和选择流体模型后进行选择,这将直接决定流体的密度和黏度等物理参数。
物理模型的最左端设置为流体入口,最右端设置为流体出口。将物理模型的边界设置为不可渗透的边界,不发生滑动。入口和出口的边界条件设定为压力。入口压力定义为参数P-in,出口压力的大小定义为0,入口压力与出口压力之差即为压降(压降的大小直接决定着单裂隙中流体惯性效应的大小)。
COMSOL Multiphysics软件的计算流体力学模块是基于有限元方法对Navier-Stokes方程进行求解的,因此数值模型求解前需要对物理模型进行网格剖分。为保证数值模拟结果的准确性,本研究均采用极细化网格剖分方法。
1.3 非达西效应量化方法
流体惯性效应是β的重要影响因子,需要对其进行精确的量化。作为量化惯性效应的传统参数,雷诺数(Re)已被广泛用于多孔和裂隙介质的研究,其计算公式为:
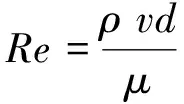
(7)
其中,d为裂隙的特征长度。
然而使用经典的雷诺数来量化单裂隙中的流体惯性效应存在以下问题:式(7)没有考虑可能导致强惯性效应的因素,如单裂隙的曲折程度和粗糙度;d的确定具有歧义,文献[25-26]使用单裂隙的机械开度作为特征长度来计算雷诺数,文献[4]使用水力开度。为解决特征长度的选择问题,文献[27]定义一种新类型的雷诺数,即Forchheimer数(Fo)来更准确地量化非达西效应大小,Fo计算公式为:
(8)
从式(8)可以看出,Fo为Forchheimer方程中惯性项和黏性项的比值,在计算时不需要确定特征长度。对Fo进行归一化处理,可得非达西效应因子E,即
(9)
E可反映流体在流动过程中惯性力耗散导致的压降占总压降的比例。
当Jv>Ji时,黏滞力引起的压降占主导地位,流动为弱惯性流,对应于0 作为Forchheimer方程惯性项系数的一个重要参数,β问题的探究必须基于非达西流。单裂隙中出现非达西流动的原因有很多,如复杂的几何属性[4]、局部涡流的形成[21,28]和足够大的接触面[29],其中普遍公认的是当流体惯性效应或流速足够大时,非达西效应便会出现[9,13]。本文通过增加单裂隙入口和出口之间的压力梯度(P-in),来获得足够的流体惯性效应,以实现单裂隙中的非达西流这一基本流态条件。以5个具有矩形粗糙元且Δ=1.0 mm的单裂隙为例,数值模拟结果如图1所示。从图1可以看出,裂隙中的水流偏离达西定律,但可以用非线性的Forchheimer方程很好地描述。 图1 粗糙单裂隙中流体流动的流速-水力梯度曲线 流体惯性效应对单裂隙ka的影响如图2所示。从图2可以看出,ka也随着雷诺数的增加而降低[28]。图1、图2结果表明,粗糙单裂缝中的流体流动出现显著的非达西效应,即形成了非达西流。 图2 流体惯性效应对粗糙单裂隙渗透率的影响曲线 基于Forchheimer方程可以得到不同单裂隙中不同惯性效应(用E量化)下的β。单裂隙粗糙度和流体惯性效应对β的影响如图3所示。从图3可以看出,单裂隙的β与相对粗糙度RSD成正比,与E的大小成反比。 图3 单裂隙粗糙度和流体惯性效应对β的影响 传统上,根据β的大小来判断流体非达西效应的强度[13],然而,从图3可以看出,对于具有恒定相对粗糙度的单裂隙,β会随着流体惯性效应增加而减小。根据式(9),E的大小由式(1)中的黏性项系数a1和惯性项系数b1确定,然而,根据文献[30]中a1与b1之间的量化关系,变化的β也会引起a1的变化,因此直接使用β的大小来判断非达西效应的程度并不准确。 为了量化单裂隙中的β,将β与多孔介质中渗透率k之间的关系扩展到裂隙介质中[5,12],即将式(3)带入式(2)中,可得: (10) 其中,C为标度参数。 根据式(10),除eh外,β的大小由比例因子A和幂指数-2b决定。因此,研究流体惯性效应影响下β量化模型的关键,在于如何量化惯性效应对上述2个参数的影响。粗糙度作为单裂隙最重要的几何属性之一,其大小会直接影响流体流动中的非达西效应[31-33],这也表明流体惯性效应与裂隙粗糙度对β的影响是相互耦合的,下面分析这些复杂的耦合效应。流体惯性效应(用E量化)对幂指数-2b、比例因子A及参数m的影响如图4所示。图4中,m为取决于单裂隙几何属性的参数。 图4 流体惯性效应对幂指数-2b、比例因子A及参数m的影响 1) 幂指数(-2b)的量化分析。从图4a可以看出:在弱惯性流下,幂指数-2b随着E增加而增加;在强惯性流下,幂指数-2b没有规律性的变化趋势,此现象也表明,当流体的惯性力占主导地位时,流体的流动状态会变得更加复杂;在弱惯性流下,具有相同Δ、不同形状粗糙元的单裂隙,其幂指数增长率(斜率)相似,幂指数-2b与E之间正比例关系的斜率随着粗糙元Δ(或相对粗糙度)的增加而增加,这也验证了粗糙度和非达西效应之间的正相关性[34]。根据粗糙度和流体惯性效应对幂指数-2b的影响进行无量纲分析,得到单裂隙粗糙度Rrms和E耦合影响下的幂指数量化模型为: -2b=28.74Rrms(E-0.637) (11) A为确定β大小的因素之一,如果将A假定为常数,那么幂指数-2b增加将导致β增加,这标志着非达西效应和β之间的正相关关系。 由图4b可知,即使在同一个裂隙中,A也会随着非达西效应的不同程度而变化。因此,需要通过进一步确定A的变化趋势来解释2.1节中发现的β与流体惯性效应之间的负相关关系。 2) 比例因子A的量化分析。无论是强惯性流还是弱惯性流,图4b结果与文献[7,24-25]的数据类似,即都表明A会随着E的增大而减小。然而,在围压或剪切条件下,A会随着E增加而增加[5-6,35]。应力过程将对岩石裂隙的几何属性产生较大影响,如在围压或剪切过程中,裂隙开度将进一步闭合,导致裂隙渗透率、粗糙度的变化和水体与固体相互作用加强[16],这可能是导致A与E之间异常关系的原因。本文未向裂隙施加应力,因此得到A与E之间的负相关关系,并与未施加应力条件的文献[7,24-25]的数据相吻合。 由式(10)可知,幂指数-2b通过乘数12b影响A。由2.2.1节分析可知,在弱惯性流下,E增加会导致幂指数-2b的增加,而12b则会降低。这解释了图4b中的弱惯性流条件下,A随着E增加而减小。受幂指数控制的乘数12b的存在会导致在分析E对A影响的过程中产生歧义。为了避免上述现象,A可以分解为式(10)所示的12b与参数C的乘积形式,然后对参数C进行初步分析。但在去除E对幂指数(或乘数12b)的影响后,参数C随着E的增加没有明显规律。为了解释这一现象,对参数C做进一步的数值分析。 本文定义一个新的参数m,其仅取决于单裂隙的几何属性,不会受到惯性效应的影响;C=mEn可以表示C受到流体惯性效应和裂隙几何属性的耦合影响,其中n为E的无量纲阶数。从图4c可以看出:对于Δ=1.0 mm的裂隙,当n=1时,m在层流(弱惯性流)下保持稳定;对于Δ=0.8 mm的裂隙,n=0;对于Δ=0.4 mm的裂隙,n=-1;在强惯性流下,m呈下降趋势。这表明E与C之间存在多阶反比关系。 此外,m的大小将受到单裂隙几何属性的影响。从图4c还可以看出:m随着粗糙度增加而增加;具有更大Δ(或相对粗糙度)且形状相同的粗糙元会产生更大的m;具有相同Δ、不同形状粗糙元的裂隙,m也不同;三角形的m大于梯形和矩形的m,这证实m也由几何形状决定。进一步分析表明,m与Rrms之间存在线性关系,即 m=lRrms (12) 其中,l为与粗糙元形状相关的无量纲参数,l矩形=7.437,l梯形=12.361,l三角形=33.540。 最后,结合式(10)~式(12),得到β、E和m之间的量化模型为: r1=-14.37Rrms(E-0.637), r2=28.74Rrms(E-0.637) (13) 式(13)为β量化模型,该模型考虑了流体惯性效应和裂隙几何形状对β的耦合影响。 1) 本文为了表征和量化流体惯性效应对非达西系数β的影响,对具有规则形状粗糙元的粗糙单裂隙进行一系列数值模拟。数值模拟结果表明,流体惯性效应(用非达西效应因子E表征)对β的影响十分显著,β会随流体惯性效应的增大而减小,并随裂隙相对粗糙度的增大而增大。 2) 本文着重量化分析0 3) 基于无量纲分析得到一个同时考虑流体惯性效应和裂隙几何属性的β量化模型。2 数值模拟结果与分析
2.1 流体惯性效应对β的影响



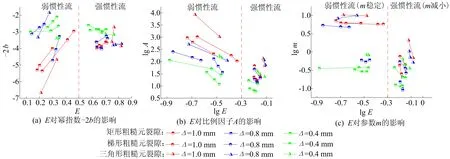
2.2 流体惯性效应影响下β的量化
3 结 论
