考虑水力耦合效应的超大直径穿江隧道开挖扰动分析

张红彬, 刘 武, 商兆涛, 过申磊, 张振华, 王佐才

(1.芜湖市轨道(隧道)交通工程质量安全监督站,安徽 芜湖 241000; 2.合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

岩体水力耦合作用研究在水工隧洞、水库岸坡、二氧化碳地质封存、深地资源或能源开采等诸多涉水工程的安全与性能评价中得到广泛关注[1-5]。对于大型过江隧道,其在修建过程中需要面对开挖隧道直径大、含水量高、自稳性差等重要问题,施工过程中对周边围岩扰动大,易出现地表变形和位移过大等情况,可能导致开挖面塌陷、江水突涌等安全事故[6-7]。因此,富水地层隧道修建不可避免地遇到与水有关的岩体水力耦合问题,受岩体结构及其所处工程地质环境的复杂与不确定性影响,水力耦合问题研究一直极具挑战。

针对隧道开挖扰动响应的模拟,相关研究大多主要考虑力学过程的影响[8-9],从水力耦合角度开展涉水隧道开挖扰动响应模拟的研究较少。文献[10]依据流固耦合理论,采用FLAC3D有限差分软件对厦门海底隧道开挖施工过程进行数值模拟,分析隧道开挖后的压力分布、洞周位移、塑性区、孔隙水压力分布等;文献[11]以长沙湘江大道浏阳河隧道为例,结合数值分析和现场监测数据,从流固耦合角度分析不同区段不同工况下的水下隧道开挖;文献[12]结合实际盾构施工监测资料,利用Plaxis软件模拟分析考虑与不考虑流固耦合作用下盾构机在砂卵石层中的掘进情况;文献[13]以某下穿库区铁路隧道工程为例,运用ABAQUS软件对比分析有、无渗流场作用和不同水深条件下,隧道结构应力变化规律以及围岩变形、塑性区和渗流场的变化特性;文献[14]利用FLAC3D有限差分软件模拟分析海底隧道不同地质条件下的耦合响应,发现水对海底隧道围岩的影响比断层大,在断层与地下水耦合情况下,可能出现隧道失稳。上述研究往往依托特定工程,研究成果受特定工程条件影响,且较少考虑岩体结构特征与渗透特性演化等的影响,相关研究有待深入。

本文以安徽省首条过江隧道——芜湖超大直径过江隧道穿越长江段为研究对象,基于TOUGHREACT软件岩体水力耦合细观力学模型[15],开展江底隧道开挖过程的水力耦合响应模拟,根据芜湖过江隧道工程特点,考虑长江水位变化、岩体水力耦合效应及泥水盾构支护水压对开挖隧道围岩变形的影响,并与不考虑水力耦合过程的一般模型结果进行对比,从细观力学角度揭示岩体结构特征、水力耦合效应等对不同江水位下开挖隧道周围围岩变形、江底地表变形、水压力分布规律等的影响。

1 工程概况

芜湖超大直径过江隧道为安徽省第一条在建的浅埋特长交通隧道,该隧道位于长江皖江段“大拐弯”处,西起芜湖市江北新城(鸠江区二坝镇)纬一路,东至江南主城的大工山路,距离下游的芜湖长江大桥约9.0 km,距离商合杭铁路芜湖长江公铁大桥约5.5 km。隧道全长约4.5 km,采用泥水平衡盾构掘进开挖,由江北工作井始发,向南掘进下穿长江后,到达江南工作井接收,依次穿过全断面土(砂)层、上软下硬地层、全断面岩层、破碎带、上软下硬地层、黏土层。盾构隧道为圆形断面,开挖直径为15.07 m,采用管片拼装式单层衬砌。江心部位隧道穿越地层主要为中风化粉砂岩,顶部距离江底小于14 m,而上部长江水深超过30 m,施工风险与难度大,在设计施工中需要重点考虑。在隧道开挖与江水渗流共同作用的水力耦合环境中,江底隧道围岩变形破坏与渗流规律受到岩体水力耦合效应的影响。本文分析水力耦合效应、岩体内部微裂纹结构特征与支护水压等对开挖响应的影响。

2 计算理论和条件

2.1 水力耦合分析基本理论

岩体变形破坏过程与渗流过程在本质上受控于内部微裂纹或孔隙结构特征[16]。水力耦合作用下,岩体内部微裂纹或孔隙结构发生变化,岩体产生损伤破坏,对变形和渗流过程产生影响。文献[15]提出的岩体水力耦合细观力学模型主要适用于水力耦合作用下,岩体变形破坏主要由内部钱币型微裂纹萌生、扩展与贯通所决定的情形。芜湖过江隧道穿江段围岩内部微裂隙发育,围岩变形破坏与内部微结构变化密切相关,本文采用该模型进行江底隧道开挖过程的数值模拟。文献[15]模型将材料宏观力学响应与细观结构演化联系起来,通过内部微裂纹滑移、损伤扩展和张开闭合等细观力学行为来模拟岩体宏观水力耦合响应。令岩体中含nc组任意分布微裂纹,采用细观力学方法,可得岩体力学本构方程与渗透特性演化方程如下:

Σ=

(1)

K=(1-φ)ksδ+

(2)

TOUGHREACT软件中水流运动控制方程为:

(3)

其中:ρ为水密度;q为单位体积质量源汇项;g为重力加速度;·表示张量的内积运算。

岩体细观结构变化由内变量d、β和γ的演化来表征,通过微裂纹局部法向应力Fβ、作用在裂隙面上的切向应力Fγ和损伤共轭热力学力Fd确定,即

微裂纹滑移剪胀引起内变量β和γ的演化采用关联的Mohr-Coulomb准则模拟,F=|Fγ|+Fβtanφc,φc为内摩擦角。微裂纹损伤演化准则采用可模拟全应力-应变过程的函数形式,即

(4)

其中:dc为损伤演化临界值;V0为微裂纹损伤扩展抵抗力最大值。

耦合模型的求解采用具有良好收敛性的双场交叉迭代算法,在每个时间步内,先基于式(3)利用TOUGHREACT软件进行水流运动过程模拟,确定计算区域水压力分布,然后基于预测-校正算法[16]对式(1)进行数值求解,根据内变量d、β、γ的值采用式(2)更新渗透系数,然后进行下一个时间步的计算,直至达到指定计算时长。

2.2 计算模型与条件

根据芜湖过江隧道穿越长江江心段的布置特点,建立有限元计算模型如图1所示,模型六面体网格数为5 406,节点数为11 120。模型平面尺寸为200 m×200 m,模型顶部为江底,其高程为-32.8 m,整个模型均处于长江水位以下,隧道顶部距江底13.57 m,围岩为饱和状态。计算模型顶部施加的荷载为水压力荷载,根据长江水位高程确定,江水位为4 m时,等效压力为0.368 MPa。计算模型底部和两侧均施加零位移法向约束。模型两侧设为隔水边界,顶部取为固定水压力边界,其值根据长江水位高程确定,初始时模型内部水压力呈梯形分布。

图1 过江隧道江心段有限元计算模型

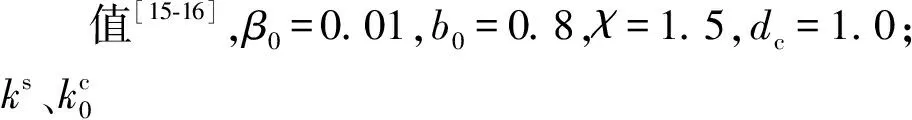
本文针对以下3种情形开展模拟分析:

情形1 根据长江水位变化规律,考虑长江水位分别为0、4、8、12 m的情况,分别采用耦合模型与一般模型进行江底隧道开挖模拟分析;分析过程不考虑支护水压作用,对应泥水平衡盾构掌子面发生漏水问题的情形,隧道开挖后洞周围岩孔隙水压力值降为0;岩体内部微结构假定呈各向同性分布;水力耦合计算时长为1 d。

情形2 长江水位取多年平均水位4 m,考虑岩体结构各向异性分布,采用耦合模型研究其对江底隧道开挖扰动影响,分析过程不考虑支护水压作用。

情形3长江水位取多年平均水位4 m,考虑泥水平衡盾构掌子面支护水压作用,水压力分别取0.40、0.50、0.58、0.65 MPa(后三者对应隧洞顶部、中心与底部水压力),采用耦合模型与一般模型研究支护水压对江底隧道开挖响应的影响。

3 结果与分析

3.1 开挖荷载作用下的隧道围岩变形分析

针对情形1,仅考虑开挖荷载作用时,基于一般模型分析得到不同江水位条件下江底开挖隧道围岩的水平和垂直位移分布如图2、图3所示。

图2 一般模型不同江水位下开挖隧道周围水平位移

图3 一般模型不同江水位下开挖隧道周围垂直位移

在隧道开挖卸荷作用下,洞周围岩呈现向隧道的变形趋势。由图2可知,开挖隧道周围水平位移最大值位于隧道两侧边墙处,且随着与洞周距离的增大而减小,沿隧道中轴线呈对称分布。

随着江水位增大,水平位移最大值由0 m江水位时的0.009 7 m逐渐增大到12 m江水位的0.011 9 m,增幅约23%。

由图3可知,最大沉降位于隧道顶部,0、4、8、12 m江水位下最大沉降值分别为0.014 2、0.015 6、0.016 9、0.018 2 m。仅考虑开挖荷载作用时,开挖隧道底部发生隆起变形,其值大于顶部沉降值,随着江水位由0 m增大到12 m,洞底隆起值由0.026 4 m增加到0.028 0 m,增幅约6%。

3.2 开挖和渗流荷载作用下的隧道变形分析

针对情形1,开挖和渗流共同作用下,基于耦合模型分析得到江水位在0～12 m之间变化时,江底开挖隧道围岩的水平位移分布如图4所示。由图4可知:考虑水力耦合过程影响时,在开挖隧道两侧边墙和江底地表均产生较大的水平位移。0、4 m江水位时,最大水平位移发生在隧道两侧边墙处,分别为0.010、0.011 m;随着江水位增大,渗流对岩体水平位移的影响增强,8、12 m江水位时,最大水平位移发生在江底地表,分别为0.012、0.013 m。

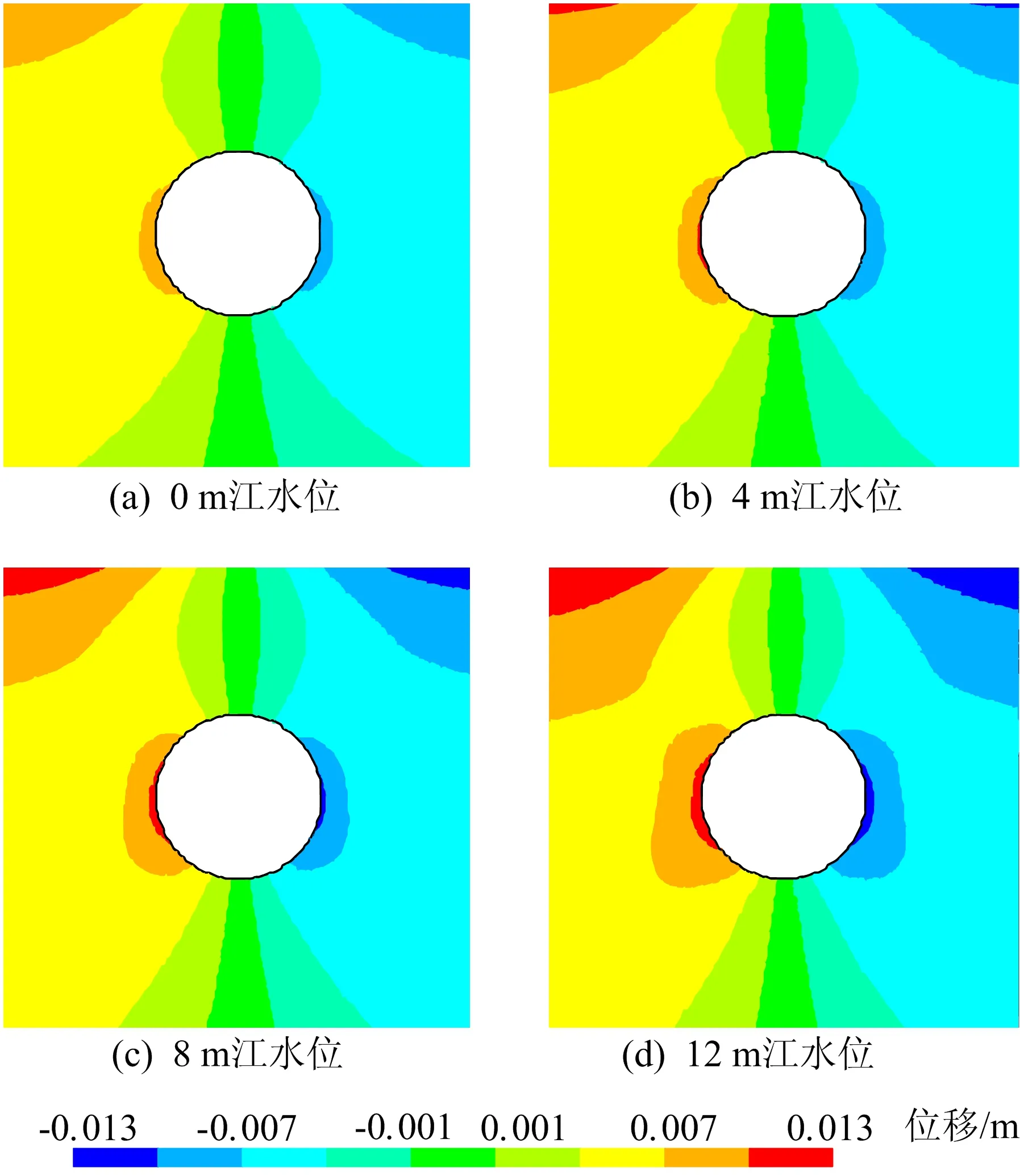
图4 耦合模型不同江水位下开挖隧道周围水平位移

隧道在开挖和渗流共同作用下,洞周岩体的垂直位移分布如图5所示。

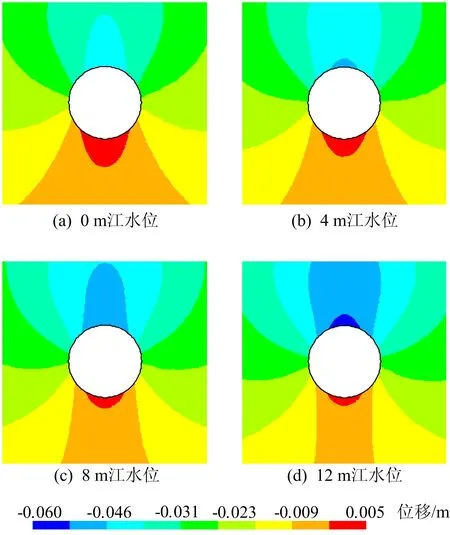
图5 耦合模型不同江水位下隧道开挖周围垂直位移

由图5可知:洞周岩体在开挖隧道顶部产生显著的沉降变形,而隧道底部的隆起变形却非常小;随着江水位增大,开挖隧道顶部沉降逐渐变大,而底部隆起值减小。在0、4、8、12 m江水位下,开挖隧道顶部沉降最大值分别为0.043 8、0.048 0、0.052 4、0.056 3 m,底部隆起最大值分别为0.004 7、0.003 7、0.002 5、0.001 8 m,开挖隧道底部隆起值比顶部沉降值小1个数量级。

渗流对开挖隧道围岩变形的影响与水压力分布密切相关。不同江水位下开挖隧道周围岩体内水压力分布如图6所示。由图6可知,开挖隧道周围存在明显的水压力降低区域,江水与洞周远区地下水向洞内渗流,从而引起围岩产生变形。

图6 耦合模型不同江水位下开挖隧道周围水压力

3.3 水力耦合效应对隧道开挖后江底变形影响

为了进一步评价水力耦合效应对地表变形的影响,针对情形1,采用一般模型与耦合模型分析不同工况下隧道开挖引起的江底竖直变形,结果如图7所示。

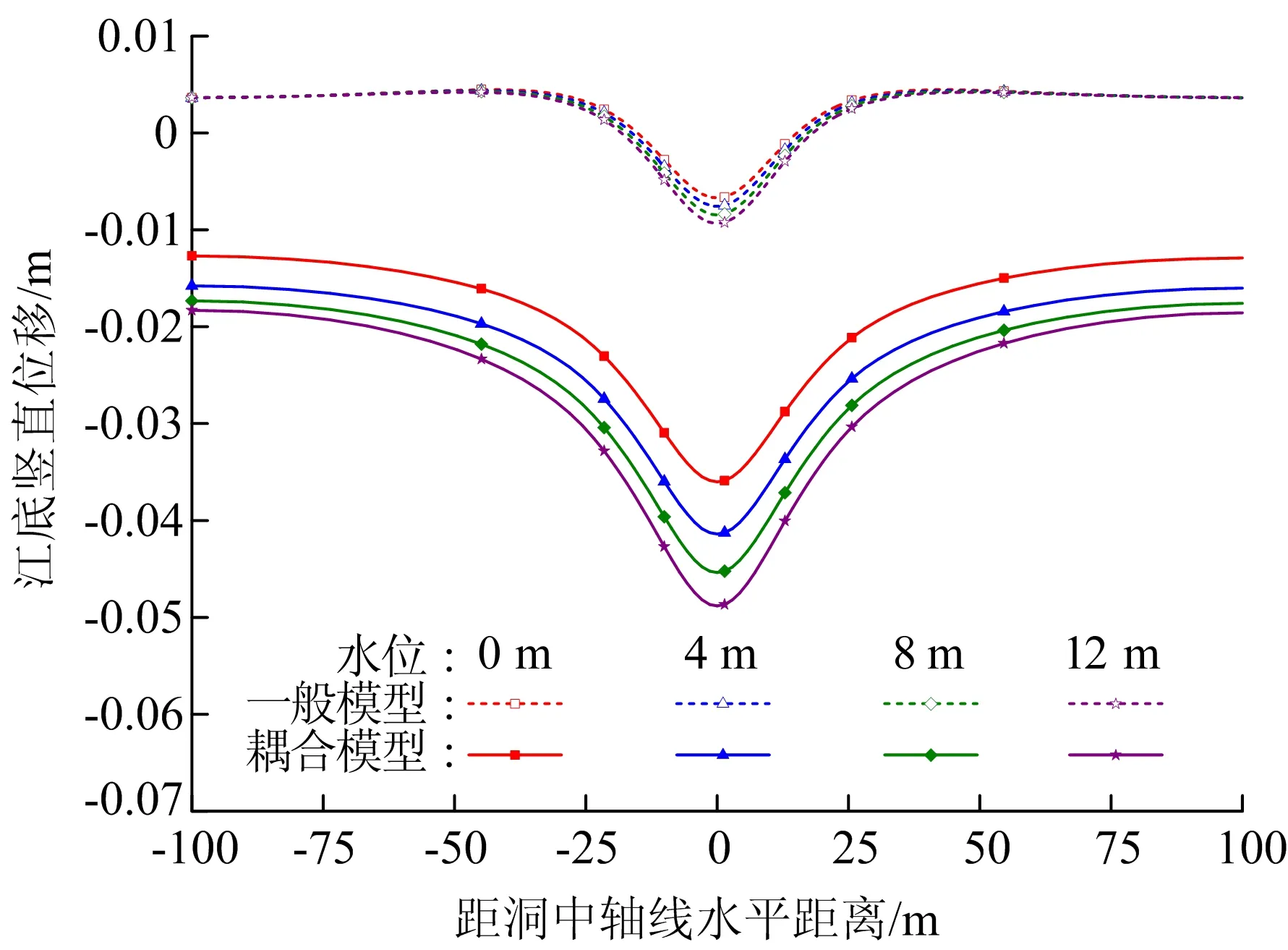
图7 不同江水位下江底竖直变形2种模型结果对比

由图7可知,不考虑水力耦合过程时,仅靠近隧道中轴线区域江底地面产生沉降,远离隧道区域地面发生少量隆起,江水位为0、4、8、12 m时,江底地表沉降最大值分别为0.006 7、0.007 6、0.008 5、0.009 4 m,地表隆起最大值分别为0.004 5、0.004 4、0.004 3、0.004 2 m,江水位变化引起的沉降增幅不超过0.003 0 m。考虑水力耦合过程时,江底地面沉降明显,无隆起现象,隧道中轴线处江底地面沉降最大,在0 m江水位时为0.036 m,12 m江水位时为0.049 m,江水位变化引起的增幅达0.013 m。由此可见,江水渗流作用对江底地面沉降变形影响很大,且随着江水位增大,影响效应更加明显,实际分析中考虑水力耦合效应非常重要。耦合模型很好地揭示了泥水平衡盾构掌子面发生漏水等问题时隧洞开挖施工将产生过大变形的安全隐患,可为工程施工过程制定安全应对措施提供依据,而基于一般模型的研究结果会导致对相关问题产生偏危险的判断,不利于应对措施的制定。

3.4 初始微裂纹分布对隧道开挖响应的影响

岩体力学特性和渗透性受内部初始微裂纹分布影响,受长期地质作用影响,岩体内部微裂纹结构复杂。在3.1—3.3节分析中,岩体内部微结构均假定呈各向同性分布,而实际穿江隧道某些区段围岩内部微结构可能优先沿某一方向分布。下面针对情形2,主要研究初始微裂纹优先呈水平与垂直分布2种情况。

受初始微裂纹优先水平或垂直发育影响,岩体初始渗透性各向异性特征显著,沿微裂纹优势方向的渗透系数为1.5×10-7m/s,而垂直方向为1.0×10-9m/s。初始微裂纹各向同性、优先呈水平与垂直发育时,隧道开挖引起的江底地面竖直变形如图8所示。

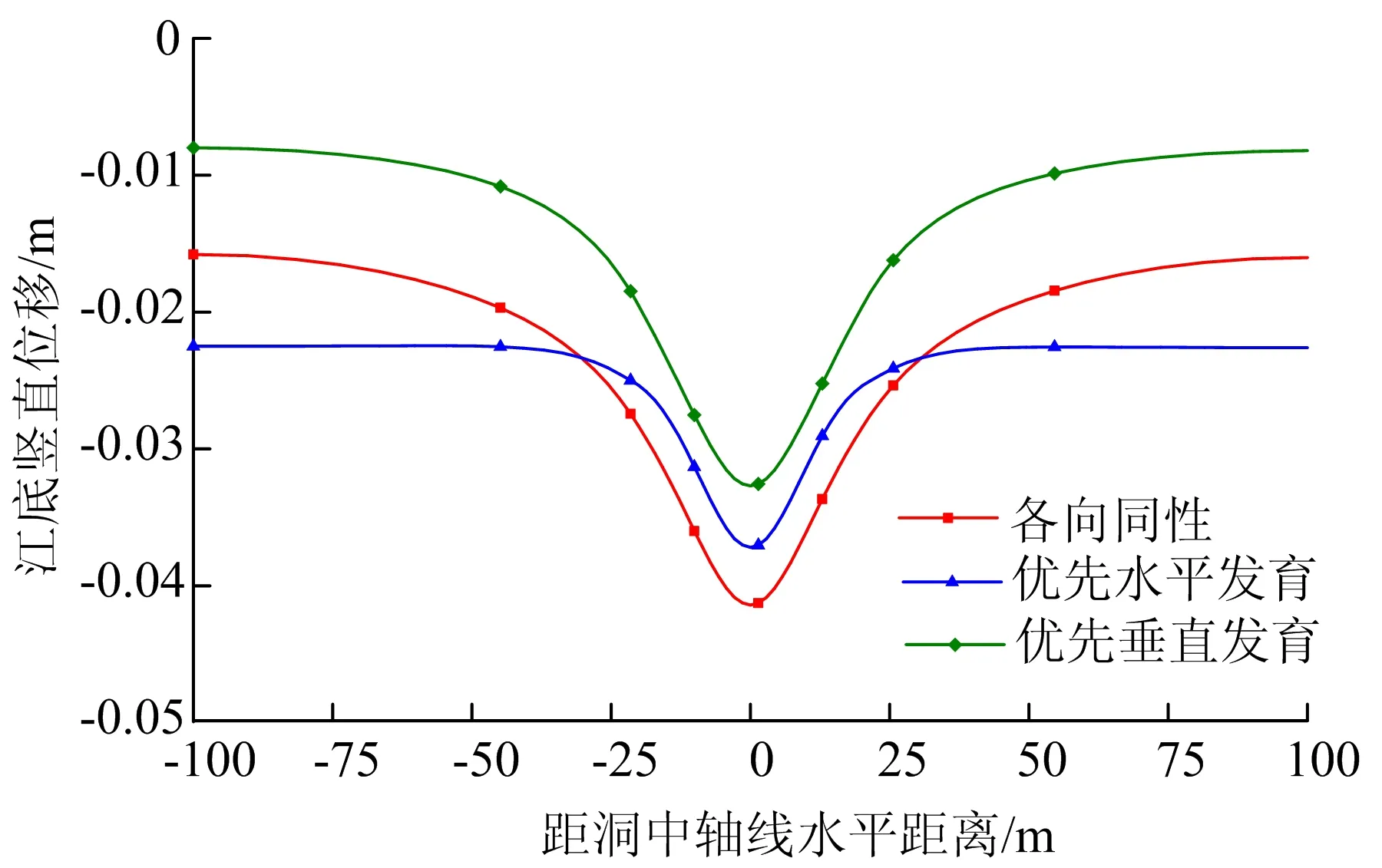
图8 初始微裂纹3种分布下隧道开挖引起的江底竖直变形

由图8可知,初始微裂纹分布特征对隧道开挖引起的江底地表变形响应影响较大。微裂纹优先垂直发育时,隧道开挖引起江底地表竖直沉降变形呈抛物线分布,与各向同性情况时规律一致,但沉降值变小,最大沉降值为0.032 7 m。与初始微裂纹呈各向同性分布的结果相比,优先水平发育时,江底地表竖直沉降最大值减小,为0.037 2 m,但在距离隧道中轴线2倍洞直径区域,竖直沉降增大,隧道开挖引起的江底地表沉降范围扩大。

初始微裂纹优先呈水平和垂直发育时,开挖隧道周围水压力分布如图9所示。

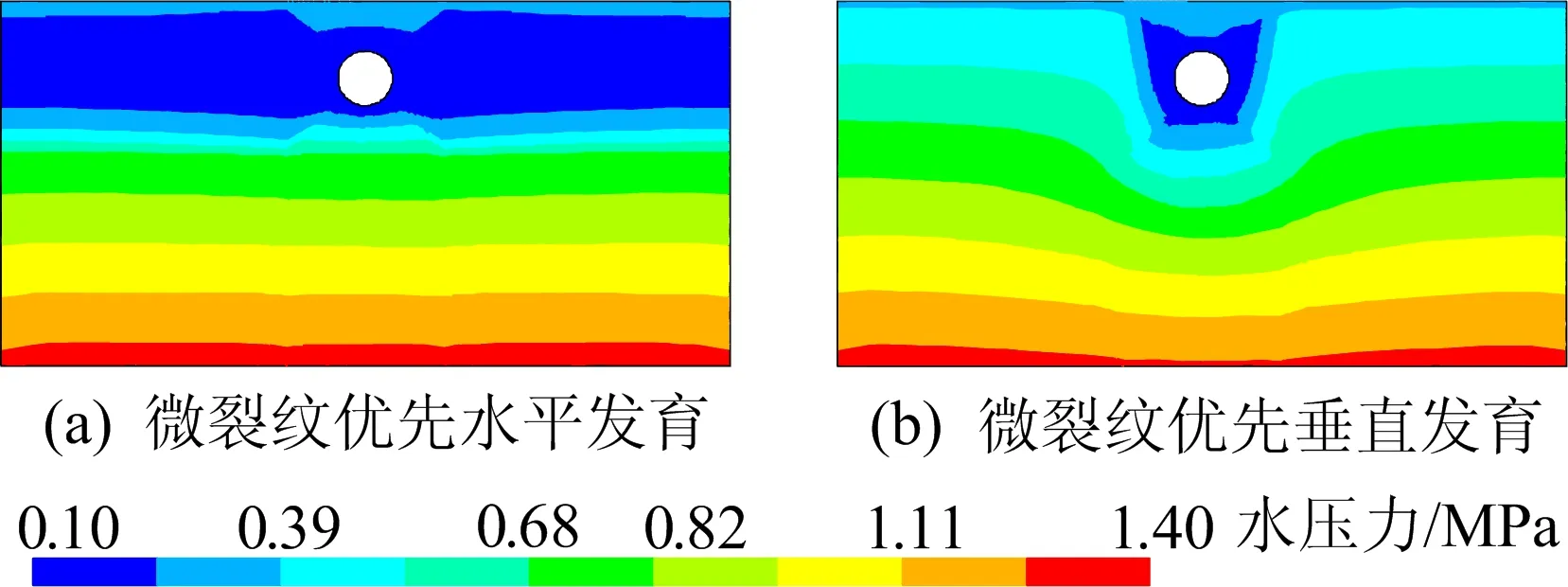
图9 初始微裂纹2种分布下开挖隧道周围水压力

由图9可知,微裂纹优先水平发育时,水压力降低区域明显增大,从而导致在距开挖隧道较远区域地表也产生较大的沉降变形。由此可见,初始微裂纹各向异性分布对江底隧道开挖引起的地表变形与水压力分布影响显著,岩体内部微裂纹等细观结构特征的准确表征对江底隧道开挖水力耦合响应模拟非常重要。

3.5 支护水压对隧道开挖响应的影响分析

泥水平衡盾构掌子面发生漏水问题时,穿江隧道开挖将导致江底产生非常大的变形,影响隧道围岩安全稳定。采用泥水平衡盾构进行穿江隧道开挖时,可通过对掌子面施加支护水压来减小对围岩的扰动。下面针对情形3,在支护水压分别为0.40、0.50、0.58、0.65 MPa时开展研究。不同支护水压下,采用2种模型计算隧道开挖引起的江底竖直变形结果如图10所示。

图10 不同支护水压下2种模型江底竖直变形结果

由图10可知,支护水压对江底隧道开挖引起的地表变形响应影响较大。不考虑水力耦合过程时,施加支护水压将引起江底地面产生隆起,且最大隆起值随支护水压增大而变大,但支护水压变化引起的江底地面位移变化幅度较小,最大变幅不超过0.006 m,据此无法有效进行适宜支护水压的确定。考虑水力耦合过程时,支护水压对控制江底地面变形的作用显著,无支护水压时,隧道中轴线江底最大沉降为0.041 m,0.40 MPa支护水压时减小为0.010 m,0.50 MPa支护水压时减小为0.001 m;支护水压为0.58、0.65 MPa时江底地面产生明显隆起,最大隆起值分别为0.007、0.010 m。由此可见,泥水平衡盾构掌子面支护水压可有效控制隧道开挖对周围岩体的扰动,采用耦合模型可有效确定适宜的支护水压,即隧洞顶部水压力为0.50 MPa。

4 结 论

1) 开挖隧道围岩变形同时受隧道开挖与江水渗流作用的影响,仅考虑隧道开挖作用时,洞周变形集中发生在隧道周围,洞底隆起明显大于洞顶沉降,同时考虑江水渗流作用后,隧道江底地表也产生较大的水平位移,洞顶沉降显著增大至不考虑水力耦合情况的3倍左右,洞底隆起明显减小,约比顶部沉降小1个数量级,随着江水位增大,渗流作用对开挖隧道变形的影响更加明显。

2) 隧道开挖引起的江底沉降随江水位增大而增加,受水力耦合作用影响显著。不考虑水力耦合时,江底地表沉降不超过0.010 m,考虑水力耦合过程后,江底地面沉降明显,0 m江水位时达0.036 m,12 m江水位时达0.049 m,表明实际分析中考虑水力耦合效应非常重要。

3) 隧道开挖引起的地表沉降与水压力响应受岩体内部结构特征的影响,初始微裂纹优先水平发育会导致水压力降低区域明显增大,在距开挖隧道较远区域地表产生较大的沉降变形。

4) 泥水平衡盾构掌子面支护水压可有效控制隧道开挖对周围岩体的扰动,随着支护水压增大,隧道中轴线江底地面沉降逐渐减小,但过大支护水压会引起地面显著隆起,适宜的支护水压为隧洞顶部水压力0.50 MPa。

在实际江底隧道开挖施工过程中,应特别关注江水渗流对江底与围岩变形的影响,宜在低江水位情况下施工,同时需保证盾构掌子面支护水压的合理施加,并防止因漏水等问题引起隧道围岩产生过大变形,影响隧道安全稳定。