基于佳点集人工鱼群的点云配准算法

李书群, 陈 钰, 杨雨婷, 余 敏, 朱勇超, 屈小川

(1.合肥学院 城市建设与交通学院,安徽 合肥 230601; 2.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 3.合肥工业大学 管理学院,安徽 合肥 230009)

0 引 言

三维激光扫描技术诞生于20世纪90年代,它通过高速激光扫描测量的方法大面积、高分辨率地快速获取被测对象表面的三维坐标数据,即点云数据集[1]。该技术虽然已经广泛应用于变形监测、古建筑保护、智慧城市等多种现代化领域内[2],但是在实际生产过程中,由于目标物规模过大,采集目标物的三维点云数据往往需要多角度、多方位扫描,再通过拼接各个点云数据集以得到完整的目标物体三维点云数据。点云数据拼接的关键是点云配准,该技术在医学影像[3]、逆向工程[4]等领域有重要作用。点云配准又分为粗配准和精配准。目前广泛应用的点云精配准迭代最近点(iterative closest point,ICP)算法[5],对待配准点云数据集的初始位置姿态要求较高,较大的旋转会导致在迭代过程中需要重复搜索最近邻点,影响配准精度[6]。因此,许多粗配准算法被相继提出,如四点一致集(4-points congruent sets,4PCS)算法[7],该算法虽配准速度较快,但对于平面较大而其他特征不明显的点云容易配准失败。

为提高配准效率,文献[8]提出三维正态分布变换(3D-normal distributions transform,3D-NDT)算法,相比ICP算法,该算法不需要重复计算最近邻点,效率更高,然而该算法依赖于配准矩阵初值。除此之外,基于群智能算法理论的方法在三维点云配准中也得到了广泛应用,如基于布谷鸟优化的三维点云配准算法[9]、基于曲率信息的人工蜂群算法[10]等。虽然这类算法能较好地为精配准提供好的初始位姿,但是仍然存在寻优时间较长、收敛速度较慢的缺点。

因此,需要设计一种算法,对目标函数的性质、初值、参数设定的要求不高,有较大的容许范围,且具有寻优速度较快、具备全局寻优、收敛速度快等优点。文献[11]提出了一种基于鱼类动物行为的群体智能优化算法,可以满足上述要求,但该算法中人工鱼的初始位置是随机产生的,易陷入局部最优;文献[12]采用佳点集(good point set,GPS)理论对种群初始化有助于增加种群的多样性,提升了算法的收敛速度。

针对以上问题,本文提出一种基于佳点集人工鱼群的点云配准算法。首先选择人工鱼群算法,采用佳点集理论实现人工鱼群中人工鱼位置的初始化,避免陷入局部最优;然后将待配准的两片点云的对应点距离的均方根作为适应度函数,以均方根最小作为本文算法的寻优准则,利用该算法对点云配准中刚性变换矩阵的6个参数进行全局寻优;最后通过寻优得到参数计算刚性变换矩阵,实现两片点云的粗配准,从而为ICP精配准提供良好的初始位姿。

1 佳点集人工鱼群算法原理

1.1 人工鱼群算法

人工鱼群算法是一种模仿鱼群觅食、聚群、追尾行为的群体智能优化算法。通过模拟鱼群的觅食过程,由觅食行为、聚群行为和追尾行为来构造寻优策略,从而达到全局寻优的目的。该算法具有全局搜索能力强、鲁棒性强等优点。

给定某一区域内N条人工鱼,第i条人工鱼在D维空间状态为xi=(xi,1,xi,2,…,xi,D),i=1,2,…,n。该区域内N条人工鱼的状态均随机生成,人工鱼的适应度函数为Y=F({xi|i=1,2,…,N}),包括以下参数:种群规模N、人工鱼视野visual、步长step、拥挤度因子δ、尝试次数trynumber、最大迭代次数L、随机数Rand(0,1)。算法描述[13]以求解适应度函数最大值为例,标准人工鱼群优化算法可描述为:

1) 觅食行为。在当前人工鱼xi的感知范围内随机选择某一状态xj,其适应度函数为Yj,若优于当前人工鱼状态,向该方向移动1步;若达到尝试次数后仍不满足条件,则随机移动1步。

2) 聚群行为。计算当前人工鱼感知范围内人工鱼的数目nf及其中心位置Xc。若Yc/nf>δYi,说明该位置食物浓度较高且不拥挤,向该方向移动1步;否则执行觅食行为。

3) 追尾行为。搜索当前人工鱼视野范围内状态最优的人工鱼Xmax,若Ymax/nf>δY,向该方向移动1步;否则执行觅食行为。

4) 公告板。记录最优的人工鱼状态。

1.2 佳点集理论

1.3 佳点集人工鱼群算法

合理分布的初始种群有助于算法性能的提升和更好地进行全局寻优。然而,标准人工鱼群算法的种群由随机初始化方法得到,易因初始种群分布不均而陷入局部最优。针对此问题,受佳点集理论的启发[14],在算法中采用指数序列rk={ek,1≤k≤s}初始化种群。本文采用随机方法和指数序列方法生成的二维初始种群分布对比如图1所示,从图1可以看出,通过指数序列法生成的初始种群分布均匀,能避免因种群初始分布不均造成人工鱼群算法陷入局部最优,因此本文采用指数序列方法生成佳点集,从而完成人工鱼群算法种群的初始化。

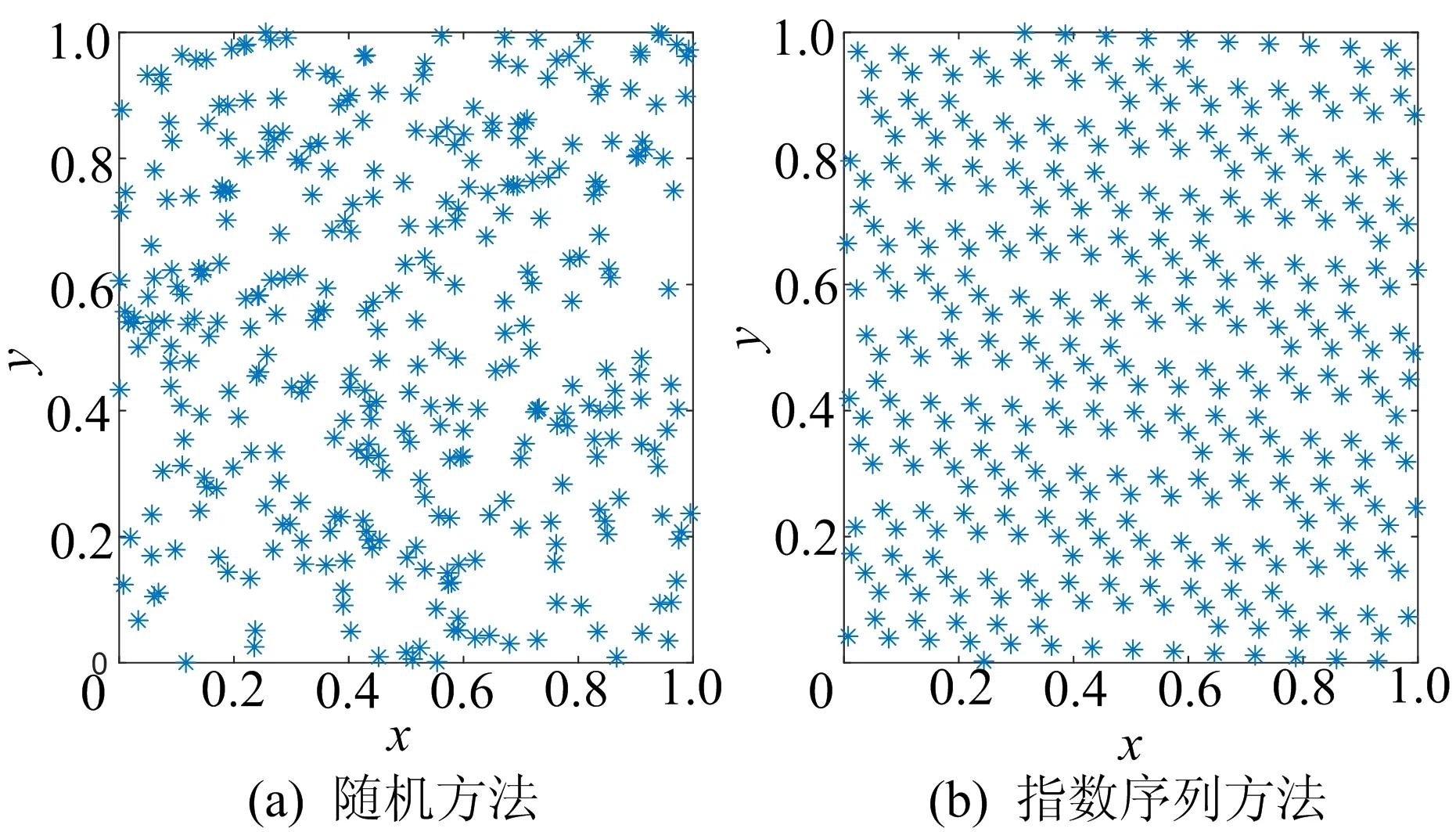
图1 2种方法生成的种群分布对比

本文采用3种测试函数(Ackley、Rastrigin、Rosenbrock函数)对标准人工鱼群算法和佳点集人工鱼群算法的性能进行测试。算法参数设置为:人工鱼数N=80,人工鱼维度D=6,最大迭代次数Tmax=500。测试结果如图2所示。

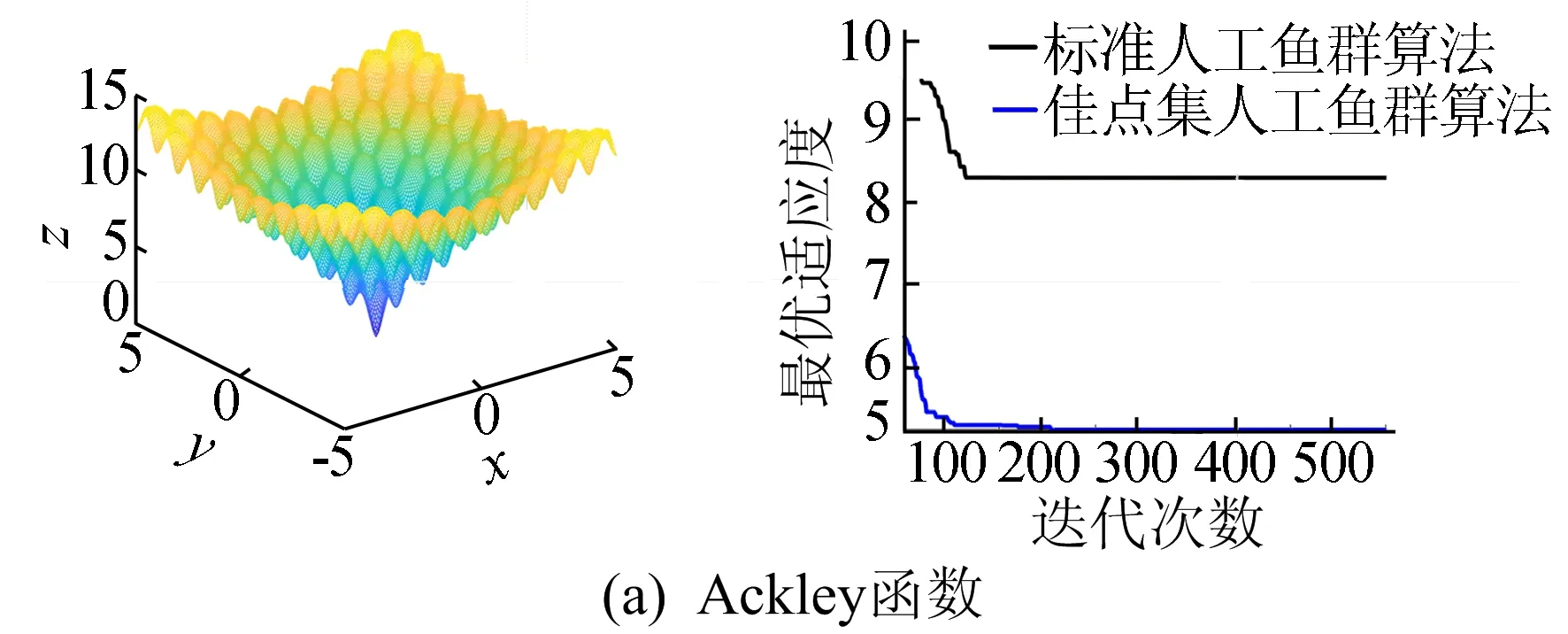
图2 2种算法在不同基准函数下的适应度对比

从图2可以看出,经过佳点集优化后的人工鱼群算法相比标准人工鱼群算法的寻优精度更高,在3种测试函数下的收敛精度分别提高了约1、3、10倍。

2 基于佳点集人工鱼群算法的点云配准

2.1 点云配准算法

现有激光点云的配置工作,首先需要保证点云数据能够统一到同一坐标系下,即进行点云配准。该源点云P={pi,i=1,2,…,s},目标点云Q={qj,j=1,2,…,t}。s、t分别为P、Q中点的数量。

点云配准问题的本质是通过寻找到刚性变换矩阵T的6个参数,即坐标轴的平移量(Vx,Vy,Vz)和坐标轴的旋转角(α,β,γ),使得两组点云数据的对应点经过空间变换后尽可能重合,即2个点云集对应点对的距离差平方和最小。刚性变换矩阵的表达方式为:

(1)

由于点云数据本身的测量误差、采样密度等因素的影响,两组点云数据经过空间变换后,对应点的距离平方差和无法达到理想欧式距离0。因此,点云配准可以表述为全局最优化问题,即寻找最优刚性变换矩阵T,使得2组点云数据的对应点的距离差平方和最小,即

(2)

结合佳点集人工鱼群算法,将对应点的均方根误差(root mean square error,RMSE)数值作为适应度函数进行全局搜索,RMSE的计算公式如下:

F(T)=RMSE(P,Q)=

(3)

其中:S为两片点云的匹配点个数;pi为点云P中与qj匹配的点的坐标;RMSE(P,Q)为两片点云对应点距离的均方根误差,其值越小,代表配准精度越高。

2.2 点云下采样与特征点提取

由于点云数据的数据量大,为加快配准过程中的计算速度,提升运算效率,本文采用体素栅格法对点云数据进行下采样。体素栅格采样将原始点云进行体素划分,将每个体素内的重心点P′作为下采样点。经过采样后,点云数据得到简化。

为了进一步提高待配准点云数据在匹配点处的稳定性和速度,采用三维尺度不变特征变换(3D scale invariant feature transform,3D SIFT)特征点提取算法对下采样后的点云进行特征点的提取。

设经过下采样后的点云数据有N个点,任意一点的坐标为pi=(xi,yi,zi),i=1,2,…,N,k为尺度调整参数,σ为空间尺度参数,S为高斯金字塔每组层数。计算步骤如下:

1) 将三维高斯函数与点云进行卷积,计算其尺度空间L(x,y,kσ)。

G(x,y,z,kσ)=

(4)

L(x,y,kσ)=G(x,y,kσ)⊗p(x,y,z)

(5)

2) 计算相邻尺度层的高斯差分模型,其中i∈(0,S+2)。

DOGi=L(x,y,z,kσ)-Li-1(x,y,z,kσ)

(6)

3) 计算DOG函数空间上的极值点,将该极值点P″作为3D SIFT特征点。

利用3D SIFT特征点可以对点云的局部空间关系进行更准确地描述,也能在特征点附近建立更为稳定的对应关系。

2.3 错误对应关系的剔除

通过将源点云P和目标点云Q进行下采样及3D SIFT特征点提取后的点云P″和Q″,使用快速点特征直方图(fast point feature histogram,FPFH)进行局部特征描述[15]。根据P″的FPFH特征,查找Q″中与该特征相似的点作为匹配点对。由于点云数据中存在局部形态相似、噪声情况,实际匹配过程中会出现许多错误的对应关系,造成配准误差,影响人工鱼群寻优的效率,本文综合距离阈值、随机采样一致性(random sample consensus,RANSAC)模型、法向量夹角3种方法剔除错误对应关系,以提高算法寻优效率。

2.3.1 基于距离阈值

在通过FPFH特征得到匹配点对后,可以计算出匹配点对的欧氏距离。当对应点对的距离大于设置的距离阈值εd时,认为该对应点对为错匹配点对并剔除该对应关系[16]。

2.3.2 基于RANSAC模型

RANSAC方法[17]通过在全局范围内对待匹配对象和场景对象进行随机采样,由随机采样最小的n个样本,得到初始参数模型,在包含异常点的样本集中迭代验证初始模型;在该验证过程中,计算待验证样本点与初始模型的误差,小于设置的阈值归为内点;否则标记为外点。本文通过设置距离阈值εransac和迭代次数iter,将点云P″和Q″作为RANSAC模型的输入,进行迭代。迭代完成后,认为外点的对应点对为错匹配点对并剔除该对应关系。

2.3.3 基于法向量夹角

虽然通过距离阈值和RANSAC模型进行错误匹配关系的剔除,但仍存在一部分错误匹配关系。匹配点对的空间拓扑关系大概一致,因此本文基于匹配点对的法向量夹角进行错误对应关系的剔除。由于在点云数据密集处,并且搜索半径不大情况下,每个点的法向量可以用局部拟合平面的法向量表示[18],方法如下:

1) 选择M点最近的k个点,通过Kd-tree进行邻近点搜索,确定M点的邻近点集W={wi,1≤i≤k},设V为点集W的重心,L为过点M平面的法向量。通过对M的邻域使用最小二乘法进行局部拟合平面,使得下式最小。

(7)

式(7)最小值的解可以通过求由最小二乘得到的矩阵C的最小特征值对应的特征向量[19]。

(8)

2) 计算经过RANSAC模型剔除后的对应点对的法向量夹角θ。

3) 当θ大于设定的阈值εθ时,则认为对应点对为错匹配点对并剔除该对应关系。

2.4 佳点集人工鱼群点云配准算法步骤

1) 设置算法的相关参数。

2) 对待配准的点云进行下采样得到P′,利用3D SIFT特征点提取算法对采样后的点进行特征点提取得到P″。

3) 基于佳点集初始化N条人工鱼的初始位置。

4) 使用由人工鱼的位置生成的刚性变换矩阵T对P″进行平移旋转得到T(P″)。

5) 通过FPFH特征描述获得T(P″)和Q″的对应关系并剔除错误对应关系,将剔除错误对应关系后对应点距离的均方根误差作为适应度函数初值,并更新公告板。

6) 每条人工鱼分别执行觅食、聚群、追尾行为,更新公告板和每条人工鱼的适应度值。

7) 循环步骤4)～步骤6),达到最大迭代次数Tmax或2次适应度值小于设定的阈值后,输出公告板结果。

佳点集人工鱼群点云配准算法流程如图3所示。

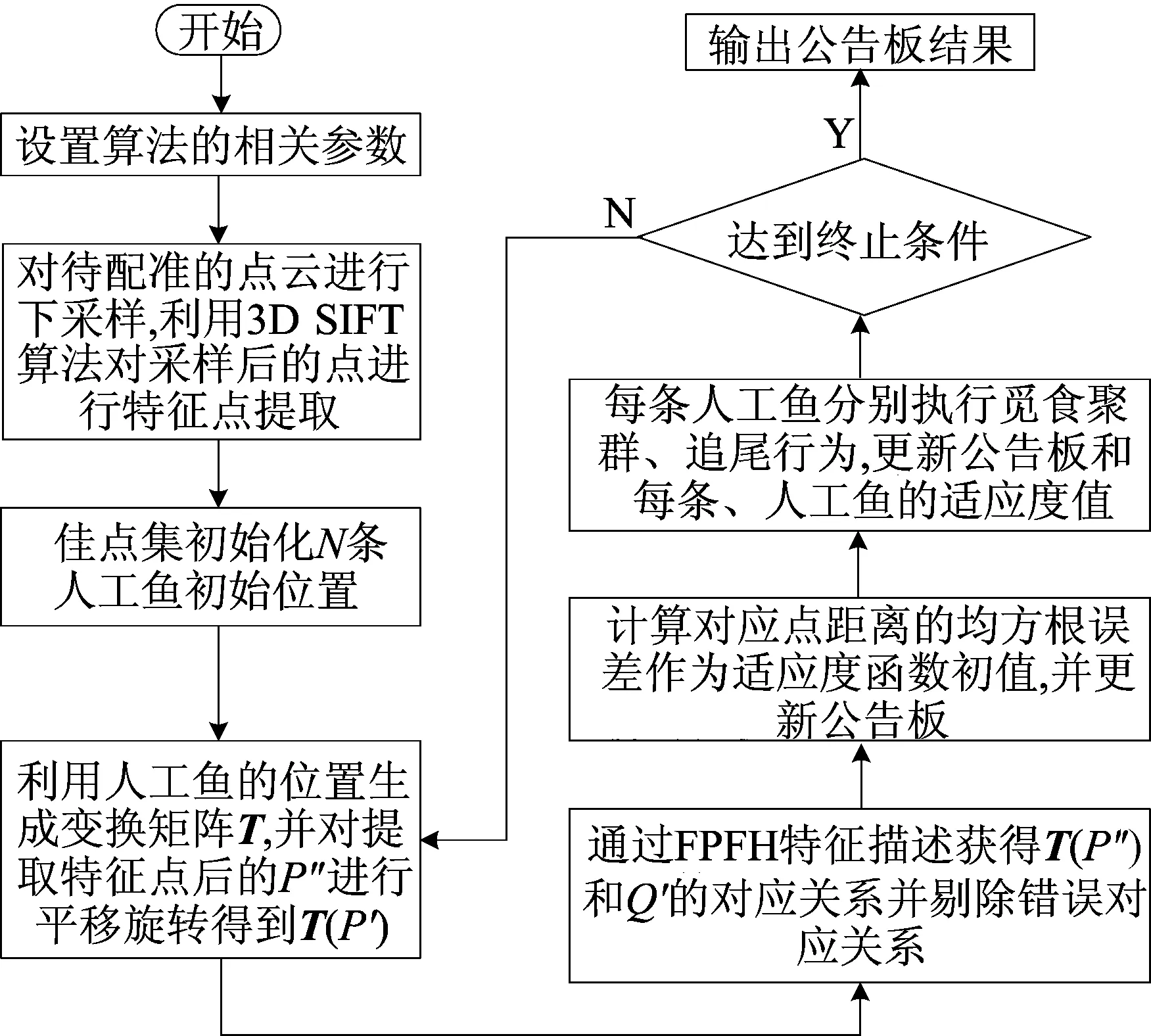
图3 佳点集人工鱼群点云配准算法流程

3 实验结果及分析

实验环境设计的代码均采用C++编写,使用open-source point cloud library(PCL)开源库1.11.1,编译器为Microsoft Visual C++(MSVC) 14.27,未开启编译优化。计算机硬件配置为Intel Core@ i5-8400处理器,2.80 GHz CPU,16 GiB内存,操作系统为Windows 10。

为了验证本文基于佳点集人工鱼群算法在点云配准过程上的有效性,首先设置算法的各项参数:种群规模N为5,移动步长step为0.005,尝试次数trynumber为2,视野visual为0.15。由于本文算法局部最优不严重,忽略拥挤度因子δ。人工鱼群最大迭代次数Tmax为15。平移量范围为[-0.04,0.04]m,旋转角度范围[0°,360°]。

3.1 点云库模型数据

本文的实验数据包括斯坦福大学经典的Bunny、Dragon、Happy Buddha数据集,如图4所示。其中:Bunny数据集选用bun-zipper点云;Dragon数据集选用dragonUpRight-0视角的点云;Happy Buddha数据集选用happyStandRight-0视角的点云。

图4 实验测试数据集

实验过程中,选取模型中的点云作为源点云数据集,目标点云则通过设置一组平移旋转参数将源点云中的点通过空间变换得到,空间变换后数据集的大小不变。点云数据集大小见表1所列。

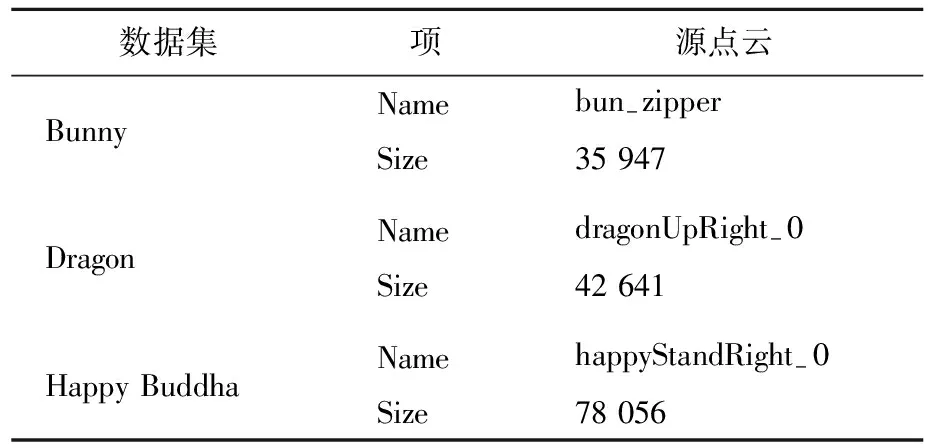
表1 点云数据集

3.2 实验结果

为了验证本文提出的基于佳点集人工鱼群的点云配准算法的性能,本文对ICP算法与本文算法+ICP算法进行了对比实验。实验过程数据见表2所列,配准后的配准实验对比如图5所示。表2中:平移参数Vx、Vy、Vz为沿坐标轴进行平移的数值,单位为m;旋转角度α、β、γ为沿坐标轴进行旋转的角度大小,单位为 °;t1为本文算法配准时间;t为使用ICP算法配准时间;t2为经本文算法粗配准后使用ICP算法配准的时间;RMSE-coa为本文算法粗配准精度,RMSE-fin为经过粗配准后使用ICP算法精配准的精度。其中ICP算法设置最大迭代次数200次,同时为了配准精度,ICP算法迭代过程中不设置下采样。

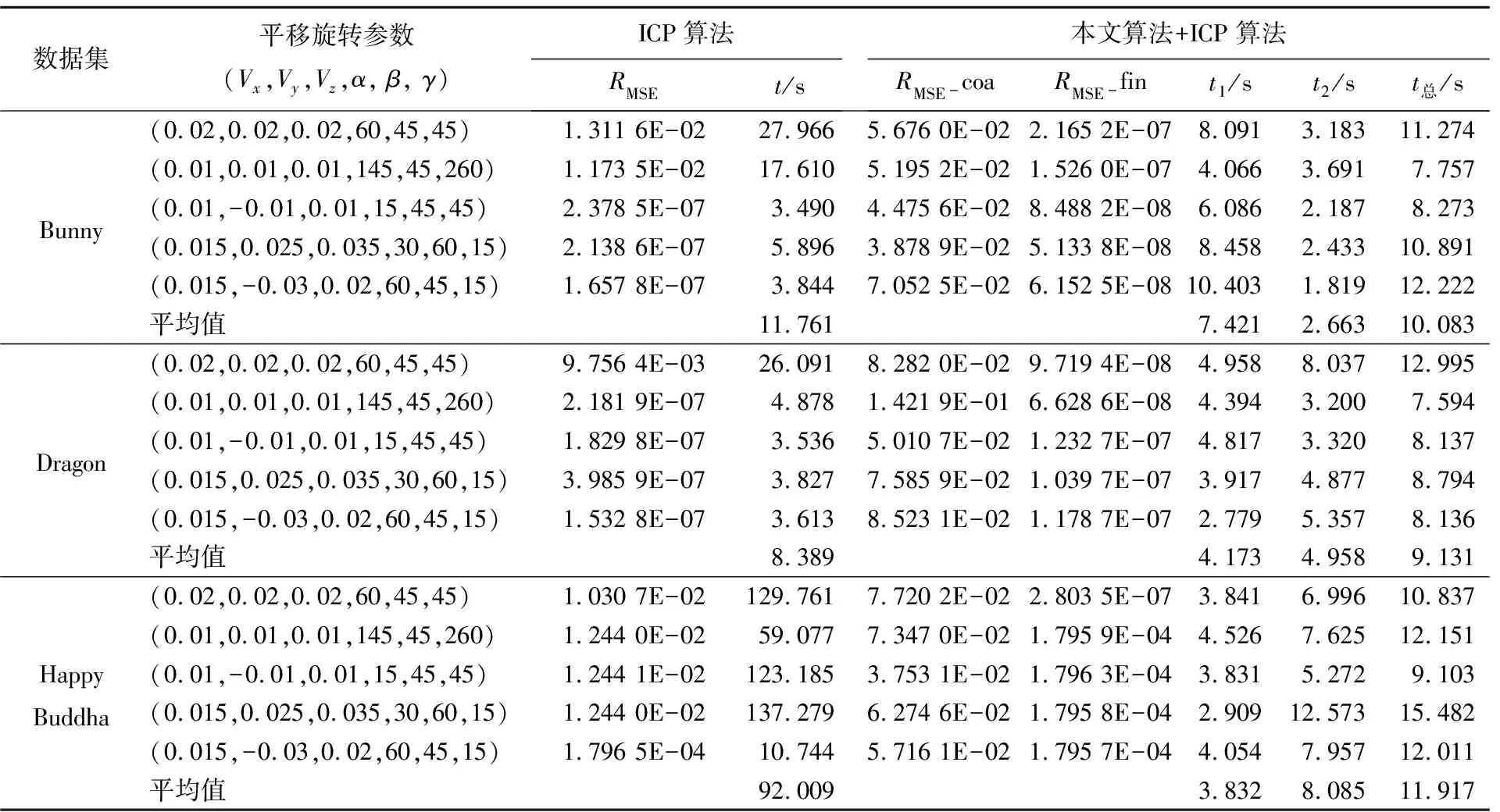
表2 3种数据集按不同算法配准的时间与精度

图5 传统的ICP算法与本文算法+ICP算法的配准实验对比

由表2可知:ICP算法对于初始位姿较好的点云,配准精度尚可,但初始位姿不好的情况下,易陷入局部最优,配准时间显著增加,甚至配准失败;而本文算法通过为ICP算法提供一个良好的初始位姿,在达到同等精度或更高精度的情况下,能减少ICP算法的配准时间;Bunny、Dragon、Happy Buddha点云数据集经过本文算法粗配准后再使用ICP算法配准,平均分别耗时2.663、4.958、8.085 s;相比直接使用ICP算法分别减少9.098、4.216、83.924 s。

在(0.02,0.02,0.02,60,45,45)这组平移旋转参数下,Bunny、Dragon、Happy Buddha点云数据集采用本文算法+ICP算法比直接使用ICP算法的配准精度提高了5个数量级,配准时间分别减少16.692、13.096、118.924 s。而对初始位姿尚可的点云,采用本文算法+ICP算法比直接使用ICP算法进行配准,Bunny和Dragon数据集的配准时间平均约增加5 s,Happy Buddha数据集的配准时间平均约增加2 s,而其精度提高了1个数量级。

采用(0.02,0.02,0.02,60,45,45)这组平移旋转参数得到目标点云,使用本文算法对Bunny、Dragon、Happy Buddha 3组数据集进行迭代。迭代寻优过程中的对比如图6所示。

图6 迭代次数曲线

从图6可以看出,本文算法只需要迭代4次左右就能实现均方根误差收敛。

4 结 论

本文利用佳点集改进人工鱼群算法中种群初始化行为,增加了种群的多样性,克服了基本人工鱼群算法因初始种群分布不均易陷入局部最优的缺陷,并将该算法运用到点云配准过程中,提出了基于佳点集人工鱼群算法的点云配准算法。通过采用取斯坦福大学提供的3组数据集进行由粗到精的配准实验,并与ICP算法进行比较,发现本文算法对于初始位姿不好的点云,能避免传统ICP算法因初始点云旋转角度过大而配准失败,配准精度可以提高5个数量级,同时缩短配准时间,进而表明本文算法具有较好的有效性与可靠性。