基于法矢量修正和参数修正的点云双边滤波改进算法
2023-10-10梁敏萱李英博强晶晶谷琼琼陈蕙心
梁敏萱,李英博,强晶晶,谷琼琼,陈蕙心
(上海无线电设备研究所,上海 201109)
0 引言
激光三维成像雷达可以获取三维立体图像,同时具有较强的目标识别能力及低功耗、低成本的优点,逐渐被应用于军事、民用和科学实验领域。但是在实际点云数据采集过程中,受天气、环境和设备本身测量误差的影响,会引入噪声。为了最大程度发挥激光三维成像雷达的优势,需要对其采集的点云数据进行滤波处理。
点云滤波能够在消除噪声的同时很好地保留目标的特征信息。从20世纪90年代开始,国内外科研人员已经围绕点云滤波开展了大量的研究,近些年来更是精益求精,提出了很多先进的点云滤波技术。SCHALL 等[1]受均值漂移技术的启发,利用迭代策略将点移动到高概率的位置,采用基于核的聚类滤波方法实现了点云滤波,但是该方法会导致目标特征信息丢失严重。DUAN等[2]提出了一种基于主成分分析(principal component analysis,PCA)的自适应聚类方法,该方法计算复杂度较低,在有效去除噪声的同时保留了环境细节特征,但是需要人为设置多个阈值。FLEISHMAN 等[3]和JONES等[4]将图像双边滤波应用到三维点云数据处理中,提出了点云双边滤波算法。该算法鲁棒性强,具有良好的降噪能力,但是对点云尖锐区域特征保留程度有限。焦亚男等[5]利用半径滤波处理离群孤立点,将改进的具有噪声基于密度的聚类(density-based spatial clustering of applications with noise,DBSCAN)算法和八叉树结构相结合,建立点云间的拓扑关系来滤除小尺度噪声,但是该算法计算复杂度非常高。黄五超等[6]提出基于r邻域的点云去噪算法,采用最大距离阈值区分信号点与噪声点。朱广堂等[7]基于移动最小二乘曲率特征进行点云去噪,通过判断曲率与设定阈值的关系来去除噪声点,但是该算法的鲁棒性不强。
针对现有点云滤波算法对目标特征信息保留程度不高以及人为参与因素过多的问题,本文提出一种基于法矢量修正和参数修正的点云双边滤波改进算法。该算法利用加权的主成分分析法进行法矢量估计,并基于邻域点的影响对法矢量进行修正,最后对双边滤波因子中的高斯核函数参数进行修正。
1 算法原理
1.1 点云双边滤波
点云的双边滤波算法由图像的双边滤波算法发展而来。在二维图像处理中,双边滤波算法是用第i个数据点pi的k邻域点加权平均的灰度值来取代原始数据点的灰度值,从而达到去除噪声的目的。在点云中,双边滤波可以简单地理解为在点云法线方向上对点的位置进行修正。点pi修正后的位置矢量
式中:pi为点pi当前的位置矢量;α为双边滤波因子;ni为点pi当前的法矢量。双边滤波因子α的计算公式为
其中
式中:pij为点pi的第j个邻域点pij的位置矢量;k(pi)为点pi邻域点的位置矢量集;Wc(·)为空间域权重函数,用以控制平滑程度;‖·‖为矢量的二范数运算符;Ws(·)为特征域权重函数,用以表明邻域点间法矢量的变化;〈·〉为矢量内积运算符;nij为点pi的第j个邻域点的当前法矢量;σc,σs分别为距离权重因子与特征保持因子。
1.2 加权主成分分析法估计法矢量
点云法矢量是点云表面形状的重要特征参量,是描述物质表面走向的矢量。因此准确估计点云法矢量有助于保留点云模型的详细特征,并为点云分割和目标识别提供基础数据。利用主成分分析法估计点云法矢量的步骤如下。
步骤1,读取点云数据集合及邻域数据集合。设给定数据点pi的坐标为(xi,yi,zi),其中i=1,2,…,N,N为点云数据集合中数据点的总个数。则点云数据集合P可以表示为
以数据点pi为中心,建立其k邻域拓扑关系,数据点pi的k邻域数据集合
式中:(xij,yij,zij)为pi第j个邻域点pij的三维坐标。
步骤2,对于数据点pi,利用最小二乘法对其k邻域内的所有点拟合局部最优平面,即最小化邻域内所有的数据点到目标平面的空间距离。以此构建目标函数
式中:n为局部最优平面的法矢量;d为全局坐标原点到局部最优平面的空间距离;argmin(·)为目标函数最小时自变量的取值函数。
步骤3,用最小二乘法拟合平面求法矢量,可以转换为利用主成分分析法求协方差矩阵最小特征值对应的特征矢量,即将求解式(7)转化为求解协方差矩阵Ci。Ci的求解公式为
式中:表示数据点pi邻域内所有点位置的均值,即重心位置矢量;T 为矩阵转置运算符;λm和em分别表示协方差矩阵Ci的特征值和其对应的特征矢量,且λ0≤λ1≤λ2。最小特征值λ0对应的特征矢量e0就近似为数据点pi的法矢量。
传统的主成分分析法在利用拟合局部最优平面方法估计法矢量时,对k邻域内的所有点赋予同样的权重。该加权方式对平坦面法矢量的估计影响不大,但因忽略了复杂曲面等特殊条件下点云分布的差异,会导致复杂曲面的点云法矢量估计结果失真。REN 等[8]将邻域点权重引入主成分分析法中,使改进的主成分分析法能够准确估计点云的法矢量和特征值,从而保证后续滤波能够取得良好的效果。
随机选取点云数据中的数据点pi,用dj表示点pi与其第j个邻域点pij之间的距离,则pij的权重wj可以表示为
计算邻域点位置矢量的加权平均
根据式(10),加权协方差矩阵
空间距离越近的点,其几何特征越相似。这种加权方法更重视距离当前点pi更近的邻域点的影响,而减小了较远的邻域点对法矢量估计的干扰,提高了曲率变化较大的点云法矢量估计的鲁棒性。
1.3 法矢量修正
基于加权主成分分析法估计点云法矢量具有二义性,该方法只能确定法矢量所在直线,而无法确定其方向。假设点云中点的数量足够多且采样平面处处光滑,那么相邻两点的法矢量会接近于平行[9]。令ni和nj分别为相邻两点pi和pj的法矢量,如果ni·nj<0,说明两个法矢量的方向不一致,则将nj翻转,以此对求出的法矢量进行重定向。
协方差矩阵各特征值对应的特征矢量为基矢量,而基矢量的各个维度下信息的丰富程度与特征值线性相关,所以可以用最大特征值对应的特征矢量来确定多维数据的主成分。主成分分析法就是通过删除一部分分辨率较低的数据来实现降维。虽然主成分分析法在计算法矢量时有一定的抗噪能力,但是如果点云中存在离群点,法矢量估计的准确性将会受到很大的影响,因此需要对计算得到的法矢量进行修正。
将反映物体特征的点称为特征点,反之,则称为非特征点。文献[10]提出基于双边滤波的法矢量修正方法,修正的法矢量n′i的表达式为
其中
式中:G1(·)和G2(·)为高斯函数;σ1和σ2为高斯核函数超参数。
采用基于空间距离的加权主成分分析法可以降低离群点对法矢量估计的影响,但是该方法会影响特征点的法矢量估计。文献[10]综合考虑了空间距离和法矢量差异来实现对点云法矢量的修正。如式(13)所示,G2(‖nij-ni‖)用于描述法矢量之间的差异,G2(‖nij-ni‖)的引入可以降低加权主成分分析法对特征点矢量估计平滑作用的影响。‖nij-ni‖ 的值越小,意味着法线夹角越小、两个点的几何特征越相近。但文献[10]中的高斯核函数超参数是人为设置的。本文为了降低人为主观因素的影响,基于数据本身构造适应性的高斯核函数超参数,即
针对椅子部分点云数据,传统主成分分析法求得的未修正的法矢量如图1所示,加权主成分分析法求得的法矢量根据式(12)修正后的结果如图2所示。

图1 “椅子”点云未修正的法矢量

图2 “椅子”点云修正后的法矢量
由图1和图2可以看出,“椅子”点云修正后的法矢量明显比未修正的法矢量有序,更有利于后续双边滤波正确改变点云位置。
1.4 空间距离权重因子与特征保持因子的修正
空间距离权重因子σc反映的是待处理的数据点pi与其k邻域中点的距离对滤波的影响。σc越大,滤波后的模型越平滑,这也就意味着点云的细节特征将会被平滑。特征保持因子σs反映的是数据点pi与其k邻域中点的距离在法向上的投影对滤波的影响。σs越大,特征保持效果越好。目前传统点云双边滤波算法仍然需要根据点云数据,人为设定空间距离权重因子和特征保持因子。而本文利用局部特征权重和高斯核函数自适应设置双边滤波参数。
文献[11]中基于曲率信息计算数据点pi的k邻域局部特征权重wi的表达式为
其中
式中:Kij和Ki分别为邻域点pij和当前点pi的平均曲率;为所有点云的平均曲率。如果点云数据中的当前点pi的k邻域局部特征权重wi大于给定的阈值w0,则认为该点为尖锐区域点;否则,则认为该点为平坦区域点。文献[12]给出的权重阈值w0的表达式为
式中:wmin和wmax分别为所有点云数据的局部特征值中的最小值和最大值;t为通过实验得到的经验参数。
对于平坦区域的点云,可以通过增大σc来增加该区域的平滑效果,本文选取邻域点与当前点的最大距离作为σc。此时σs的作用不大,可以用当前点与邻域内各点法矢量的差异标量的标准差来表示。同理,对于尖锐区域的点云,可以通过减小σc来提高对细节特征的保留程度,本文选取当前点与邻域内各点法矢量的差异标量的最小值作为σs。此时σc的作用不大,可以用当前点与邻域内各点距离的标准差来表示。综上所述,σc和σs可分别表示为
式中:max(·)为最大值函数;|·|为绝对值运算符;min(·)为最小值函数。
综上所述,将经过修正的法矢量、空间距离权重因子和特征保持因子代入点云双边滤波算法中,即可得到改进的点云双边滤波算法。
2 实验验证
实验采用斯坦福大学公开数据集中的兔子模型,利用Matlab2017进行程序的编写,邻域范围取k=40。
2.1 空间距离权重因子与特征保持因子的选取
文献[13]利用点云的平均曲率分布计算当前点的局部熵,用于描述当前点所代表的局部曲面变分的有序程度。局部熵越大,该点所在局部区域的无序程度越高,该点提供的信息量越大,表征的细节特征越多。定义当前点pi的k邻域局部熵Hi为
其中
式中:qi和qij分别为当前点pi和其邻域点pij的平均曲率的分布概率。若点云总数量为N,则所有点云的熵
参考文献[12]和文献[14],根据σc和σs的特性可知,σc和σs分别有三种可能的取值,如表1所示。

表1 空间距离权重因子σc 和特征保持因子σs 的不同取值
文献[14]还提出了一种利用法向离群因子改进双边滤波算法的方法。本文利用全局信息熵对各种组合进行判定,如表2所示。
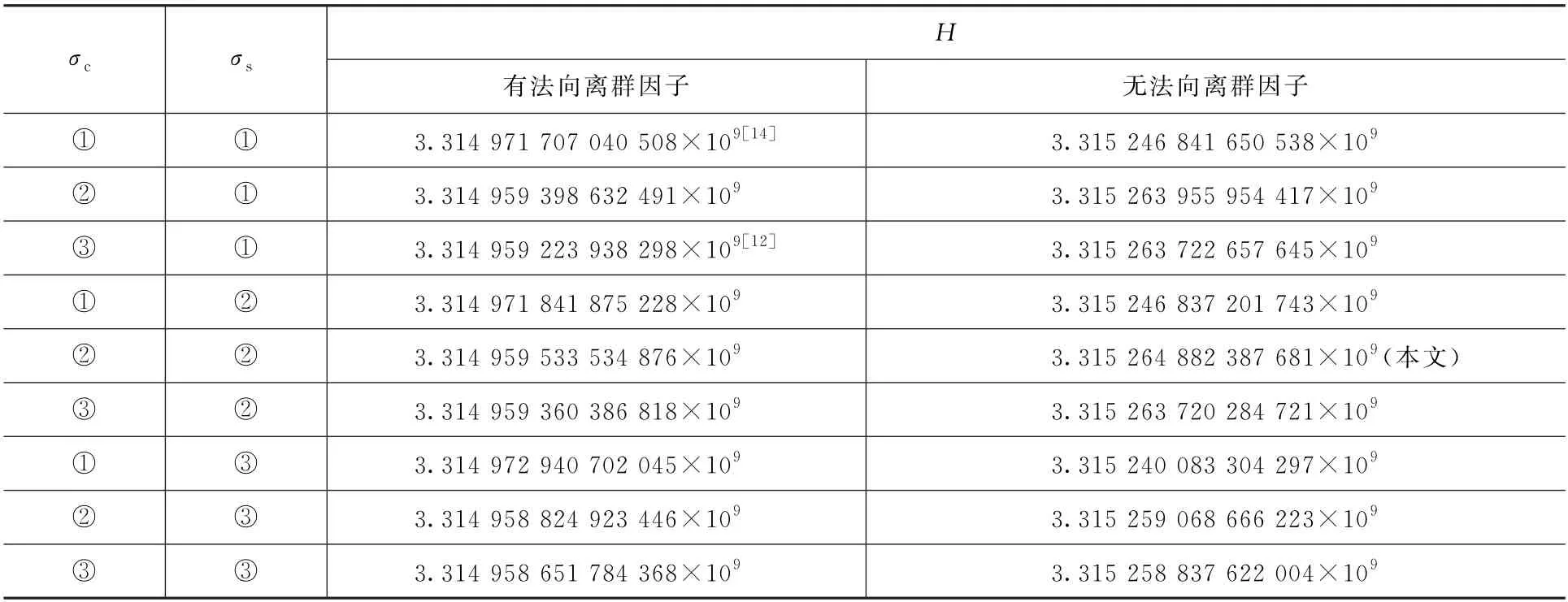
表2 各种组合下的全局信息熵
由表2可知,相比于文献[12]、文献[14]以及其他排列组合,本文算法的熵更大,保留的目标特征信息更多。
2.2 定量与定性评估
现有的滤波质量评价方法大多采用去噪前后点云数量的比值以及误差率作为评价参数。但是这种方法无法评估本身就带有噪声的源数据,因为其无法确定去除的点是否为噪声点,也无法判定目标细节特征的保留程度。
文献[14]提出了一种基于隐式移动最小二乘(implicit moving least squares,IMLS)的评估方法,利用当前点pi的邻域点构建隐式曲面,通过计算当前点到曲面的加权距离的平均值,即评估分数SIMLS,来评估滤波算法对细节特征的保留程度。细节特征保留程度越高,则评估分数SIMLS越低。SIMLS的计算公式为
其中
式中:Nf为经过滤波后的点云数据总量;dIMLS(i)为利用当前点与邻域点之间的空间距离及其在邻域点法线方向上的投影共同得到的加权距离;κ为法向离群因子。
采用传统双边滤波算法及本文算法对兔子模型进行滤波,滤波效果比较如图3所示。可以看出,无论是兔子的五官、背上的花纹,还是脚趾的形状,采用本文算法滤波后兔子模型能被清晰地刻画出来,滤波效果明显优于传统双边滤波算法。

图3 传统双边滤波算法与本文算法滤波效果比较
采用IMLS评估方法对不同滤波算法的性能进行评价,结果如表3所示。可以看出,文献[15]提到的半径滤波算法对目标细节特征的保留程度最差,而且耗时最长。除此之外,使用半径滤波算法需要不断调整参数以达到最优效果,人为因素干扰过多。与双边滤波算法相比,本文算法时间复杂度略高,但是保留了更多的目标细节特征。上述分析证明本文算法能够应用到实际点云处理中,实现有效滤波。
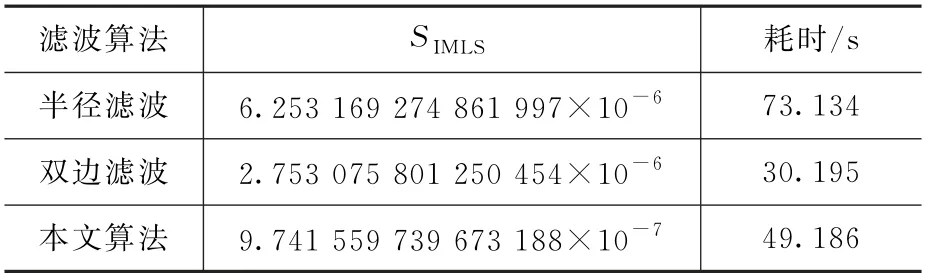
表3 不同滤波算法性能评估表
3 结论
针对现有点云滤波算法目标特征保留程度不高以及人为参与因素过多的问题,本文提出一种基于法矢量修正和参数修正的点云双边滤波改进算法。利用熵对所有空间距离权重因子与特征保持因子的组合进行评估,选出性能最佳的组合作为高斯核函数的参数,降低主观因素影响。利用滤波效果图和IMLS评估方法分别定性和定量地比较双边滤波改进前后的滤波效果。实验结果证明,本文算法能够详细刻画目标特征。算法的有效性得到了验证。
