融合深度学习与注意力机制的信道建模方法

张伟

（中国联合网络通信集团有限公司广东省分公司，广东 广州 510627）

0 引言

高铁高速运动等复杂通信环境受到多普勒频移和多径效应的影响，从而难以有效实现信道建模，信道建模不准确就会影响后续信道调解。虽然有学者提出数据导频辅助的信道估计方法[1-4]，其在一定程度上缓解导频不足和导频污染问题，但无法有效解决由于噪音和信道时变所带来的误差累积问题。也有学者采用深度学习[5-7]和多层感知机[8-9]来实现信道估计模型构建，但该方法没有考虑相邻OFDM 符号之间信道估计值可信度问题，从而没有对信道估计模型更新进行一个动态判决。因此，本文提出融合深度学习与注意力机制信道建模方法，该方法拟解决以下问题：（1）在发射机、接收机和障碍物随机移动通信场景，寻找一种可以根据环境变化对信道时域特征和频域特征进行有机融合的方法，并根据业务场景变化规律来强化或者弱化某些关键特征，从而有效解决时变信道误差补偿问题，有效应对动态通信环境中出现的多普勒频移和多径效应现象；（2）对通信环境小范围动态变化场景，寻找一种自适应调整采样间隔机制来降低整个系统的能耗，在一定程度上实现网络自感知、自决策。

1 融合深度学习与信道均衡的自适应采样间隔信道估计

1.1 建模思路

首先，在设定导频子载波采样间隔基础上，采用长短期记忆网络（Long Short-Term Memory，LSTM）+卷积神经网络（Convolution Neural Network，CNN）+数据导频辅助方法（Data Pilot Assistance，DPA）获得采样时隙OFDM（Orthogonal Frequency Division Multiplexing，正交频分复用技术）符号的信道频率响应值；然后采用信道均衡判断相邻采样时隙之间信道频率响应估计值的相似度，基于相似度来动态调整采样间隔；最后，将符合条件的信道频率响应值进行加权融合，实现信道频率响应值的重构，并将重构值作为下一帧的信号估计参数，实现信号调解。一帧具有M 个时隙信号，从M 个选择若干个时隙信号进行14 个OFDM 符号信号估计值后，将获得可信OFDM 符号进行重构后得到信道估计参数作为整一帧的信道估计参数用于信道估计。信道估计流程如图1 所示。

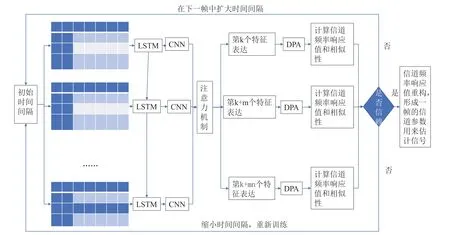
图1 信道估计流程

1.2 信道估计建模过程

（1）信号采集与信号表示

众所周知，一帧信号包含M 个时隙的信号（其中M与时隙的划分有关），为了准确估计下一帧的信号，通常需要抽取上一帧若干时隙的信号来估计信号估计参数。由于无线信号传播复杂性和随机性，在不同场景所抽取的时隙信号具有一定的时变性，为了更有效获取信号信息，通常对每一个时隙的信道数据进行固定间隔采样，结合导频子载波的信息来估计下一帧的信道估计参数。

假设OFDM 有效符号时间长度为Ts，加入循环前缀长度为Tg，那么OFDM 符号时间长度为T，表示为：

在某一个时隙中，对接收信号和发送信号均以Ts/N进行固定间隔获取采样数据点。在本文中，Tg取值为16 μs（每一个CP（循环前缀）时间长度是8 μs，一共有2 个CP，Ts取值为112 μs 每一个OFDM 有效符号时间长度是8 μs，一共有14 个OFDM 有效符号），为了简化表示，本文的对每一个时隙进行信息采样。信息采样过程如图2 所示。

图2 某一个时隙采样信息过程

通过对信息进行采样后，获得n个样本，每个样本都有64 行，分别包含64 个子载波的数据。将上述的n个样本输入到LSTM 中，获得抽样信息的时域关联语义。LSTM 处理采样信息的过程如图3 所示。

图3 基于LSTM获取信号的时域关联语义

设LSTM 的隐含层单元数量为m，经过LSTM 处理后，隐含层输出n×m维特征向量：

除了获取抽样信号的时域关联语义外，还需要获取抽样信号的频域关联语义，为了更加有效提取各个子载波的频域关联语义，将LSTM 获得的n×m个样本输入到CNN 网络，具体的处理过程如图4 所示。

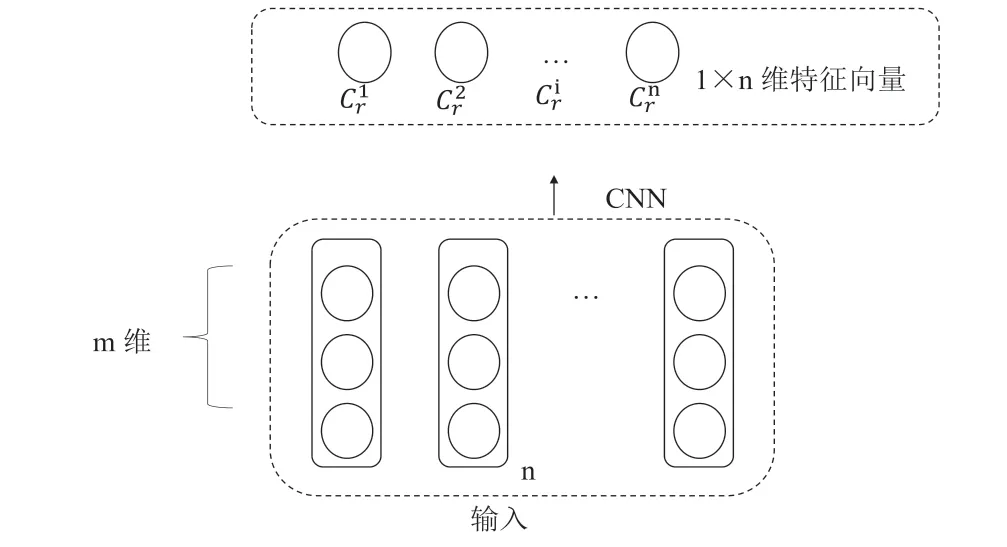
图4 基于CNN获取信号的频域关联语义

经过CNN 多个卷基层处理后，由n个神经元得到1×n维的特征向量：

（2）引入注意力机制实现信号时域关联语义和频域关联语义的有机融合

考虑到无线信号容易受到外部动态多变环境的影响，引入注意力机制根据不同时刻环境变化来实时更新时域和频域的关联语义，也就利用注意力系数Ci实现时域和频域关联语义的有机融合，更加有效表达信号的特征。注意力系数Ci表示为：

其中，exp()是一个指数函数。

结合注意力系数得到第k个时隙的特征表达。假设注意力系数的特征向量为C，注意力系数实质上就是对不同抽样时域输入向量进行有区别的赋值，结合LSTM 隐含层变量得到第k个时隙信号的时-空语义信息：

fk是第k个时隙信号的时-空语义信息，维度为1×n。

引入注意力机制将CNN 频域关联语义与LSTM 时域关联语义进行融合，使时间维度特征在某些数据维度加强，在某些数据维度减弱。因此，注意力机制能够很好应对信号受到某些因素影响呈现时强时弱的现象，从而有效应对复杂通信环境中出现的多普勒频移和多径效应的现象。

（3）基于信赖度的信道频率响应值重构方法

由于各个时隙计算的信道频率响应值是有差异的，因此，本文需要对比抽样时隙的信道频率响应值来计算信赖度，并将满足信赖度条件的信道频率响应值进行重构，以获得信道频率响应值重构值。

假设yk表示第k个时隙收到的信号值，结合第k个时隙的信号语义fk，第k个时信道频率响应值表示为：

hk表示第k个时信道频率响应值为了确保每一帧的信道频率响应值具有足够可靠性，本文对每一个抽样时隙所获得的信道频率响应值进行可信度评估，采样相似性来衡量抽样时隙所计算的信道频率响应值的信赖度，计算公式为：

对上述抽样时隙获得的信道频率响应值进行相似性判断，如果相似度满足信赖度阈值，则纳入信道频率响应值对应的数据库中，否则剔除。

将满足条件的信道频率响应值进行加权平均，实现信道频率响应值的重构。假设m+1 个时隙的信道频率响应值都满足要求，则将各个时隙的信道频率响应值加权平均，公式如下：

（4）基于估计误差的采样时间间隔动态调整

基于第T帧信号的导频子载波估计值为ZT，结合第T 帧信号的导频子载波真实值，得到T帧信号估计值的误差：

判断误差是否大于设定的误差阈值，如果大于阈值，那么缩小时隙采样间隔，相反，则扩大时隙采样间隔。其中间隔调整公式为：

一旦采样时间间隔发生变动，信道频率响应值将会改变，对应的处理单元所消耗的能量将会改变。

2 仿真分析

为了更加有效比较高速场景下的无线传输模型，考虑MIMO-OFDM 系统，仿真参数如表1 所示。

表1 仿真参数设置

根据参考文献[10]，城市主干道、高速公路和乡村道路三种场景下的均方差时延扩展和多普勒扩展数据展示如表2。

表2 三种场景下的信道参数测量值

由上面的信道参数可知，基于最大均方差时延扩展得到相干带宽约为455 kHz。

同样，最大的多普勒扩展得到的相干时间为：

该处仿真用的每一个OFDM 有效符号时间长度是8 μs，一共有16 个OFDM 有效符号。子载波为150 kHz，有效符号时间8 μs 远远小于相干时间227 μs，因此该信号传输的信道为慢衰落信道。这种慢衰落信道可认为是广义平稳信道，信道具有时变性。为了更有效估计信道参数，在仿真过程中将本文的算法与传统的最小二乘法(Least Squares Method,LS)算法所得到模型的误差和计算复杂度进行对比。

LS 算法具体的信道估计过程为：（1）首先基于数据导频的方法利用导频数据来估计信道的初始值，得到多个OFDM 符号的信道估计值；（2）采用逼零均衡算法（Zero-forcing，ZF）对多个OFDM 符号的信道估计值进行信道均衡，对导频数据的OFDM 符号的信道估计值进行修正；（3）在获取导频数据的OFDM 符号的信道估计修正值和信号实际接收值的基础上，采用LS 估计信道频率响应，将其用于下一个帧的信道估计。

本文算法的信道估计过程已经在上一节进行详细阐述，不再赘述。

（1）信道估计的MSE

为了对比不同方法在不同OFDM 符号训练样本数量下的MSE 值，首先是在设定导频数量和训练信噪比固定情况下，随着训练样本增加，其MSE 在三种场景的变化情况（注：按照2 μs 的固定时间间隔抽样，最多的抽样点为64×32=2 048 个）。

很明显，在“ 逐信噪比训练”下，LS 算法在噪音较大或者样本量较小时，其产生的误差比较大。图5 最上面3 条折线是样本量在100 时，随着信噪比不断增加，信道预测性能并没有得到很好的改善。当样本量增加到1 000 时，随着信噪比不断增加，信道预测性能不断改善，逼近0.005。当样本量增加到2 000 时，随着信噪比不断增加，三种场景的信道预测性能差距逐渐减小。

如图6 所示，采用本文的算法在“逐信噪比训练”下，在噪音较大或者样本量较小时，其产生的误差波动性相对于LS 算法来说平稳很多。虽然样本数量相同时，在低信噪比情况下，信道环境较差时两种算法的精度都不算高，差异不是太明显，但是本文算法的MSE 明显更加平缓，这是因为在信道条件较差时，线性估计的误差容易随着迭代的推进不断传递，最后导致信道估计容易失真。在高速移动场景下，LS 更容易受到多普勒频移的影响，其预测精度进一步受到影响。随着样本数量和信道环境的改善，本文算法在高速移动环境以及低速移动场景中都得到改善，差异逐渐减少，这是因为该算法引入注意力机制将CNN 频域特征表达与LSTM 时域特征进行融合，利用下一刻相邻OFDM 符号之间信道估计值的误差值来评估上一时隙的信道估计参数的精度，从而实现信道估计参数的自动校正。

图6 三种场景采用本文算法在不同样本数量下的信道估计MSE（训练信噪比为20 dB）

（2）信道估计的计算复杂度分析

为了对比不同方法在不同子载波数量下的复杂度，对比在设定导频数量情况下，随着导频数量增加，其在固定采样时间间隔、不同场景自适应采样间隔下的计算复杂度大小。具体如图7 所示。

图7 不同场景、不同算法的计算复杂度对比情况

图7 反映了不同场景不同算法在不同子载波的复杂度对比。仿真中，虽然LS 算法的计算复杂度较小，但是其信道估计精度是最差的。而乡道场景在自适应时间间隔的计算复杂度是最小的，这是因为乡道信道估计误差的变化较小的情况下会调大采样时间间隔，从而信道估计算法在时间上小范围波动情况下大大降低了计算复杂度，从而降低网络资源的能耗。

3 结束语

本文在信道估计算法基础上，重点研究5G 在高速移动场景下精度高、自适应更新采样间隔的时变信道建模算法。在信道建模过程中，利用深度学习的非线性拟合能力、鲁棒性强的特点，引入注意力机制实现信号频域特征和时域特征的有机融合，从而有效应对复杂通信环境中出现的多普勒频移和多径效应的现象。除此之外，本文采用自适应采样间隔来动态调整信号采样间隔，解决信道小范围波动所导致计算资源浪费问题，降低了网络的能耗。仿真可知，该方法能够为后续的自感知、自决策网络建设提供方法参考。