城市道路车辆行为识别方法研究*

陆金辉，鲍楠，胡晗，左加阔，师晓晔，潘甦

（南京邮电大学，江苏 南京 210003）

0 引言

分析和识别车辆的各种行为是智慧交通系统发展中必须研究和解决的重要任务。根据国家统计局数据，2021 年全国共发生道路交通事故273 098 起，其中涉及车辆变道的事故共7 370 起，占比2.7%[1]。驾驶员操作不规范、存在视线盲区、车辆间安全距离不足等都有可能造成事故的发生，因此需要驾驶员能够准确判断目标车辆的行为，例如左转或换道等。如果主车辆能够及时识别目标车辆的危险动作，则可以避免严重事故。

近年来，车辆行为识别得到了广泛地关注。准确识别或预测目标车辆行为有助于提高道路交通安全性，降低事故发生率，为此国内外学者做了大量的研究。文献[2] 提出了一种基于卷积神经网络(Convolutional Neural Networks,CNN) 的驾驶人行为识别方法，通过多层卷积和全连接层完成对车辆行为的分类。文献[3] 利用隐马尔科夫模型(Hidden Markov Model，HMM) 的时序性和支持向量机(Support Vector Machine,SVM) 的分类特性以达到提高准确率的效果，提出了一种基于HMM 和SVM级联算法的车辆驾驶行为识别方法。文献[4] 比较分析了不同变道策略下的变道时间以及方向盘角度、相对距离和相对速度等特征参数，采用随机森林（Random Forest,RF）分类器来构建车辆行为识别模型。文献[5]提出了一种基于长短时记忆神经网络（Long Short-Term Memory,LSTM）的车辆行为识别方法，通过引入注意力机制，利用网络中自学习过程产生的权重，对LSTM 在不同时间的输出结果进行了权重求和，以便于有效使用编码信息从而提高对车辆变道行为的辨识性能。文献[6] 提出了一种基于SVM 的变道车辆轨迹预测方法，利用当前驾驶员在变道过程中的行为和车辆的完整轨迹，结合SVM 识别纵向和横向的预测误差。文献[7] 将K 邻近分类算法（K-NearestNeighbor，KNN）引入异常激进驾驶预警系统以帮助诊断识别驾驶员不规则车辆行为。文献[8] 利用LSTM 可以捕获和建模时间序列数据中的长期相关性的性质，以推断接近十字路口的车辆的驾驶意图。文献[9] 用语义定义的车辆行为适应各种驾驶场景，并结合神经网络（Neural Network，NN）对周围车辆的运动状态信息进行估计以推断车辆行为。

由此可见传统的道路车辆行为识别方法主要是基于机器学习算法，例如SVM、KNN、RF、LSTM 和HMM 等。然而上述方法通常需要手动选择特征，过程繁琐，自适应较差。此外，传统的行为识别方法还面临难以处理时序数据、模型复杂度过高等问题。因此，本文提出一种基于混合高斯隐马尔科夫模型（Mixed Gaussian Hidden Markov model,GM-HMM）的城市道路车辆行为识别方法，通过使用高斯混合模型（Gaussian Mixture Model,GMM）对特征数据进行建模，同时使用HMM 对整个车辆行为序列进行建模。与传统方法相比，这种方法无需手动选择特征，具有自适应性和对时序数据的优秀处理能力。此外，该方法具有较高的准确性和鲁棒性，能够有效地应用于实际道路交通场景中，预防交通事故的发生。本文的创新点在于将GM-HMM 与城市道路车辆行为识别相结合，并通过仿真实验验证了该方法的有效性。

1 数据采集和处理

本文通过仿真平台模拟城市道路交通场景，获取了城市三车道道路车辆行驶场景的车辆运动数据。在仿真过程中，需建立仿真基础场景，包括车辆、道路和交通设备等，提供仿真交通控制模块，包括周围车辆的运行状态等[10]。研究对象为典型的城市三车道道路车辆行为，行驶场景如图1 所示，目标车辆与主车行驶在同一车道，车辆1、车辆2、车辆3、车辆4 是周围参考车辆，分布在中间车道的两边。在该场景中，目标车辆可以直行或左换道，为保证主车的驾驶安全性和舒适性，需要预测识别目标车辆的行为，本文主要识别的是目标车辆直行，左换道，右换道三种行为。

图1 城市三车道道路车辆行驶场景图

换道是驾驶员根据具体交通场景需要改善行车环境或节省时间，将车辆从一个车道移动到另一个的过程的操作。一般换道过程中，车辆的变化可以描述成如下几个阶段：

（1）初始阶段：在换道开始时，车辆通常保持正常行驶速度，并开始观察适当的时机和间隙来进行换道。

（2）加速阶段：一旦驾驶员决定进行换道，车辆将开始加速以到达目标车道，加速过程中，车辆逐渐增加速度，直到达到目标位置，同时驾驶员需要确保本车辆与其他车辆保持安全的距离。

（3）恒速行驶阶段：恒速行驶阶段是车辆换道过程中速度保持稳定的阶段，一旦车辆行驶至目标位置，它将保持恒定的速度，从而维持与周围车辆的安全距离。

（4）减速阶段：在车辆到达目标车道一段时间后，需要减速到原来正常行驶速度并注意后方车辆的反应和响应时间。减速阶段中，车辆速度逐渐减小，直到与初始阶段速度相同。

在特征参数选择上，其需要具有良好的区分度并且能够有效地反映目标车辆的行为，以提高识别的准确度。但是过多的特征参数反而会极大地增加计算量，为了在车辆行为识别过程中减少计算复杂度，应选择较少的并具有代表性的特征参数以提高算法的效率[11]。在目标车辆进行车道变换时，它的纵向速度Vx、横向速度Vy以及其车头中心与初始时刻所在车道右侧车道线的距离dr这3 个可测量信号相对于直行时会发生对应的明显变化。因此，将Vx、Vy和dr作为识别目标车辆行为的特征参数。

为了训练HMM 模型的参数，往往需要充分的数据支持。本文通过使用仿真平台模拟城市道路场景下的车辆行驶状态，以实现车辆行为的识别。考虑到车辆行为的连续性，每秒内进行了10 次数据采集，以获取目标车辆的Vx、Vy和dr等特征参数形成观测序列。总计记录了390 组目标车辆的行驶状态参数数据。这些数据被分为两个部分，其中一部分用于模型的训练，分析目标车辆在不同车辆行为下特征参数的变化规律，并训练相应的车辆行为识别模型；其余的数据用于模型测试，来评估所建立的车辆行为识别模型的准确率。

2 混合高斯隐马尔科夫模型

2.1 HMM基本理论

HMM 是一种统计模型，可以用于建模时间序列数据。它假设观测数据是由一系列未知的状态序列生成的，并通过状态转移和观测概率矩阵来对观测数据进行建模和识别，可以将序列的每个位置看作一个时刻[12]。状态序列中每个状态都是隐藏的，即不可观测到的，故被称为隐状态，例如车辆行为识别中的左换道，右换道，直行等状态，它们对于传感器来说是无法直接观测到的。观测序列是可观测的数据序列，它们是根据相应的状态序列生成的，例如车辆行为识别中传感器能够直接采集到的位移、速度等车辆数据。HMM 对观测事件的概率建模基于两个假设：(1) 齐次马尔科夫假设：t时刻隐状态仅受t-1 时刻的状态影响；(2) 观测独立性假设：任何时刻的观测仅依赖于当前时刻的状态[13]。

通常情况下，一个HMM 模型可由以下参数进行描述：λ＝{E,F,A,B,π}，π和A决定状态序列、B决定观测序列，通常简记为λ＝{A,B,π}，各参数意义如表1 所示。

表1 HMM参数表

HMM 每个时间步都存在着两组相应的变量。如图2所示，其中上面的是隐状态变量，其会随时间按一定概率变化，下面的是观测状态变量，其可以是离散或连续的且只取决于当前时刻隐状态变量。St表示系统在t时刻的状态，其对应状态可表示为St=qi，其取值集合记为S。Ot表示系统在t时刻的观测，其对应观测值可表示为Ot=vk，其取值集合记为O[14]。

图2 HMM结构示意图

已知HMM 模型λ，观测序列长度为T，S={S1,S2,…,ST}是长度为T的状态序列，O={O1,O2,…,OT} 是对应的观测序列，则观测序列O的生成过程可以描述如下：

（1）初始状态设置：由初始状态分布π产生状态S1=qi，其中qi是隐状态的取值之一；

（2）时间步t的设置：令t=1；

（3）观测生成：根据状态St=qi的观测概率分布bi(k) 生成Ot=vk；

（4）状态转移：根据状态St的状态转移概率分布aij产生下一个状态St+1=qj；

（5）更新时间步：令t=t+1，如果t＜T，转到（3）；否则终止生成并输出O。

2.2 GM-HMM模型构建

高斯混合模型（GMM）能够无限逼近任意连续型变量的分布，考虑到车辆的机动行为通常被视为连续、时变和动态过程，故车辆运行数据为连续型变量，因此采用GMM 建立状态输出事件的随机分布函数[10]。GMHMM 模型参数可用一个五元组表示：λ＝{π,A,c,μ,G}，其中π为初始状态概率向量；A为状态转移矩阵；c为高斯分量权重系数；μ为高斯均值矩阵；G为高斯协方差矩阵。对于一个GM-HMM 模型，与HMM 相比而言，每一个隐状态所对应的观测值由多个多维高斯函数生成，输出的观测值B经由GMM 拟合并且不再是一个混淆矩阵，而是一组观测变量的连续概率密度函数，可以表示为：

其中，F表示隐状态j包含的高斯混合数，Cjf表示隐状态j下第f个混合高斯元的权重，Cjf≥0，权重之和为1，μjf表示隐状态j下第f个混合高斯元的均值矩阵，Gjf表示隐状态j下第f个混合高斯元的协方差矩阵，N表示多维高斯概率密度函数[15]。

多维高斯概率密度函数N表达如下：

2.3 参数训练

HMM 主要涉及3 大问题，分别为隐状态概率计算、参数学习和隐状态过程求解问题。在车辆行为识别领域中，一般使用前后向(Forward-backward) 算法来实现对已收集到的车辆观测数据进行隐状态概率计算，根据鲍姆-韦尔奇(Baum-Welch) 算法来进行参数学习[16]。

在本文中车辆行为被分为3 类，即直行、左换道和右换道。GM-HMM 的参数学习也称为参数训练，即给定观测序列O＝{O1,O2,...,OT}，学习模型参数λ＝{π,A,c,μ,G}，需要训练参数，使得在该参数下，观测序列概率P(O|λ)最大[17]。

GM-HMM 参数训练的过程如下：首先为每个车辆行为子模型设定初始参数，再从用于计算初始均值矩阵μ0和协方差矩阵G0的训练数据中选取一组样本数据并进行输入，根据前后向算法计算内部状态的前向和后向概率。其次计算每个观测值的中间辅助变量，根据鲍姆-韦尔奇算法迭代地更新模型参数，使其最大化训练数据样本的似然性。在每次迭代的过程中，依据当前参数计算前向概率、后向概率和辅助变量，并不断更新模型参数。重复执行该过程，直到模型参数收敛，最后保存并得到3 个车辆行为子模型的最终参数[18-19]。

一般情况下，参数π和A对最终训练结果的影响十分微小，故能够任意设置其初始值，因此，将π和A用式（3）和（4）进行初始化。然而，C，u和G的初始值对最终训练结果有显著影响，可以采用自动聚类算法对其进行初始化。

本文通过使用Python 中的编写程序来训练相应模型，以建立独立的HMM 来描述目标车辆的3 种车辆行为。

2.4 城市道路车辆行为识别

如图3 所示，将测试数据样本依次输入3 个子模型（直行GM-HMM、左换道GM-HMM、右换道GM-HMM）中，通过前后向算法分别计算3 个子模型产生该观测序列的概率P(O|λ) 并进行比较。如果某一个模型的输出概率值最大，则表示该子模型与给定观测数据的匹配度最高，其对应车辆行为即为待识别状态结果[20]。

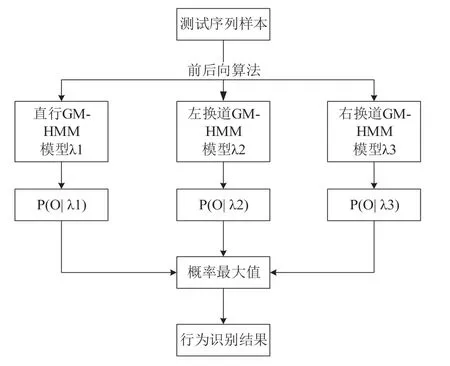
图3 城市道路车辆行为识别过程

为了解决数值下溢问题、简化计算和方便参数估计，提高HMM 中概率计算的效率和稳定性，本文对计算识别概率结果取对数，对应的3 个车辆行为模型计算部分样本结果如表2 所示。根据最大似然估计原理，需要选择能够使观测数据出现概率最大的模型作为最可能匹配的模型，故将每行最大数值对应的车辆行为作为识别结果，并标出识别正误。

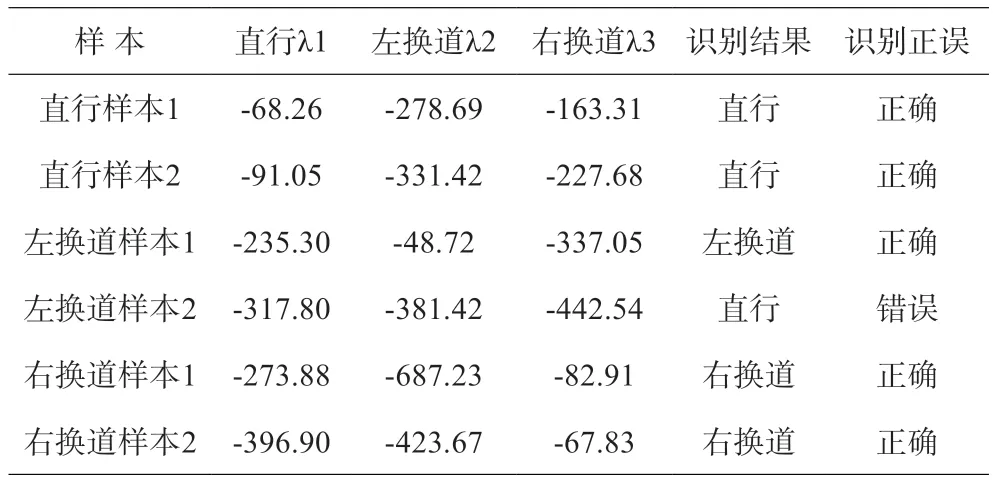
表2 车辆行为识别结果

3 实验结果分析

通过仿真平台构建城市三车道道路场景，在场景项目中以图1 的目标车辆左换道为例。添加目标车辆和周围参考车辆，将目标车辆放置在所需车道和位置上，确保目标车辆与主车行驶在同一车道，将车辆1、车辆2、车辆3 和车辆4 分布在其他车道，以模拟周围参考车辆的行驶。所有车辆按照预定义规则进行路径规划，并遵守交通规则。

目标车辆左换道场景具有以下属性：

（1）车辆1、车辆2、车辆3、车辆4 和主车均以V=15 m/s 匀速行驶，且与目标车辆保持一定的安全距离。

（2）设置每个车道宽均为3.6 m,车辆尺寸为所选择仿真车辆模块设定尺寸,每一路段距离为200 m。

（3）目标车辆起始以15 m/s 匀速行驶，其进行左换道时先加速至20 m/s，当穿越车道线到达目标位置后将保持恒定的速度行驶t0时间，从而维持与周围车辆的安全距离。经过t0后目标车辆减速至初速度15 m/s 后继续匀速行驶，并根据其位置坐标记录其车头中心与初始所在车道右侧车道线的距离。

（4）当目标车辆完成换道后，所有车辆均继续直行到路段终点，场景结束。

（5）完成之前的场景后，所有车辆行驶到新的路段，新场景立即重新启动，以确保驾驶场景之间的连续性。

（6）每次换道过程至少持续4 s，以确保完全改变车道或保持车道。

时间窗口大小的选取对于识别准确率具有重要影响，较短的时间窗口可能无法捕捉到足够的行为特征，导致识别准确性降低，而较长的时间窗口可能引入过多的上下文信息，并且需要更长的计算时间[21]。本文研究了不同时间窗口大小下的行为识别准确率，如图4 所示，包括0.5 s、1 s、1.5 s、2.0 s、2.5 s 和3.0 s。比较发现，在2.0 s 时间窗口下，对应的三种车辆行为的识别准确率最高，故2 s 的时间窗口大小能够在捕捉目标车辆行为细节的同时保持较高的识别准确性，为最优选择。因此本文使用2.0 s 的时间窗口进行连续识别，每次移动间隔设置为1.0 s，由此产生的每个观测序列长度为20，其中每个时间点都记录了目标车辆的特征参数值数据。

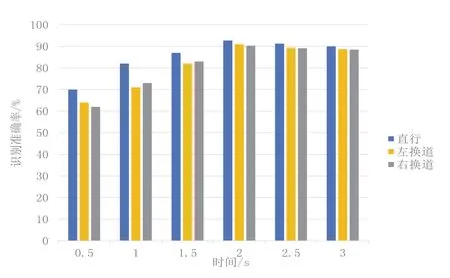
图4 不同时间窗口下的识别准确率

为检验所建立的车辆行为识别模型的效果，采用识别精度来评估模型识别任务中的性能。它反映了模型正确识别的样本在总样本中的比例。通过仿真平台收集的样本数据进行车辆行为识别精度检验，如表3 所示，在2.0s时间窗口大小下的样本检验中，150 个直行样本有139 个被准确识别，识别精度达到92.7%，120 个左换道样本有108 个被准确识别，识别精度达到90%，120 个右换道样本检验有109 个正确样本数，识别精度达到90.8%，表明预测模型的识别性能良好。

表3 车辆行为识别精度

同时，本文还对比了不同算法下对车辆行为识别的准确率，例如本文中的直行、左换道、右换道三种行为的混合，如表4 所示，包括SVM、K-NN、HMM 和GMHMM，通过分析车辆行驶特征数据来判断当前的行为。在车辆行为识别方面，SVM 达到了较高的准确率，为87.2%；由于KNN 的预测速度较慢，对异常值敏感等缺陷，KNN 准确率相对较低，为77.8%；HMM 的准确率为88%；GM-HMM 实现了最高的准确率，达到91.2%。

表4 不同算法下的车辆行为识别准确率

综上所述，相对于其他算法，GM-HMM 结合了HMM 和GMM 的优势，能够更准确地对车辆行为进行建模和识别，提高了准确率。由此可见，本文提出的GMHMM 算法在车辆行为识别领域具有较高的精度和鲁棒性。

4 结束语

根据对GM-HMM 的应用和仿真结果的分析，本文成功地提出了一种基于该模型的车辆行为识别方法。通过仿真获取城市道路场景下车辆运动轨迹信息和车辆信息，并对这些信息进行了数据处理和特征参数选取。通过对模型参数进行训练迭代更新，结合前后向算法，成功实现了对城市道路车辆行为的准确识别。实验结果表明，相较于其他算法，采用GM-HMM 进行车辆行为识别具有较高的精度。该方法的应用可以帮助提高城市道路驾驶的安全性，为交通管理和智能交通系统等领域提供重要的数据支持，具有重要的实际应用价值，并为进一步研究和发展交通安全和智能交通技术提供了有益的借鉴和启示。

然而，该方法仍然存在一些挑战和改进的空间。例如，模型的训练和更新过程可能受到数据噪声和异常值的影响。此外，对于复杂的交通场景或特定的车辆行为，模型的性能可能会有所下降，需要进一步优化和改进算法以应对更多的驾驶情况。