考虑不确定性多智能体系统的分布式容错控制

王艳丽, 孙利娟

(1. 河南科技大学 软件学院, 河南 洛阳 471003; 2. 开封文化艺术职业学院 计算机学院, 河南 开封 475000)

多智能体系统中的每个单体都有相对独立的行为能力,通过信息交互实现类似于生物体的群集活动,多智能体系统是目前研究的热点之一[1-2],广泛应用于无人机编队[3]、机器人编队[4]、卫星编队和智能交通[5]等领域.在建立智能体模型时,往往会出现未建模动态,而且随着工作环境和条件的变化,智能体的系统参数也会发生摄动.另外,由于多智能体在工作时,通常处于长时和高频振动的状态中,增大执行器发生故障的概率.这些不确定性会对多智能体系统的一致性控制带来困难[6-7].

刘自理等[8]为解决多智能体系统的通信时延和数据丢失问题,引入队列机制设计了分布式输出反馈控制算法,实现了多智能体系统的协同工作;刘秀华等[9]设计了一种分布式观测器,其可以准确地估计出多智能体系统状态和执行器故障,但是该方法没有涉及容错控制;曹伟等[10]设计了基于离散时间迭代学习的控制方法,但是该算法的收敛条件比较严格;刘凡等[11]利用干扰观测器估算出智能体的状态,实现了多智能体系统的一致鲁棒控制.通过以上分析可发现,针对包含有未建模动态和参数摄动不确定性以及执行器故障的多智能体系统的研究成果较少.因此,本文针对不确定条件下的多智能体系统,在领导者和领域内智能体状态量的基础上,设计了包含参数自适应律的分布式容错控制方法.

1 多智能体系统模型

首先将多智能体系统之间的通信和队形拓扑关系通过有向图表示[12],然后假设系统包括1个领导者和N个跟随者,并分别用M0和M1,M2,…,MN来表示,M0的状态描述为

(1)

(2)

式中:xi(t)为Mi的状态量;ui(t)为Mi的控制输入;ΔAi(xi(t),t)为Mi的未建模动态和参数摄动等不确定性总和,这种不确定性是与系统状态相关的[13],满足条件

(3)

式中:θ1i,θ2i>0为未知变量;α为范数值.

智能体在长时间、高频率、高强度的工作状态下,执行器容易发生失效乘性故障和偏离加性故障,故障模型可描述为

ui(t)=[I+ΔKi(t)]vi(t)+dKi(t)

(4)

式中:ΔKi(t)=diag[δkij]n×n为失效乘性故障;dKi(t)=[dki1,…,dkij,…,dkin]T为偏离加性故障.包含不确定性和执行器故障的模型描述为

[I+ΔKi(t)]vi(t)+dKi(t)

(5)

定义跟踪误差ei(t)=xi(t)-x0(t),则误差微分方程为

[I+ΔKi(t)]vi(t)-v0(t)

(6)

2 容错控制律设计

采用参数自适应技术设计分布式容错控制律,其表达式为

(7)

式中:aij为Mi与Mj的通信链接状态;g(ei)=[sgn(ei1),sgn(ei2),…,sgn(ein)],eik为ei的第k个元素;Ki(t)可表示为

(8)

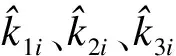
[ei(t)-ej(t)]-βΔig(ei)Ki+hi(t)

(9)

式中:βΔi=I+ΔKi;hi(t)=ΔAi(xi(t),t)x0(t)-v0(t)+dKi(t).由于x0(t)、v0(t)和dKi(t)均有界,则根据式(3)得到

(10)

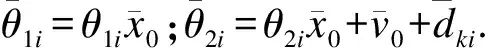
βΔg(e)K(t)+h(t)

(11)

3 稳定性分析

定理1:针对带有不确定性和执行器故障的多智能体系统,设计包含增益和自适应律的分布式容错控制律,能够确保一致性误差收敛到零.

证明:构建Lyapunov函数[14]为

(12)

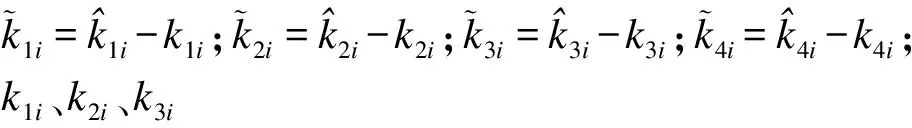
(13)

(14)

由矩阵L的表达式可得到矩阵L的每一行、列的和都为0,则可得到

eTLe≤0

(15)

将式(3)、式(15)代入式(14)中,可化简得到

(16)

由于式(16)中的参数都是有界的,则可以定义

(17)

进一步可得

(18)

根据Lyapunov稳定性定理可知定理1成立.即包含增益和自适应律的分布式容错控制律能确保多智能体系统的一致性误差收敛到零.

4 实验结果与验证分析

为了验证考虑不确定性多智能体容错控制方法的优越性,对无人机编队模型进行Matlab/Simulink仿真验证,无人机动力学模型表示为

(19)

式中,xi(t)=[vi(t),φi(t)]T为表征第i个无人机的速度和航迹角的向量,并可作为多智能体系统的一致性变量进行仿真.

4.1 实验参数设置

实验中,选取4架无人机组成多智能体系统,分别记为M0、M1、M2和M3,包含有向生成树的拓扑结构如图1所示,其中,通信链接a13=a31=1,而a12=a21=a23=a32=0.

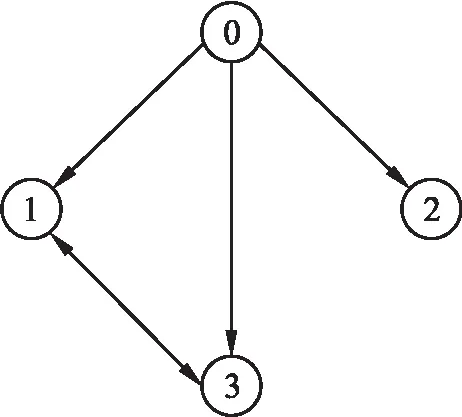
图1 多智能体拓扑结构Fig.1 Multi-agent topology

选取容错控制律中的参数ri=6、li=8、si=4、wi=12.初始状态设置为[v0(0),v1(0),v2(0),v3(0)]=[30 cm/s,15 cm/s,35 cm/s,40 cm/s],[φ0(0),φ1(0),φ2(0),φ3(0)]=[20°,6°,28°,35°].

设置速度指令和航迹角指令分别为30 cm/s和20°,整个仿真时间为10 s,期间持续存在不确定性ΔAi.当t=5 s时,执行器发生失效乘性故障ΔKi和偏离加性故障dKi,分别设置ΔAi、ΔKi和dKi为

(20)

4.2 速度和误差跟踪与对比

文献[15]利用神经网络来估计未知非线性执行器故障,并与动态面技术相结合,提出了一种自适应协同容错控制方法.为了验证本文提出的容错控制律的优越性,将其与文献[15]进行对比,得到多智能体系统的速度跟踪曲线如图2所示,速度误差曲线如图3所示.

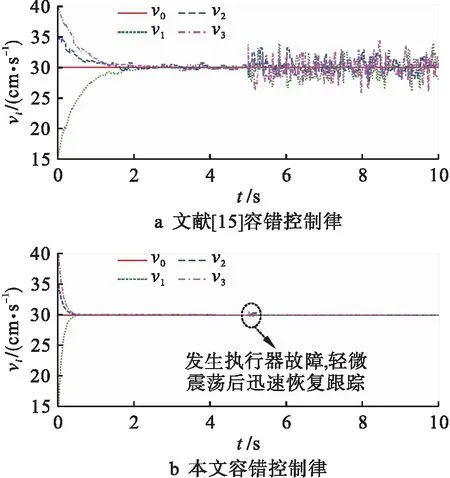
图2 速度仿真曲线Fig.2 speed simulation curves

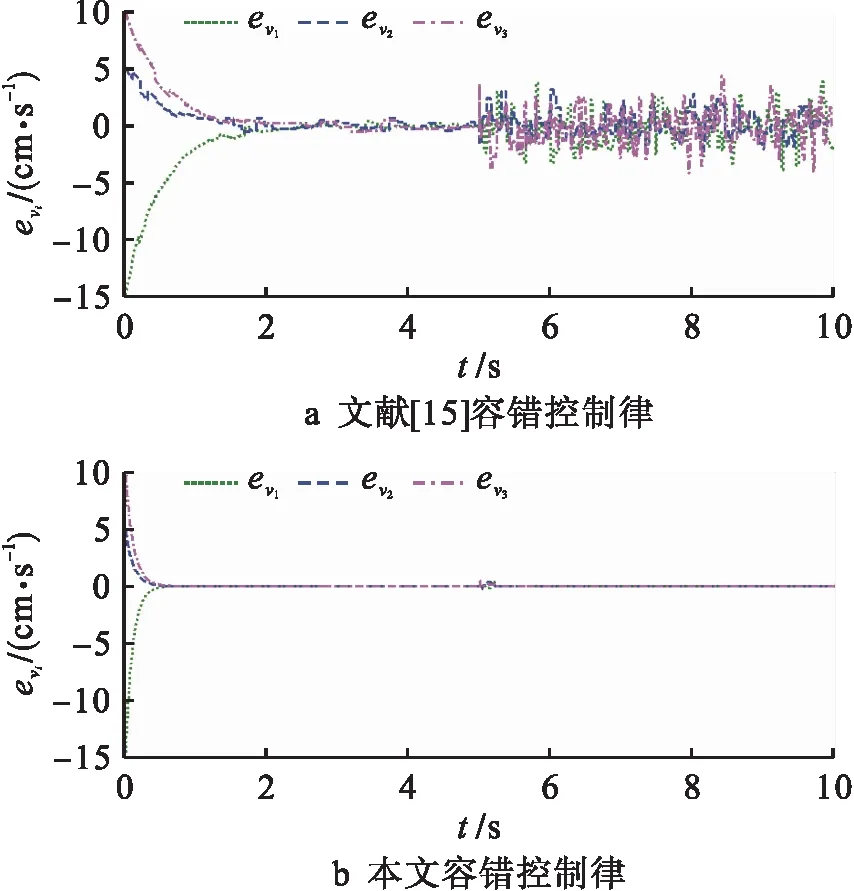
图3 速度误差仿真曲线Fig.3 Speed error simulation curves

从图2结果可以看出:在文献[15]控制方法作用下,M1、M2和M3虽然在2 s后能够大致跟踪指令信号,但是响应时间比较长,同时跟踪曲线发生剧烈振荡,当执行器出现故障时,跟踪曲线发生剧烈波动,控制效果较差;而在文本容错控制律的作用下,M1、M2和M3能克服不确定性的影响,在0.4 s时就可达到一致稳定,当执行器发生故障时,跟踪曲线发生微小振荡后,可迅速稳定跟踪速度指令信号,控制效果表现得更好.

从图3结果可以看出:在文献[15]容错控制律的作用下,速度误差持续小幅振荡,2 s后减小到0 cm/s附近,而在执行器故障的影响下,持续大幅振荡,控制效果不好;本文设计的控制律能确保M1、M2和M3的跟踪误差在0.5 s减小到0 cm/s,当故障发生时,跟踪误差小幅振荡后,在0.2 s内减小到0 cm/s.

4.3 航迹角和误差跟踪与对比

与4.2节中速度对比方法相同,得到多智能体系统的航迹角跟踪曲线如图4所示,航迹角误差曲线如图5所示.

图4 航迹角仿真曲线Fig.4 Track angle simulation curves

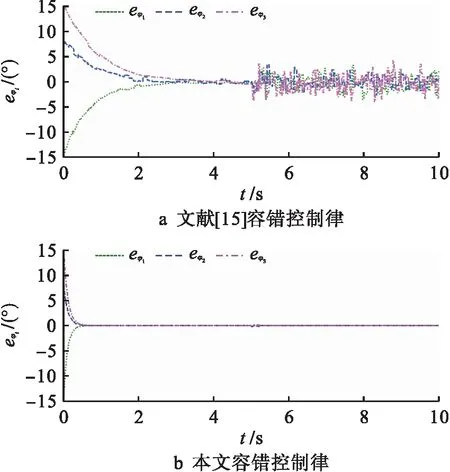
图5 航迹角误差仿真曲线Fig.5 Track angle error simulation curves

具体分析方法与图2、3相同,可看出本文容错控制律能够包容不确定性和执行器故障的影响,快速实现对多智能体系统的一致稳定,控制效果更优.

5 结 论

针对多智能体系统中参数摄动不确定性和执行器故障等问题,利用参数自适应技术设计了分布式容错控制律.通过在Matlab中对无人机编队进行仿真实验表明,所设计的容错控制律能够使多智能体在0.5 s内跟踪指令信号,能够包容未建模动态和参数摄动等不确定的影响,实现多智能体系统的一致鲁棒控制;可在0.5 s后使跟踪误差减小到0 cm/s,控制精度较高,也能够克服执行器失效乘性故障和偏离加性故障的影响,实现多智能体系统的一致容错控制.