基于动态KECA的工业过程故障检测

郭金玉, 朱明坤, 李 元

(沈阳化工大学 信息工程学院, 沈阳 110142)

近年来,随着科技的高速发展,各种新的计算机技术不断产生,针对传统的故障检测方法也提出了许多新的理论.在现代工业过程的生产运行中,工艺流程的复杂程度日益增加,产生的数据量变得十分庞大,其中也会掺杂许多难以预料的干扰,这对于工业过程的故障检测和诊断来说是一个非常大的挑战.通过对系统进行实时准确的故障检测,在早期发现和处理故障,避免事故发生,对于工业过程有着重要的实际意义.为了确保工业生产过程的可靠性和安全性,对于数据之间广泛存在的非线性和动态延迟等问题,已经提出了多种基于多元统计分析的技术方法[1-3].

主成分分析(principal component analysis,PCA)作为一种经典的故障检测方法被广泛应用,其能够保留线性系统的主要特征,通过数据降维对系统进行分析.陈杨[4]将PCA方法用于热连轧打滑过程的故障检测.在PCA方法的基础上,专家学者进行不断的优化和改进,提出许多新的应用.柯程扬等[5]将PCA与KNN方法相结合实现对金线莲种类的识别.史东海等[6]运用EMD和PCA方法对数据进行特征降维,实现滑动轴承的故障诊断.PCA方法通常只适用于变量服从多元高斯分布的系统,对于非线性系统的检测效果较差.为了应对系统存在的非线性问题,研究人员提出了核主成分分析(kernel principal component analysis,KPCA)方法.KPCA方法将数据通过核函数映射到特征空间,在高维空间上对数据进行处理.张志政等[7]将KPCA方法与粒子群优化、支持向量机方法相结合用于船舶燃油系统的故障监测与诊断.李学渊等[8]通过KPCA方法将系统划分为特征空间和残差空间,实现对环网柜的故障检测.在实际的工业过程中,系统存在的动态特性对于故障检测的影响非常大.针对系统间存在的动态特性,通过时滞位移将系统动态特性的概念引入到PCA方法中,提出动态主成分分析(dynamic principal component analysis,DPCA)方法,有效地解决了线性系统中的动态特性.RATO和刘鸿斌等[9-10]在此基础上将动态核主成分分析(dynamic kernel principal component analysis,DKPCA)方法应用于复杂污水处理过程的故障检测,可有效应对系统的动态特性.JENSSEN[11]将信息熵的概念引入KPCA方法中,提出核熵成分分析(kernel entropy component analysis,KECA)方法,在数据转换和维度降低时能够利用信息熵的定义更加充分地表达出数据中的信息.目前,KECA方法在故障诊断领域得到了广泛应用,并针对不同问题提出许多改进方法[12-14].但对于复杂的动态非线性工业过程,现有的静态KECA及其改进方法难以取得良好的检测结果.本文将时滞位移方式引入到KECA中,提出一种动态核熵成分分析(DKECA)方法,用于动态非线性系统的故障检测.

1 动态KECA方法基本原理

假设一个m维数据矩阵在k时刻时表示为xk=[x1(k),x2(k),…,xm(k)]T,引入时间延迟系数l,构成增广数据矩阵为

(1)

式中,n为样本数量.根据研究人员的经验,线性系统中l的取值通常为1或2,非线性系统则往往会更大一些.

对于一个由概率密度函数p(x)生成的数据集Dl={x1,x2,…,xn},其Rényi熵可定义为

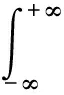
(2)

(3)

式中:kσ(x,xt)为Mercer核函数;σ为核函数的参数.通过样本均值的近似估计可得

(4)

式中:K为n×n的核矩阵;I为一个n×1的单位向量.Rényi熵的值可以通过核矩阵K的特征值和特征向量进行估计,将核矩阵K进行特征值分解得到K=ETΛE.其中,Λ为由核矩阵的特征值λ1,λ2,…,λn组成的对角矩阵,E为由特征值对应的特征向量e1,e2,…,en组成的矩阵.由式(4)可得

(5)

(6)

式(5)中的每一项都对熵的估计值做出贡献,这意味着熵的估计值不完全取决于特征值的大小,而是共同取决于特征值和特征向量.

将输入数据集通过非线性φ映射到核特征空间中,该空间中的数据集可表示为Φ=[φ(x1),φ(x2),…,φ(xn)].对Ψi大小进行降序排列,选取熵值贡献较大的前k个特征向量PUk,通过KECA产生转换后的数据为

(7)

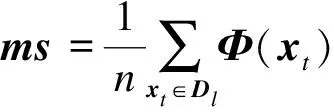
(8)

(9)

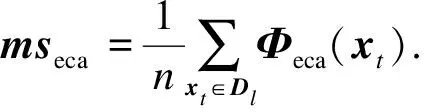
(10)

2 基于DKECA的故障检测方法

经过DKECA方法变换后,其角结构特性会体现在DKECA模型中,因此使用Cauchy-Schwarz(CS)统计量作为模型的监测指标.CS统计量是在Cauchy-Schwarz不等式基础上拓展出来的,计算两个概率密度函数p1(x)和p2(x)在某种意义上的接近或相关程度的统计量,其值大小位于0和1之间,表达式为

(11)

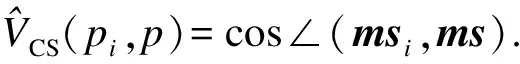
基于DKECA的故障检测过程分为两个阶段,分别是建立离线模型阶段和在线检测阶段.基于DKECA的故障检测流程图如图1所示.

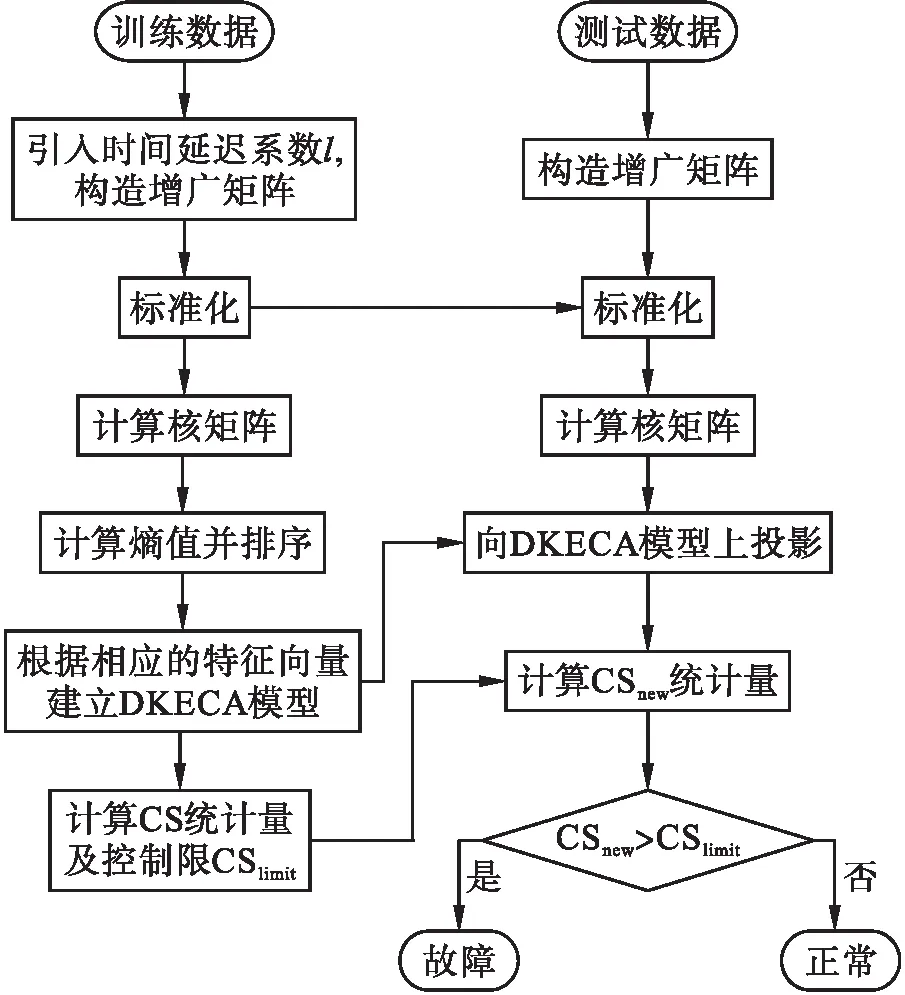
图1 基于DKECA的故障检测流程图Fig.1 Flow chart of fault detection based on DKECA

1) 建立离线模型的具体步骤如下:

① 选择合适的时间延迟系数l,构建增广矩阵Xl;

② 根据均值和方差将数据标准化,计算其核矩阵及熵值大小;

③ 取累计熵贡献率为99%对应的特征值和特征向量,建立DKECA模型;

④ 计算CS统计量以及控制限CSlimit.

2) 在线监测的具体步骤如下:

① 将在线数据引入相同的时间延迟系数l,并根据离线数据的均值和方差进行标准化处理;

② 将在线数据投影到DKECA模型上,计算CSnew统计量;

③ 比较测试数据的CSnew统计量是否超过控制限,从而判断该数据是正常数据还是故障数据.

3 仿真结果与分析

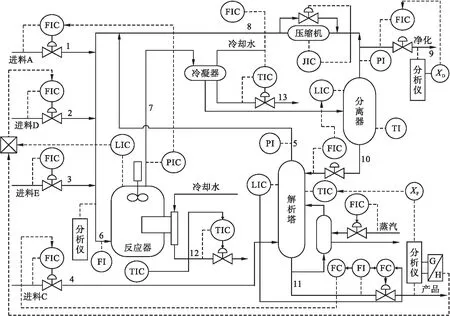
图2 TE过程流程图Fig.2 Flow chart of TE process

为了有效地对使用不同方法的模型进行评估,本文采用故障检测率(fault detection rate,FDR)和误报率(false alarm rate,FAR)对检测结果进行分析.

(12)

(13)

将KPCA、KECA、DKPCA和DKECA方法分别运用到TE过程中,并对这4种方法的检测效果进行对比.在KPCA和DKPCA中,采用传统的SPE统计量对故障进行检测,而在KECA和DKECA中,采用CS统计量.在进行建模时,选择的时间延迟系数为3,通过引入动态特性的方式,有效地降低系统相关性对故障检测的影响.在KPCA和DKPCA中使用95%的累计方差贡献率选取保留的主成分数,而在KECA和DKECA中由于其特有的数据转换方式,只选取1个主成分就能够达到99%的累计熵贡献率.通过这种选取主成分的方式,能够大大减少方法的计算量和复杂度.

对于TE过程中发生的故障,其中有一些明显的故障通过PCA和KPCA等方法就能够取得良好的检测效果,对于一些不明显的故障,大部分故障检测方法都不能取得较好的检测效果.因此,本文选取比较有代表性的一些故障,如故障2、4、5、6、11和18进行仿真实验.其中,故障2、4、5和6是阶跃类型,故障11是随机变化类型,故障18是未知类型.

故障4和故障11都是反应器的冷却水入口温度发生异常,前者是阶跃故障,后者是随机变化故障.以这两个故障为例进行分析,其检测结果分别如图3～4所示.其中,图3a、4a为KPCA使用SPE统计量的检测结果,图3b、4b为KECA使用CS统计量的检测结果,图3c、4c为DKPCA使用SPE统计量的检测结果,图3d、4d为DKECA使用CS统计量的检测结果.从图3～4中可以看出,KECA-CS和DKPCA-SPE比KPCA-SPE的检测结果均有一定的提升.由于KECA方法通过熵值选取主成分能充分地利用数据集中的信息,使得故障检测更加准确,而DKPCA方法能够有效减小数据集的时刻相关性,但是对故障检测效果的提升程度并不十分明显.DKECA方法结合这两种方法的优点,其检测结果取得了明显的提升.在前160个正常数据中,DKECA算法只有个别数据出现了误报,而且后800个故障数据中也仅有很少的故障数据没有被检测出来.

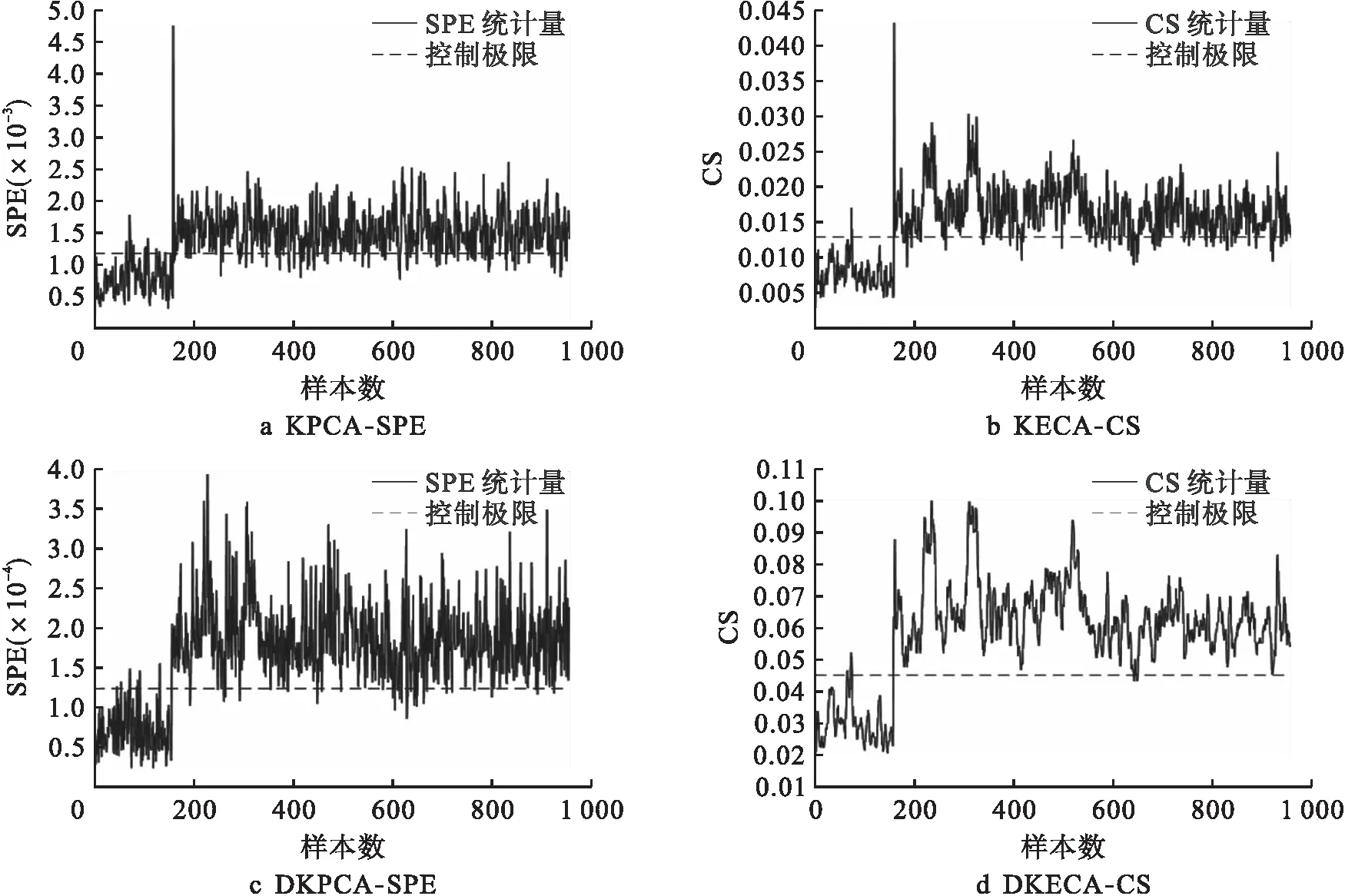
图3 故障4的检测结果Fig.3 Detection results of fault 4

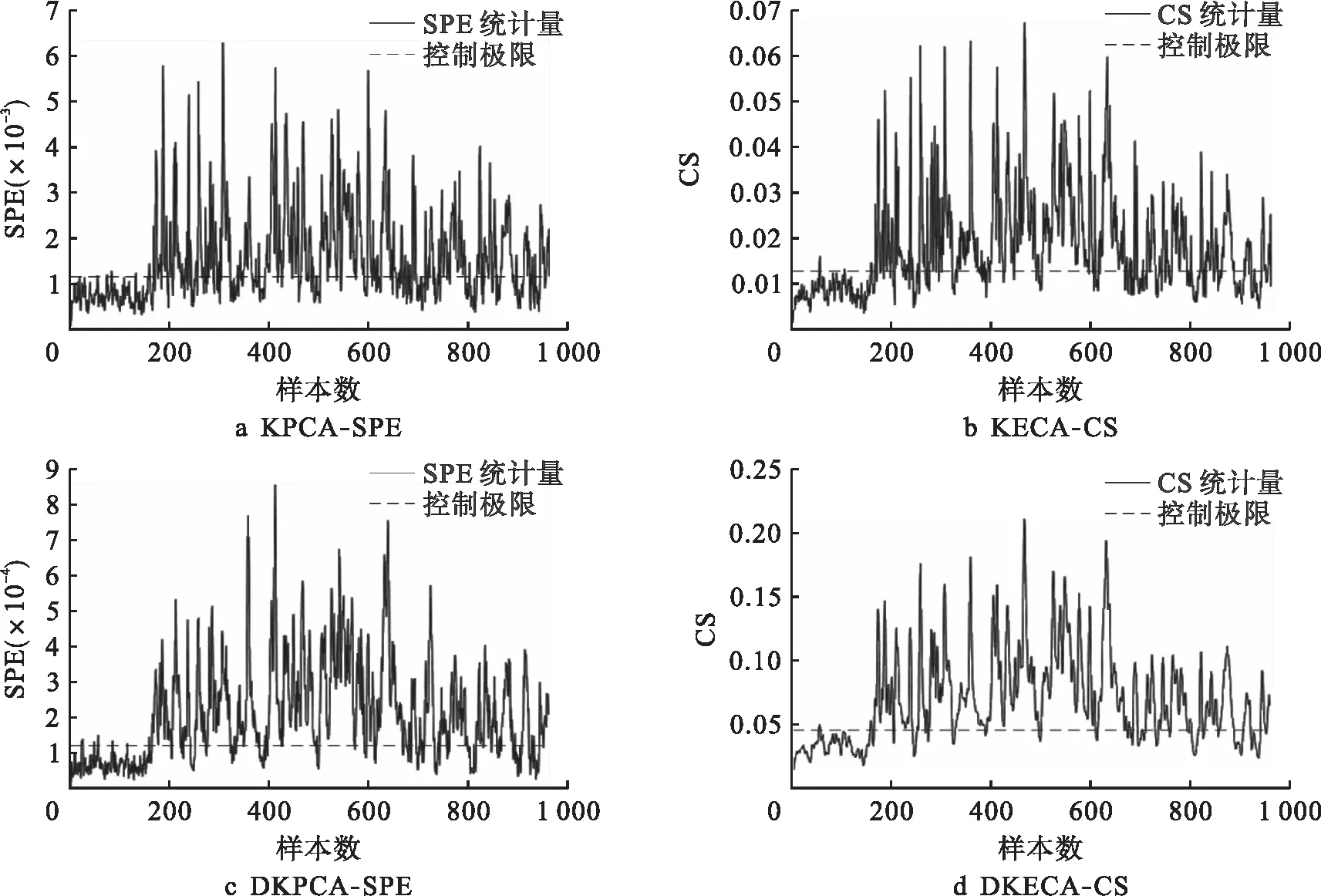
图4 故障11的检测结果Fig.4 Detection results of fault 11

为了对DKECA方法的检测效果进行进一步的分析,统计TE过程的故障检测结果如表1所示.从表1中可以看到,DKECA方法在6种故障中都取得了最高的故障检测率,而误报率均小于5%.由于DKECA方法引入了时间延迟系数,考虑样本的时刻相关性,能够提取过程的动态变化信息,但是由DKECA获得的主成分中仍然保留了一定的自相关性,导致其误报率相对于KECA方法有略微的增加.其中故障5是冷凝器冷却水入口温度的阶跃故障,在TE过程的闭环控制之下经过短暂的波动之后就回到了正常水平,因此各种方法都难以取得较好的检测效果.但是,DKECA方法的检测效果取得一定程度的提升.从表1中可以看出,DKECA方法能够在保持较低误报率的基础上,有效提升故障检测效果.

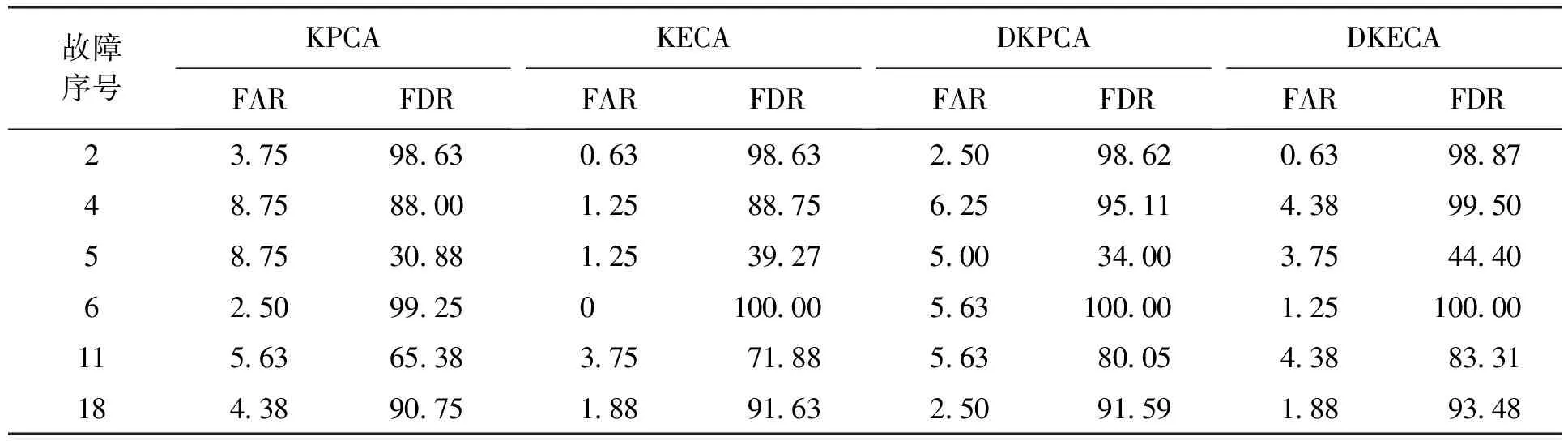
表1 TE过程故障检测结果Tab.1 Fault detection results of TE process %

4 结 论

针对非线性和动态工业过程,在KECA方法的基础上,本文提出一种动态KECA的故障检测方法.通过引入时间延迟系数,考虑样本的时刻相关性,对采集正常数据的动态特性进行分析,建立DKECA模型,并根据该模型对工业过程数据进行故障检测.在检测指标上,选择了基于角度的CS统计量,与传统的SPE统计量相比,具有较好的表现.在TE过程中与KPCA、KECA和DKPCA等方法进行对比,验证了本文所提出的DKECA方法在故障检测方面具有较好的效果.