基于迁移学习算法的电力数据挖掘模型
2023-10-10刘锦明赵学花
易 庚, 何 琳, 刘锦明, 赵学花
(国网新疆电力有限公司 经济技术研究院, 乌鲁木齐 830000)
随着我国电力需求的不断增长,电网运行环境日益复杂,电力行业面临着艰巨的建设任务[1-4].在此背景下,保障电力系统稳定地运行具有重要的战略意义[5-9].为了实现这一目标,电网的控制与调度人员需要获取各个种类、多设备和大规模的实时数据,即实现电网数据的实时挖掘[10].然而,传统的数据挖掘技术较难深入地表征电网数据的典型特征,从而难以满足现代智能化电网的实际需要.
近年来,国内外众多学者通过引入多种人工智能技术,大幅度优化了电力系统的故障检测和诊断技术.MA等[11]基于划分网络提出了使用多反向传播的故障诊断和检测算法;PENG等[12]利用粗糙集理论,提出了适用于分布式馈线且具有定位功能的故障诊断技术;ZHU等[13]基于Noisy-Or和Noisy-And节点的贝叶斯网络,提出了具有一定推导与预测能力的故障诊断模型;BHATTACHARYA[14]与柴尔烜等[15]结合小波变换和神经网络算法,提出了适用于中压直流船载电力系统的故障诊断模型.然而,以上模型及算法通常无法处理较大规模的数据.为了进一步提高实时智能电网的数据利用率,优化故障检测和诊断效率,文中利用电力故障信息,基于栈式稀疏自编码器和循环神经网络,实现了智能电网故障的检测与诊断.结合负荷数据和聚类分析算法设计智能电网的负荷预测模型,提出基于迁移学习的电力数据挖掘模型.相关仿真结果表明,本文所提模型具有更高的数据利用率与更优的数据挖掘效果.
1 故障检测
为了精确地检测出智能电网中的故障,文中提出了基于主成分分析(principal component analysis,PCA)和支持向量机(support vector machine,SVM)的栈式稀疏自编码器,克服了传统神经网络易陷入局部最小的缺陷.
1.1 栈式稀疏自编码器
栈式稀疏自编码是一种基于多层自编码器的训练方法,具备强大的深度学习能力.从函数逼近的视角来看,该训练方法结构可以实现多种数学函数的功能.令h表示故障检测中的隐藏层神经元,x表示故障检测的输入数据,其基本结构如图1所示.
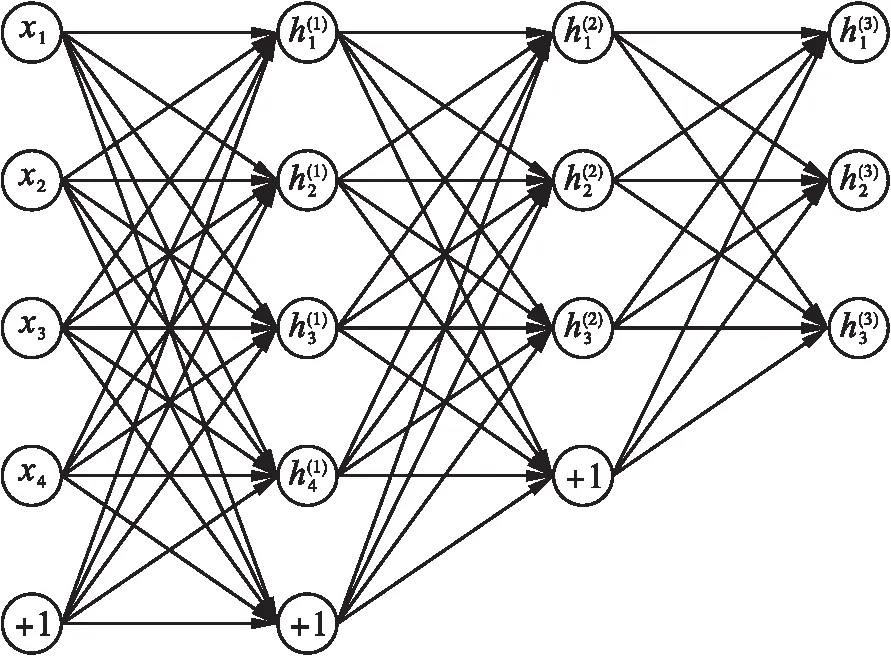
图1 栈式稀疏自编码器的基本结构Fig.1 Basic structure of sparse trestle self-encoder
在工作过程中,栈式自编码器可以通过训练以多种非线性的形式表示大规模数据.假设e表示网络中各个神经元的权重系数,n0与ni分别表示自编码器的输入层和第i个隐藏层的单元数量,Wi表示第i个隐藏层的输入系数,Hi表示第i个隐藏层的系数.

(1)
(2)
(3)
1.2 故障检测模型
基于具有强大非线性表示能力的栈式稀疏自编码器,提出了基于PCA和SVM的改进故障检测模型,模型具体工作流程如图2所示.

图2 基于PCA和SVM故障检测模型工作流程Fig.2 Workflow of fault detection model based on PCA and SVM
为了更加精确地检测电力系统存在的故障,首先,故障模型需要采集系统的电力数据,并形成正常样本、故障样本和无标签样本.在此过程中,电流数据可以反映电力线路的工作状态,常被用作故障检测的输入样本.同时,为了保证故障提取的有效性,模型在采集数据时还应该保留一定的滑窗时间.其次,模型需要对采集的样本数据进行必要的预处理,即对线路电流大小进行标准化转换,形成无量纲数据,方便后续的处理.最后,将转换后的数据输入栈式稀疏自编码器,进行逐层的无监督式预训练,形成相应的训练集和测试集数据,并通过引入经典的机器学习算法,执行精确的故障检测.
2 故障诊断
为了克服电力系统存在的故障信息较少的缺点,本文通过引入长短期记忆网络,降低了数据挖掘过程的拟合程度,从而实现故障数据的精确诊断.
2.1 长短期记忆网络
针对循环神经网络存在的梯度消失问题,文中引入了长短期记忆网络模型.利用误差的梯度指标进行反向传播,其基本原理如图3所示.

图3 长短期记忆网络的基本原理图Fig.3 Basic principle diagram of long-term and short-term memory network
图3中,U与M分别为长短期记忆网络的输入门和输出门的中间参数,令xi与yi分别表示长短期记忆网络的第i个输入和输出,si表示长短期记忆网络的第i个状态.则根据图3的结构,第i个隐藏单元误差梯度的计算表达式为
(4)
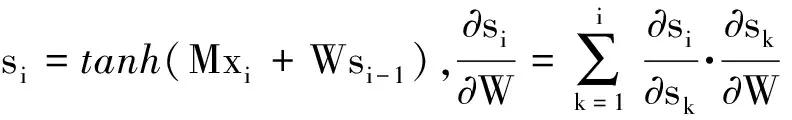
(5)
基于上述循环神经网络改进方法,令φ和g分别表示sigmoid和tanh函数,通过添加输入门、输出门与单元结构等设备实现改进的长短期记忆网络单元结构,如图4所示.
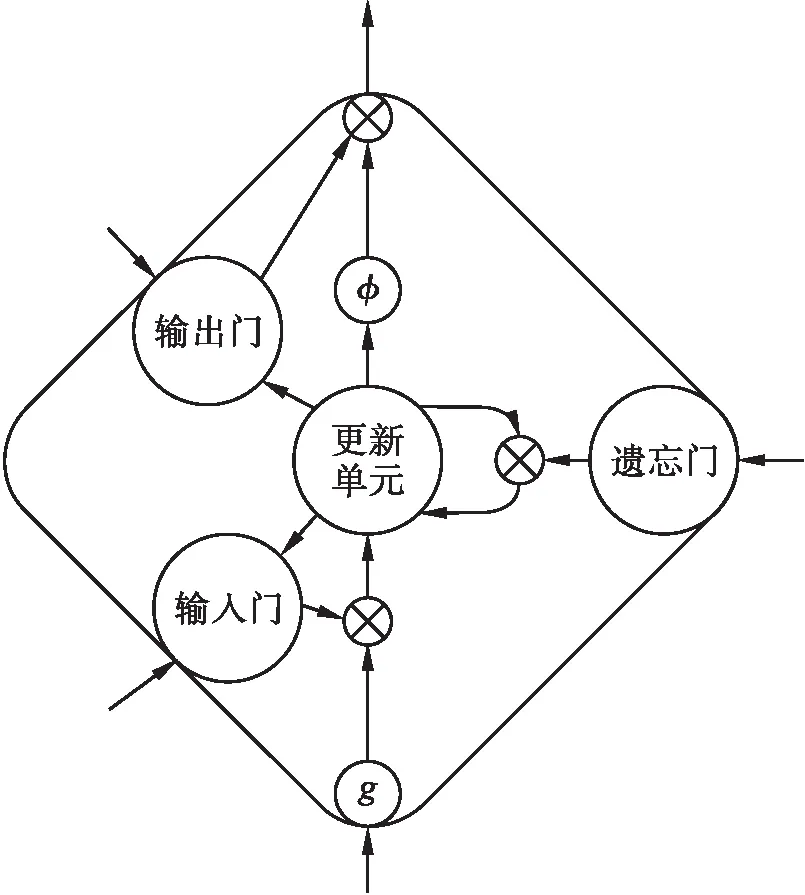
图4 长短期记忆网络的单元结构Fig.4 Unit structure of long-term and short-term memory network
2.2 故障诊断模型
为了克服传统神经网络梯度消失的问题,在长短期记忆网络的基础上,提出了具有精确诊断能力的电力系统故障诊断模型,其一般架构如图5所示.
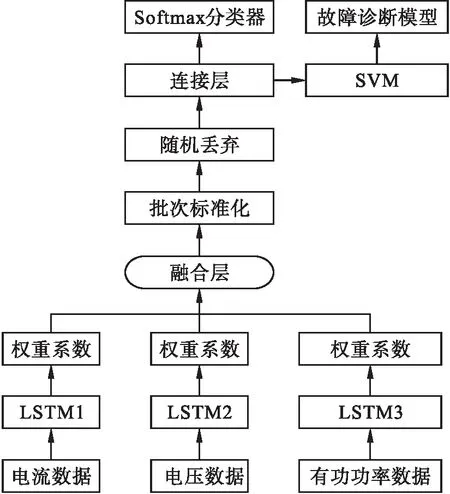
图5 电力系统故障诊断模型架构图Fig.5 Architecture of power system fault diagnosis model
本文提出的故障诊断模型工作过程如下:
1) 利用电流、电压和功率等数据样本,获取过电流、设备缺陷和外力破坏的具体故障数据;
2) 利用标准化预处理技术,通过引入K-CV等检验方法,实现训练集和测试集的划分;
3) 根据LSTM输入的维度,分割训练集和测试集数据,从而获取多个时间节点的子序列,确定LSTM网络的输入数据;
4) 使用训练集数据对LSTM网络和分类器进行必要的训练,实现电力数据特征的提取和融合;
5) SVM分类器全面接受全连接层提供的数据特征,从而实现最终的故障分类和诊断,系统反馈相应的预防和检修措施.
3 数据挖掘模型
在故障检测与诊断模型的基础上,为了进一步提高数据的利用率和挖掘效果,本文利用最大均值差异理论,提出了适用于智能电网的电力数据挖掘模型.
3.1 最大均值差异
为了解决电力数据存在的双样本检验问题,文中在电力数据挖掘模型中引入了最大均值差异算法,即利用特定的连续函数计算多个样本的均值差,从而辨别不同的分布.假设f∈F是样本空间连续函数集中的某个函数,p∈P与q∈Q分别是服从数据集X和Y的具体数据,P与Q的数据规模分别为c和d,则这两者的最大均值差异值定义为
(6)
令I表示数据集的内积函数,经过推导可知最大均值差异值的求解方法为
(7)
3.2 数据挖掘网络
基于迁移学习算法提出了具有实际应用意义的电力数据挖掘模型,实际工作流程如图6所示.
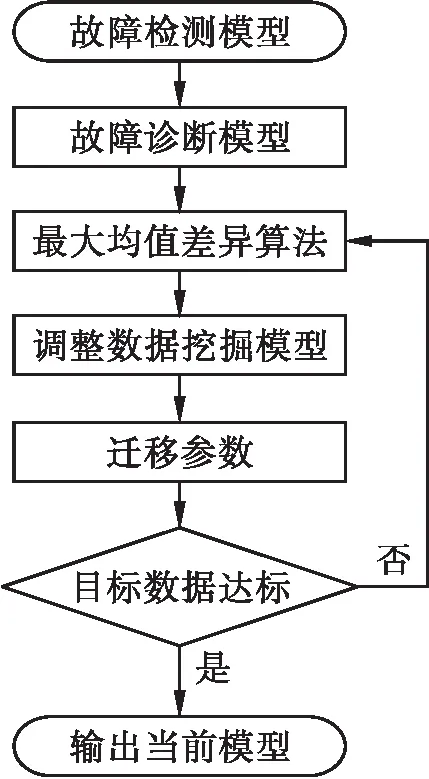
图6 电力数据挖掘模型工作流程图Fig.6 Workflow of power data mining model
首先利用栈式稀疏自编码和改进循环神经网络对故障检测与诊断模型进行必要的数据处理及训练.其次利用最大均值差异相关理论对电力系统中的源数据与目标数据之间的差异进行精确的评估和分析,从而获取模型的调整依据,完成数据挖掘模型的参数迁移.然后利用测试集的标准数据与模型的目标数据进行计算和比较,若目标数据处于允许的误差范围内,即达到标准数据,则输出电力数据挖掘模型;否则,继续使用最大均值差异算法对模型中的参数进行必要的调整.
4 仿真结果与分析
为了验证电力数据挖掘模型的可行性,本文利用智能电网中的真实电力数据对数据挖掘模型进行了必要的仿真与性能分析.
4.1 仿真条件
为了充分衡量电力数据挖掘模型的性能,选取2016~2018年国家电网新疆区域的电力历史数据,数据主要包含36条支线线路和大量用电客户的电气量使用数据,形成了规模分别为36 000和9 000的训练集和测试集.仿真设备选用型号为R730、内存为32 GB的戴尔架式服务器,其中央处理器为E5-2630 V3,主频为3.4 GHz,GPU型号是NVIDIA Tesla K40M.此外,本文还对数据挖掘网络的具体结构进行了必要的设置,具体情况如表1所示.

表1 数据挖掘网络的结构参数设置Tab.1 Structure parameter settings of data mining network
4.2 数据分析
对基于粗糙集的数据挖掘模型与所提电力数据挖掘模型进行对比分析.粗糙集理论从不同的角度导出多个层次的信息集和规则集,从而完成电力数据的挖掘,所以作为一种经典的电力数据挖掘算法被用于本文的仿真实验对比和验证分析中.
在电力数据挖掘模型中,源数据和目标数据之间的分布差异受最大均值差异值影响较大,如果最大均值差异值较大,则数据之间的分布差异将增大,从而影响电力数据的挖掘效果;另外,如果用户数据的采样间隔发生变化,则数据挖掘模型的负荷预测效果将产生剧烈的变化,所以,数据采样间隔和最大均值差异值对数据挖掘的最终效果具有较大的影响.通过设置不同的最大均值差异值和不同的时间采样间隔进行两种模型的仿真实验.计算这两种模型获取数据与原始数据之间的平均绝对百分比误差,从而精确地衡量模型的性能表现,相应的结果如图7、8所示.

图7 平均绝对百分比误差随最大均值差异值的变化曲线Fig.7 Variation curves of average absolute percentage error with maximum mean difference
由图7可知,随着最大均值差异数值的增大,两种模型获取电力数据的平均绝对百分比误差值均不断增大,但所提模型的数值始终小于传统模型.这说明本文所提模型在设置相同的最大均值差异值时,具有更高的精确度.由图8可知,若设置不同的数据采样间隔,则两种模型的平均绝对百分比误差值均呈现先减小后增大的趋势,但本文所提模型的误差值幅度也始终小于传统数据挖掘模型.综上所述,在相同的最大均值差异值和数据采样间隔的条件下,与传统数据挖掘模型相比,基于迁移学习的电力数据挖掘模型可以获取具有更高精度的电网数据.
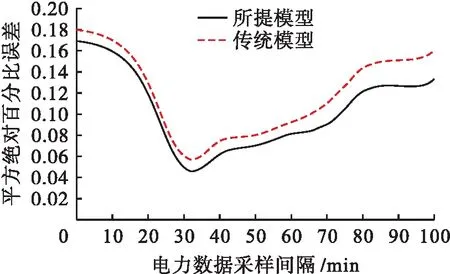
图8 平均绝对百分比误差随电力数据采样间隔的变化曲线Fig.8 Variation curves of average absolute percentage error with power data sampling intervals
5 结 论
基于栈式稀疏自编码器和长短期记忆网络结构,本文提出了一种具有故障检测和诊断等多种功能的电力数据挖掘模型.相关仿真证明,该模型具有较高的数据挖掘精确度.然而关于该电力数据挖掘模型的研究仍处于初始阶段,且存在较大的发展和提升空间,如何将该电力数据挖掘模型融合到智能电网的负荷预测中,这是未来需要重点研究的问题,也是下一步的研究方向.
