基于填充式ECT传感器的图像重建

颜 华, 梁丽卓, 王 艳

(沈阳工业大学 信息科学与工程学院, 沈阳 110870)

电容层析成像技术[1-5](electrical capacitance tomography,ECT)是一种基于电容传感机制的过程层析成像技术.利用该技术可实现封闭管道或反应器内部具有不同介电常数的介质分布的可视化测量.ECT技术具有非侵入、成本低、安全性好等优点,在化工流化床、石油管道流、颗粒包覆反应器等领域具有广阔的应用前景[6-7].

目前ECT技术测量的管道或反应器截面通常为圆形.但工业中存在大量非规则截面的管道或设备,例如制备核燃料包覆颗粒的小倾角、复杂角度和结构的多环斜孔式流化床[8].采用ECT系统对非规则截面管道成像时,通常要用已知介电常数的材料填充非规则管道与传感器内壁间的空隙.因高温、腐蚀等原因无法将测量极板安装在管道或反应器外壁的场合也存在同样的空隙填充问题.目前已有学者对相关问题展开研究,利用有限元仿真,陈昭等[8]研究了不同背景的敏感场强度、归一化电容值矩阵、填充区介电常数大小及图像重构算法对重构图像的影响,给出了填充材料介电常数应和重建区高介电常数一致的测量建议.但文献[8]建模时采用的是忽略非规则管道壁的简化模型,而且对于常见的双管流和三管流图像重建效果欠佳.

非规则管道壁是不容忽视的存在,为此本文将填充式ECT传感器的敏感区域划分成重建区、管道壁和填充区3个部分,建立了完整的有限元分析模型.从灵敏度计算、空满场标定、填充介质选取及正问题模型的改进等方面着手,降低了非重建区对重建质量的不利影响,并最终给出一套重建质量更高、工程上更容易实现的测量方法.

1 ECT基本原理

ECT系统由ECT传感器、数据采集系统和成像计算机3部分组成.ECT图像重建属于逆问题研究,通常借助正问题模型求解.离散化、线性化处理后的ECT正问题模型[9]通常表示为

λ=SG

(1)

式中:λ为M×1维的归一化电容值向量;S为M×N维的归一化灵敏度矩阵;G为N×1维的归一化介电常数向量,又称灰度向量;M为ECT传感器输出的电容值数目;N为重建区域划分的像素数目.

对于式(1)所示的正问题模型,Landweber迭代算法第k次迭代给出的灰度向量[13]为

(2)

式中:P(·)为0、1阈值处理算子,该算子将大于1的灰度值置为1,小于0的灰度值置为0;α为控制收敛速率的增益因子,本文取α=2/βmax,其中,βmax为STS的最大特征值.

2 填充式ECT传感器的图像重建

2.1 填充式ECT传感器的有限元模型

本文以六边形管和12极板ECT传感器为例,研究非规则截面的ECT成像.六边形管的轴心与ECT传感器绝缘管道的轴心重合.六边形管的内径为78 mm,壁厚为2 mm,用硬纸板手工制作而成.ECT传感器由金属屏蔽罩、绝缘管道和柔性覆铜板组成.屏蔽罩内径为134 mm,材质为不锈钢,其作用是屏蔽外界电磁干扰.绝缘管道的内径为104 mm,壁厚为3 mm,材质为有机玻璃.柔性覆铜板粘贴在绝缘管道的外壁,其上用刻蚀的方式形成12个均匀布置的243 mm×800 mm的铜极板.12个极板分别用电缆连接至数据采集系统的BNC端子,极板周围的覆铜和极板上、下两端的覆铜与地连接形成接地条和接地环.接地条用来降低相邻极板间的电容值,而接地环的作用是压缩传感器的敏感空间.为行文方便,本文称ECT传感器绝缘管道内,即内径为104 mm的圆内为敏感区域,六边形管内为重建区,两管道间的空隙为填充区.重建区内两相介质的相对介电常数分别为εl和εh.图1a给出了填充式传感器截面图.在COMSOL Multiphysics多物理场中建立了该传感器的有限元模型,图1b给出了典型的有限元网格剖分图.

2.2 归一化灵敏度矩阵

本文用电场强度法计算灵敏度分布.用规则小网格将ECT系统的敏感区域离散成3 844个正方形像素,即N=3 844.ij极板对在像素e处的灵敏度为

(3)

式中:Ei(x,y)和Ej(x,y)分别为极板i和极板j作为激励极板,当施加激励电压U时,其余极板处于地电位时的电场强度分布;Ae为像素e所在区域.计算出N个单元的灵敏度值后,可将灵敏度矩阵表示为

(4)

对灵敏度矩阵s进行归一化,得到归一化灵敏度矩阵S.通常ECT传感器的灵敏度分布是在敏感区域内只有空气的条件下计算的,本文称相应的归一化灵敏度矩阵为常规灵敏度矩阵,记为SCG.但对于填充式ECT传感器而言,为减少软场误差,灵敏度计算时敏感区域内不应该只有空气,还应该有填充材料以及非规则管道壁,本文称如此计算的归一化灵敏度矩阵为非规灵敏度矩阵,记为SFG.ECT传感器的敏感场不均匀,存在正、负敏感区,所以介质分布对灵敏度分布的影响相当复杂.高介电常数介质的存在不仅会改变其所在区域的灵敏度值,也改变了其他区域的灵敏度值,使其出现或正或负的变化[15].图2以相对的1～7极板为例,给出了常规灵敏度图、填充材料介电常数εTC=1(即空气)时的非规灵敏度图以及εTC=6时的非规灵敏度图.比较图2a和图2b可以看出,非规则管道壁(介电常数设置为2.5)的存在使得非规则管道内的灵敏度略有降低;对比图2b和图2c可以看出,高介电常数填充物的出现会使得非规则管道内的灵敏度略有提升.

图2 1～7极板对灵敏度图Fig.2 Sensitivity maps of 1 to 7 plate pairs

归一化可以使测量数据无量纲化且在一定程度上减少各种干扰对电容值的影响,本文采用的归一化表达式为

(5)

对于填充式ECT传感器而言,敏感区域内非规则管道壁和填充区不是要重建的对象,但其存在却改变了ECT传感器的电容输出值.为借助归一化方法降低管道壁和填充材料对重建的影响,本文针对重建区定义空、满场,即将非规则管内充满低介电常数介质(本文为空气,εl=1)视为空场,充满高介电常数介质视为满场.本文将这样定义的空、满场称为非规空、满场,对应的归一化电容向量称为非规归一化向量,记为λFG.

2.4 正问题模型

本文将ECT传感器的敏感区域(3 844个像素)划分成3个区域:六边形管内的重建区(1 800个像素)、六边形管壁(180个像素)以及两管道之间的填充区(1 864个像素),对应的灰度向量分别是1 800×1维向量GCJ、180×1维向量GGB和1 864×1维向量GTC.抽取SFG矩阵中的对应列,可以得到这3个区域对应的归一化灵敏度矩阵,分别是66×1 800维向量SCJ、66×180维向量SGB和66×1 864维向量SST.至此,可以写出填充式ECT传感器的非规正问题模型为

λFG=SFGG=SCJGCJ+SGBGGB+STCGTC

(6)

假设填充区介质的相对介电常数为εTC,本文将GTC视为元素皆为(εTC-εl)/(εh-εl)的1 864×1维向量.再令

(7)

则有

λJF=SJFGJF

(8)

式中,λJF、SJF、GJF分别为降维后的归一化电容向量、归一化灵敏度矩阵以及灰度向量.式(8)为本文所建立的降维填充式ECT非规正问题模型,简称降非模型.降维后方程的数目不变,但未知量数目由3 844锐减至1 980,一定程度上改善了逆问题不适定性.对于正问题模型进行降维处理能够在一定程度上改善灵敏度矩阵的病态问题.

2.5 逆问题求解

本文用Landweber迭代法求解逆问题.正问题模型分别采用降非模型、非规模型和常规模型.降非模型是非规模型的降维版本,常规模型和非规模型的差别只在于灵敏度矩阵计算和空、满场标定方法上.

利用降非模型得到的灰度向量GJF为1 980维,而利用常规模型、非规模型得到的灰度向量G为3 844维.从GJF或G中提取重建区域对应的1 800维向量GCJ,即可得到非规则管道内归一化介电常数分布.

3 仿真数据验证

利用COMSOL Multiphysics所获取的仿真电容数据,对所提方法的有效性进行了验证.测试原型包括半层流、高层流、核心流、二管流、三管流和三角流等6种流型.测试原型中红色表示低介电常数相,介电常数为εl=1;蓝色表示高介电常数相,介电常数为εh=6.为定量评价重建图像的质量,引入相关系数CC以及图像误差RE.相关系数CC越接近于1,图像误差RE越小,重建质量越好,相关系数和图像误差的定义详见文献[9].表1～3给出了填充区分别用εl和εh填充时6种测试原型的无噪声仿真电容数据所对应的重建图像、相关系数和图像误差.

表1 重建图像(无噪声仿真数据)Tab.1 Reconstructed images (noiseless simulation data)

表2 相关系数(无噪声仿真数据)Tab.2 Correlation coefficients (noiseless simulation data)

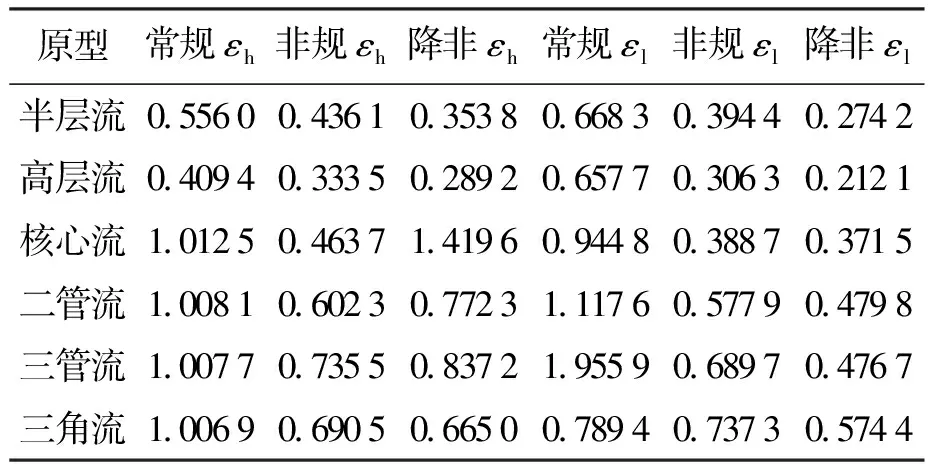
表3 图像误差(无噪声仿真数据)Tab.3 Image errors (noiseless simulation data)

为研究填充介质介电常数对重建质量的影响,本文将填充区的介电常数εTC依次设置为1、2、3、4、5、6,受篇幅限制,仅以三管流原型为例,给出了填充区分别用6种介电常数填充时无噪声仿真电容数据对应的重建结果.由于εl填充和εh填充分别对应εTC=1和εTC=6,故表4～6给出εTC为2、3、4、5这4种情形的重建图像、相关系数及图像误差.

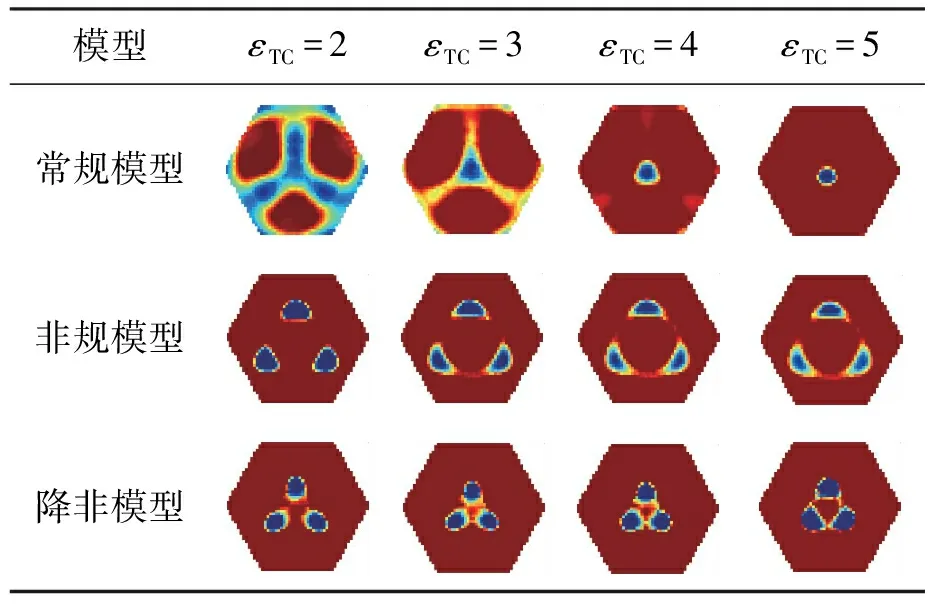
表4 εTC对重建图像的影响Tab.4 Influence of εTC on reconstructed images

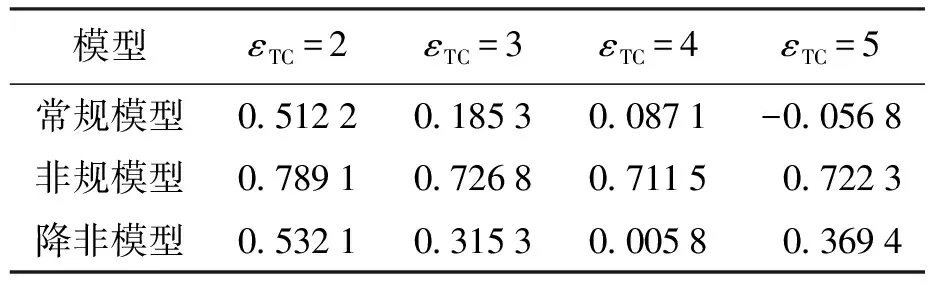
表5 εTC对相关系数的影响Tab.5 Influence of εTC on correlation coefficient

表6 εTC对图像误差的影响Tab.6 Influence of εTC on image error

由表1～6给出的重建误差和重建图像可以看出:1)当填充介质介电常数为εl时,非规模型优于常规模型,因为非规模型中灵敏度计算和空、满场标定方法降低了非重建区对重建质量的不利影响;降非模型优于非规模型,因为对非规模型的降维处理降低了逆问题不适定性.2)填充区介电常数越大,重建质量越差,但填充区介电常数对不同模型的影响有明显差异;εh填充非规模型不能正确地重建出三角流的基本特征;εh填充降非模型不能正确地重建出核心流、三角流的基本特征;εh填充常规模型不能正确地重建出核心流、两管流、三管流、三角流的基本特征.综上,采取εl填充的降非模型重建质量最优,其重建误差最小,重建图像也最接近原型.

与εh填充相比,εl填充还有两个明显的好处:1)工程上更容易实现,只要不对空隙进行填充就可实现;2)εl填充材料的介电常数估值比εh更准确.基于上述考虑,对于填充式ECT传感器的图像重建问题,本文所提出的测量方法是:εl填充,降非模型及Landweber迭代法求逆.

为检验所提方法的抗噪性能,在有限元仿真电容值中分别添加6%、10%及15%的随机噪声.为保证抗噪性能评价的可靠性,对每一种测试原型的每一个噪声水平都生成40组含噪仿真电容值.表7给出所提方法在不同噪声水平下的重建图像.表8、9分别给出了所提方法在不同噪声水平下对应的相关系数及图像误差,其数据是40组图像误差的平均值.

表7 重建图像(含噪声仿真数据)Tab.7 Reconstructed images (including noise simulation data)

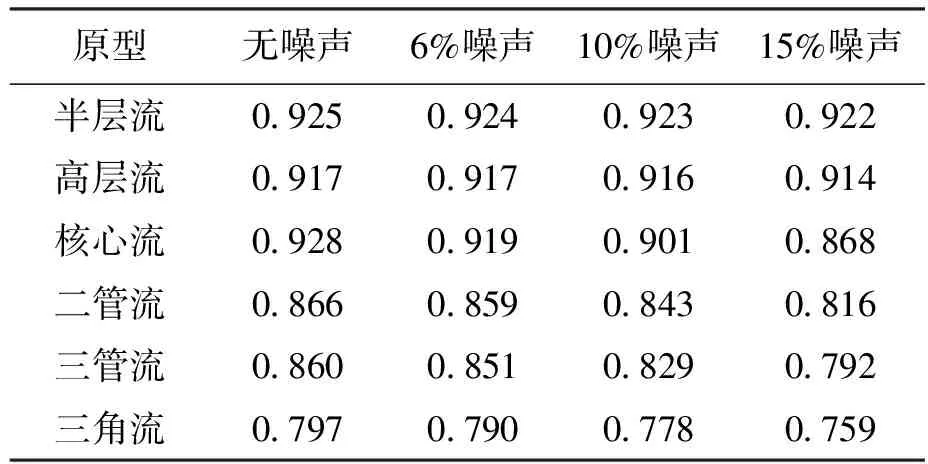
表8 相关系数(含噪仿真数据)Tab.8 Correlation coefficients (including simulation data)

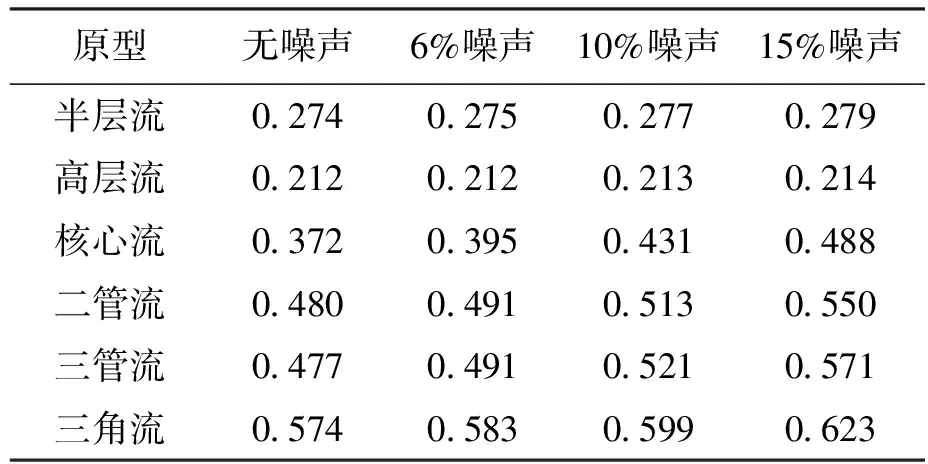
表9 图像误差(含噪仿真数据)Tab.9 Image errors (including simulation data)

由表7～9可以看出,随着噪声水平的增加,重建图像的误差略有增加,但增加的幅度并不大,即所提方法具有良好的抗噪能力.

4 实测数据验证

为进一步验证所提方法的有效性,采用ITS公司的ECT系统获取实测电容数据.图3为实验系统及空满场标定示意图.实验时低介电常数介质为空气,高介电常数介质为聚苯乙烯珠.分别对核心流、半层流及侧边流进行了实测数据验证.表10给出了非规模型和降非模型所对应的重建图像.表11、12分别给出了重建图像的相关系数和图像误差.可以看出,降非模型的重建质量明显优于非规模型的重建质量.

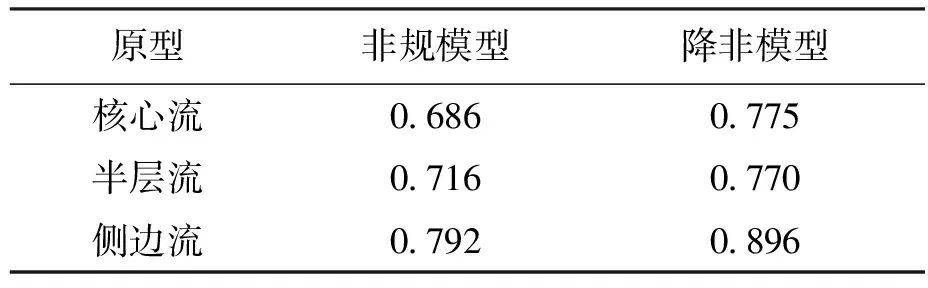
表11 相关系数(实测数据)Tab.11 Correlation coefficients (measured data)

表12 图像误差(实测数据)Tab.12 Image errors (measured data)

图3 实验系统Fig.3 Experimental system

5 结 论

ECT传感器截面通常为圆形.当用于非规则截面管道,或因为高温、腐蚀等因素无法将极板直接安装在管道外壁时,通常用已知介电常数的介质填充两管道间的空隙,形成填充式ECT传感器.本文研究相应的图像重建问题,主要结论如下:

1) 对于填充式ECT传感器,敏感区域内非规则管壁和填充材料不是重建的对象,但其存在却改变了敏感场的灵敏度分布和传感器的输出值.计算灵敏度时敏感区域内有填充材料和非规则管壁的存在,且空、满场标定针对重建区域进行,这种不同于常规的灵敏度计算法和空、满场标定法,可有效降低非重建区对重建质量的不利影响.

2) 将已知填充区介电常数和灵敏度矩阵拆分处理,建立降维的ECT正问题模型,可以减少逆问题的不适定性,提高重建质量.填充区介电常数与重建区低介电常数一致时,重建质量更好.