考虑差异化负荷特性的基于改进遗传算法的供电可靠性分析

王 勇, 金飞宇, 张子信, 王麒翔, 车延博

(1. 华北电力大学 电气与电子工程学院, 河北 保定 071003; 2. 国网辽宁省电力有限公司 经济技术研究院, 沈阳 110004; 3. 天津大学 电气自动化与信息工程学院, 天津 300072)

随着电力系统规模的不断扩大与控制监控系统的智能化发展,电力系统的运行条件逐渐复杂化,故对其进行可靠性评估所需考虑的变量及随机因素[1]在不断增长.而大幅增长计算量也导致了分析难度的增加.经过多年的研究和探讨,国内外专家学者在电力系统可靠性分析方面均取得了一定的成果,并提出了不同的模型构建及数据分析方法[2-4].现阶段工程中常用的可靠性评价方法主要有解析法、仿真法等.LIU等[5]提出一种基于蒙特卡罗法的电网可靠性分析方法.通过改进蒙特卡罗模型的抽样方法,实现了电力系统状态概率分布的优化,并提升了可靠性分析速度和准确性.李莉等[6]针对电网运行可靠性评估中难以计及系统的高阶故障状态影响、时效性及准确性等问题,提出一种将解析法与蒙特卡洛法结合的改进混合法.利用解析法处理系统的N-1阶故障,结合蒙特卡洛法累计计算实现系统的运行可靠性评估,但未考虑负荷差异化所带来的影响.丁明等[7]在高渗透率可再生能源接入配电网的大背景下,同时考虑光伏、风电、储能以及V2G的负荷模型,提出基于序贯蒙特卡洛随机模拟方法,对配电网可靠性进行评估,然而可靠性评估效率和准确性仍有待提升.

现有智能电网的可靠性评估不仅要满足时效性和高准确性的要求,还需考虑负荷差异化特性.因此,提出了一种考虑差异化负荷特性基于改进遗传算法的供电可靠性分析方法,其特点如下:1)为了充分挖掘负荷的差异化特性,利用模糊C均值聚类算法(FCM)进行特征提取,并设计了“耦合系数”用于量化负荷间的匹配程度;2)由于遗传算法存在易陷入局部最优的问题,因此利用小生境技术对其进行改进,以保持种群进化的多样性,实现全局收敛.

1 基于聚类算法的负荷差异化特性提取与匹配

1.1 负荷差异化特性提取

FCM是一种基于划分的聚类算法[8-9],该聚类方法能够最大化同一簇的相似度,同时保证不同簇之间的最小相似度.FCM聚类算法主要根据样本中不同类别的隶属度值进行柔性的模糊分类,将其用于差异化负荷特征的提取,具体步骤如下:

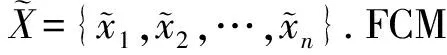
(1)

式中:k为分类数目;O为区域的聚类中心矩阵;F为模糊矩阵,其元素fij为隶属度,即第i个样本属于第j类程度;m为模糊加权指数;d为欧氏距离.

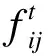
(2)

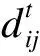
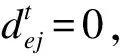
(3)

3) 负荷差异化特性提取的合理性取决于所计算聚类数目k的有效性函数φ(k),当其值达到最大时提取性能最优,求解结束.φ(k)的计算表达式为

(4)

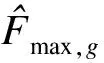
1.2 负荷差异化匹配分析

基于FCM完成差异性负荷聚类后,需要对各类负荷进行匹配度研究,以充分挖掘各类负荷间的峰谷耦合潜力,便于优化调度不同类型负荷的分配,进而提高区域的供电可靠性.因此,利用“耦合系数”来量化不同负荷的峰谷耦合程度,并计算出合适的匹配结果.“耦合系数”计算表达式为

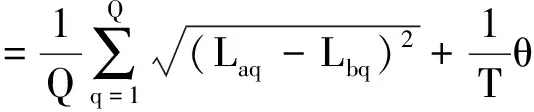
(5)

式中:ϑ为正指标;Laq与Lbq分别为归一化后第a类负荷与第b类负荷一天中峰谷重合时间段内第q时刻的负荷值;Q为日负荷曲线中峰谷重合的时刻数;T为日负荷曲线总时间;θ为负荷一天内的峰谷重合时间,其中负荷峰值出现时间为典型日最大负荷出现的时段,负荷低谷出现时间为典型日最小负荷出现的时段[10-11].

根据对应时间段的“耦合系数”即得两类负荷曲线间的峰谷耦合程度.同时考虑不同负荷曲线在时序上的特性互补程度,计算负荷间的峰谷重合时间占比[12].不同负荷在一天内的平均欧式距离越大,峰谷重合的时间占比便越高,而用于优化组合的潜力也相应越强.ϑ值越大,差异化负荷匹配的效果就越明显.在进行区域内供电可靠性分析时,需优先考虑将ϑ值大的负荷组合划分到同一区域内,使负荷最大化地接入每一供电区域.

2 供电可靠性分析模型

电网的供电可靠性受多个因素的共同影响,基于选取的可靠性指标和负荷差异化匹配程度,利用改进遗传算法进行优化搜索,以得到最佳的负荷耦合方案,从而实现供电可靠性的最大化.

2.1 供电可靠性指标

供电可靠性分析需要保证其全面和综合性,目前,常用的供电可靠性评价指标主要有:供电可靠率(power supply reliability,PSR)、用户平均停电时间(average interruption time of users,AIT)、用户平均停电次数(average interruption frequency of users,AIF)、用户平均短时停电次数(average short-time interruption frequency of users,ASTIF)、系统停电等效小时(equivalent hour of system interruption,EHI).各指标的赋值通过熵权法进行,保证了权重的客观性和综合性.设有J个评价样本,I个供电可靠性评价指标,则熵权法表示为

(6)

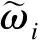
(7)

式中,γ1、γ2分别为客观和主观的权重系数,均取为0.5.由此,可得样本的供电可靠性综合评价值为

(8)

2.2 改进遗传算法

2.2.1 遗传算法

遗传算法(genetic algorithm,GA)作为一种智能优化搜索算法,基于生物自然选择规律,集成了基因遗传学原理,具有较好的搜索性能和应用前景[13-14].GA算法在寻优过程中具有明显的优势,如算法本身是并行的,可同时搜索解空间内的多个区域,加快了搜索速率,并具备广泛的适应性.但GA算法也存在一定的缺陷:

1) 由于基本GA算法的各迭代方案是直接进行遗传的,所以可能会存在结果丢失的现象,无法获得全局最优解;

2) GA算法的收敛性和种群个体的多样性受算法交叉、变异概率影响极大,传统方法通常根据具体问题来静态设置交叉、变异概率,因此不能针对具体情况及时作出调整,从而导致GA算法早熟,陷入局部最优;

3) 基本GA算法通常采用轮盘赌方式进行选择操作,而该种方式对于适应度高的个体具有较好的倾向性,因此容易导致高适应度个体种群激增,甚至主导种群进化方向.

2.2.2 小生境改进遗传算法

针对GA算法自身特点,为保证最优解的多样性,利用小生境技术对算法进行优化,同时兼顾全局性和收敛速度[15].其中小生境技术通过将子代个体逐一分类,并从中选择若干适应度高的作为一个新的种群,再由种群之间的杂交、变异操作产生新一代个体.而选择操作则通过预选择、排挤或者共享机制完成.改进算法基本思想为:通过共享函数的调节实现群体内个体适应度的调节,根据调整后的适应度值,GA算法可进行保证群体多样性的选择运算.

群体中不同个体之间的相似度可以通过共享函数反映,当不同个体之间相似度高时,共享函数值较大;反之,函数值偏小.共享度是种群内该个体与其他个体之间共享函数值之和,是个体在群体中共享程度的度量,可表示为

(9)

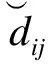
φit(X)=φ′it(X)/ψi

(10)

适应度值的大小可以控制个体的遗传概率,通过限制群体中个别个体的数量激增,保证了群体的多样性,实现了小生境的进化环境.

2.3 基于改进遗传算法的供电可靠性分析

利用小生境改进GA算法分析区域电网的供电可靠性,具体过程如下:

1) 生成初始种群.将初始种群规模设为100,既可满足计算时间的要求又尽可能地扩大了搜索范围.

2) 构建适应度函数.以供电可靠性最大化为目标设计适应度函数,其计算表达式为

φit(x)=1/Θi

(11)

3) 小生境和精英策略选择操作.在算法初期,选择操作利用小生境共享函数完成;后期则通过精英策略来保留最佳个体,最终收敛得到全局最优解.

4) 自适应交叉、变异操作.改进GA算法中提出了一种新的自适应交叉、变异概率计算方式,其可随着问题的变化而作出调整,保证算法的收敛性.自适应交叉Pc、变异概率Pm计算表达式为

(12)

(13)

式中:φmax、φavg分别为群体中最大、平均适应度值;φ′、φ分别为交叉个体中较大适应度值和变异个体适应度值.

5) 优化负荷供电结构.根据寻优算法得到最佳的负荷耦合方案,通过调整各类负荷供电的时间段以及电量,实现供电可靠性最大化.

3 实验结果与分析

实验基于一个3馈线18节点的区域电网展开,其中供电网络总负荷为28.7 MW+j17.3 MVar,基准功率和电压分别为100 MVA和10 kV,设计额定电压为23 kV,18条支路为5种负荷供电,分别是居民类、商业类、工业类、教育类、行政类,且有4个联络开关用于负荷优化调度.通过查阅历史负荷数据,以6 h为一个数据采样点,可得出如表1所示负荷数据.

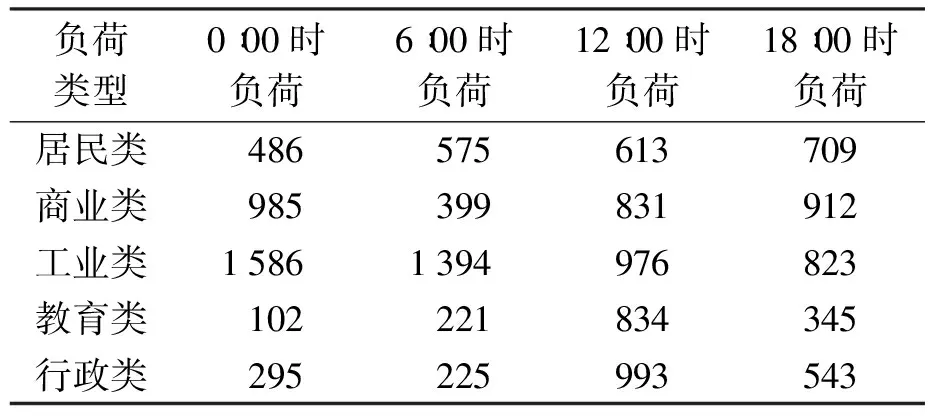
表1 区内电网历史负荷数据Tab.1 Historical load data of power grid in region kW

此外,改进遗传算法的基本参数设置如下:初始种群大小120,染色体长度32,迭代次数为200次,Pc、Pm分别为0.8和0.2.

3.1 改进遗传算法性能分析

基于小生境技术改进的GA算法能够弥补传统GA算法的不足,其中两者对于供电可靠性的分析结果如图1所示.

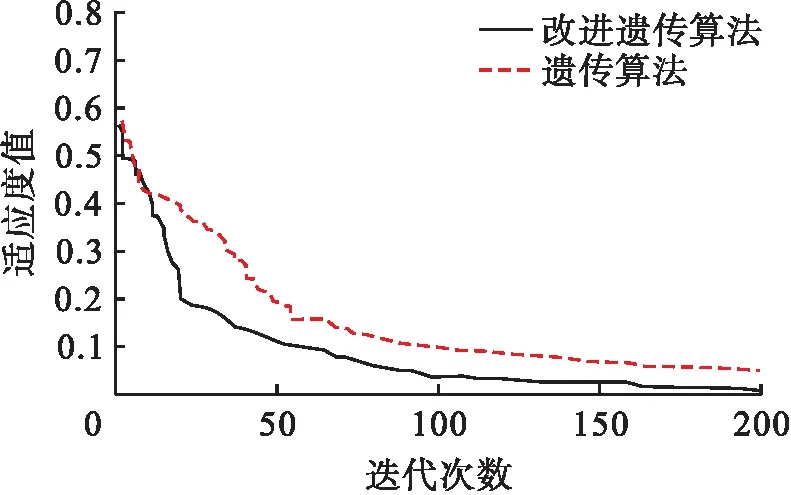
图1 不同算法的寻优结果Fig.1 Optimization results of different algorithms

由图1可知,在迭代初期两种算法的适应度值相近,即优化效果大致相同,但随着迭代的进行,改进GA算法的适应度值快速下降.这是因为前期采用小生境的共享函数进行选择,加快了全局收敛速度.此外,改进GA算法在迭代100次后趋于收敛,且适应度值较小.而传统GA算法在迭代150次后仍未收敛,由于其交叉、变异概率固定,导致收敛效果不理想.综合来看,小生境改进遗传算法在供电可靠性分析中具有一定的优势.

3.2 差异化负荷的优化匹配结果

利用FCM对实验中涉及的5种常见负荷进行聚类分析,具体的负荷聚类结果如图2所示.

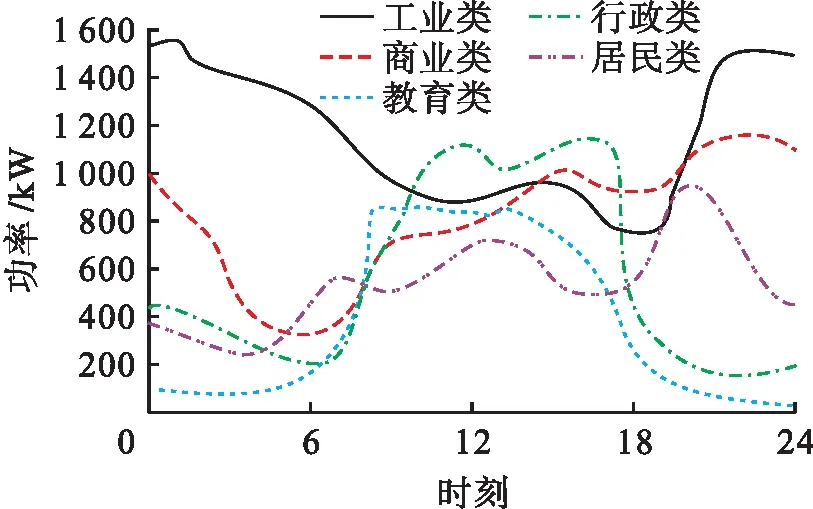
图2 负荷曲线聚类结果Fig.2 Clustering results of load curves

由图2可知,行政类和教育类具有明显的工作属性,8∶00到17∶00达到负荷峰值.居民类和商业类受人们日常活动的影响,19点之后的用电量增加.而工业类用电量则较大,为了减少生产成本,合理利用分时电价,20∶00～4∶00的用电量偏高.由此可见,各类负荷间存在优化匹配的潜力.对比表1历史负荷数据可知,聚类分析结果与实际负荷变化趋势相同,且负荷大小情况相近.

结合图2的聚类结果,计算负荷间的耦合系数ϑ来评估不同负荷间的峰谷耦合程度,从而进行差异化负荷优化匹配,以实现区域内供电单元的最优划分,耦合结果如图3所示.

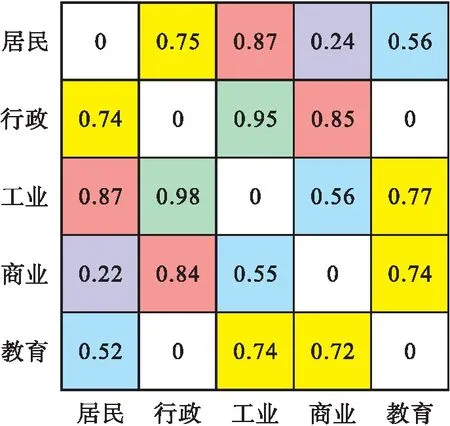
图3 差异性负荷间的峰谷耦合结果Fig.3 Peak valley coupling results among differential loads

由图3可知,每种负荷均有对应的最佳匹配.在供电区域划分时,应优先将ϑ值最大的组合划分到同一时间区块内.如行政和工业的耦合程度较高,ϑ超过了0.90,两者可优化组合,实现削峰填谷.但在实际的规划中,由于环境等因素的限制,可能会对最终的结果造成一定的影响,因此考虑将负荷间ϑ值排在前3位的组合均作为候选组合,以最大程度地挖掘负荷间的调节潜力,实现系统的稳定供电.

3.3 供电可靠性对比分析

为了论证本文所提模型的性能,将其与文献[5]、[6]、[7]中的模型进行对比,4种模型得到的供电可靠性分析结果如表2所示,其中综合评价值为百分制.

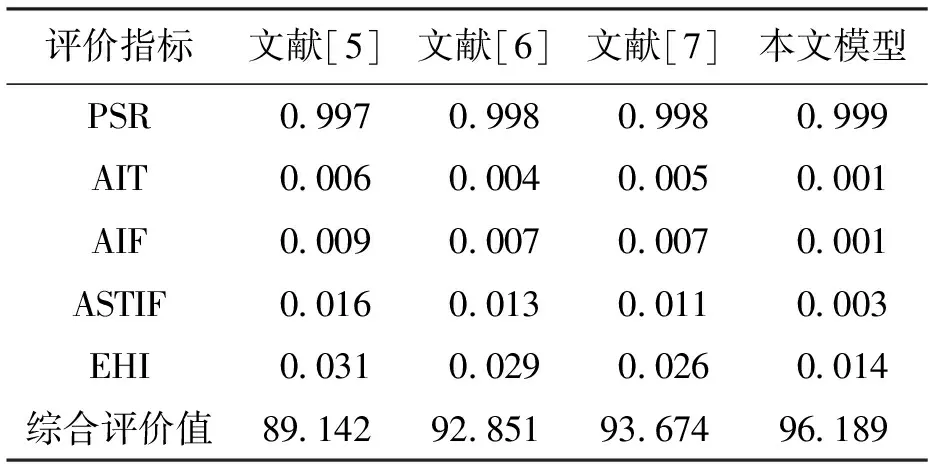
表2 不同模型的供电可靠性指标值Tab.2 Power supply reliability index values of different models

从表2可以看出,相比于其他模型,本文所提模型的各指标值更为理想,且综合评价值达到了96.189.所提模型利用FCM算法完成差异化负荷的聚类分析,得到负荷间的耦合度,并基于改进遗传算法进行负荷调度方案寻优,以实现区域供电可靠性的最大化.文献[5]基于蒙特卡罗法进行电网可靠性分析,单一分析方法的处理效果并不理想,因此EHI达到了0.031,且综合评价值仅为89.142.文献[6]和文献[7]均对蒙特卡罗法进行了改进,提升了供电可靠性的分析效果,但由于缺乏差异性负荷的考虑,其综合评价值较所提模型降低了3.338和2.515.综合来看,所提模型能够最大化提高供电可靠性,满足实际电网运行需求.

4 结 论

随着电力体制改革逐渐深化,供电可靠性的高低将直接影响电力工业的整体水平,为此,提出了一种考虑差异化负荷特性基于改进遗传算法的供电可靠性分析模型.其中针对FCM算法提取的差异化负荷设计了一种“耦合系数”,以量化不同负荷的匹配程度,并基于改进遗传算法优化求解得到供电可靠性最大化的负荷调度方案.实验结果表明,行政和工业的耦合程度较高,ϑ超过了0.90.所提模型的综合评价值达到了96.189,能够为实际运用提供一定的理论基础.由于文中考虑的网架结构是确定的,而不同的网架供电可靠性也有所区别,因此在后续的研究中,将针对不同网架结构验证所提模型的分析性能,以确保其普适性.