改进势场蚁群算法下的物料传输平台路径规划
2023-10-10顾金凤郎家伟
孙 宇,唐 炜,谭 啸,顾金凤,郎家伟
江苏科技大学 机械工程学院,江苏 镇江 212003
在物联网、智能制造等新兴技术的推动下,传统物流业正朝着信息化、现代化方向发展,但实际生产中大多数传输分拣系统仍采用人工或半自动的操作方式,整体自动化水平并不高[1]。货物传输路径的长短是衡量系统工作效率的一个重要指标。通常根据环境信息的已知或未知,将路径规划分为全局路径规划[2]和局部路径规划[3]。不同环境下采用的路径规划方法也有所差别,对于物料传输系统来说,全局规划常用算法主要有A*算法[4]、蚁群算法[5]等,而局部规划通常采用动态窗口法[6]、人工势场法[7]等算法。近年来,国内外不少学者对物料分拣设备与路径规划算法进行了相关的研究。文献[8]提出了一种基于STM32的物流分拣小车,其上安装有机械臂以实现货物的抓取功能,但物流小车货物运输量较小且机械臂的抓放与定位精度要求较高,不适用于大规模物料的运输。文献[9]研究了一种柔性送料系统,并采用人工势场法完成路径规划,但其传输的物料尺寸具有一定范围,主要为微小、精密型的零件,系统及算法的应用领域有所限制。文献[10]采用改进的A*算法与人工势场法对分拣平台进行路径规划,但仅分析了整体模块出现故障时的情况,并未对全向轮系故障状况进行细分,算法的工程化应用存在局限性。文献[11]在路径规划中通过引入最优解和最差解的方法改进了传统蚁群算法,收敛速度有所提升,但并未对局部路径中存在障碍物的情况进行深入研究,环境适应性仍可进一步提升。文献[12]采用改进的快速搜索随机树算法进行包裹分拣的路径规划,缩短了传输路径的长度,但仿真时未考虑所传输包裹的实际尺寸,当包裹距离障碍物过近时,可能会出现路径干涉情况。文献[13]将改进的人工势场法与蚁群算法相结合,降低了路径规划时算法陷入局部最优的概率,但路径中仍存在转角过大、拐点数偏多等缺点,机器人运动的平稳性有待提高。
针对上述物料分拣方式与路径规划算法存在的问题,本文面向模块化物料传输平台采用改进势场蚁群算法(improved ant colony system algorithm with potential field,ⅠACSPF)完成了物料传输的路径规划。相比文献[8]和[9],平台由于结构特殊性,使其可以传输数目较多的物料,且物料自身尺寸具有较大的调整范围。相比文献[10]和[11],平台路径规划环境建模时,对障碍物的设定已细分到单个全向轮的辐射区域,并且考虑到局部路径规划时出现障碍物的情况。相比文献[12]和[13],在全局静态路径规划中,通过优化启发函数并设计因子自适应更新策略改进了传统蚁群算法,提高算法搜索过程的针对性,加快收敛速度,降低了陷入局部极小值的概率;在局部动态路径规划中,考虑物料本身尺寸,通过引入距离调节因子和模糊斥力点解决了传统人工势场法中的目标不可达和局部最优问题,提升了算法的灵活性与实效性。仿真结果表明,ⅠACSPF 算法能有效缩短物料传输路径,并且减少不必要的拐点,使物料传输路径更为平滑,从而改善了物料传输的平稳性。故对物料传输平台及其的路径规划方面展开相关研究,具有重要的理论价值与实际意义。
1 平台结构分析与环境建模
1.1 平台结构分析
新型物料传输平台由若干个正六边形模块构成,其上预留有各模块的安装位置,可随模块数量的增加而拼接扩展。为便于物料传输,各模块体采用蜂窝状的布局形式,并嵌入安装3 个呈120°对称分布的全向轮;每个全向轮的转速与转向均由对应的直流电机进行独立控制;任意3个相邻全向轮的几何中心组成尺寸完全相同的等边三角形。在物料传输过程中,通过对各全向轮的转速与转向进行协同控制,可在不改变传输平台机械结构和控制系统硬件的前提下,柔性地调整物料的传输路径,从而实现物料的灵活分拣。如图1为物料传输平台基本结构示意图。

图1 物料传输平台基本结构Fig.1 Basic structure of material transmission platform
1.2 环境建模
建立传输平台模型是进行后续路径规划的基础。常用的地图构建方法有可视图法、栅格法等[14-15]。其中,可视图法通过连接各障碍物顶点形成可视线的方法规划最优路径,但在障碍物数量增多时,算法运行效率会明显降低;而栅格法具有数据结构简单、容易构建、便于分析等优点,本文采用其对传输平台进行地图建模。如图2为物料传输平台栅格化模型图,其中,黑色栅格表示障碍物即不可行区域,白色栅格表示无障碍物即可行区域。
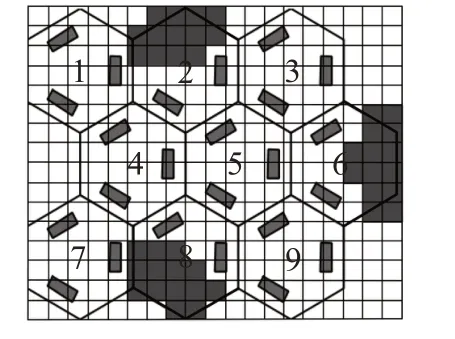
图2 传输平台栅格化模型图Fig.2 Grid model diagram of transmission platform
在物料传输过程中,若模块中某全向轮出现故障,需将其归为障碍物进行处理。障碍物区域的划分如图3所示。在此将六边形等分成三个以全向轮为中心的五边形即工作区域,见图3(a)。当轮子发生故障时,其所在的工作区域均当作不可行区域;若不可行区域未占满一个栅格时,仍视为占满一个栅格,黑色栅格为故障轮子的辐射区域,见图3(b)。

图3 障碍物区域划分示意图Fig.3 Schematic diagram of dividing obstacle area
本文在进行路径规划时,因平台具有特殊的模块化结构及轮系布局形式,故物料传输存在较强的约束性,物料在栅格法中的移动须遵守以下规则:
(1)只能在本栅格周围的8个相邻栅格进行移动,且路径不能与黑色栅格相交,但黑色栅格四角可作为接触点。
(2)规定栅格边长为1个单位,以限定目标每次移动的路径长度为1或个单位,即对应向两边或对角移动。
(3)在传输分拣过程中,物料至少与3 个无故障的全向轮保持接触,以保证物料的全方位稳定传输。
(4)对于最佳路径的选取,要求物料从起点到目标点的移动距离最短,不能碰撞障碍物,且要保证路径不能重复经过同一栅格,否则会造成不必要的能量损失。
2 全局路径规划
2.1 传统蚁群算法
传统蚁群算法(ant colony optimization,ACO)是由Marco Dorigo 等人于1991 年首次提出,该算法模拟了自然界中蚂蚁的觅食行为[16]。具体原理如下:
蚂蚁i(i=1,2,…,a)在八邻域的可移动范围内,根据信息素的浓度来选择下一移动节点,设Pimn(t)为t时刻蚂蚁i从当前节点m移动到下一节点n的概率,则:
式中,τmn(t)为t时刻两节点之间的信息素浓度;ηmn(t)为距离启发函数,ηmn(t)=1/dmn,dmn为两节点之间的欧式距离;α、β分别为信息素启发因子与距离期望函数因子,二者分别影响τmn(t)与ηmn(t)在蚁群搜索路径时所占的重要程度;Ai为蚂蚁i可移动的节点集合。
当一代蚂蚁路径规划结束后,需判断是否达到终止条件即最大迭代次数,若不是则更新路径上的信息素含量。具体为:
式中,Δτmn为两节点之间的信息素浓度之和,为两节点上信息素浓度的增量,ρ为信息素挥发因子,Li为蚂蚁i经过的路径长度,I为信息素增强系数。
2.2 改进蚁群算法
ACO 在全局路径规划中虽有诸多优势,但也存在算法收敛时间长、易陷入局部最优等问题[17-18]。针对上述问题,设计了一种改进蚁群算法(improved ant colony optimization,ⅠACO)进行全局路径规划。
2.2.1 优化启发函数
在ACO 运行的初始阶段,信息素在地图上分配较均匀,整体浓度差别不大,导致蚁群不能依照路径中信息素浓度的高低判别较优前进方向,无法准确搜寻到可行路径。为此在原启发函数的基础上引入下一节点n与目标点节点D之间的欧式距离dnD以及动态权重系数进行优化,可提升算法的收敛速度并降低陷入局部最优的概率,具体公式为:
式中,η′mn(t)为优化后的距离启发函数,x、y为节点的横、纵坐标,bk为算法当前迭代次数k中最佳路径经过的模块数量,B为平台的总模块数量。λ1、λ2为动态权重系数,初始值皆为1,满足λ1+λ2=2 关系,且随着bk的增加,λ2的权重占比相应提高。
2.2.2 因子自适应更新策略
ACO 中信息素启发因子、距离期望函数因子及信息素挥发因子是不变的,但考虑到在算法运行初期,路径中的信息素浓度过低,地图信息匮乏,导致蚂蚁寻路的随机性扩大;而后期又因为信息素积累过多,限制了蚂蚁搜寻的范围,易使算法陷入局部最优。可见,如选取不变因子则不利于最佳路径的选取,需设计一种因子自适应更新策略,具体如下:
式中,K为算法总迭代次数,u0、u1及u2为常量且大于1,α′为改进后的信息素启发因子(初始值为2.4),β′为改进后的距离期望函数因子(初始值为9.7),ρ′为改进后的信息素挥发因子(初始值为0.9)。α′、β′及ρ′的变化曲线如图4所示。
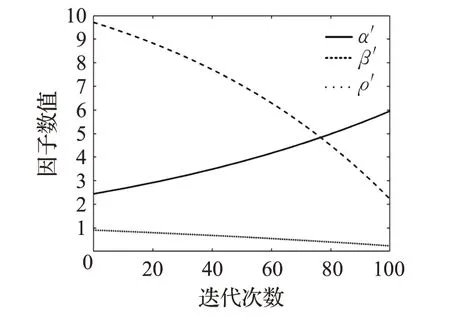
图4 因子变化曲线Fig.4 Change curve of factor
在算法初始阶段,为使蚂蚁尽可能搜寻到更多的可行路径,α′权重占比不宜过高,β′权重占比不宜过低,且两者的变化幅度较小、变化速度较慢,以保证β′的重要程度,ρ′在自身取值范围内的值不应过小,此时有利于扩大蚁群的搜寻范围;而随着迭代次数的增加,α′权重提升,β′权重降低,两者变化幅度逐渐增大,变化速度逐渐提升,ρ′数值逐渐降低,负反馈效果削弱,路径上的信息素随之增多,信息素浓度对路径选取的重要程度也相应提升;当达到一定迭代次数时,蚁群将选择信息素含量最高的路径作为最佳路径。故ⅠACO可降低蚁群搜索的盲目性,提升算法收敛速度并降低陷入局部最优的概率。
2.2.3 算法步骤
ⅠACO流程如图5所示,具体步骤如下:

图5 ⅠACO流程图Fig.5 ⅠACO flow chart
步骤1采用栅格法对传输平台进行二维环境建模。
步骤2初始化算法相关参数,设置起点与目标点。
步骤3放置a只(一代)蚂蚁。
步骤4为每只蚂蚁确定当前候选道路集,开始寻路。
步骤5通过优化后的启发函数与自适应因子改进传统概率模型,确定蚂蚁下一移动位置。
步骤6判断每只蚂蚁是否完成路径,若是则执行下一步操作;否则返回步骤4。
步骤7记录每只蚂蚁的路径长度,选出a只蚂蚁中的最佳路径,更新最佳路径。
步骤8判断是否达到最大迭代次数,若是则选出最佳路径;否则更新信息素,返回步骤3。
3 局部路径规划
传统人工势场法(artifificial potential fields,APF)是通过引力与斥力的合力控制物料的移动,存在以下问题[19-20]:
(1)在障碍物与目标点间距离过近的情况下,会产生目标不可达问题。因当物料抵达目标点位置时,虽引力减小至零,对物料无作用,但此时障碍物产生的斥力不为零,致使物料无法及时停止,出现来回震荡的现象。
(2)当障碍物对物料的斥力与目标点对物料的引力产生的合作用力为零时,物料会陷入局部最优,无法抵达目标点位置。图6(a)、(b)分别为单个与多个障碍物造成局部最优情况的示意图。其中,单个障碍物产生的斥力Freq和多个障碍物产生的合斥力Freq(合)均与目标点产生的引力Fatt大小相等且方向相反。

图6 局部最优情况示意图Fig.6 Schematic diagram of local optimal situation
针对上述问题,采用了一种改进的人工势场法(improved artifificial potential fields,ⅠAPF)来进行局部路径规划。
3.1 引入距离调节因子
对于目标不可达的问题,通过在APF的障碍物斥力场模型中引入距离调节因子进行解决,优化后的斥力场函数与斥力如下:
式中,ρ0为障碍物作用的最大距离;ρNg为距离调节因子,表示物料与目标点之间的距离;N为常数,根据经验取N=2;c为斥力增益系数;q、q0分别为物料当前位置与障碍物位置;ρ(q,q0)表示q和q0之间的欧式距离;Freq1、Freq2的方向分别为从障碍物指向物料与从物料指向目标点,具体见图7。

图7 改进后物品受力情况Fig.7 Stress situation of improved articles
由于改进的斥力势场中引入了ρgN,使得物料在向目标点的传输过程中,路径上受到的Fatt与Freq(合)的大小同时在一定范围内减小,且仅当物料抵达目标点的位置时,两者才同时减为零,即目标点为最小势能点,从而避免了震荡现象的产生。
3.2 增设模糊斥力点
为解决物料陷入局部最优问题,仍需对人工势场模型进一步优化。主要通过物料近期位置变化是否过近,判断其是否陷入局部极小值;若是,则增设模糊斥力点,额外产生的斥力使物料所受合力改变,从而逃离局部极小值点。具体增设步骤如下:
步骤1首先以物料中心r为圆心,障碍物作用的最大距离ρ0为半径画圆R1;构造同时经过距离r最近的障碍物点F与起点O的直线l1;记录l1与x轴的夹角θ;判定落在圆R1内的障碍物个数b。若b=1 执行步骤2,若b=j(j=2,3,…)则执行步骤3。
步骤2障碍物个数为1个。记录物料中心r与F之间距离L1;以r为圆心,L1为半径画圆R2;构造经过F与r的直线l2;将l2以圆心r为基准,正或逆时针旋转θ角构造直线l3。l3与圆R2的交点中距离F较远的节点为模糊斥力点Q,如图8所示,图中为逆时针旋转。

图8 单个障碍物时模糊斥力点示意图Fig.8 Diagram of fuzzy repulsion points with single obstacle
步骤3障碍物个数为多个。记录距离物料中心r最近的2 个障碍物之间的距离L2,其之间的中心点f及物料轮廓最大尺寸h(已知参数);同时求出F与r之间的距离Lmin;以r为圆心,Lmin为半径画圆R3。
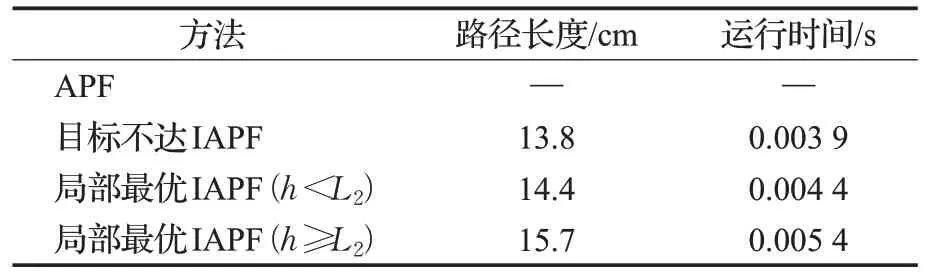
若h 图9 多个障碍物时模糊斥力点示意图Fig.9 Diagram of fuzzy repulsion points with multiple obstacles 在物品的传输过程中,会受到障碍物与模糊斥力点的作用,而ρ0的选取会影响两者的作用范围。ρ0为一个人为给定的阈值,以此来改善算法的局部搜索精度,本文令ρ0=1.5。通过增设模糊斥力点改进算法后,能有效减轻人工势场法中局部最优的问题,并通过仿真验证得出结论:在给定的ρ0情况下,模糊斥力点的增设不会影响算法的局部搜索能力,仍可保证路径的最佳选取,不易导致算法陷入局部最优。 虽然ⅠACO可以规划出一条全局最优路径,但距离障碍物过近时,会出现无法实时避开障碍物或转角过大问题;而ⅠAPF单独路径规划时虽能有效避开障碍物,但由于缺少全局路径信息,规划的路径通常并非最优。故有必要对ⅠACO与ⅠAPF进行融合,采用新的ⅠACSPF算法进行路径规划,以提升物料的传输分拣效率,并减少不必要的拐点,使传输路径更为平滑。 ⅠACSPF流程如图10所示,具体步骤如下: 图10 ⅠACSPF流程图Fig.10 Flow chart of ⅠACSPF 步骤1通过ⅠACO 完成全局路径规划,选出最佳路径。 步骤2记录全局最佳路径上的拐点位置。 步骤3判断相邻两拐点间的距离dmin是否小于等于2 cm。若是,则删除前一拐点,并更新拐点位置。 步骤4调用ⅠAPF,将全局路径中拐点的位置作为局部路径中子目标点的位置以完成路径规划。 步骤5判断局部路径终点是否与目标点位置相同。若是,则输出ⅠACSPF的最佳路径;否则返回步骤4。 为验证本文所述改进算法的有效性,在软件MATLAB R2016b 中进行了路径规划对比仿真实验。其中,黑色栅格区域为人为设定的全向轮故障辐射区域。 搭建20×20的栅格化二维地图环境,设置物料的起点坐标为(0,20),目标点坐标为(20,0)。相关算法的路径规划与收敛曲线对比结果如图11、12所示。 图11 ACO与ⅠACO路径规划对比结果Fig.11 Comparison results of path planning between ACO and ⅠACO 图11(a)采用ACO 进行路径规划,路径拐点多,部分拐角较大,且在图中画圈处从两障碍物中间穿越,在本传输平台上属于不合理路径;图11(b)采用ⅠACO 进行路径规划,路径拐点少、较平滑,算法搜索过程针对性强,且有效解决了出现不合理路径的问题。 由图12可知,ACO收敛曲线波动较大,收敛速度慢且达到总迭代次数后仍未趋于稳定,耗时多,同时该算法易陷入局部最优,选择的路径不是最佳规划路径;而ⅠACO波动较小,收敛速度快,在迭代29次后趋于稳定,耗时少,且选择的路径为最佳规划路径,可使平台的传输分拣效率随之提高。综上,ⅠACO相比ACO的改进是合理且有效的,相关对比结果见表1。 表1 ACO与ⅠACO仿真对比结果Table 1 Comparison results of simulation between ACO and ⅠACO 图12 收敛曲线对比结果Fig.12 Comparison results of convergence curve 可以看出,ⅠACO相比ACO路径长度缩短了10.2%,且运行时间缩短了40.7%,拐点数目减少了35.7%,收敛速度提高了至少71.0%。因此,ⅠACO 在传输平台上具有更强的寻优能力。 当面临未知障碍物时,须采用ⅠAPF 完成局部路径规划,使物料远离障碍物,以提高传输安全性。起点位置标记为□,目标点位置标记为▽。在此分别对物料产生目标不可达问题与陷入局部最优情况进行对比分析,具体如下: (1)在APF作用下,由于目标点附近存在障碍物,物料所受斥力与引力交替增加或减少,使物料无法达到目标点,在目标点附近徘徊形成震荡区域;而ⅠAPF由于引入ρNg,使得目标点处势能值最低,能够顺利到达目标坐标点(9,9),同时相比APF来说,无震荡现象的产生,有效解决了目标不可达问题,此外还提高了路径的规划效率和平滑度。目标不可达时APF与ⅠAPF路径规划对比结果如图13所示,图中画圈处为物料运动轨迹的震荡区域。 图13 目标不可达时APF与ⅠAPF路径规划对比结果Fig.13 Comparison results of path planning between APF and ⅠAPF when target is unreachable (2)当采用APF 时,物料易陷入局部极小值点,此时物料停止运动,无法到达目的地;而当采用ⅠAPF 时,通过增设模糊斥力点能使物料在原局部极小值点处的合力不为零,使物料远离局部极小值点,并成功到达目标点。具体路径规划对比结果如图14所示。 图14 局部最优时APF与ⅠAPF路径规划对比结果Fig.14 Comparison results of path planning between APF and ⅠAPF in local optimization 由图14(a)可知,当物料陷入局部最优且h 以上仿真表明:当面临目标不达问题与局部最优问题时,ⅠAPF通过引入调节因子和增设模糊斥力点进行局部动态路径规划,传输分拣效率更高。具体对比结果见表2。 表2 面临问题时APF与ⅠAPF仿真对比结果Table 2 Comparison results of simulation between APF and ⅠAPF when facing problems ⅠACSPF与图10(b)中ⅠACO的路径规划对比,如图15所示。 图15 ⅠACO与ⅠACSPF路径规划对比结果Fig.15 Comparison results of path planning betweenⅠACO and ⅠACSPF 路径规划初期,ⅠACSPF 勘探能力更强,算法的收敛速度与最小路径长度都有明显改善,这主要因为ⅠACSPF 中改进了启发函数,且ρ′数值较高,以此降低路径上的信息素,减小信息素对未来蚂蚁行为的影响,增加了算法的探索能力;规划中期,由于改进算法中的因子自适应动态变化,使得α′权重占比提升,β′权重占比下降,ρ′数值逐渐降低,加强了信息素浓度对路径选取的影响效果,算法收敛幅度逐渐减小,增强了算法的开发能力;规划后期,ⅠACSPF 也能更快收敛,找到的路径相比改进前也更优。此外,ⅠACSPF 下的物料传输路径长度进一步优化,且运动轨迹整体更为平滑,拐点较少,更符合实际工程应用需要。对比结果见表3。 表3 ⅠACO与ⅠACSPF仿真对比结果Table 3 Comparison results of simulation betweenⅠACO and ⅠACSPF 由表1 与表3 可知,ⅠACSPF 相比ACO 路径长度缩短13.1%,拐点数减少71.4%,故ⅠACSPF 算法在物料传输平台上的寻优与避障能力更强。 本文针对模块化传输平台的路径规划问题,提出了一种改进势场蚁群算法的新型路径规划算法。通过相关仿真分析,得出以下结论:优化启发函数与设计因子自适应更新策略,减少了算法运行时间与产生局部极小值概率。引入距离调节因子和增设模糊斥力点,解决了局部路径中的目标不可达问题,并且能有效避免陷入局部最优的情况。将两种改进算法融合后设计的改进势场蚁群算法,可减少路径中不必要的节点,并降低传输过程中的能量损耗。改进势场蚁群算法的寻优能力更强且规划的路径更加平滑,通过MATLAB 仿真验证了该算法的有效性。 未来工作将考虑面临动态障碍物时,物料将如何有效规避并完成相应的最佳路径规划,提升算法的环境适应性;同时结合实际工程,在更为复杂的环境中完成物料的快速传输工作,进一步验证算法的合理性与有效性。
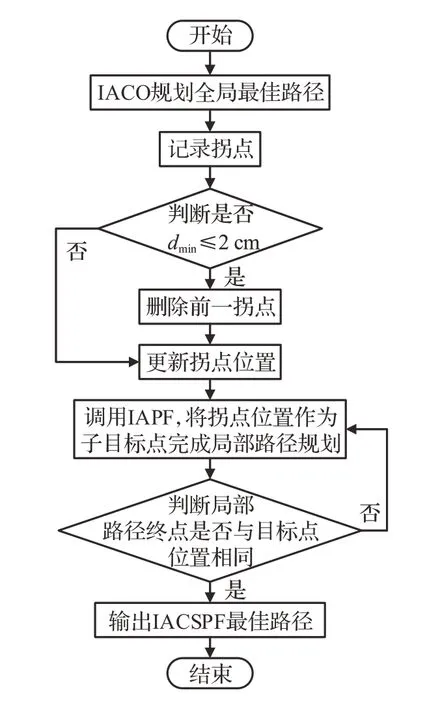
4 IACSPF路径规划
5 仿真分析
5.1 IACO路径规划结果
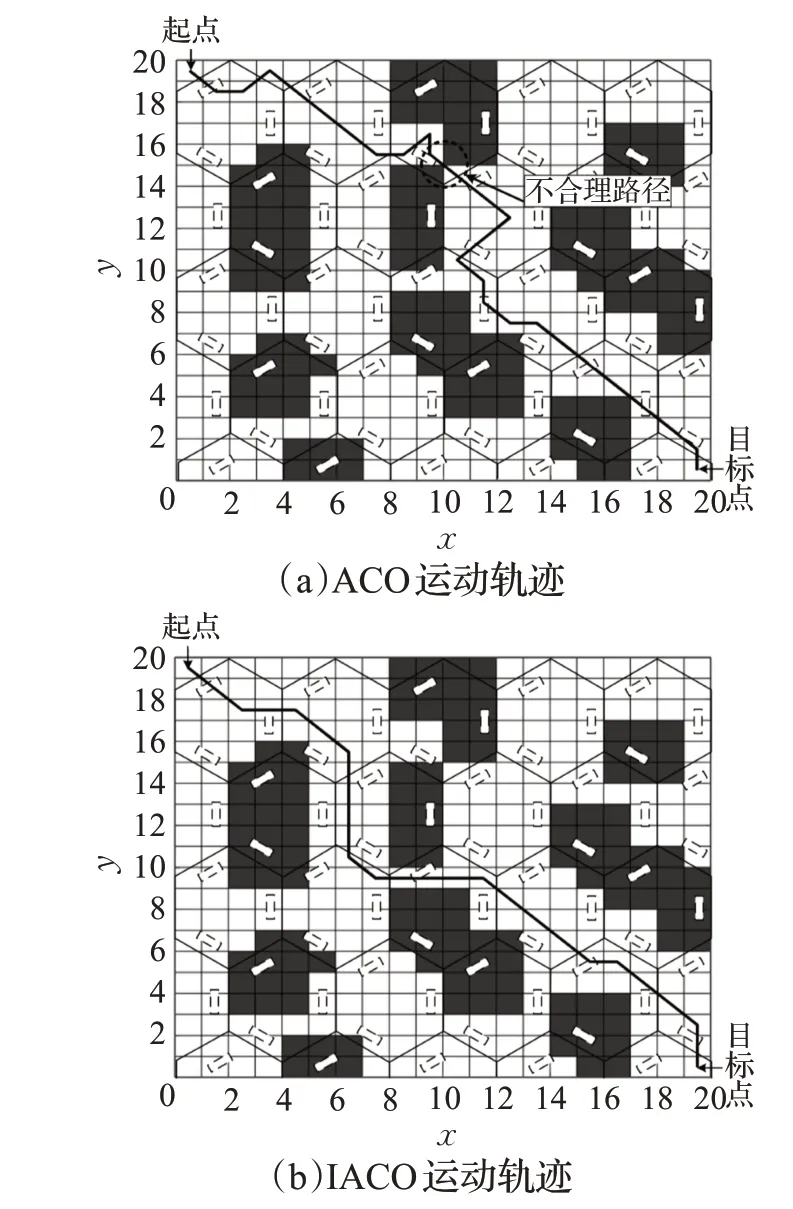


5.2 IAPF路径规划结果


5.3 IACSPF路径规划结果


6 结束语
