好奇心蒸馏双Q网络移动机器人路径规划方法
2023-10-10顾琦然
张 凤,顾琦然,袁 帅
沈阳建筑大学 电气与控制工程学院,沈阳 110168
路径规划是移动机器人的自主导航中十分关键的技术之一。为实现对移动机器人的运动轨迹进行有效的控制,使其能够顺利地通过各种障碍到达目的地,通常需要使用路径规划算法来保证获得最优路径。传统的路径规划方法过于依赖环境模型。而在深度强化学习中,深度学习能够对高维信息进行有效的处理,从而使机器人能够与周围的环境进行持续的互动;在马尔可夫决策过程的基础上,强化学习能够在复杂的环境中,实现移动机器人的连续决策来规划出实时路径。深度强化学习已成为工业机器人和室内移动机器人的路径规划方案之一[1],其最初用于游戏仿真领域中,Deep-Mind团队在2013年首次提出DQN(deep Q-network)模型[2]。当前,DQN 算法已成为路径规划的主要算法之一,可是传统的DQN算法存在着奖励稀疏、样本利用率低且过估计等问题。且针对这些问题,国内外许多学者进行了大量的研究。
对于奖励稀疏问题,文献[3]提出了一种基于DQN的路径规划算法,在此基础上对实际目标进行采样,加速训练,并在一定程度上解决了奖励稀缺性问题。文献[4]根据人的喜好来学习奖励函数,通过不使用奖励功能,而是通过选择路径来获得人类的喜好。文献[5]采用虚拟计数方法,通过信息增益,将状态频率转换为虚拟计数,并将其作为附加的内部奖励。
文献[6-12]分别通过RSV-DuDQN、二次主动采样方法、NDQN、LSTM、重采样优选机制、输入深度图像等对DQN算法进行改进,使DQN的性能得到了一定的改善,同时也解决了DQN的低采样率问题。
对于DQN 过估计问题,许多学者也提出了不同的解决办法。文献[13]提出一种DTDDQN算法,通过融合DDQN 与平均DQN 进行参数训练,使机器人在选择动作时不会过估计。文献[14]在DQN算法基础上与Sarsa算法进行融合,用于减少过估计对DQN 产生的不良影响。文献[15]提出一种EN-DRQN 算法,使得机器人可以发现许多新颖状态,并作出合理的决策。文献[16]提出使用重放缓冲器存储网络输出以改进DQN 算法,使机器人驱动功率提升。文献[17]在DQN 中引入修正函数来改善评估功能,使状态-动作值的最优与非最优的差异增大,来解决过估计问题。文献[18]提出了一种分散的传感器级避碰策略,能够为大型机器人系统找到有效的、无碰撞的路径。文献[19]提出在Gazebo仿真环境中对DQN 进行训练提升机器人的环境适应性,降低过估计影响。
上述方法,一定程度上提高了DQN算法的性能,但只是针对过估计、样本利用率低和稀疏奖励中的单一问题进行了有效改进,为了更有效地综合性解决此类问题,提出一种基于CDM-D3QN-PER 的端到端路径规划算法。在机器人感知端引入LSTM,通过“门”筛选关键信息解决点云信息的长序列数据问题;其次,使用PER对具有较高优先级的样本进行训练,解决样本质量的问题;接着融合CDM,增加机器人的内在好奇心,避免出现机器人因缺乏反馈而陷入困境的问题,提高环境探索率。最后,利用Gazebo平台对算法进行验证,并在两种不同的复杂仿真环境下,分别对DQN、DDQN、D3QN和CDM-D3QN-PER进行了比较。实验表明,CDM-D3QNPER算法的稳定性和到达目标点次数得到有效提升,该算法使移动机器人在与环境交互中可更高效地获取最优路径,在路经规划技术中具有一定的研究意义。
1 DQN及其改进算法
1.1 DQN
DQN 算法的两个创新点,即经验回放与设立单独的目标网络。DQN 针对Q-learning 做出一下改进:(1)DQN 中的数值函数是由深度CNN 逼近的。(2)在DQN中引入了一种基于经验回放的训练模型。(3)DQN独立地设定了用于分别处理时差算法TD误差的目标网络。Q-learning中的参数更新公式如式(1)所示:
其中,TD 目标r+γmaxa′Q( )s′,a′;θ在计算时用到了网络参数θ。
1.2 Double DQN
Double DQN 主要是解决DQN 过估计问题[20]。该方法的关键在于利用不需要的值函数,分别对TD 对象的行为进行选择以及对TD对象的行为评价。
在Q-learning中,TD对象的动作选择是在下一种状态下,被确定为最大的状态动作。动作评价是在选择下一种状态下的最佳动作,从而构建目标。DDQN使用不同的数值函数来选取和评价动作。其更新公式见式(2):
由上式可以看出,动作的选择采用θ网络,a*=arg maxaQ(St+1,a;θt)。动作评估采用θ′ ,1+γQ(St+1,a*;θ′t)。
1.3 Dueling DQN
Dueling DQN[21]把神经网络中Q价值的输出分成两部分,第一部分是状态价值V,这部分价值由状态直接决定和Action 无关。第二部分就是动作价值和状态价值的差值A,每一个Action都存在一个差值。这两部分构成倒数第二层的神经网络,节点数为Action数加1。然后最后一层的Q值就可以直接由V和A相加构成:
在实际操作中,需要减去一个平均值:
2 CDM-D3QN-PER算法
传统DQN算法在复杂环境中因为缺乏关键信息且奖励稀疏,规划任务很难成功,为了提高路径规划任务,提出了一种基于改进的双Q网络移动机器人路径规划方法——CDM-D3QN-PER算法。该算法在DDQN与Dueling DQN 融合的D3QN 模型的基础上,加入LSTM、CDM 和PER。CDM-D3QN-PER 算法模型如图1所示。
(1)移动机器人通过激光传感器搜集环境信息,并将当前时刻的状态信息送入可专用于处理雷达产生的长序列点云信息的LSTM中。
(2)双目相机将收集到的图像信息经过卷积神经网络处理,两者信息与Concat 函数结合,输入到D3QN 的输入端进行训练。
(3)获取到Q值和当前最优执行动作A,切换到下一时刻状态,将当前和下一刻状态信息输入到CDM 模型,计算出前向损失函数与预测损失函数。
(4)将当前和预测状态信息输入到CDM,获取反向损失函数,将两个损失函数整体优化并与预测损失函数对比,提高移动机器人环境探索效率,获取更多奖励值。不断重复进行以上过程,累积奖励值最大化,直至得到最优动作值函数Q对应的最优动作。
CDM-D3QN-PER算法具体流程如下所示:
2.1 机器人内在奖励获取方法——CDM
CDM-D3QN-PER算法中采用内在好奇心模块(ⅠCM)和随即网络蒸馏(RND)结合的随即网络蒸馏(CDM)算法获取内在奖励值。算法模型如图2所示。
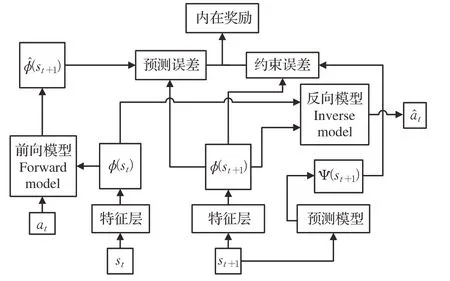
图2 CDM模型Fig.2 CDM model
ⅠCM 模型通过对前时间状态信息st和下一时间状态信息st+1进行特征提取计算出前向损失函数LF。输入当前动作at和预测动作ât,计算出反向损失函数LI。RND模型通过输入下一时间状态信息st+1计算出预测损失函数LP。
二者结合后的CDM 算法既保留了ⅠCM 把无用信息过滤掉的优势,确定特征提取后的信息都是有用的信息并保持探索,同时兼顾了RND 判断当前状态是否已经探索过。
其中前向模型(forward model)利用L2范数作为损失函数:
反向模型(inverse model)的损失函数为:
预测模型(predict model)的损失函数可表示为:
最后,机器人的学习目的是:
在D3QN算法中添加改进后的内在好奇心机制,将激光雷达采集的状态信息st作为CDM 模型的输入数据,在训练时不断优化网络参数,通过好奇心驱动机器人在路径规划任务中主动探索未知状态。
2.2 机器人点云信息处理方法——LSTM
激光雷达能够适应不同的光照环境,长短时记忆网络(LSTM)利用点云数据处理激光雷达采集到的环境与机器人状态数据,以解决长序列训练中的梯度消失、爆炸等问题。在路径规划中,收集到的数据经过该网络处理后得到统一的障碍物状态与机器人自身状态输入到D3QN网络中,再次经过全连接层处理后输出的便是用于选取最优动作的动作值函数Q,LSTM 的结构模型如图3所示。

图3 LSTM模型Fig.3 LSTM model
LSTM通过三个“门”机制完成信息的去留:
(1)首先,确定细胞状态丢弃的信息由一个叫“遗忘之门”的sigmoid 单元进行处理。在0 到1 之间,通过观察ht-1和xt信息,可以输出向量的保存还是放弃。
(2)利用ht-1和xt通过输入门的操作来决定更新信息。通过输入门得到新的机器人状态信息。
(3)在更新状态之后,要根据输入的和来判断输出的状态,通过输出端的sigmoid层获得一个判定条件,再通过tanh层获得-1的矢量,再用输出端获得的判定条件乘以这个矢量。
各单元门的工作原理公式如式(9)~(13)所示:
2.3 机器人样本处理方法——PER
在路径规划中,DQN 的取样方法采用了在经验回放中均匀取样,这种方法并不高效,对于机器人而言,由于这些数据的偏重性不同,针对该问题使用优先经验回放(PER)。该算法是指在均匀取样中,给有较高学习效率的样品以较大的取样加权。定义采样的概率为:
其中,Pα j对于第j个传输样本的优先权,α被用来调整优先度(当α取零时化成均匀取样),下面两种方式的不同是优先权的定义不同:
其中,δi为DQN的TD-error,ϵ用于防止概率为0。
PER 将当前状态信息、下一个状态信息、动作值等环境交互信息通过存储到记忆回放单元中,并对其中的样本以概率P进行优先级排序。
当记忆回放单元里的样本被储存到一定容量时,通过提取其中部分概率P高的样本,将样本中的当前状态信息输入到Q网络中,以获取当前状态信息的Q值。
3 实验结果与分析
3.1 仿真实验环境
由于深度强化学习的训练要求有海量的数据支持,而且在实际操作中很可能会破坏硬件设备,所以大部分的训练都是在仿真环境中进行。为了减少虚拟和真实场景中机器人可视测量的差异,即将激光测距技术应用于实验环境中。
实验环境为CPU服务器,TensorFlow框架,Python3.6,Gazebo7.0,采用Jackal 四轮机器人在Gazebo 搭建仿真环境中进行训练,其机器人带有激光测距技术。Jackal四轮机器人通过对运动中的实时定位进行分析,并对其与障碍物及目标点的距离进行分析,将激光传感器收集到相对自己坐标的坐标数据作为输入,输出连续的转向指令,通过激光测距传感器来实现探索最优路径。
在实验中,先把移动机器人的前向速度设置为:3 m/s,角速度为:0.03 rad/s,其余速度为:0.05 m/s。再构建有障碍和无障碍的室内环境进行训练,来检验DQN、DDQN、D3QN和CDM-D3QN-PER的算法性能。
如图4、5 所示,仿真环境1 是四面围墙都是完全封闭的,可以让机器人在这里接受训练,从而达到躲避围墙和抵达目的地的能力。仿真环境2是加入了5个正方体障碍物,分别是4个有规则和1个无规则,进一步提高了机器人的路径规划难度,并使其具备了规避静止障碍的能力,从而可以进一步验证算法的稳定性。

图4 仿真环境1Fig.4 Simulation environment 1

图5 仿真环境2Fig.5 Simulation environment 2
表1 为CDM-D3QN-PER 参数设置。在这里,探索因子ε起初值为1,ε∈(0.1,1),跟随机器人的迭代数增大呈线性下降趋势。经网络中的参数更新是基于均方根的随机梯度递减算法,根据每个缓存器的优先回放机制,从缓冲区中抽取最小比特尺寸为32 的采样更新网络。为达到路径规划的目的,将运动进行离散化,其基础运动包括:向前、向左转、向右转、左转弯、右转弯。在基础动作上修改不同速度值,使其增加到11 个离散的可执行动作,动作名称与速度值分别为A1(1,-1)、A2(1,-0.5)、A3(1,0)、A4(1,0.5)、A5(1,1)、A6(0.5,-1)、A7(0.5,0)、A8(0.5,1)、A9(0,-1)、A10(0,0)、A11(0,1)。

表1 仿真参数设置Table 1 Simulation parameters setting
奖赏值设置如式(17)所示:
在奖励设定中,奖励设定包含正、负两个奖励,以1为单位的红色圆筒为目标点,作用距离为0.8 m,移动机器人以影响距离阈值检测到目标位置,获得+20 正奖励,持续训练,直到超过时间或者冲撞,才能继续进行下一轮;如果机器人在最小的影响范围内与障碍物发生碰撞,则获得负值-20,本次训练结束,继续进行下一轮,完成指定的训练次数结束。训练次数是600回合。
3.2 实验结果对比分析
(1)无障碍环境仿真分析
DQN、DDQN、D3QN 和CDM-D3QN-PER 这4 种算法的奖励值随训练步数的变化趋势如图6所示,可以明显验证出CDM-D3QN-PER 算法的奖励得分更加稳定,在300回合逐渐稳定收敛。D3QN在410回合开始稳定收敛。可DQN、DDQN 算法波动性较大,尤其是DQN几乎完全波动,且两者奖励值均未出现稳定收敛。

图6 无障碍仿真环境累积奖励值Fig.6 Accumulated reward value for empty simulation environment
由表2可知,CDM-D3QN-PER算法在301~600回合中,平均奖励值稳定达到了30左右,且均为正数并稳定变化,在401~500 回合达到最大平均值30.82,其收敛效果远远超过其他3种算法。D3QN在401回合后平均奖励值才刚刚稳定在30左右,并在401~500回合达到最大平均奖励值29.82。DDQN 在201~300 回合达到最大平均奖励值15.60,且最终平均奖励值为负数。DQN 平均奖励值均为负数,在101~200 回合达到最大平均奖励值-5.59。

表2 无障碍环境的平均奖励值Table 2 Average reward value of empty environment
以上结果表明,CDM-D3QN-PER 算法可以在较少的回合数中完成对移动机器人的训练,并获得较高的平均奖励值,在该算法下移动机器人可以更好地与无障碍环境进行交互。
(2)有障碍环境仿真分析
从图7可以看出,除了CDM-D3QN-PER算法在350回合左右开始稳定收敛并已经完全掌握躲避障碍物的能力,并且可以成功到达指定目标点,获得相应正向奖励+20,其奖励值稳定在20 到40 以内。D3QN 在450 回合刚刚开始收敛,其余两种算法的奖励值均一直在正负值波动。

图7 有障碍仿真环境累积奖励值Fig.7 Cumulative reward value of obstacle simulation environment
表3 表明,DQN 算法的平均奖励值均为负值,说明移动机器人几乎无法到达指定目标点获取最优路径。DDQN算法除了在前100回合获得短暂的正值,且为最高平均奖励值5.60。D3QN 在101~200 回合中为负值1.19,其余皆为正值,并在401~500 回合中获得最高平均奖励值11.39,虽然与DQN、DDQN 相比训练效果有提升,但是仍然会产生碰撞。CDM-D3QN-PER 算法虽然因为环境增加了障碍物训练效果略微有些影响,但平均奖励值全为正值,最高平均奖励值为26.01。而DQN 和DDQN 算法的总平均奖励值皆为负数,这表示移动机器人训练效果欠佳,不适合复杂度较高的有障碍环境,并且D3QN 的训练效果也远不如CDM-D3QNPER稳定。
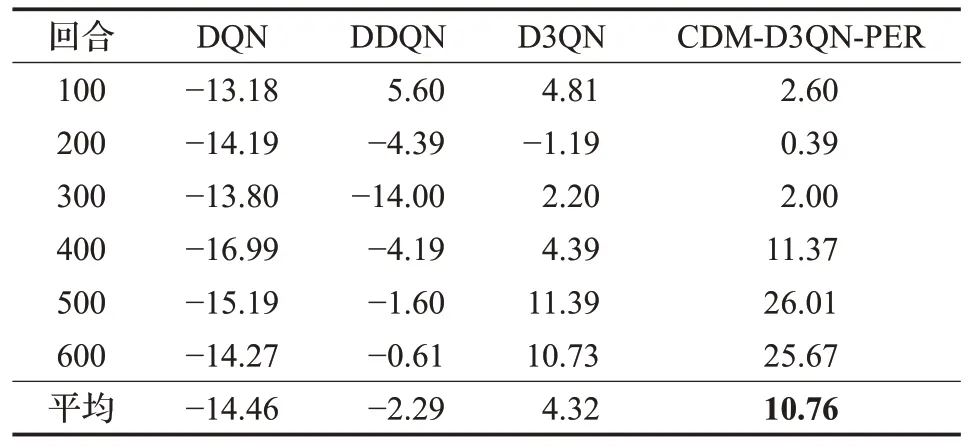
表3 有障碍环境的平均奖励值Table 3 Average reward value of obstacle environment
以上结果表明,CDM-D3QN-PER算法可以在较少的迭代次数下达成对移动机器人在有障碍仿真环境的训练效果,并获得较高的平均奖励值,获得最优路径。
移动机器人训练时,获取的正奖励值越多,说明机器人的动作策略越准确,在路径规划过程中,越容易绕开障碍物到达指定的目标点,最后得到的路径也是越接近最优的。
以成功率P(如式(18)所示),即移动机器人到达指定位置这一指标分析,CDM-D3QN-PER 比其他3 种算法有明显提高,CDM-D3QN-PER 在无障碍环境下600 回合中,有501 次到达了目标点,是DQN 算法到达次数的2.84 倍;在有障碍环境下,600 回合中,有428 次到达了目标点,是DQN算法到达次数的2.80倍。
在所有的600 回合中,Ng代表了成功完成任务的回合数,N代表了训练中的全部回合。
4 结束语
本文在传统DQN 算法的基础上,提出了基于CDM-D3QN-PER 的路径规划方法。首先,该方法以D3QN 模型为基础,使Q 值函数的估计更加准确。其次,在输入端将多传感器信息输入到LSTM和CNN中,使环境信息得到更有效的处理。然后,PER 算法的利用给重要的样本设置了优先级,提高了样本的利用率和网络收敛的速度。最后,融入CDM 算法增加了机器人的内在奖励值,提高了对环境的探索率。实验结果表明,CDM-D3QN-PER 算法的收敛性远优于其余三种算法,在移动机器人路径规划中具有更好的自适应能力和稳定性。
