机器人导航的路径规划算法研究综述
2023-10-10朱发证
崔 炜,朱发证
长春理工大学 电子信息工程学院,长春 130022
机器人自主导航一般分为感知、定位、路径规划与控制,而路径规划作为机器人导航的关键技术也成为了当下的研究热点。路径规划旨在通过规划算法在配置空间中找到从初始位置到目标位置的可行路径,而不会与任何障碍物发生碰撞[1]。现如今已在工业机器人[2]、仿生机器人[3]、无人车[4]、无人机[5]等领域得到了广泛应用。良好的路径规划算法可以快速规划出最优路径,提高运行效率,减少机器人的磨损[6]。
路径规划算法有多种分类方式,按照是否具有环境信息的先验知识分为已知环境下的全局路径规划算法和未知环境下的局部路径规划算法[7]。全局规划是一种静态规划,主要为局部路径规划提供导向和约束,局部规划是一种动态规划,用于未知环境中的实时避障。不过这种分类方法仅从实际应用的角度出发,难以清晰表述算法间的区别与联系。
本文系统总结了机器人的路径规划算法,将现有的算法划分为基于图搜索、基于仿生、基于势场、基于速度空间和基于采样的规划算法。由于基于采样的算法一般通过碰撞检测获得可行轨迹的节点信息避免了显式构造配置空间提高了规划效率,有效避免了维度灾难,日益成为解决路径规划问题最流行的算法,因此本文简述基于图搜索、基于仿生、基于势场和基于速度空间的路径规划算法,而重点分析基于采样的路径规划算法并将其分为单查询算法和多查询算法,即快速扩展树类和概率路线图类。
1 基于图搜索的算法
基于图搜索的算法是遍历的确定性搜索方法,通常用于维度较低的空间,如二维空间,一般将地图离散成栅格图后利用搜索策略以尽可能小的代价找到路径,但是这类算法的性能取决于所选的地图分辨率大小。如果分辨率太小,则可能找不到合适的路径,如果分辨率太大,则可能需要耗费很长时间[8]。并且随着地图规模的增大,它们的搜索性能也会越来越差。该类算法主要用于在静态地图中求解最短路径,其搜索过程直观,是解决环境已知时的全局路径搜索问题的算法[9]。
(1)Dijkstra算法[10]是一种广度优先搜索算法(breadthfirst search,BFS),虽然能够获得到达终点最短的路径,但是运算量大,规划效率很低。
(2)A*算法由Hart等[11]于1968年发表,是一种常用的路径查找和图形遍历算法。它融合了Dijkstra算法和启发函数,搜索权值函数如式(1):
其中,g(n)是节点n距离起点的代价,h(n)是节点n到达终点的预估代价,即启发函数。
A*算法不仅利用启发函数提高了路径搜索的效率,还能在给定相同信息的情况下,保证不会比任何其他最优算法扩展更多的状态(即它是最有效的)。但是实时性差,随着地图的增大或维数的增加,规划时间也成倍数地增长。
(3)A*的各种改进算法如图1所示,其中,Li等[12]提出的一种改进的双向A*(bidirectional A*)算法在A*算法的基础上引入了双向交替搜索策略,即分别从起点和终点开始搜索,直到路径相遇,提高了算法的搜索效率。Likhachev等[13]提出的ARA*(anytime repairing A*)算法是A*算法的anytime变体,先快速规划出一条初始路径,然后在时间允许的范围内不断优化这条路径。Stentz等[14]提出的D*算法是A*算法的动态变体,即从终点开始搜索路径,当出现新的障碍物时就可以将已有的代价值作为启发函数重新进行规划,所以可用于动态环境中的路径规划。Koenig 等[15]提出的LPA*(lifelong planning A*)算法是A*算法的增量变体,当环境发生变化后就可以利用先前存储的信息进行增量式搜索,虽然可以应用于动态环境,但是不适用于起点和终点变化的情况。如果机器人前进过程中某些节点发生变化,则可以使用Koenig等[16]提出的D* Lite算法,该算法在LPA*算法的增量搜索的基础上添加了反向搜索,不过当地图变动过大时可能耗时更长。Likhachev等[17]提出的AD*(anytime dynamic A*)算法也称Anytime D*算法,结合了ARA*算法和D*Lite算法的优点,适用于动态环境中的路径重规划,并且追求有限时间内的次优路径。上述改进算法的主要目的是缩短A*的规划时间,不过规划出的路径转折点仍较多,需要进行平滑处理。

图1 A*的各种改进算法Fig.1 Various improved algorithms of A*
基于图搜索的算法搜索过程简单直接,多用于机器人的全局路径规划,但是当地图精度高时规划路径所需的计算量大且转折点较多。另外,基于图搜索的算法被不少学者用于计算初始路径或利用启发式思想优化其他算法。
2 基于仿生的算法
基于仿生的算法是模拟自然界中生物进化或群体行为的一种路径规划方法,算法原理容易理解,对环境具有良好的适用性,多用于全局的路径规划。
(1)遗传算法(genetic algorithm,GA)于1962 年被Holland[18]提出,它主要通过选择、交叉、变异来模拟生物进化进行搜索,有利于全局搜索。但是其收敛速度慢,且属于随机类算法,不能稳定地得到最优解。徐力等[19]通过加入插入算子与删除算子对交叉和变异概率进行了自适应调整。Pehlivanoglu等[20]提出了初始种群的增强方法来加速算法的收敛过程。Hao等[21]提出了一种基于碰撞检测的自适应遗传算法解决了路径质量低、收敛所需迭代次数多的问题。
(2)蚁群(ant colony optimization,ACO)算法于1991年被Dorigo等[22]提出,它是模拟蚁群在自然界中寻找食物的行为特征而形成的一种正反馈机制算法,其关键为状态转移和信息素更新。Luo等[23]提出了一种通过差异化分配初始信息素来避免早期盲目搜索的方法,根据当前最优解和迭代次数计算状态转移概率,并引入最优解和最差解来改进全局信息素的更新。Miao 等[24]在蚁群算法的转移概率中引入了角度引导因子和障碍物排除因子来缩短规划时间。Liu等[25]提出了一种基于概率的随机游走策略,通过交替使用高斯分布和柯西分布来生成随机游走的步长,而不是仅使用高斯分布来构造新的解。
(3)粒子群算法(particle swarm optimization,PSO)于1995年被Kennedy等[26]提出,它是模拟鸟群等种群觅食生存行为提出的一种群优化算法,每个个体只有位置和速度两种属性。其核心思想是利用集群中的信息共享使群体从无序到有序[27]。Phung 等[5]提出了一种通过球向量优化的粒子群算法,通过制定成本函数将路径规划转换为优化问题,重点关注路径的安全性和可行性。Yu等[28]通过融合模拟退火算法改进了PSO算法的更新策略,提高了群体的多样性,避免陷入局部最优解。Fernandes 等[29]提出了一种使种群具有多峰值的算法以有效避免局部极小值。
(4)萤火虫算法(firefly algorithm,FA)于2008 年被Yang[30]提出,它是一种基于萤火虫闪光特征的随机的群体智能算法,吸引行为、光强编码和距离依赖性使FA能够有效地处理非线性、多峰优化等问题[31-32]。Patle 等[33]进行了FA在不确定环境中移动机器人导航的应用和实现,减少了计算量,避免了萤火虫的随机移动。Xu等[34]研究了用于移动机器人路径规划的优化FA,优化后的高性能算法可以提高移动机器人在路径规划中的计算能力和响应速度。Li等[35]提出了一种基于FA的最优路径规划方法,用于自适应种群大小。Zhang 等[36]提出了一种新的基于GA和FA的混合算法,将新的混合算法应用于路径规划可以提高机器人在路径规划中的反应能力和计算能力。
(5)灰狼优化(grey wolf optimizer,GWO)算法于2014年被Mirjalili等[37]提出。该算法受到了灰狼捕食猎物活动的启发,在本质上模拟了灰狼的领导层次和狩猎机制,具有收敛快、参数少、易实现等特点。Mirjalili等[38]首次提出了一种多目标灰狼优化算法(MOGWO),用于多目标问题的优化。Gupta等[39]提出了一种基于随机移动的改进RW-GWO 算法来提高灰狼搜索能力。Nadimi-Shahraki 等[40]提出了一种改进的灰狼优化算法(Ⅰ-GWO)以解决种群多样性不足、早熟收敛等问题。
除了上述算法,国内外学者在机器人路径规划中还采用了一些其他优化算法,如海洋捕食者算法[41]、搜索与救援优化算法[42]。海洋捕食者算法通过模拟海洋生物的捕食行为,利用捕食算子和消除个体聚集算子实现规划目的。不过存在前期收敛慢、收敛精度低等缺陷。张贝等[43]提出了融合趋向最优的反向学习策略和信息共享策略的海洋捕食者算法,有效避免了算法陷入局部最优,加快了算法的前期搜索速度。搜索与救援优化算法通过模拟人类的搜救行为,利用个人阶段和社会阶段两个算子进行规划。该算法简单、不易陷入局部最优,但是收敛慢且难以自适应地调整搜索区域。周文娟等[44]提出了一种基于强化学习改进的搜索与救援优化算法,通过训练强化学习模型使算法具有自适应选择能力。Zhang等[45]提出了一种启发式交叉搜索和救援优化算法,保持群体多样性的同时提高了收敛速度。
基于仿生的算法对环境的适应性强,常用于全局规划,不过易出现迭代次数多、收敛速度慢、路径质量低等问题。研究新算法或融合算法可以获得更好的规划性能,如猎豹优化算法[46]、鲸鱼优化算法[47-48]、模拟退火算法与自适应大规模邻域搜索算法相融合[49]、遗传算法与萤火虫算法相融合[36]。
3 基于势场的算法
基于势场的算法通过跟踪由引力部分和斥力部分组成的势场的最陡下降来找到可行路径,合力的方向表示期望的运动方向,大小表示期望的速度[50]。其中,引力由终点产生,斥力由障碍物产生,机器人的受力如图2所示。该算法结构简单,计算负担较小,常用于在线规划进行实时避障。

图2 基于势场的算法示意图Fig.2 Schematic diagram of potential field-based algorithm
人工势场法(artificial potential fifield approach,APF)[51]结构简单,易于计算,不过当引力与斥力相差较大、合力为零或机器人在狭窄通道时易存在目标点不可达和局部极值两个主要问题。另外,当机器人周围存在多个障碍物时,可能会导致加速度振荡,从而出现高能耗问题[52]。为了避免出现人工势场法的局部极小值问题,Tian等[53]基于已知目标位置和最小安全距离构造了一个内部无障碍物的虚拟导引管道(virtual guiding pipeline,VGP)来构造导向势场,Sang 等[54]通过切换子目标点来改进算法,Souza 等[55]引入了一个三维涡流场进一步避免震荡问题,Duhe等[52]也提出了四种排斥场的替代公式来减少由障碍物造成的加速度震荡现象。
4 基于速度空间的算法
基于速度空间的算法核心思想借鉴了预测控制的相关原理,是一种移动机器人在线避碰策略。该算法不仅考虑了机器人本身的物理约束,还通过考虑环境约束和当前速度为机器人规划一条合适的路径,并在出现动态障碍物时快速采取相应的避障行动[56]。
动态窗口法(dynamic window approach,DWA)[57]首先根据机器人的运动学模型和当前速度获得速度的采样窗口,然后通过评估函数评估在窗口内生成的所有轨迹,最终找到下一时刻的最佳速度。其中评价函数通常考虑障碍物距离、速度和路径角度三个因素。该方法主要用于移动机器人的自主避障,能够用于计算机器人达到目标所需的最大无碰撞速度[58]。DWA虽然考虑了多种约束,但是前瞻性不足且易出现局部极值。起初DWA 主要用于静态障碍物环境[57,59],Ogren 等[59]利用李雅普诺夫函数框架提出了一种易于处理且收敛的DWA。而当障碍物动态移动时,DWA 的性能便会下降。为了克服此限制,已经开展了大量在动态障碍环境中进行避障的研究[60]。Molinos 等[61]提出了采用两级窗口的DW4DO(dynamic window for dynamic obstacles)算法以解决算法的迭代速度很高或机器人的加速度很低时出现的局部窗口很小的问题。而提出的另一种DW4DOT(dynamic window for dynamic obstacles tree)算法提高了规划路径的优化程度,减少了评估的路径数量,不过同时增加了计算成本。Lee等[60]提出了FDEDWA(finite distribution estimation-based dynamic window approach),通过FMF(finite memory filtering)估计障碍物的总体分布,并预测未来的动态障碍物分布,提高了机器人轨迹的最优性,同时保持了实时性能,不过还没有扩展到三维空间。Chang 等[62]通过Q-learning 自适应地学习所提出的DWA 的参数,并获得一个经过训练的Agent以适应未知环境。
5 基于采样的算法
基于采样的算法不使用环境的显式表示,一般通过碰撞检测获得可行轨迹的节点信息。然后将空间中的无碰撞节点连接起来形成一个可行轨迹图(路线图)。最后,在路线图中获得从起点到终点的可行路径[63]。基于采样的算法通过采样避免了显式构造配置空间,建模简单,成为近年来解决高维规划问题最流行的算法,主要分为单查询算法和多查询算法。基于采样的算法的节点扩展步骤如图3所示。
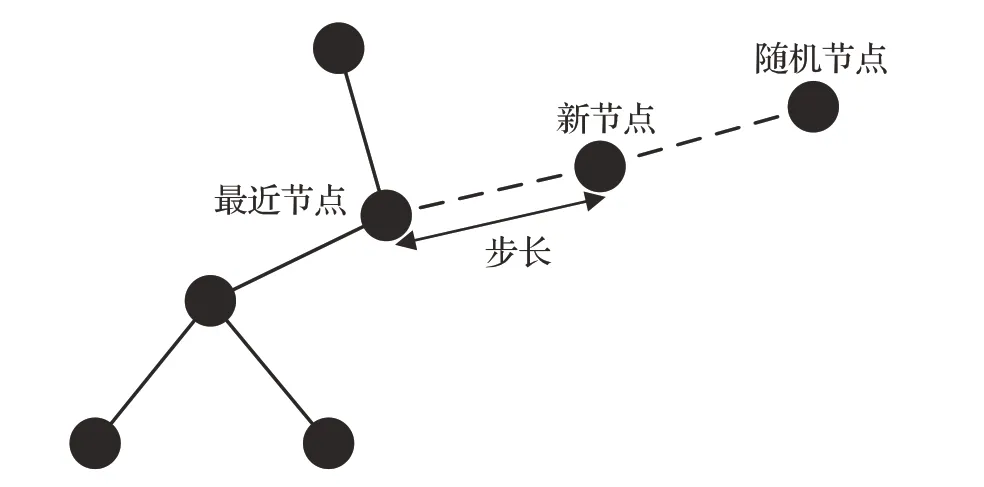
图3 基于采样的算法节点扩展示意图Fig.3 Schematic diagram of sampling-based algorithm node expansion
5.1 单查询算法
单查询算法通常解决只有一对起点和终点的路径规划问题,常用的例子包括RRT算法[64]与它的渐进最优版本RRT*算法[65]、FMT*算法[66]和BⅠT*算法[8,67]等。
RRT(rapidly exploring random tree)算法[64]从起点开始生长一棵树,以增量方式近似状态空间,如果在达到最大迭代次数时未找到从起点到终点的可行路径,则该规划被视为失败。而且采取随机顺序搜索策略,使它的搜索效率很低。Wang等[68]提出了一种在动态环境中的EB-RRT(elastic band-based rapidly exploring random tree)算法,将EB(elastic band)方法与基于时间的RRT树相结合,在优化当前轨迹的同时实现实时运动规划。不过当动态障碍物的运动方向突然反转时,该算法难以及时避免碰撞。Chi 等[69]提出了一种基于广义Voronoi图的启发式路径规划算法,用于生成启发式路径,指导采样过程,进一步提高运动规划效率。然而它只讨论了在具有广泛可行区域的较不复杂环境中的性能,对于更加复杂的情况具有不确定性。
RRT*算法[65]扩展了RRT 算法,当添加新节点时,RRT*算法通过重新选择父节点以确保新节点对应的路径具有局部最小值,并且在添加新节点后重新布线以减小路径代价。该算法在样本数接近无穷大时以概率1收敛到最优,不过其状态空间的全局搜索仍然是随机的,且由于收敛速度慢和初始路径代价高,使其规划效率较低。曹凯等[70]通过APF引导RRT*解决了在多障碍物等复杂环境中的收敛慢、采样点多的问题。Arslan等[71]提出的RRT#算法使用启发式在快速搜索随机树逐步构建的图中查找和更新树。Otte 等[72]提出的RRTX算法将重新布线扩展到了动态环境,在导航期间使用相同的搜索树,当检测到状态空间的变化时不断对其进行优化和修复。不过与RRT*和RRT#一样,它不会对图本身的构造进行排序。Liao 等[73]提出了F-RRT*算法,通过为随机点创建靠近障碍物的父节点(不是在现有顶点中选择)来优化路径成本,生成的初始路径比RRT*更好,收敛速度更快。
RRT-Connect 算法[74]分别从起点和终点开始生长树,并使它们的生长既偏向于未探索的空间,又偏向于彼此,会快速得到一个初始路径,但未探索空间的搜索仍然是由增量采样随机排序的,且它不是一个渐进最优的算法,无法改进初始路径。Wang 等[75]提出了一种基于RRT-Connect 搜索的高效路径规划算法,采取“双向到单向”策略,即当两棵树相遇时,后向树将作为一种启发式,引导前向树不断向目标状态生长,算法将切换到单向搜索模式。因此,避免了连接过程中的两点边值问题,大大加快了扩展过程,不过它只是将后向树用来启发前向树,所以搜索速度低于RRT-Connect算法。
Ⅰnformed RRT*算法[76]改变了传统算法的采样方式,在找到第一条路径之前与RRT*相同,而在找到第一条路径之后Ⅰnformed RRT*将超椭球启发式纳入RRT*,减少无用区域的采样,加快了收敛速度,同时保留了RRT*的概率完备性和渐进最优性。由于Ⅰnformed RRT*使用启发式将规划问题缩小到的是原始空间的子集,因此它本质上依赖于所找到的初始路径。Wang等[63]提出了一种基于目标偏向采样和启发式优化策略的TBⅠT*算法,该算法在寻找初始路径的搜索阶段采用“向日葵”区域和目标牵引区域组合的目标偏向采样策略,引导随机树向目标方向快速增长,从而减少冗余节点的生成,提高算法的搜索效率。搜索初始路径后,算法将依次选择路径中的三个节点,形成一个超椭球进行路径优化,减少了无用的计算,并提高了算法的收敛能力。不过由于它优化的是初始路径本身,因此对于一些存在狭窄通道的复杂场景可能规划不出最优路径。
FMT*(fast marching tree)算法[66]使用惰性碰撞检测来减少对障碍物碰撞检查的数量,使用行进法处理一组样本,搜索结果按成本排序,比RRT*算法的收敛速度更快[77]。其近似和搜索的分离使得搜索顺序与采样顺序无关,但很难选择合适的样本数量,当需要较低成本的路径时,必须增加样本数量再重新规划,并且在搜索结束之前,不会给出可行路径,如果没有找到合适的路径,搜索就必须重新开始。Salzman 等[78]提出的MPLB(motion planning using lower bounds)算法是FMT*算法的anytime变体,同时处理多个节点以有效计算所有节点的估计成本,并使用下限将RRT*的渐进最优放宽到了渐进近似最优,不过没有提出具体的方法来重用信息。Starek 等[79]提出的BFMT*(bidirectional fast marching tree)算法执行双向惰性搜索,当两棵树相交或某一节点在一棵树的开放集中而不在另一棵树的开放或未访问集中时终止搜索。并且该算法保留了概率完备性和渐进最优性。Reid等[80]提出的HBFMT*(hierarchical bidirectional fast marching tree)算法是一种分层双向快速行进树,将配置空间分解成多个子空间的层次结构,利用双向搜索快速找到一组通过这样的子空间的路径,这个初始路径用于生成一个有偏采样分布,然后探索所有空间找到一个路径。每个子空间由FMT*变体搜索,保留了FMT*的概率完备性和渐进最优性,不过其性能依赖最初采样的子空间和生成的分布。Xu等[81]提出的BBⅠ-FMT*(Batch-to-batch Ⅰnformed Fast Marching Tree)算法是一种anytime算法,利用批量采样的增量搜索和“懒惰”最优搜索快速找到初始路径后,再通过批量知情采样的增量搜索快速优化树并获得最优路径。随后,Xu 等[82]又提出的ⅠAFMT*(informed anytime fast marching tree)算法使用了一种平衡批量和单次采样、“非懒惰”和“懒惰”搜索优点的策略,即采用混合增量搜索和动态最优搜索。混合增量搜索构建了一个低成本的生成树,兼顾了批量采样搜索的效率和单次采样搜索的灵活性。动态最优搜索考虑了“非惰性”和“惰性”搜索之间的权衡,以快速改进所生成树并获得高质量的可行 路 径。Wang 等[1]提 出 的ⅠABFMT*(informed anytime bi-directional fast marching tree)算法是一种基于渐进最优采样的anytime算法,结合了BFMT*算法的双向搜索和ⅠAFMT*算法的anytime的优点。ⅠABFMT*算法首先通过双向“惰性”搜索较少数量的样本以有效地找到可行的初始路径,再通过知情采样将样本数加倍快速改进为最优。与ⅠAFMT*相比,ⅠABFMT*只搜索可以优化当前路径的区域,而不是整个知情集。Wu 等[83]提出的ST-FMT*(secure tunnel fast marching tree)算法由预处理和探索两部分组成,分别负责建立“安全通道”和优化路径,其中通过障碍物到初始路径的最小距离建立的“安全通道”有助于采样的集中。
任何时候,基于采样的规划都可以被视为在问题域中构造图并搜索的算法。一些算法同时进行这种构造和搜索(例如RRT*),而另一些算法则单独进行构造和搜索(例如FMT*),但与基于图搜索的算法一样,它们的性能始终取决于近似的准确性和搜索的质量[8]。
BⅠT*(batch informed tree)算法[8,67]使用RGG(random geometric graph)理论[84]来限制图的复杂性,以anytime的形式构建图并使用类似于LPA*算法[15,85]的方式进行搜索。anytime 允许BⅠT*无限期运行,直到找到合适的路径。有序搜索避免了不必要的计算量。增量搜索允许它通过重用以前的信息来有效地更新其不断增加的批次。Holston 等[86]提出的快速BⅠT*(fast-BⅠT*)算法通过仅按成本进行初始搜索,以降低初始最优性为代价来更快地找到初始路径。一旦找到一条可行路径,它将使用完整的启发式重新排序其队列,并重新处理所有节点。虽然保持了几乎确定的渐进最优性,但不必要地重复了以前的搜索工作。Strub等[87]提出的ABⅠT*(advanced batch informed tree)算法利用BⅠT*单个查询中搜索和近似的分离在基于anytime采样的近似上使用基于图形的高级搜索技术(膨胀和截断),以进一步提高规划性能。通过膨胀其启发式来加快初始解时间,类似于ARA*[13]算法,并通过截断其搜索来平衡探索和近似,类似于截断LPA*[85]算法。其中,膨胀会使搜索偏向目标,减少规划时间,截断有助于探索状态空间的区域。与BⅠT*使用的增量搜索相比,虽然实现了更快的路径规划,但是牺牲了分辨率的最佳性。Kyaw 等[88]针对存在不规则障碍物和狭窄通道的复杂环境,提出了可重构机器人的节能BⅠT*(energy-efficient BⅠT* for reconfigurable robots*,EBⅠTR*)算法,该算法将机器人执行器的机械功作为能量成本目标,把搜索重点放在贪婪的知情集上(BⅠT*直接在知情集上采样),在保持BⅠT*的概率完备性和渐进最优性的同时,生成高质量、节能的路径。Strub等[89-90]提出的AⅠT*(adaptively informed tree)算法是自适应启发式的快速渐进最优路径规划,建立在BⅠT*的基础上,使用非对称双向搜索来有效地估计和利用每个问题实例的精确启发式。正向搜索与BⅠT*算法中的搜索相同,不过使用计算成本更低的反向搜索提供的启发式。如图4(a)所示,BⅠT*采用欧氏距离估算启发式成本(虚线)会使其忽略中间的障碍物,而通过使用惰性反向搜索,AⅠT*能够提供更精确的启发式以适应这种场景,如图4(b)所示。另外,AⅠT*找到初始路径的速度至少与RRT connect 的速度一样快。Strub 等[90]提出的EⅠT*(effort informed tree)算法作为AⅠT*的一个扩展,能够用于优化计算成本较高或难以用可接受的先验成本启发式近似的目标,该算法的正向搜索利用反向搜索计算的额外的成本和努力启发式,即使没有可接收的启发式,这也会使它能快速的得到初始路径。
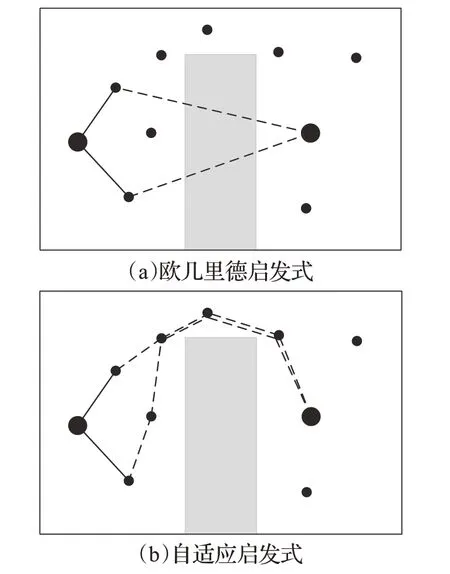
图4 欧几里德启发式与自适应启发式对比图Fig.4 Comparison diagram of Euclidean heuristic and adaptive heuristic
单查询算法能够得到连接一对起点和终点的可行路径,建模简单,可以有效解决高维规划问题。但是在固定场景中会造成重复性的规划,浪费计算资源。
5.2 多查询算法
许多环境的底层结构是静态的,往往会带来重复性的规划问题[91]。多查询规划算法旨在通过利用这种重复性构造一个路线图减少找到可行路径所需的计算时间来解决静态环境中的多个不同起点和终点的路径规划问题,常用的例子包括PRM 算法[92]与它的渐进最优版本PRM*算法[65]。
PRM(probabilistic roadmaps)算法[92]通过在预处理期间随机采样配置空间中的状态来构建离散化空间的路线图(保留自由空间中的样本,丢弃障碍空间中的样本)。它在预处理阶段会验证路线图中的所有边,然后使用此路线图将单个查询简化为路线图上的图搜索,从而缩短规划时间。如果环境事先不可用,则需要并行计算可重用信息以解决规划问题。而且若采样点数过少、邻域过小,则可能找不到解,若采样点数过多、邻域过大,则会更加耗时。Bohlin 等[93]提出的Lazy PRM 算法通过假设路线图中的所有边和顶点都是有效(无碰撞)地来减少近似阶段的成本,然后搜索以找到路径,接着对这个候选路径的顶点和边进行碰撞检查,如果包含碰撞,则会删除相应的顶点和边,并在更新的图上开始新的搜索。
PRM*、Lazy PRM*算法[94]扩展了PRM 和Lazy PRM 以获得几乎确定的渐进最优性,但是后续添加新样本时并不删除原有样本,使得路线图变得越来越大,会减慢后续的查询。Dobson等[95]提出的SPARS算法通过将先前找到的路径存储在稀疏图中来解决图的无限增长问题,不过稀疏图的构建在计算上是昂贵的,并且可能导致总体上的规划时间较慢。Lai 等[96]提出的RRdT*(rapidly-exploring random disjointed-tree*)算法继承了RRT*的概率完备性和渐进最优性,是一种增量式最优多查询规划算法,自适应地平衡了规划过程中的全局搜索和局部开发,通过使用多个“独立树”来探索空间以有效应对狭窄通道的情况,提高了传统算法的性能。Lai等[97]通过提议分布的贝叶斯学习改进了RRdT*算法,从过去观察到的结果中学习,而不仅仅是丢弃失败的样本,最大限度地提高了在狭窄通道内具有更高概率形成轨迹的区域进行采样的可能性。Hartmann 等[91]提出的EⅠRM*(effort informed roadmaps)算法将EⅠT*扩展到了多查询算法,通过将近似倒回到第一批样本来防止高分辨率图的复杂性对搜索性能产生负面影响,同时使用非对称双向搜索识别可能有助于解决单个规划的现有路径以减少计算量,能够快速找到一条初始可行路径,后续再优化到最优。
多查询算法通过利用已知的路线图进行快速规划,有效避免了出现重复性的规划问题,不过如何利用规划成功的路径信息构造路线图是该类算法的难题,并且与单查询算法一样搜索效率受采样点数量的影响大。
6 讨论
目前国内外学者对机器人的路径规划算法进行了应用研究,并取得了大量有价值的研究成果,具有代表性的算法如表1所示。
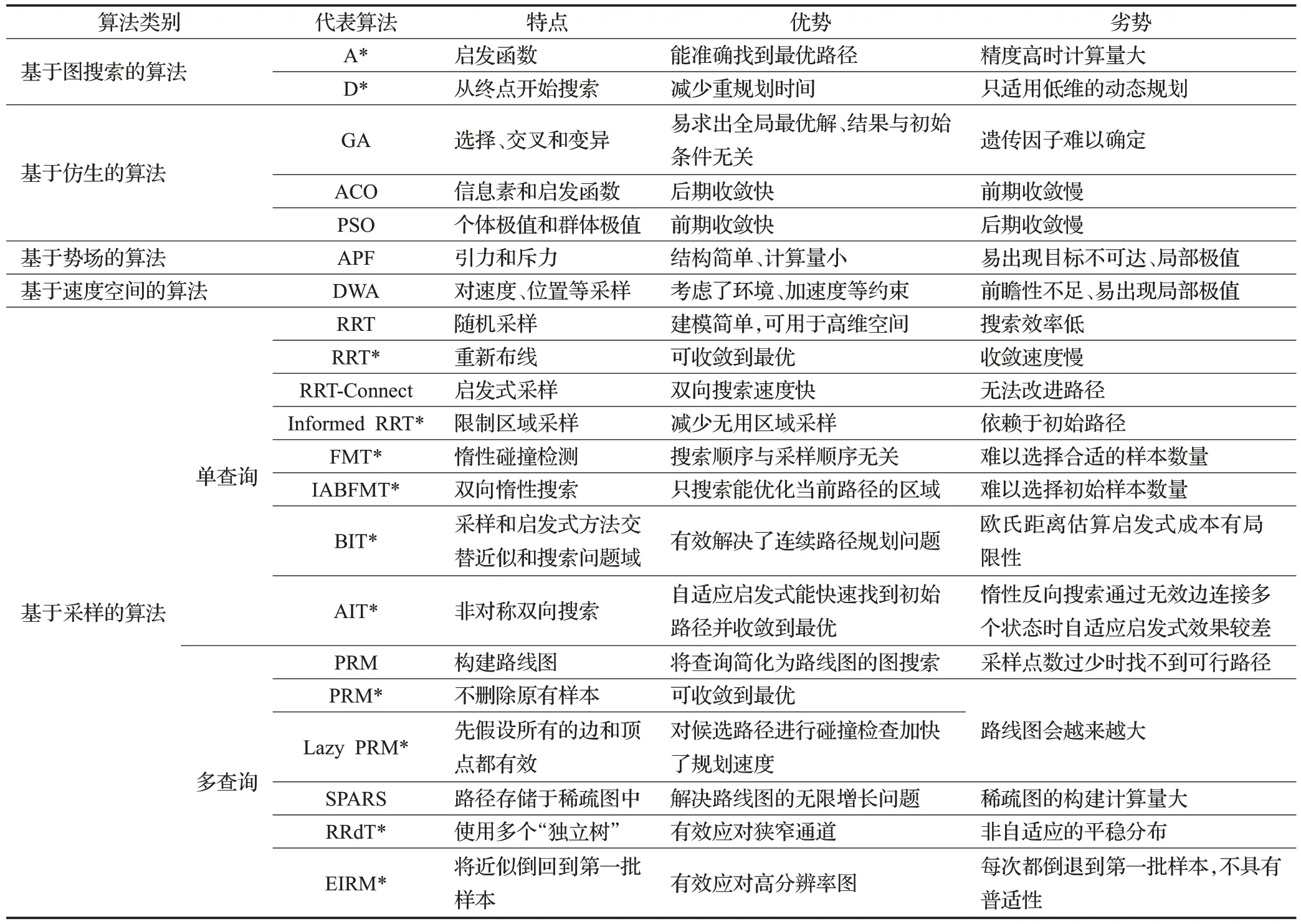
表1 路径规划代表算法汇总Table 1 Summary of representative algorithms for path planning
基于图搜索的算法的规划效率受限于其精度,精度越高,路径质量越好,但是所需的规划时间也越长,且难以找到一个合适的精度,多用于全局路径规划或为其他算法提供初始信息。基于仿生的算法对环境具有良好的适应性,国内外学者通过研究新优化算法或与其他算法相融合来提高实际应用效果。基于势场和基于速度空间的算法虽然简单、计算负担较小,但是易出现局部最优、震荡等问题,通常作为局部路径规划算法进行实时避障。基于采样的算法搜索能力强,不过也可能由于无序搜索或不准确的启发式而浪费大量的计算资源。另外,单查询规划算法中Ⅰnformed RRT*算法的限制区域采样、FMT*算法的惰性碰撞检测、BⅠT*算法的近似和搜索分离,以及AⅠT*算法的非对称双向搜索均有效提升了算法的规划性能。而针对一些场景的静态底层结构问题,多查询算法通过构造路线图来避免重复性的路径规划,减小了计算量。
7 结语
本文主要阐述了基于图搜索、基于仿生、基于势场、基于速度空间和基于采样的路径规划算法,从单查询算法和多查询算法等角度重点分析了基于采样的路径规划算法。从算法的发展现状和现实的需求来看,路径规划算法的下一步研究方向主要包括以下五个方面:
(1)狭窄通道环境中的路径规划
狭窄通道内有限的自由空间严重限制了算法的性能,如何在存在狭窄通道的复杂场景中进行快速的规划出一条可行路径已成为重难点,而基于采样的双向搜索已被证明有助于发现狭窄通道[80],因此未来应进一步研究在狭窄通道复杂环境中的双向路径规划算法。
(2)多机器人协同的路径规划
由于无人机集群协同、无人车编队协同等的现实需要,如何为多机器人规划出有序、安全、节能的路径显得尤为重要。传统上多采用粒子群等智能仿生算法,近年来,随着强化学习和深度学习显示出的良好的性能,将其应用于路径规划能使多机器人协同调度更灵活高效,所以基于强化学习和深度学习等方法进行多机器人协同的路径规划是重要的研究方向。
(3)多算法融合的路径规划
有的算法注重全局的最优性,导致实时避障时性能不佳,有的算法注重躲避障碍物时的快速性和安全性,却易造成局部极小值。单一的路径规划算法由于其局限性和片面性难以满足复杂环境下人们对速度、能耗、安全等的要求,因此结合多种算法优点的融合算法是实现机器人路径规划的发展趋势。
(4)高质量解的路径规划
算法规划出的路径质量可以根据长度、平滑度和安全距离来衡量,然而算法能否收敛到最优解通常是理论上关注的问题,实际应用需要的是高质量的路径,即代价低于给定阈值的路径。所以未来应进一步通过设定阈值函数、改变障碍物建模半径或发明轻量级方法来研究符合实际应用的高质量解的路径规划算法。
(5)自适应的路径规划
大部分路径规划算法针对的都是特定场景,当遇到超出预料场景的规划问题时,易出现规划速度慢甚至失败的情况,降低了机器人的安全性、实用性,因而通过数据、经验或其他方法进行不同场景下的自适应规划,是未来机器人路径规划的发展方向。
